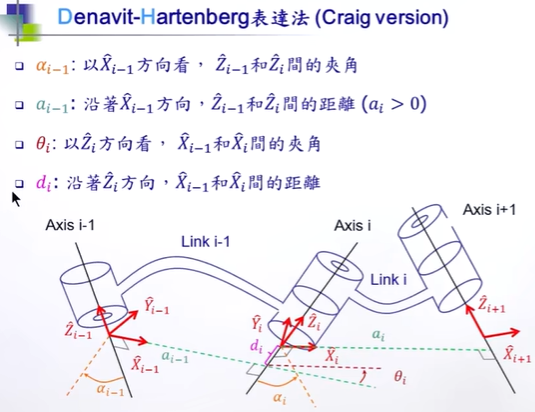
運動控制理論(4)——逆解

pw:世界坐標
P:最后一節點在最后一個坐標系下的局部坐標
在逆解中,Pw已知,P也已知,可以得到T,要由T得到θi,di (旋轉和伸長)
正算的例子:
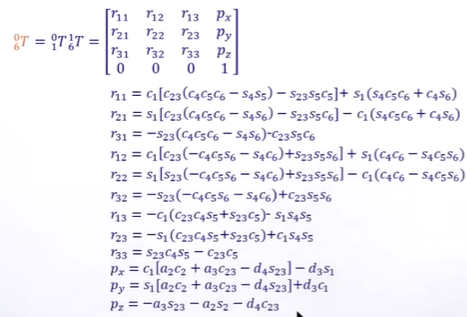
一般來說,正算的時候,不會用矩陣相乘的辦法,而是將每個元素單獨算,節省CPU開銷

3 個長度為1 + 3個相互垂直 = 6個限制條件
3*3矩陣 + 3*1向量 = 12條方程
6個未知數
獨立(線性無關)方程數 > 未知數,那么就是有多解了。

多解

求解方法:
一、解析法,分為:
(一)代數法 algebraic。直接在方程式上,做加減乘除,合并消去。(不就相當于手算了)
(二)幾何法 geometric。用最后的幾何,拆解成三角函數表示的方法。(是不是先算出手臂的各個向量,再反算角度???)
二、數值法。用電腦解方程。
* 目前大多數手臂設計成具有解析解。
* 解析解是real time控制中最快的。

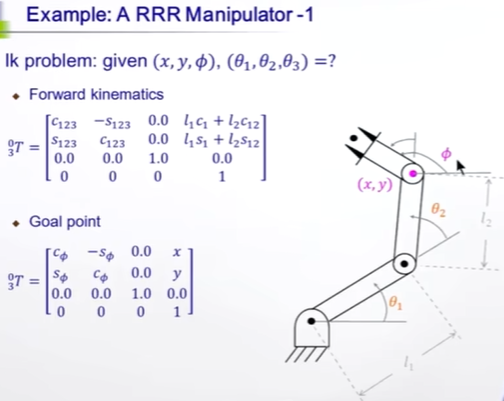
已知Φ,x,y
x,y,是世界坐標系下坐標,如果i = 3是末端,那么第4列就是x、y了
因為:http://www.rzrgm.cn/pylblog/p/17962142
Pw = T03 P
P = [a3 , 0, 1],將P寫出一個平移矩陣,就是上面例子的 03T
所以:03T 陣的每個元素,都可以根據給定Φ,x,y得到具體值,然后再推算θ1,θ2,θ3
(這點尤其重要,必須知道03T 陣的每個元素的具體值)
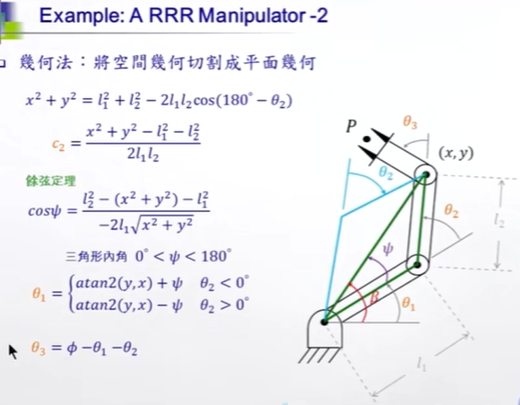


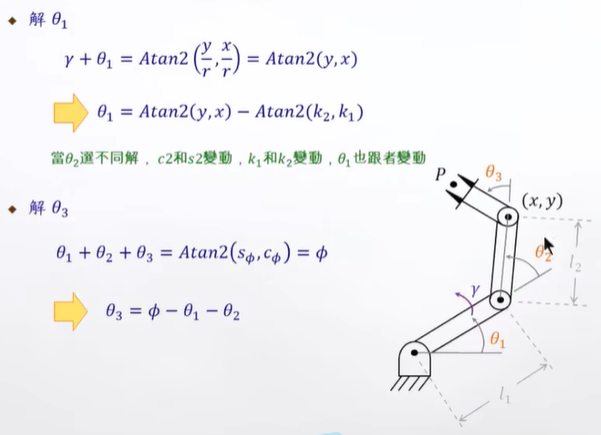
復雜的三角函數求解:


先知道"手腕"的位置,獲得θ1,θ2,θ3。
用Craig定義方式,得到通用的轉換陣
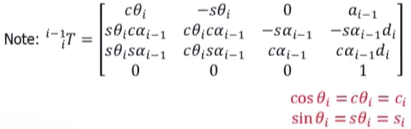
按照定義的步驟,一步步變過去,第四列就是變換后原點的坐標。


Pi = T ii-1* Pi-1, 當 Pi-1 = [ 0,0,0,1 ]T,即局部坐標系下的原點,那么T ii-1 的第四列,則為Pi
令:
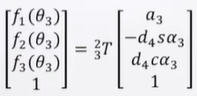
因為對于上面那個手臂:
沿X3方向看,Z3,Z4軸的夾角α3是已知,為90度;
沿X3方向看,Z3,Z4軸的距離a3是已知,就是臂長;
沿Z4方向看,X3,X4軸的距離d4是已知,應該為0;

因此:P4org,局部坐標,完全是已知的,往前推一步,得到:
P24org = T23P34org = [f1(θ3),f2(θ3),f3(θ3),1] T即:
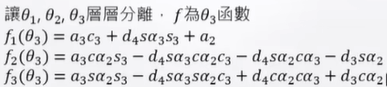
只有θ3是未知數。
再拆一次:
P14org = T12P24org = [g1(θ2,θ3) , g2(θ2,θ3) , g3(θ2,θ3) , 1] T即:

將 r = x2 + y2 + z2,消去θ1
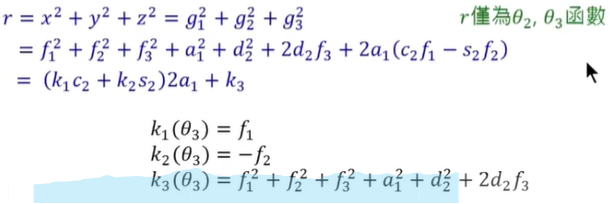

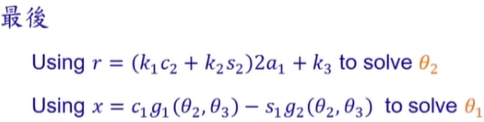
例子:
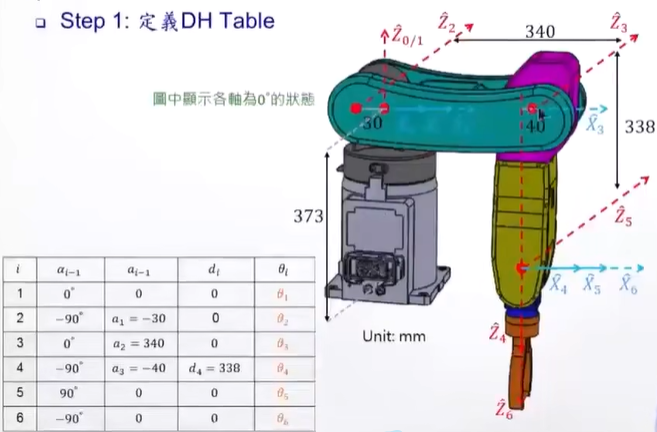

35°,是用視覺,或者其他設計系統,計算出來的,屬于已知的東西。
***θ1貌似可以直接定35
也就是,如果知道物體在桌子的哪個位置,那么至少可以定下DH表上,最前或者最后的一個角度,消掉1到2個未知數。
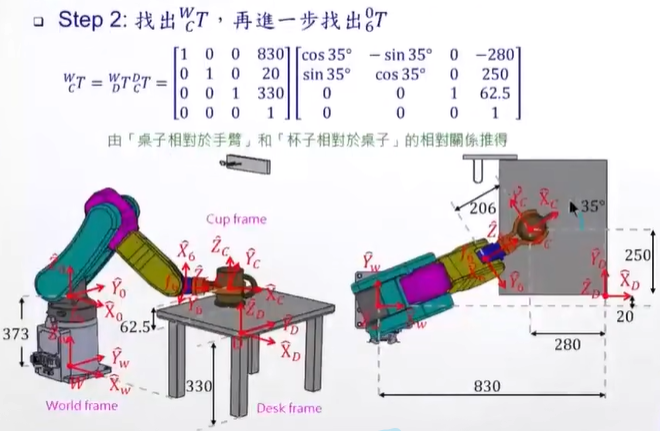
第一步:找到Twc,就是世界系 - 物體中心系之間的轉換。

第二步:找到Tw0 、T6c , 求出T06
Tw0 就是基座高度相關
T6c 就是物體中心到第6關節的轉換
都是屬于已知的,根據尺寸可以算出。
而T06 的第四列,就是6系原點,相對于0系系的坐標:P06org
由于4系、6系的原點是同一個,因此P06org = P04org
第三步:計算θ1、θ2、θ3
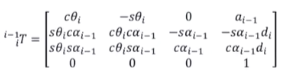
(注意到,第四列是和θ無關的)

得到:
代入第四列,直接得到P34org


第四步: θ1、θ2、θ3 , 得到R03,然后根據 R06 已知,得到R36




 浙公網安備 33010602011771號
浙公網安備 33010602011771號