運(yùn)動(dòng)控制理論(2)——實(shí)踐例子
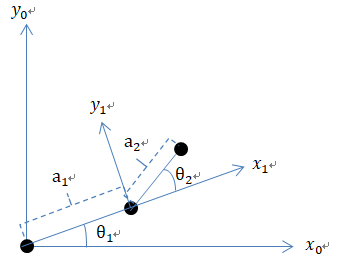
目的:要知道末端點(diǎn)的位置。
直觀的向量法
最直接的辦法,以向量相加的形式求。
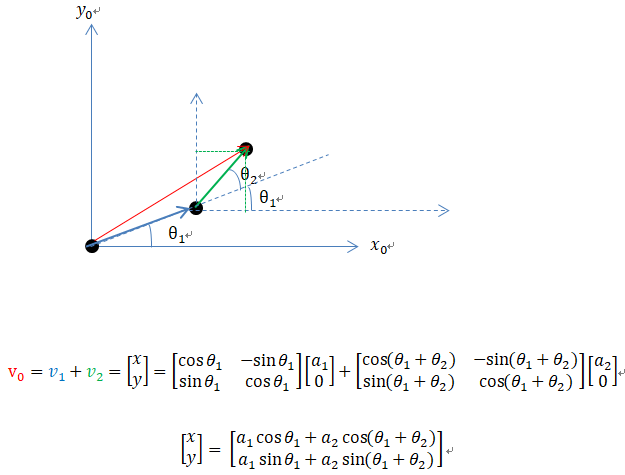
*3個(gè)向量都是參考0系構(gòu)建。
坐標(biāo)轉(zhuǎn)換法
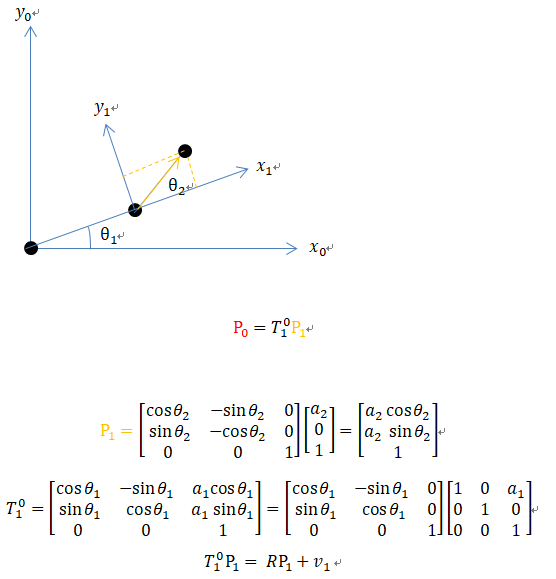
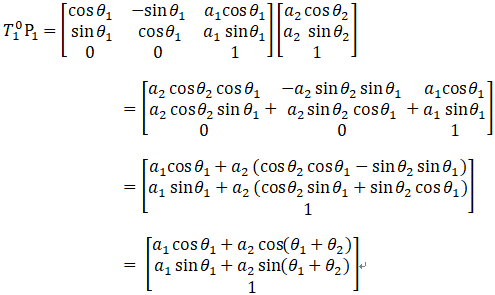
p1 是以1系下的局部坐標(biāo)。
R是旋轉(zhuǎn)矩陣,各列是以0系為參考的正交基。
v1是平移向量,也是以0系為參考的。
合并起來變成了T。
T = R3*3t3*3 ,將旋轉(zhuǎn)和平移分開兩個(gè)矩陣,從左往右看,就像旋轉(zhuǎn)了,然后沿旋轉(zhuǎn)后的X軸平移a1,到達(dá)了第二個(gè)關(guān)節(jié)一樣
多軸的例子
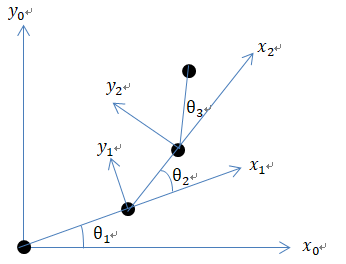
直觀的向量法求解
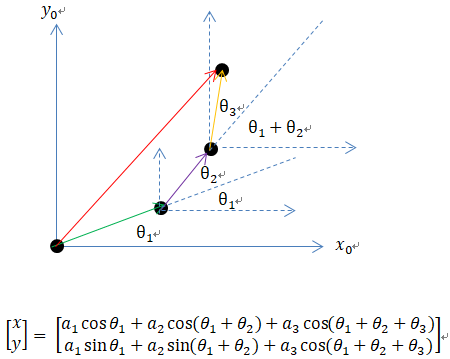
使用坐標(biāo)轉(zhuǎn)換的方式:
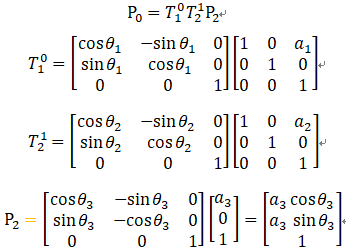

兩者結(jié)果相同!
結(jié)論:
1. 以旋轉(zhuǎn)、平移拆分,更容易寫出不出錯(cuò)的T
2. 從左往右像,好像 : 旋轉(zhuǎn)——沿旋轉(zhuǎn)后的軸移動(dòng)到下一個(gè)節(jié)點(diǎn)——旋轉(zhuǎn)——沿旋轉(zhuǎn)后的軸移動(dòng)到下一個(gè)節(jié)點(diǎn), 最后再乘以局部坐標(biāo)。
P0 = R01 *T1* R12 * T2...Rn-1n * TnPn

如果是不是最末端,Tx3[L3,0,0] 就是一個(gè)3*3陣,第3列就是末端的坐標(biāo)。
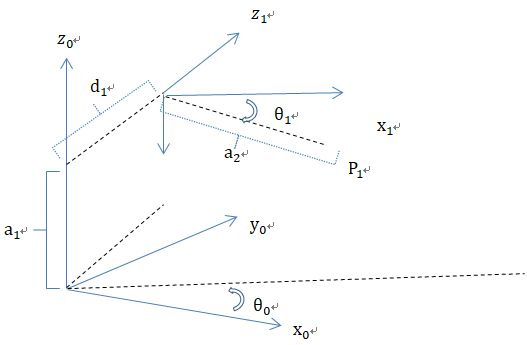
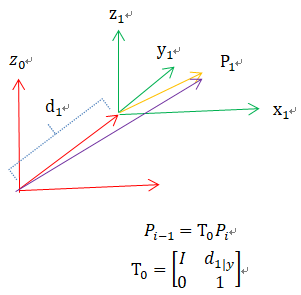
將每一步拆分,看成是后面局部坐標(biāo),轉(zhuǎn)換為前面整體坐標(biāo)

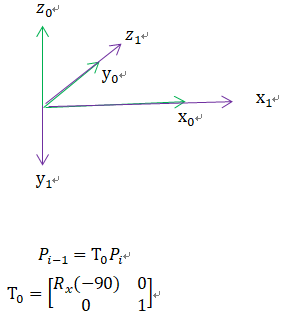

![]()
posted on 2024-01-13 11:29 耀禮士多德 閱讀(56) 評(píng)論(0) 收藏 舉報(bào)


 浙公網(wǎng)安備 33010602011771號(hào)
浙公網(wǎng)安備 33010602011771號(hào)