動態(tài)規(guī)劃題單2

二

第一個題單編輯到后面實在是太卡了，就新開了一個，以后應該也會 $30$ 題為一個題單。

31.CF1580D Subsequence

不會笛卡爾樹，但是看到題解區(qū)的妙妙解法......

題目的式子非常大便，我們考慮把它翻譯成人話:
一個子序列的價值為: $sum*m - 每兩個數(shù)及他們之間的所有數(shù)的\min$。

設 $f[l][r][k]$ 表示在 $[l,r]$ 中選出 $k$ 個數(shù)的最大代價(為了方便我們前面那一項不 $\times k$,而是還是$\times m$)。
假設 $[l,r]$ 的最小值位置是 $pos$,如果最后選出的數(shù)不跨越 $pos$,可以遞歸分治。
現(xiàn)在考慮跨越 $pos$ 的情況,我們有兩個轉移:

$f[l][pos-1][i]+f[pos+1][r][j] - 2 \times i \times j \times a[pos] \to f[l][r][i+j]$
$f[l][pos-1][i]+f[pos+1][r][j] + m\times a[pos] - [2\times (i+1) \times (j+1)-1] \times a[pos] \to f[l][r][i+j+1]$

我們來解釋一下:

不選擇 $a[pos]$,那么左端點在 $a[pos]$ 左邊，右端點在 $a[pos]$ 右邊的貢獻就是 $-2\times i\times j\times a[pos]$ ($\times 2$是因為每一對會貢獻兩次，因為題目中的 $j$ 是從 $1$ 開始，而不是 $i$)
選擇 $a[pos]$,那么左端點 $pos$ 或在 $a[pos]$ 左邊，右端點 $=pos$ 或在 $a[pos]$ 右邊的貢獻是 $-[2\times (i+1)\times (j+1)-1]\times a[pos]$ ，$-1$ 是因為當計算題目中的 $f$ 時左右端點都在 $pos$ 時只能貢獻一次

遞歸分治求解,時間復雜度可以近似認為是:
$T(n)=2 \times T(\frac{n}{2})+O(n^2)$
根據(jù)主定理他等于 $O(n^2)$

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,m,a[N]; 
vector<int> work(int l,int r){
	vector<int> f(r-l+2,LLONG_MIN);
	f[0]=0;
	if(l>r) return f;
	int pos=l;
	for(int i=l+1;i<=r;i++) if(a[pos]>a[i]) pos=i;
	vector<int> fl=work(l,pos-1),fr=work(pos+1,r);
	for(int i=0;i<fl.size();i++){
		for(int j=0;j<fr.size();j++){
			f[i+j]=max(f[i+j],fl[i]+fr[j]-2*i*j*a[pos]);
			f[i+j+1]=max(f[i+j+1],fl[i]+fr[j]+m*a[pos]-(2*(i+1)*(j+1)-1)*a[pos]);
		}
	} 
	return f;
}
signed main(){
	n=read(),m=read();
	for(int i=1;i<=n;i++) a[i]=read();
	printf("%lld\n",work(1,n)[m]);
	return 0;
}

32.P1220 關路燈

P1220 關路燈

經(jīng)典套路之——費用提前計算。

如果設 $f[l][r][0/1]$ 表示關掉區(qū)間 $[l,r]$ 內的路燈后,且最后停在 $l/r$,區(qū)間 $[l,r]$ 的路燈的最小花費。
不難想到是從 $f[l+1][r]$ 和 $f[l][r-1]$ 轉移過來。
但是轉移時我們無法知道從開始到現(xiàn)在經(jīng)過的時間，也就無法知道新加進來的路燈到底消耗了多少。

設 $f[l][r][0/1]$ 表示關掉區(qū)間 $[l,r]$ 內的路燈后,且最后停在 $l/r$,所有路燈的最小花費。
以從 $f[l+1][r][0]$ 轉移到 $f[l][r][0]$ 為例，在轉移時，我們不用再考慮在關 $[l+1,r]$ 內的路燈時的其他路燈的消耗。
只需要加上從 $l+1$ 走到 $l$ 這段時間里，$[1,l]$ 和 $[r+1,n]$ 路燈的功率消耗。
前綴和優(yōu)化一下即可，轉移顯然。

code

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,c,a[55],w[55],f[55][55][2];
int pre[55];
int calc(int l,int r){
	return pre[r]-pre[l-1];
}
signed main(){
	n=read(),c=read();
	for(int i=1;i<=n;i++){
		a[i]=read(),w[i]=read();
		pre[i]=pre[i-1]+w[i];
	}
	memset(f,0x3f,sizeof f);
	for(int len=1;len<=n;len++){
		for(int l=1;l+len-1<=n;l++){
			int r=l+len-1;
			if(c<l||c>r) continue;
			if(len==1) f[l][r][0]=f[l][r][1]=0;
			else{
				f[l][r][0]=min( f[l+1][r][0] + (a[l+1]-a[l])*(pre[n]-calc(l+1,r)) , f[l+1][r][1] + (a[r]-a[l])*(pre[n]-calc(l+1,r)) );
				f[l][r][1]=min( f[l][r-1][1] + (a[r]-a[r-1])*(pre[n]-calc(l,r-1)) , f[l][r-1][0] + (a[r]-a[l])*(pre[n]-calc(l,r-1)) );
			}
		}
	}
	printf("%d\n",min(f[1][n][0],f[1][n][1]));
	return 0;
}

33.搶鮮草

搶鮮草

和上題幾乎一模一樣。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=1e3+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,x,a[N];
int f[N][N][2];
/*
	考慮貢獻提前計算 
	f[l][r][0/1]: 表示kona采集完所有的 [l,r] 中的草，最后在 i/j 時，所有草的最小損失青草量
	(注意"所有") 
*/
signed main(){
	n=read(),x=read();
	for(int i=1;i<=n;i++) a[i]=read();
	sort(a+1,a+n+1);
	
	memset(f,0x3f,sizeof f); 
	for(int len=1;len<=n;len++){
		for(int l=1;l+len-1<=n;l++){
			int r=l+len-1;
			if(l==r){
				f[l][r][0]=f[l][r][1]=abs(a[l]-x)*n;	
			}
			else{
//				f[l][r][0]=min(f[l+1][r][0] + (a[l+1]-a[l]) * (n-(r-(l+1)+1)),f[l+1][r][1] + (a[r]-a[l]) * (n-(r-(l+1)+1)) );   //最原始的式子方便理解 
				f[l][r][0]=min(f[l+1][r][0] + (a[l+1]-a[l]) * (n-r+l),f[l+1][r][1] + (a[r]-a[l]) * (n-r+l));
				f[l][r][1]=min(f[l][r-1][1] + (a[r]-a[r-1]) * (n-r+l),f[l][r-1][0] + (a[r]-a[l]) * (n-r+l));
			}
		}
	}
	printf("%lld\n",min(f[1][n][0],f[1][n][1]));
	return 0;
}

34.P4161 [SCOI2009] 游戲

P4161 [SCOI2009] 游戲

如果把它根據(jù)對應關系連邊會得到若干環(huán)，假設第 $i$ 個環(huán)的環(huán)長為 $len[i]$。那么這個環(huán)里的數(shù)要恢復原樣就要 $len[i]$ 步。進一步的，容易得出整個序列要恢復原樣需要 $lcm(len[1],len[2],...)$。
問題轉化為:給你一個 $n$ , 構造若干個數(shù)，使得他們的和為 $n$, 求他們的 $lcm$ 的可能的情況數(shù)。

怎么構造出盡可能多的 $lcm$?
如果每一次這若干個數(shù)都互質，那他們的 $lcm = 他們的乘積$，從而每一次都不一樣。
具體的，我們只需要讓每個數(shù)都形如 $pi^{ki}$ ($pi$是質數(shù)，$ki$是非負整數(shù)) ，那根據(jù)算數(shù)基本定理，只要方案不同，他們的乘積($lcm$)就不同。

小小的證明：如果有一個構造方案，里面的數(shù)不互質，我們完全可以把它們轉換成形如上述的數(shù)列(每個質因子只保留對應的一個數(shù)),并且 $lcm$ 不變，而且他們的總和會變小，我們只需要再往里面塞 $1$ ,就可以了。
即任意一個情況都可以轉化成上述構造方法。

設 $f[i][j]$ 表示用前 $i$ 個質數(shù)，湊出和為 $j$ 的方案數(shù),$f[i][j]=f[i-1][j-(prime_i)^k]$，因為可以往里面塞好多個 $1$ ，所以我們欽定 $k>0$；因為 $i$ 可以不選，所以 $f[i][j]+=f[i-1][j]$。
初始化 $f[0][0]=1$。
最后的答案是 $\sum_{j=0}^{n} f[max_i][j]$ ($max_i$ 是最大的不超過 $n$ 的質數(shù)) 。

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e3+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n;
bool stater[N];
int cnt,pri[N];
void Eular(int n){
	stater[1]=1;
	for(int i=2;i<=n;i++){
		if(!stater[i]) pri[++cnt]=i;
		for(int j=1;j<=cnt&&i*pri[j]<=n;j++){
			stater[i*pri[j]]=true;
			if(i%pri[j]==0) break;
		}
	}
}
int f[N][N];
signed main(){
	n=read();
	Eular(n); 
	
	f[0][0]=1;
	for(int i=1;i<=cnt;i++){
		for(int j=0;j<=n;j++){
			f[i][j]=f[i-1][j];
			for(int k=pri[i];k<=j;k*=pri[i]) f[i][j]+=f[i-1][j-k];
		}
	}
	int ans=0;
	for(int j=0;j<=n;j++) ans+=f[cnt][j];
	printf("%lld\n",ans);
	return 0;
}

35.P6280 [USACO20OPEN] Exercise G

P6280 [USACO20OPEN] Exercise G

這題和上一題基本上是一樣的。

一樣的圖論連邊得出每個排列需要的步數(shù)為$lcm(len[i])$。
一樣的分析過程:我們只需要讓每個數(shù)都形如 $pi^{ki}$ ($pi$是質數(shù)，$ki$是非負整數(shù))。
基本一樣的DP狀態(tài)：
$f[i][j]$ 表示用前 $i$ 個質數(shù)，湊出和為 $j$ 的所有 $lcm$ 的和。
基本一樣的轉移:$f[i][j]=f[i-1][j-(prime_i)^k]*(prime_i)^k$ (因為互素，所以直接乘以 $i^k$ 就是新的 $lcm$)。
唯一不一樣的:$N=1e4$,所以滾動數(shù)組。

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e4+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,mod;
bool stater[N];
int cnt,pri[N];
void Eular(int n){
	stater[1]=1;
	for(int i=2;i<=n;i++){
		if(!stater[i]) pri[++cnt]=i;
		for(int j=1;j<=cnt&&i*pri[j]<=n;j++){
			stater[i*pri[j]]=true;
			if(i%pri[j]==0) break;
		}
	}
}
int f[N];
signed main(){
	n=read(),mod=read();
	Eular(n); 
	
	f[0]=1;
	for(int i=1;i<=cnt;i++){
		for(int j=n;j>=0;j--){
			for(int k=pri[i];k<=j;k*=pri[i]) (f[j]+=f[j-k]*k%mod)%=mod;
		}
	}
	int ans=0;
	for(int j=0;j<=n;j++) (ans+=f[j])%=mod;
	printf("%lld\n",ans);
	return 0;
}

36.P6570 [NOI Online #3 提高組] 優(yōu)秀子序列

一個數(shù)的二進制表示可以看成是一個集合。
設 $dp[i]$ 表示選出若干個互不相交的集合使他們的并為 $i$ 的方案數(shù),則答案是 $\sum dp[i] \times \phi(i+1)$。因為互不相交，所以他們的和也就等于他們的并等于 $i$。

我們先認為原序列沒有 $0$。
$dp[i]=∑dp[i \oplus j]*cnt[j]$ ($j$ 是 $i$ 的子集，$cnt[j]$ 表示原序列 $j$ 出現(xiàn)的次數(shù))。為了避免重復計算，當 $j < i \oplus j$ (補集) 時就退出。

對于有 $0$ 的情況，我們往里面可以塞任意多個 $0$ , 所以最后 $dp[i]=dp[i] \times 2^{cnt[0]}$。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int M=1e6+5,N=(1<<18)+5,mod=1e9+7;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,a[M];
int pri[N],tot;
bool stater[N];
int mn[N],mx[N],k[N],phi[N];
/*
	mn[i]:i的最小質因子
	mx[i]:i中所含 mn[i] 的最大冪
	k[i]:i中所含 mn[i] 的個數(shù)，mx[i]=mn[i]^k[i] 
	phi[i]:i的歐拉函數(shù) 
*/
void Eular()
{
	stater[1]=1;
	phi[1]=1;
	for(int i=2;i<N;i++)
	{
		if(!stater[i]) pri[++tot]=i,mn[i]=i,mx[i]=i,k[i]=1,phi[i]=i-1;
		for(int j=1;j<=tot&&i*pri[j]<N;j++)
		{
			int x=i*pri[j];
			stater[x]=true;
			mn[x]=pri[j];
			if(i%pri[j]==0)
			{
				mx[x]=mx[i]*pri[j];
				k[x]=k[i]+1;
				if(x!=mx[x]) phi[x]=phi[x/mx[x]]*phi[mx[x]];
				else phi[x]=x/mn[x] * (mn[x]-1);    
				/*
					phi(p^k) = p^k - p^(k-1)
							 = p^(k-1) * (p-1)
				*/
				break;
			}
			else
			{
				mx[x]=pri[j];
				k[x]=1;
				phi[x]=phi[i]*phi[pri[j]];
			}
		}
	}
}
int quick_power(int a,int b){
	int ans=1;
	while(b){
		if(b&1) (ans*=a)%=mod;
		(a*=a)%=mod,b>>=1;
	}
	return ans;
}
int Max(int m,int x){
	for(int i=x;i;i-=(i&-i)){
		m=max(m,(int)log2(i&-i));
	}
	return m;
}
int cnt[M],f[M];
signed main(){
	Eular();
	n=read();
	int m=0;
	for(int i=1;i<=n;i++) a[i]=read(),m=Max(m,a[i]),cnt[a[i]]++;
	m++;
	
	f[0]=1;
	for(int i=1;i<(1<<m);i++){
		for(int s=i;s>=(i^s);s=(s-1)&i){
			(f[i]+=f[i^s]*cnt[s]%mod)%=mod;
		}
	} 
	
	int ans=0;
	for(int i=0;i<(1<<m);i++) (f[i]*=quick_power(2,cnt[0]))%=mod;
	for(int i=0;i<(1<<m);i++) (ans+=f[i]*phi[i+1]%mod)%=mod;
	printf("%lld\n",ans);
	return 0;
}

37.CF1280D Miss Punyverse

CF1280D Miss Punyverse

考慮樹形DP。
把每個點的點權 $a[i]$ 設為 $w[i]-b[i]$，
這樣只要看 $a$ 之和是否 $>0$。

$f[u][i]$ 表示 $u$ 這棵子樹，分成 $i$ 個連通塊,不算包含 $u$ 的那一塊，最大的 $>0$ 的連通塊數(shù),這樣不是很轉移的動，因為在合并時我們需要知道包含 $u$ 的那一塊的權值之和。
考慮貪心，我們會發(fā)現(xiàn)有兩種比較理想的情況:

不算包含 $u$ 的那一塊，其余塊中滿足條件的塊記為 $cnt$,$cnt$ 盡可能大。
包含 $u$ 的那一塊，目前的權值記為 $val$,$val$ 盡可能大。

事實上，肯定是按照第一種情況貪心更優(yōu)，因為第二種情況里，$u$ 的那一塊權值再大也不過帶來 $1$ 的貢獻，無法彌補第一種情況帶來的貢獻差。

用pair來存儲兩種情況，$f[u][i].fi=cnt, f[u][i].se=val$。
我們只需要首先讓 $cnt$ 盡可能大，其次才是讓 $val$ 盡可能大。
邊界顯然是 $f[u][1]={0,a[u]}$。
每次新加入一個子節(jié)點 $v$, 我們有轉移:

包含 v 的那一塊單獨成一個連通塊: $f[u][i+j].fi=f[v][j].fi+f[u][i].fi+(f[v][j].se > 0)，f[u][i+j].se=f[u][i].se$。
轉移時要優(yōu)先按照第一維取max(pair自己內部就是這樣取max的，不用特殊處理) 。
包含 $v$ 的那一塊合進包含 $u$ 的那一塊: $f[u][i+j-1].fi=f[v][j].fi + f[u][i].fi ，f[u][i+j-1].se=f[v][j].se + f[u][i].se$。

為了防止轉移時用的 f 數(shù)組被更新過了，可以開一個輔助數(shù)組暫存,也可以倒序枚舉。

這個問題其實就是樹形背包，但是由于這是動態(tài)規(guī)劃題單系列第一道樹形背包題，所以簡要講一下:
對于一個狀態(tài) $f[u][i]$ 相當于有一個容積為 $i$ 的背包，每一個子節(jié)點 $v$ 對應著一組物品，第 $j$ 個物品大小為 $j$,價值為 $f[v][j]$,每組物品只能選一個(因為只能選一個轉移)，使得在不超過背包總體積的情況下(當然這道題因為轉移有點特殊其實不一定背包體積是 $i$)，價值的和(這道題里不是簡單相加)最大，即分組背包問題。
對于復雜度的分析雖然看起來有點像是 $O(n^3)$,
但注意到一次轉移我們其實可以認為是枚舉了任意兩個子樹的大小，也可以認為是分別枚舉了兩棵子樹內的點，一個點對最多只會在 $lca$ 處產(chǎn)生一個復雜度的貢獻，一共有 $n^2$ 個點對，所以復雜度為 $O(n^2)$。

code

#include<bits/stdc++.h>
typedef long long ll; 
#define PII pair<int,ll>
#define fi first
#define se second 
using namespace std;
const int N=3e3+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int T;
int n,m;
ll a[N];
int tot,head[N],to[N<<1],Next[N<<1];
void add(int u,int v){
	to[++tot]=v,Next[tot]=head[u],head[u]=tot;
} 
int Size[N];
PII f[N][N],tmp[N];
void dfs(int u,int fa){
	Size[u]=1;
	for(int i=0;i<=n;i++) f[u][i]={INT_MIN,INT_MIN};
	f[u][1]={0,a[u]};
	for(int i=head[u];i;i=Next[i]){
		int v=to[i];
		if(v==fa) continue;
		dfs(v,u);
		for(int j=1;j<=Size[u]+Size[v];j++) tmp[j]={INT_MIN,INT_MIN};
		for(int j=1;j<=min(m,Size[u]);j++){    //不要用填表法，會 TLE 
			for(int k=1;k<=min(m,Size[v]);k++){
				tmp[j+k]=max(tmp[j+k],{f[v][k].fi+f[u][j].fi+(f[v][k].se>0),f[u][j].se});
				tmp[j+k-1]=max(tmp[j+k-1],{f[v][k].fi+f[u][j].fi,f[v][k].se+f[u][j].se});
			}
		}
		for(int j=1;j<=Size[u]+Size[v];j++) f[u][j]=tmp[j];
		Size[u]+=Size[v];
	}
//	cout<<u<<':'<<'\n';
//	for(int i=1;i<=Size[u];i++){
//		cout<<i<<':'<<f[u][i].fi<<','<<f[u][i].se<<'\n';
//	}
}
void Init(){
	tot=0;;
	for(int i=1;i<=n;i++) head[i]=0,a[i]=0;
}
signed main(){
	T=read();
	while(T--){
		n=read(),m=read();
		Init();
		for(int i=1;i<=n;i++){
			ll b=read();
			a[i]-=b;
		}
		for(int i=1;i<=n;i++){
			ll w=read();
			a[i]+=w;
		}
		for(int i=1;i<n;i++){
			int u=read(),v=read();
			add(u,v),add(v,u);
		}
		dfs(1,0);
		printf("%d\n",f[1][m].fi+(f[1][m].se>0));
	}
	return 0;
}

38.CF1500D Tiles for Bathroom

CF1500D Tiles for Bathroom

注意到答案是單調的，一個大正方形里的小正方形都滿足
為了避免重復，我們對每個右下角統(tǒng)計答案。

考慮計算出 $f[i][j]$ 表示以 $(i,j)$ 為右下角，最大的合法正方形。

考慮從 $f[i-1][j-1]$ 的繼承過來，同時會新增第 $i$ 行和第 $j$ 列的貢獻。

因為 $q$ 很小，我們完全可以記錄對應的合法正方行里，每個顏色出現(xiàn)的最遠的位置(這個距離定義為切比雪夫距離，即 $\max(xi-xj,yi-yj)$ )。
所以為了方便更新，我們維護三個隊列:

$left[i][j]$: $(i,j)$左邊前 $q+1$ 個顏色的位置(同一種顏色取切比雪夫距離最小的,下同)
$up[i][j]$: $(i,j)$上邊前 $q+1$ 個顏色的位置
$lu[i][j]$: $(i,j)$左上方(即$1 \le x \le i,1 \le y \le j$)所有的元素中，前 $q+1$ 個顏色的位置。

$left$ 和 $up$ 的更新很容易，只需要加進來 $(i,j)$ 即可。
看一下 $lu[i][j]$：只需要從 $left[i][j-1]$,$up[i-1][j]$,$lu[i-1][j-1]$,$(i,j)$ 中不斷取最小的即可，
維護時要滿足三個隊列內的元素與 $(i,j)$ 的切比雪夫距離始終單調遞增。

計算 $f[i][j]$ 時，如果 $lu[i][j]$ 的個數(shù)不超過 $q$,那就是 $f[i][j]=min(i,j)$。
否則 $f[i][j]$ 為 $lu[i][j]$ 的第 $q+1$ 個顏色與 $(i,j)$ 的切比雪夫距離 $-1$。
時間復雜度:$O(n^2 \times q)$。

注意到這題卡空間，所以存位置的時候不要用 $pair$ , 把它變成一個數(shù)。
代碼有點丑。

code

#include<bits/stdc++.h>
#define PII pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=1505;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,q,a[N][N];
int ans[N]; 
int PairToNum(PII u){   //把坐標 (x,y) 變成數(shù)字 
	return (u.fi-1)*n+(u.se-1); 
}
PII NumToPair(int pos){ //把數(shù)字 變成 坐標
	return {pos/n+1,pos%n+1};
}
struct Queue{
	int q[12]; 
	int head=0,tail=-1;
	bool empty(){return tail<head;}
	void push(PII x){
		q[++tail]=PairToNum(x);
	}
	void pop(){
		++head;
	}
	void pop_back(){
		--tail;
	}
	PII front(){
		if(empty()) return {0,0}; 
		return NumToPair(q[head]);
	}
	int size(){return tail-head+1;};
}L[N][N],U[N][N],LU[N][N];
int calc(PII u,PII v){   //計算切比雪夫距離(真正的是不用+1的，這里要計算正方形邊長所以加一))
	return max(abs(u.fi-v.fi),abs(u.se-v.se))+1;
}

bool flag[N*N];
signed main(){
	n=read(),q=read();
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			a[i][j]=read();
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			L[i][j].push({i,j});
			for(int k=L[i][j-1].head;k<=L[i][j-1].tail;k++){
				PII u=NumToPair(L[i][j-1].q[k]);
				if(a[u.fi][u.se]==a[i][j]) continue;;
				L[i][j].push(u);
			}
			if(L[i][j].size()>q+1) L[i][j].pop_back();
			
			U[i][j].push({i,j});
			for(int k=U[i-1][j].head;k<=U[i-1][j].tail;k++){
				PII u=NumToPair(U[i-1][j].q[k]);
				if(a[u.fi][u.se]==a[i][j]) continue;;
				U[i][j].push(u);
			}
			if(U[i][j].size()>q+1) U[i][j].pop_back();
			
			LU[i][j].push({i,j});
			flag[a[i][j]]=true;   //記錄這種顏色是否出現(xiàn)過 
			int t1=L[i][j-1].head,t2=U[i-1][j].head,t3=LU[i-1][j-1].head;
			while(LU[i][j].size()<=q && (!L[i][j-1].empty() || !U[i-1][j].empty() || !LU[i-1][j-1].empty())){
				PII u=L[i][j-1].front(),v=U[i-1][j].front(),w=LU[i-1][j-1].front();
				 
				int d1=calc(u,{i,j}),d2=calc(v,{i,j}),d3=calc(w,{i,j}),mind=min({d1,d2,d3});   //取最小的那一個 
				if(mind==d1 && !L[i][j-1].empty()){
					L[i][j-1].pop();
					if(flag[ a[u.fi][u.se] ]) continue;  //出現(xiàn)過就忽略了 
					LU[i][j].push(u);
					flag[ a[u.fi][u.se] ]=true;	
				} 
				else if(mind==d2 && !U[i-1][j].empty()){
					U[i-1][j].pop();
					if(flag[ a[v.fi][v.se] ]) continue;
					LU[i][j].push(v);
					flag[ a[v.fi][v.se] ]=true;
				} 
				else{
					LU[i-1][j-1].pop();
					if(flag[ a[w.fi][w.se] ])continue;
					LU[i][j].push(w);
					flag[ a[w.fi][w.se] ]=true;
				}
			}
			L[i][j-1].head=t1,U[i-1][j].head=t2,LU[i-1][j-1].head=t3;
			for(int k=LU[i][j].head;k<=LU[i][j].tail;k++){
				PII u=NumToPair( LU[i][j].q[k] );
				flag[a[u.fi][u.se]]=false;
			} 
			
			int tmp=min(i,j);
			if(LU[i][j].size()==q+1) tmp=min(tmp,calc( NumToPair(LU[i][j].q[LU[i][j].tail]) , {i,j} )-1); 
			ans[tmp]++;
		} 
	}
	
	for(int i=n;i>=1;i--) ans[i]+=ans[i+1];
	for(int i=1;i<=n;i++) printf("%d\n",ans[i]);
	return 0;
}

39.CF1276D Tree Elimination

CF1276D Tree Elimination

神仙分類討論樹形DP題，按照連向父親的邊什么時候被刪的分類討論一下，因為 LaTex 打起來太煩了，所以具體看題解區(qū)的吧。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=2e5+5,mod=998244353;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n;
vector<int> G[N];  //vector存邊天然優(yōu)勢:編號大的在后面 
int f[N][4],pre[N],suf[N];
void dfs(int u,int fa){
	bool flag=false;  //編號是否比 (u,fa) 大 
	f[u][1]=f[u][3]=1;
	for(int v:G[u]){
		if(v==fa){
			flag=true;
			continue;
		} 
		dfs(v,u);
		(f[u][3]*=(f[v][0]+f[v][1])%mod)%=mod;
		if(!flag){
			(f[u][1]*=(f[v][0]+f[v][1])%mod)%=mod;  //此時 u 還在 
		}
		else{
			(f[u][1]*=(f[v][0]+f[v][2]+f[v][3])%mod)%=mod;   //此時 u 已經(jīng)沒了
		}
	}
	pre[0]=1;
	for(int i=1;i<=G[u].size();i++){
		int v=G[u][i-1];
		if(v==fa){
			pre[i]=pre[i-1];
			continue;
		}
		(pre[i]=pre[i-1]*(f[v][0]+f[v][1])%mod)%=mod;
	}
	suf[G[u].size()+1]=1;
	for(int i=G[u].size();i>=1;i--){
		int v=G[u][i-1];
		if(v==fa){
			suf[i]=suf[i+1];
			continue;
		}
		(suf[i]=suf[i+1]*(f[v][0]+f[v][2]+f[v][3])%mod)%=mod;
	}
	f[u][0]=f[u][2]=0;
	flag=false;
	for(int i=1;i<=G[u].size();i++){
		int v=G[u][i-1];
		if(v==fa){
			flag=true;
			continue;
		} 
		if(!flag){
			(f[u][0] += (f[v][2]+f[v][3])%mod * pre[i-1]%mod * suf[i+1]%mod)%=mod; 
		}
		else{
			(f[u][2] += (f[v][2]+f[v][3])%mod * pre[i-1]%mod * suf[i+1]%mod)%=mod;  
		}
	}
	
}
signed main(){
	n=read();
	for(int i=1;i<n;i++){
		int u=read(),v=read();
		G[u].push_back(v),G[v].push_back(u);
	}
	dfs(1,0);
	printf("%lld\n",(f[1][0]+f[1][2]+f[1][3])%mod);
	return 0;
}

40.P1081 [NOIP2012 提高組] 開車旅行

P1081 [NOIP2012 提高組] 開車旅行

經(jīng)典倍增優(yōu)化DP題。

預處理:
$a[i],b[i]$ 分別表示 $A/B$ 開車從 $i$ 開始，下一個到達的城市。
用 multiset 維護即可，不贅述
DP:

$f[i][j][k]$ 表示行駛 $2^i$ 天，從城市 $j$ 開始，$k$ 先開車會到的城市。
$sa[i][j][k]$ 表示行駛 $2^i$ 天，從城市 $j$ 開始，$k$ 先開車,小A開的距離。
$sb[i][j][k]$ 表示行駛 $2^i$ 天，從城市 $j$ 開始，$k$ 先開車,小B開的距離。
注意當 $i=0$ 時，$2^0=1$為奇數(shù)，轉移時要注意開車的人會變。其余就正常的轉移

calc函數(shù)：
$calc(s,x)$ 表示從 $s$ 開始，最多行駛 $x$,小A和小B分別會行駛的距離,倍增即可
回答詢問:
詢問一:只會問一次，暴力枚舉起點。
詢問二:直接輸出 $calc(si,xi)$。

code

#include<bits/stdc++.h>
#define PII pair<int,int>
#define fi first
#define se second
#define int long long 
using namespace std;
const int N=1e5+5,M=(1<<17)+5,inf=2e14;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,h[N];

int a[N],b[N];
multiset<PII> s;
multiset<PII>::iterator it1,it2; 
int dist(int x,int y){
	if(x==0||y==0) return inf;
	return abs(h[x]-h[y]);
}
int u;
bool cmp1(PII x,PII y){
	if(dist(x.se,u)==dist(y.se,u)) return x.fi<y.fi;
	return dist(x.se,u)<dist(y.se,u);
}
void Init(){
//	return;
	s.insert({inf,0}),s.insert({inf,0}),s.insert({-inf,0}),s.insert({-inf,0});
	//防止越界 
	for(int i=n;i>=1;i--){
		PII tmp[6];
		s.insert({h[i],i});
		it1=it2=s.find({h[i],i});
		--it1; tmp[1]=*it1;
		--it1; tmp[2]=*it1;
		++it2; tmp[3]=*it2;
		++it2; tmp[4]=*it2;
		u=i;
		sort(tmp+1,tmp+4+1,cmp1);
		a[i]=tmp[2].se,b[i]=tmp[1].se;
	}
}


int f[20][N][2],sa[20][N][2],sb[20][N][2];
void DP(){
	for(int i=1;i<=n;i++){
		f[0][i][0]=a[i],f[0][i][1]=b[i];
		sa[0][i][0]=dist(i,a[i]),sa[0][i][1]=0;
		sb[0][i][1]=dist(i,b[i]),sb[0][i][0]=0;
	}
	for(int i=1;i<=17;i++){
		for(int j=1;j<=n;j++){
			for(int k=0;k<=1;k++){
				if(i==1){
					f[i][j][k]=f[i-1][ f[i-1][j][k] ][1-k];
					sa[i][j][k]=sa[i-1][j][k] + sa[i-1][ f[i-1][j][k] ][1-k];
					sb[i][j][k]=sb[i-1][j][k] + sb[i-1][ f[i-1][j][k] ][1-k];
				}
				else{
					f[i][j][k]=f[i-1][ f[i-1][j][k] ][k];
					sa[i][j][k]=sa[i-1][j][k] + sa[i-1][ f[i-1][j][k] ][k];
					sb[i][j][k]=sb[i-1][j][k] + sb[i-1][ f[i-1][j][k] ][k];
				}
			}
		}
	}
}

PII calc(int s,int x){
	int suma=0,sumb=0,sum=0;
	for(int i=17;i>=0;i--){
		if(f[i][s][0]&&(sum+sa[i][s][0]+sb[i][s][0])<=x){
			suma+=sa[i][s][0],sumb+=sb[i][s][0],sum=suma+sumb;
			s=f[i][s][0];
		}
	}
	return {suma,sumb};
}

struct frac{
	int a,b,id;
};
bool cmp(frac x,frac y){
	if(x.b==y.b&&x.b==0) return h[x.id]>h[y.id];
	if(y.b==0) return true;
	if(x.b==0) return false;
	if(x.a*y.b==y.a*x.b) return h[x.id]>h[y.id];
	return x.a*y.b<y.a*x.b;
}
void solve1(){
	int x0=read();
	frac ming={1,0,0};
	for(int i=1;i<=n;i++){
		int s1=calc(i,x0).fi,s2=calc(i,x0).se;
		if(cmp({s1,s2,i},ming)) ming={s1,s2,i};
	}	
	printf("%lld\n",ming.id);
}

void solve2(){
	int T=read();
	while(T--){
		int s=read(),x=read();
		printf("%lld %lld\n",calc(s,x).fi,calc(s,x).se);
	}
}
signed main(){
	n=read();
	h[0]=-inf;
	for(int i=1;i<=n;i++) h[i]=read();
	Init();
	DP();
	solve1();
	solve2();
	return 0;
}

41.P9197 [JOI Open 2016] 摩天大樓 / Skyscraper

P9197 [JOI Open 2016] 摩天大樓

~~其實這個在動態(tài)規(guī)劃題單一應該就要寫了，但是太懶了，所以拖到現(xiàn)在。~~

套路和 [CEOI2016] kangaroo 有點類似(在第一個題單里)，所以建議先看那題。
那我們先列出狀態(tài): $f[i][j][k][0/1][0/1]$ 表示從大到小放到第 $i$ 個數(shù)，一共有 $j$ 個連續(xù)段，題目里的式子計算結果為 $k$,放/沒放第一個，放/沒放最后一個的方案數(shù)。
但這樣如果我們每一次新放進來一個數(shù)，只是計算他和他兩邊的數(shù)新增的貢獻，我們還需要記錄整個序列的哪些位置填了哪些數(shù)，才能轉移動 $k$,但這樣狀態(tài)就炸了。所以我們考慮轉換一下計算 $|f_1-f_2| + |f_2-f_3| +...+ |f_{N-1}-f_N|$ 的計算方法。

假如最后是這么個填數(shù)方案，橫坐標是下標，縱坐標是數(shù)值。

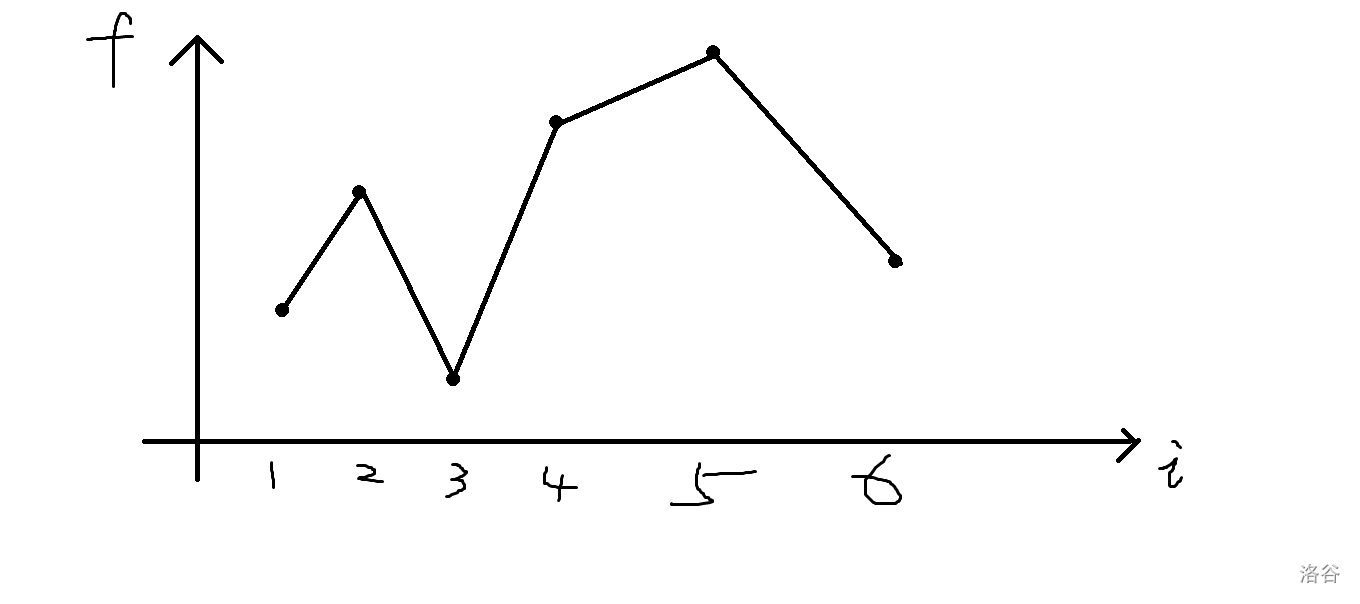
所以當我們從大到小填到第四個數(shù)的時候(即圖中的$f_6$),我們按照原始的方法其實只計算了圖中綠色的線段的值。

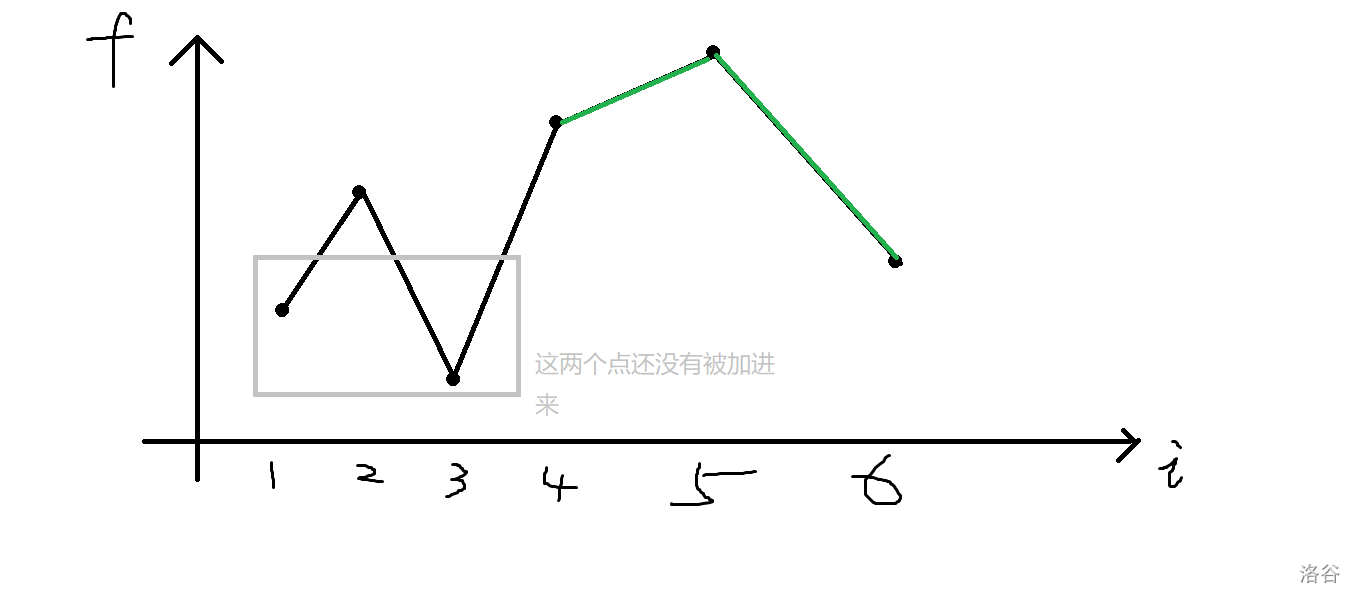
這就使得我們再加進第五個點的時候很不好計算多出來的答案，所以我們計算答案的方式變?yōu)?
當新放進來一個數(shù) $a_i$ 時，假設現(xiàn)在的段數(shù)是 $j$,那么把答案累加上 $(a_{i-1}-a_i) \times (2j)$,意思是每一段自動在兩側延伸 $(a_{i-1}-a_i)$,也可以看作是提前計算貢獻。

這樣當我們從大到小填到第四個數(shù)的時候,我們其實就計算了圖中藍色部分的線段了。

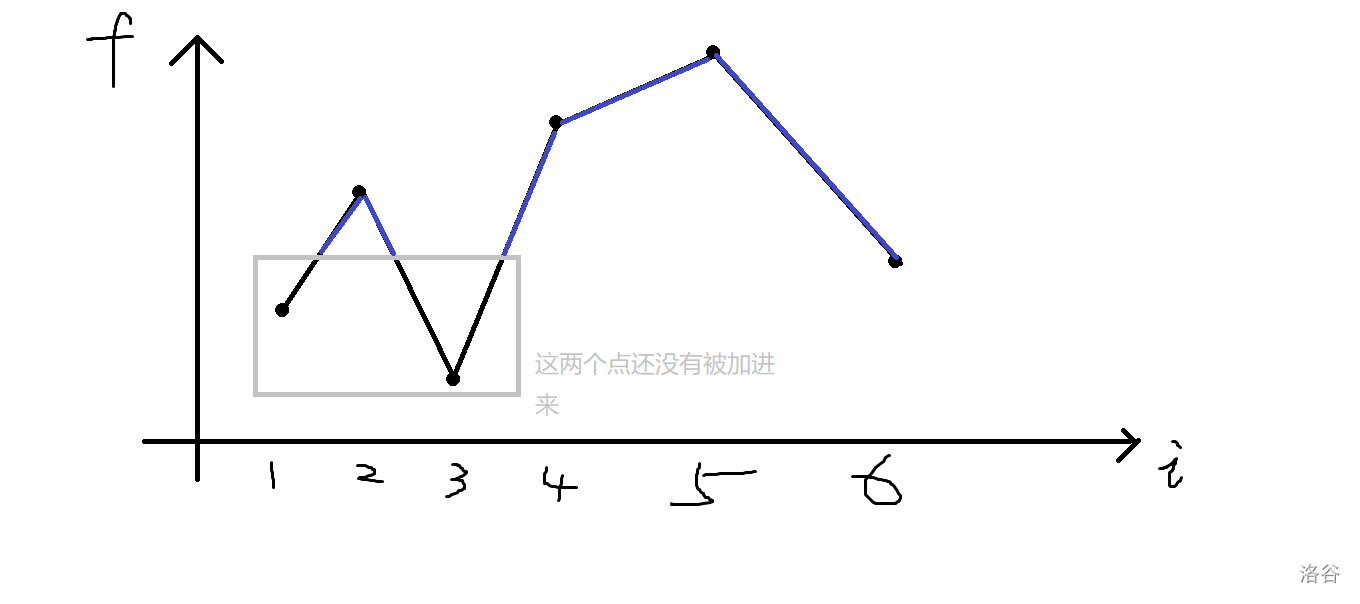
但這樣還是會有個小問題，就是在加第$5$個點時，按照上述算法，多出來的答案是圖中紅色加上黃色線段。
但其實黃色線段是沒有的。

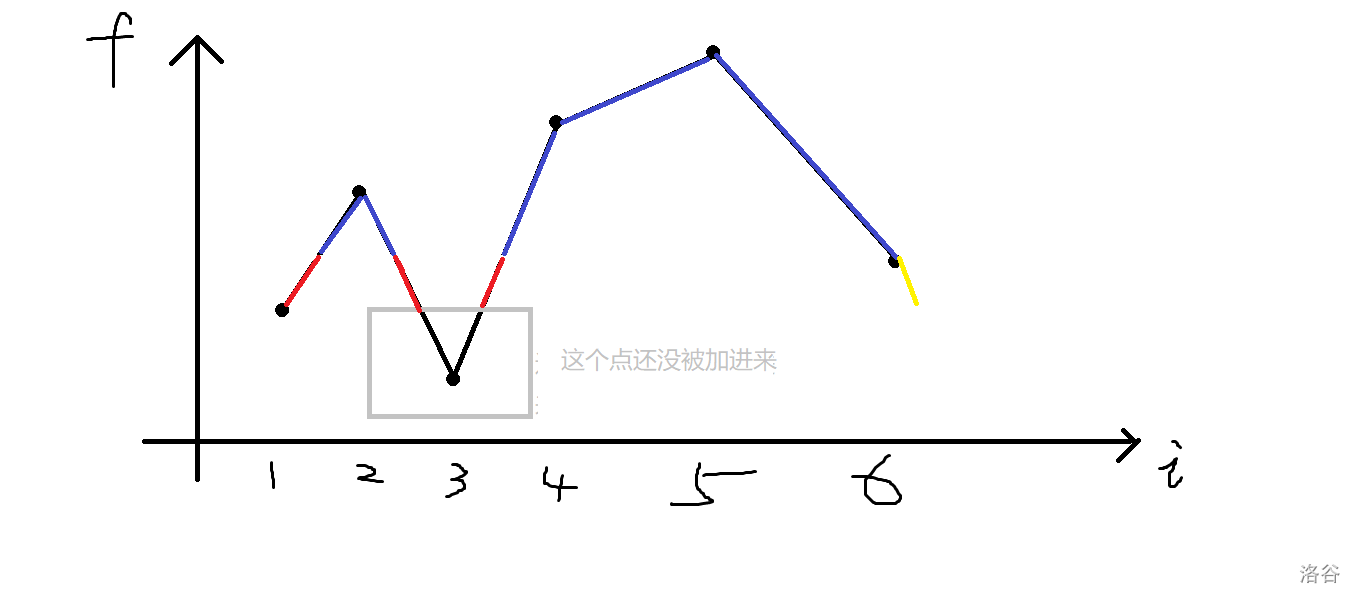
解決辦法也比較簡單，在開頭和結尾已經(jīng)放了的情況下轉移特判一下即可。

具體細節(jié)見代碼。

code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5,mod=1e9+7;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,L,a[105];
int f[105][105][1005][2][2];
/*
	f[i][j][k][0/1][0/1]表示從大到小放到第 i 個數(shù)，一共有j個連續(xù)段，題目里的式子計算結果為 k,放/沒放第一個，放/沒放最后一個 
*/
signed main(){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	n=read(),L=read();
	for(int i=1;i<=n;i++) a[i]=read();
	if(n==1){
		cout<<1<<'\n';
		return 0;   // 此時它又是開頭，又是結尾 
	}
	sort(a+1,a+n+1,greater<int>());
	
	f[0][0][0][0][0]=1; 
	for(int i=0;i<=n;i++){
		for(int j=0;j<=i;j++){
			for(int k=0;k<=L;k++){
				int sum;  //新增貢獻
				 
				//從f[i][j][k][0][0]轉移
				sum=k + 2 * j * (a[i] - a[i+1]);
				if(sum<=L&&sum>=0){
					//1.i+1放開頭
					( f[i + 1][j + 1][sum][1][0] += f[i][j][k][0][0] ) %= mod;   //自成一段 
					( f[i + 1][j][sum][1][0] += f[i][j][k][0][0] ) %= mod;     //粘在一段前面 
					//2.i+1放結尾
					( f[i + 1][j + 1][sum][0][1] += f[i][j][k][0][0] ) %= mod;   //自成一段 
					( f[i + 1][j][sum][0][1] += f[i][j][k][0][0] ) %= mod;     //粘在一段后面 
					//3.i+1放中間
		 			( f[i + 1][j + 1][sum][0][0] += (j + 1) * f[i][j][k][0][0] % mod ) %= mod; //自成一段 
					( f[i + 1][j][sum][0][0] += 2 * j * f[i][j][k][0][0] % mod ) %= mod;  //粘在一段前面/后面
					( f[i + 1][j - 1][sum][0][0] += (j - 1) * f[i][j][k][0][0] % mod) %= mod;  //把兩段粘在一起 
				}
				
				//從f[i][j][k][1][0]轉移 
				sum=k + (2 * j - 1) * (a[i] - a[i+1]);
				if(sum<=L&&sum>=0){
					//1.i+1放結尾
					( f[i + 1][j + 1][sum][1][1] += f[i][j][k][1][0] ) %= mod;   //自成一段 
					( f[i + 1][j][sum][1][1] += f[i][j][k][1][0] ) %= mod;     //粘在一段后面
					//2.i+1放中間,不能放開頭了 
		 			( f[i + 1][j + 1][sum][1][0] += j * f[i][j][k][1][0] % mod ) %= mod; //自成一段 
					( f[i + 1][j][sum][1][0] += (2 * j - 1) * f[i][j][k][1][0] % mod ) %= mod;  //粘在一段前面/后面
					( f[i + 1][j - 1][sum][1][0] += (j - 1) * f[i][j][k][1][0] % mod) %= mod;  //把兩段粘在一起
				}
				
				//從f[i][j][k][0][1]轉移
				sum=k + (2 * j - 1) * (a[i] - a[i+1]);
				if(sum<=L&&sum>=0){
					//1.i+1放開頭
					( f[i + 1][j + 1][sum][1][1] += f[i][j][k][0][1] ) %= mod;   //自成一段 
					( f[i + 1][j][sum][1][1] += f[i][j][k][0][1] ) %= mod;     //粘在一段前面 
					//2.i+1放中間,不能放結尾了 
		 			( f[i + 1][j + 1][sum][0][1] += j * f[i][j][k][0][1] % mod ) %= mod; //自成一段 
					( f[i + 1][j][sum][0][1] += (2 * j - 1) * f[i][j][k][0][1] % mod ) %= mod;  //粘在一段前面/后面
					( f[i + 1][j - 1][sum][0][1] += (j - 1) * f[i][j][k][0][1] % mod) %= mod;  //把兩段粘在一起	
				}
				
				//從f[i][j][k][1][1]轉移
				sum=k + (2 * j - 2) * (a[i] - a[i+1]);
				if(sum<=L&&sum>=0){
					//1.i+1放中間,不能放開頭和結尾了 
		 			( f[i + 1][j + 1][sum][1][1] += (j - 1) * f[i][j][k][1][1] % mod ) %= mod; //自成一段 
					( f[i + 1][j][sum][1][1] += (2 * j - 2) * f[i][j][k][1][1] % mod ) %= mod;  //粘在一段前面/后面
					( f[i + 1][j - 1][sum][1][1] += (j - 1) * f[i][j][k][1][1] % mod) %= mod;  //把兩段粘在一起	
				}
			}
		}
	} 
	
	int ans=0;
	for(int i=0;i<=L;i++){
		(ans += f[n][1][i][1][1]) %= mod;
	}
	printf("%lld\n",ans);
	return 0;
}

42.Count The Repetitions*

Count The Repetitions*

$[S2，M]=[s2,n2*M]$。
找到最大的 $M$ 也就是找到最大的 $M'$ 使得 $[S2,M']$ 是 $[s1,n1]$ 的子序列。答案那就是 $\lfloor \frac {M'} {n2} \rfloor$ 。

無解的判定:如果 $s2$ 中的字符沒有全部在 $s1$ 中出現(xiàn)就無解。否則至多重復 $s1$ $len2$ 次就可以得到一個 $s2$ ($len2$ 是 $s2$ 的長度)。

預處理:$g[i]$ 表示從 $s1$ 的第 $i$ 位開始，至少接需要多少個字符才能湊出一個 $s2$，注意不是接多少個 $s1$,而是字符,$O(len^3)$ 暴力即可

設 $f[i][s]$ 表示從 $s1$ 的第 $s$ 個開始,湊出 $2^i$ 個 $s2$ 需要多少個字符,轉移顯然。

倍增優(yōu)化求答案的過程即可。

code


#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=1e5+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
char s1[105],s2[105];
int n1,n2,len1,len2;
int g[105],f[40][105];
bool stater;
void Init(){
	memset(g,0x3f,sizeof g);
	memset(f,0x3f,sizeof f);
	len1=strlen(s1),len2=strlen(s2);
	stater=true;
	string s;
	for(int i=1;i<=len2;i++) s=s+s1;
	for(int i=0;i<len1;i++){
		int k=0;
		for(int j=i,cnt=1;j<s.size();j++,cnt++){
			if(s[j]==s2[k]){
				k++;
				if(k==len2){
					g[i]=cnt;
					break;
				}
			}
		}
		if(g[i]>s.size()){
			stater=false;
			return;
		}
		else f[0][i]=g[i];
	}
	for(int t=1;t<=30;t++){
		for(int i=0;i<len1;i++){
			f[t][i]=f[t-1][i]+f[t-1][(i+f[t-1][i])%len1];
		}
	}
}
void work(){
	if(!stater){
		puts("0");
		return;
	}
	int maxn=len1*n1,sum=0,res=0,pos=0;
	for(int i=30;i>=0;i--){
		if(f[i][pos]+sum<=maxn){
			sum+=f[i][pos];
			pos=(pos+f[i][pos])%len1;
			res+=pow(2,i);
		}
	}
	printf("%lld\n",res/n2);
}
signed main(){
	 while(scanf("%s %lld\n%s %lld",s2,&n2,s1,&n1)==4){
		Init();
		work();
	}
	return 0;
}

43.CF1788E Sum Over Zero

CF1788E Sum Over Zero

$f[i]$:表示區(qū)間 $[1,i]$ 上的最大值 (一定要選 $i$)。
$pre[i]$:表示 $max{f[0],f[2],...,f[i]}$。
$s[i]=a1+a2+...+ai$。

轉移:$f[i]=max_{0 \le j \le i-1,si-sj \ge 0}({i-j+pre[j]})$

$f[i]$ 轉移的優(yōu)化:在每個 $s[j]$ 上記錄最大的 $pre[j]-j$ , 轉移時在線段樹上查詢 $(-inf,si]$ 的最大值。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=2e5+5,MAXN=2e14;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,a[N];
int s[N],pre[N],f[N];
int dis[N],m;
int Dis(int x){
	return lower_bound(dis+1,dis+m+1,x)-dis; 
}
struct node{
	int l,r,maxn;
};
struct SegmentTree{
	node t[10000005];
	void pushup(int p){
		t[p].maxn=max(t[p<<1].maxn,t[p<<1|1].maxn);
	}
	void build(int p,int l,int r){
		t[p].l=l,t[p].r=r,t[p].maxn=LLONG_MIN;
		if(l==r) return;
		int mid=(l+r)>>1;
		build(p<<1,l,mid);
		build(p<<1|1,mid+1,r);
		pushup(p);
	}
	void change(int p,int x,int val){
		if(t[p].l==t[p].r){
			t[p].maxn=max(t[p].maxn,val);
			return;
		}
		int mid=(t[p].l+t[p].r)>>1;
		if(x<=mid){
			change(p<<1,x,val);
		}
		else{
			change(p<<1|1,x,val);
		}
		pushup(p);
	}
	int ask(int p,int l,int r){
		if(l<=t[p].l&&t[p].r<=r){
			return t[p].maxn;
		}	
		int mid=(t[p].l+t[p].r)>>1,res=LLONG_MIN;
		if(l<=mid) res=max(res,ask(p<<1,l,r));
		if(r>mid) res=max(res,ask(p<<1|1,l,r));
		return res;
	}
}Seg;
signed main(){
	int ming=0;
	n=read();
	dis[n+1]=0;
	for(int i=1;i<=n;i++) a[i]=read(),s[i]=s[i-1]+a[i],dis[i]=s[i],ming=min(ming,s[i]);
	sort(dis+1,dis+n+1+1);
	m=unique(dis+1,dis+n+1+1)-dis-1; 
	
	Seg.build(1,1,m);
	f[0]=0;
	pre[0]=0;
	Seg.change(1,Dis(s[0]),pre[0]);
	for(int i=1;i<=n;i++){
		f[i]=Seg.ask(1,Dis(ming),Dis(s[i]))+i;
		pre[i]=max(pre[i-1],f[i]);
		Seg.change(1,Dis(s[i]),pre[i]-i);
	}
	printf("%lld\n",pre[n]);
	return 0;
}

44.CF1799D2 Hot Start Up (hard version)

CF1799D2 Hot Start Up (hard version)

壓縮狀態(tài)優(yōu)化DP 。

$f[i][x][y]$ 表示處理完第 $i$ 個程序，目前第一個 CPU 里運行的程序種類是 $x$,第二個里運行的程序種類是 $y$。
因為 $x,y$ 中一定有一個是 $ai$,考慮把第一維去掉，那么有轉移(很明顯能用 $hot$ 就不用 $cold$):

$f[x][y]+cold[ai] \to f[ai][y]$
$f[x][y]+cold[ai] \to f[x][ai]$
$f[x][ai]+hot[ai] \to f[x][ai]$
$f[ai][x]+hot[ai] \to f[ai][x]$

直接跑是 $O(n\times k^2)$ 的

我們會發(fā)現(xiàn)每次轉移時，都只會轉移到 $f[ai][x]$ 或 $f[x][ai]$。同理在進行轉移的時候也只有 $f[a[i-1]][x]$ 和 $f[x][a[i-1]]$ 中會有值。只需要枚舉 $x$ ,進行轉移即可。

因為兩個 CPU 本質相同,所以 $f[x][y]$ 顯然等于$f[y][x]$，即轉移優(yōu)化成: (默認 $a[i-1] \ne a[i]$，如果相等直接全部加 $hot[ai]$ 即可)

$f[a[i-1]][x]+cold[ai] \to f[a[i-1]][ai]$ (此時如果 $x=ai$ 的話，肯定不如第3條優(yōu))
$f[a[i-1]][x]+cold[ai] \to f[ai][x]$
$f[a[i-1]][ai]+hot[ai] \to f[a[i-1]][ai]$

可以通過簡單版。

還是因為 $f[x][y]=f[y][x]$,所以轉移到 $f[ai][x]$ 和轉移到 $f[x][ai]$ 是一樣的，所以我們考慮進一步壓縮狀態(tài)用 $f[x]$ 代替 $f[ai][x]$，那么上面那三個轉移式子就優(yōu)化成:

如果 $a[i-1] \ne ai$

$f[x]+cold[ai] \to f[a[i-1]]$
$f[x]+cold[ai] \to f[x]$
$f[ai]+hot[ai] \to f[a[i-1]]$

分別進行優(yōu)化:

轉移到的目標是定的，直接維護全局最小值進行轉移即可。
相當于每個點都加一個 $cold[ai]$,我們用 $add$ 記錄一下全局累加標記即可。
下標都給定了，直接轉移。

如果 $a[i-1]=ai$,直接 $add+=hot[ai]$。

幾個注意:

如果進行了轉移1或3，那此時是不用加上轉移2的 $cold[ai]$ 的，要先減掉 $cold[ai]$。
維護新的全局最小值時全部重新跑一遍肯定不太對，我們會發(fā)現(xiàn)這三個轉移中只有轉移二會轉移到 $f[x]$,但是 $f[x]+cold[ai]$ 不僅會轉移給 $f[x]$,也會轉移給 $f[a[i-1]]$,而 $f[a[i-1]]$ 還可以通過 $f[ai]+hot[ai]$ 轉移,所以 $f[a[i-1]]$ 一定是全局最小值，只要用它更新即可。
3.一開始 $f[0]=0$, 其余全是 $inf$。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=3e5+5,inf=3e14+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int T;
int n,k,a[N],cold[N],hot[N],f[N];
void work(){
	n=read(),k=read();
	for(int i=1;i<=n;i++) a[i]=read();
	for(int i=1;i<=k;i++) cold[i]=read(),f[i]=inf;
	for(int i=1;i<=k;i++) hot[i]=read();
	f[0]=0;
	int add=0,ming=0;
	for(int i=1;i<=n;i++){
		if(a[i]!=a[i-1]){
			add+=cold[a[i]];
			f[a[i-1]]=min({f[a[i-1]] , ming+cold[a[i]]-cold[a[i]] , f[a[i]]+hot[a[i]]-cold[a[i]]});
			ming=f[a[i-1]];
		}
		else add+=hot[a[i]];
	}
	printf("%lld\n",ming+add);
}
signed main(){
	T=read();
	while(T--) work();
	return 0;
}

45.CF1304F2 Animal Observation (hard version)

CF1304F2 Animal Observation (hard version)

題意簡化:給定一個 $n\times m$ 的矩形，每一行選擇一個點，并以這個點為左上角框出一個 $2\times k$ 的小矩形,求所有小矩形的并所覆蓋的數(shù)字之和的最大值。

設 $m'=m-k+1$,顯然每個點的縱坐標不會超過 $m'$。

設 $f[i][j]$ 表示第 $i$ 行選第 $j$ 個點，前 $i$ 行的最大值。
如果可以重復，那 DP 方程容易得出:
$f[i][j]=max_{1\le x\le m'}(f[i-1][x]+pre[i][x+k-1]-pre[i][x-1]) + pre[i][j+k-1] - pre[i][j-1]$, $pre[i]$ 是第 $i$ 行的前綴和。
前面一項容易維護，從而 $O(1)$ 轉移，總時間復雜度 $O(n^2)$。

考慮去掉重復貢獻。
設 $f[i][j]$ 表示第 $i$ 行選第 $j$ 個點，前 $i$ 行的最大值（不能重復貢獻）。
又設 $g[i][j]=f[i][j]+pre[i+1][j+k-1]-pre[i+1][j-1]$。
則轉移方程可以寫成：
$f[i][j]=max_{1\le x \le m'}{g[i-1][x]} + pre[i][j+k-1] - pre[i][j-1] - 重復貢獻的部分$。
考慮把重復貢獻的部分在 max 里就去掉，一個點 $a[i][y] (j\le y\le j+k-1)$ 重復貢獻在:
$g[i-1][y-k+1],...,g[i-1][y-1],g[i-1][y]$。
只需要把他們全部減去 $a[i][y]$ 即可，支持區(qū)間減，區(qū)間查最大值的是什么? 線段樹。轉移完之后再加回去。

但這樣是 $O(n \times m \times k \times \log m)$,因為要對每個 $j<=y<=j+k-1$ 都做一遍區(qū)間減。但是當 $j$ 從 $j$ 變到 $j+1$，其實只有 $j$ 這個位置不再被重復貢獻，$j+1+k-1$ 這個位置新加進來，所以就好了。
所以 $O(n\times m\times \log m)$。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=2e4+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,m,k,a[55][N],pre[55][N];
int f[55][N],g[N];
struct node{
	int l,r,maxn,add;
	void tag(int d){
		maxn+=d;
		add+=d;
	}
};
struct SegmentTree{
	node t[N<<2];
	void pushup(int p){
		t[p].maxn=max(t[p<<1].maxn,t[p<<1|1].maxn); 
	}
	void spread(int p){
		if(t[p].add){
			t[p<<1].tag(t[p].add);
			t[p<<1|1].tag(t[p].add);
			t[p].add=0;
		}
	}
	void build(int p,int l,int r){
		t[p].l=l,t[p].r=r,t[p].add=0;    //add也要清空 
		if(l==r){
			t[p].maxn=g[l];
			return;
		}	
		int mid=(l+r)>>1;
		build(p<<1,l,mid);
		build(p<<1|1,mid+1,r);
		pushup(p);
	} 
	void change(int p,int l,int r,int d){
		if(l<=t[p].l&&t[p].r<=r){
			t[p].tag(d);
			return;
		}
		spread(p);
		int mid=(t[p].l+t[p].r)>>1;
		if(l<=mid) change(p<<1,l,r,d);
		if(r>mid) change(p<<1|1,l,r,d);
		pushup(p);
	}
}Seg;

signed main(){
	n=read(),m=read(),k=read();
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			a[i][j]=read();
			pre[i][j]=pre[i][j-1]+a[i][j];
		}
	}
	
	int m1=m-k+1;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m1;j++){
			if(i!=1){
				if(j==1){
					for(int y=j;y<=j+k-1;y++) Seg.change(1,1,y,-a[i][y]);
				}
				else{
					Seg.change(1,max(1ll,j-1-k+1),j-1,a[i][j-1]);
					Seg.change(1,j,j+k-1,-a[i][j+k-1]);
				}
			}
			f[i][j]=Seg.t[1].maxn+pre[i][j+k-1]-pre[i][j-1];
			g[j]=f[i][j]+pre[i+1][j+k-1]-pre[i+1][j-1];
		}
		Seg.build(1,1,m1);
	}
	int ans=0;
	for(int i=1;i<=m1;i++) ans=max(ans,f[n][i]);
	printf("%lld\n",ans);
	return 0;
}

46.夏蟲（summer）

夏蟲（summer）

題意簡述:

用 $n$ 個蟲子，每個蟲子有一個狡猾值 $a_i$,一開始你會站在一個蟲子 $x$ 前，將初始能力值設為 $a_x$，并捕捉它，接下來你可以重復執(zhí)行三種操作，直到捕捉完所有昆蟲:
設當前捕捉到了區(qū)間 $[l,r]$ 的昆蟲，能力值為 $v$

若 $l \ne 1$ 并且 $a_{l?1} \le v$ ，那么可以花費 $1$ 單位精力捕捉 $l?1$ 號夏蟲；
若 $r \ne n$ 并且 $a_{r+1} \le v$ ，那么她們可以花費 $1$ 單位精力捕捉 $r + 1$ 號夏蟲；
花費 $k$ ($k$ 是定值)單位精力使得捕蟲網(wǎng)的能力值為 $min(a_{l?1}, a_{r+1})$。在這里定義 $a_0 = a_{n+1} = inf$。

有 $Q$ 次詢問，每次給定 $x,l,r$ 表示交換 $x,x+1$ 兩只昆蟲的位置后，詢問你初始站在 $[l,r]$ 內的每只昆蟲前的最小花費精力的和。注意交換操作是永久的，即會對后面的詢問產(chǎn)生影響。

題解:

首先操作 $1$ 和操作 $2$ 肯定加起來要做 $n-1$ 次，所以只需要看操作 $3$ 要幾次。
容易用單調棧維護處 $L[i]/R[i]$ 表示 $a[i]$ 作為最大值的區(qū)間。
那么設 $f[i]$ 表示以 $i$ 為開始需要多少次操作 $3$,不妨設 $a[L[i]-1] < a[R[i]+1]$,則 $f[i]=f[L[i]-1] + 1$。
所以按照值域從大到小 $dp$ 即可做到 $O(n)$ 求解單次詢問，那么時間復雜度 $O(nQ)$,有 40 分。

但是如果按照這種轉移的求法，不是很好在每次修改后維護 $f$,考慮換一個求法:
設 $A_x$ 表示 $a[1],a[2],...,a[x]$ 的后綴最大值的集合。$B_x$ 表示 $a[x],a[x+1],...,a[n]$ 的前綴最大值的集合。
那么答案就是 $|A_x \cup B_x| - 1$,-1 是因為 $a[x]$ 自己是不用算的，這個式子應該還好理解，就不證了。

我們維護兩棵線段樹 $Seg1,Seg2$。$Seg1$ 維護 $a$ 序列，$Seg2$ 維護 $f$ 。
注意:我們是無法去維護 $A,B$ 集合的，即不能對每個數(shù)開兩個 $multiset$，當然因為無法維護，我們也不需要真的在集合里刪掉某些數(shù)(這是好的)

假設現(xiàn)在交換了 $a[x],a[x+1]$,去考慮會影響哪些數(shù)的 $A,B$ 集合。

$a[x]<a[x+1]$

對于 $1 \le i \le x-1$ 的 $i$,它們的 $A$ 集合顯然是不變的，但是 $B$ 集合里有可能原來有 $a[x]$,現(xiàn)在就沒了(因為 $a[x+1]$ 跑到 $a[x]$ 前面了)。
首先我們需要知道哪些數(shù)的 $B$ 集合原來有 $a[x]$,容易知道一定是 $[l,x-1]$ 這一段區(qū)間的數(shù)，其中每個數(shù)都 $<a[x]$,注意如果 $=a[x]$ 是不算的，因為 $=a[x]$ 的話他的 $B$ 集合里仍然有 $a[x]$。
求這個 $l$ 在 $Seg1$ 上線段樹二分即可，但是要知道 $i \in [l,x-1]$ 的 $f[i]$ 是否改變還要看 $A[i]$ 里是否有 $a[x]$，這里不用也不能去每個數(shù)判斷一遍，注意到對于 $A[i]$,他在 $a[l],a[l+1],..,a[i]$ 的后綴$max$里肯定是沒有 $a[x]$ 的，所以只需要去看 $a[l-1]$ 是否 $=a[x]$ 即可。
如果 $a[l-1] \ne a[x]$的話他們的 $f[i]-1$,即在 $Seg2$ 上區(qū)間 $-1$。
對于 $i\ge x+2$,他們的 $B$ 集合不變，$A$ 集合要改變的是一段區(qū)間 $[x+2,r]$,他們都 $<a[x]$,它們的 $A$ 集合里會多出 $a[x]$。
同理求 $r$ 只需要線段樹二分。判斷 $f$ 是否要 $+1$ 只需要看 $a[r+1]$ 是否 $=a[x]$。
對于 $i=x,i=x+1$,注意到這個時候我已經(jīng)求出了其他 $i$ 的 $f$ 值，所以直接按照最初的 $f[i]=f[(L[i]-1) / (R[i]+1)] + 1$ 轉移即可,$L[i],R[i]$ 也可線段樹二分求。注意要按照從大到小的順序 DP

$a[x]>a[x+1]$ ,類似分類討論，不想寫了。

用上面的寫法是 $O(n + Qlogn)$ 但是因為不知道怎么寫這個線段樹二分，所以這邊想到了有兩種做法:

來自大佬 @RiceFruit 的: 在 $[l,r]$ 中查詢第一個滿足 $max(a[i],a[i+1],..,a[r]) \le val$ 的位置 $i$,就先把 $[l,r]$ 拆成 $log$ 個區(qū)間，然后先從后往前掃一遍判斷在哪一個子樹內，這樣對于一整個子樹的求解是好做的。
暴力二分用線段樹查詢的做法，所以是雙 $log$ 的。

一看就方法$2$好寫，所以一開始寫 $O(Q \times log^2n)$,但是這樣要跑 $1.6$s，~~當時看著自己TLE的 $8k$ 代碼人都炸了~~。
所以還是寫第一種吧。

代碼有億點點長,個人碼風問題，但真的感覺寫出來也是挺不容易的。
Swap函數(shù)那里碼風突變是因為不加空格看著太惡心了。

code

#include<bits/stdc++.h>
#define PII pair<int,int>
#define fi first
#define se second 
#define int long long 
using namespace std;
const int N=1e5+5,inf=1e18;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,k,T,a[N];
PII t[N];
int L[N],R[N],f[N];
stack<int> st;
struct node1{
	int l,r,maxn;
};
struct SegmentTree1{
	node1 t[N<<2];
	vector<int> v;  //存區(qū)間用 
	void pushup(int p){
		if(t[p<<1].maxn>t[p<<1|1].maxn) t[p].maxn=t[p<<1].maxn;
		else t[p].maxn=t[p<<1|1].maxn;
	}
	void build(int p,int l,int r){
		t[p].l=l,t[p].r=r;
		if(l==r){
			t[p].maxn=a[l];
			return;
		}
		int mid=(l+r)>>1;
		build(p<<1,l,mid);
		build(p<<1|1,mid+1,r);
		pushup(p);
	}
	int ask(int p,int l,int r){
		if(l<=t[p].l&&t[p].r<=r){
			return t[p].maxn;
		}
		int mid=(t[p].l+t[p].r)>>1,maxn=0;
		if(l<=mid) maxn=max(maxn,ask(p<<1,l,r));
		if(r>mid) maxn=max(maxn,ask(p<<1|1,l,r));
		return maxn;
	}
	void Get_range(int p,int l,int r){
		if(l<=t[p].l&&t[p].r<=r){
			v.push_back(p);
			return;
		}
		int mid=(t[p].l+t[p].r)>>1;
		if(l<=mid) Get_range(p<<1,l,r);
		if(r>mid) Get_range(p<<1|1,l,r);
	}
	int lower1(int p,int val,int op){
		if(t[p].l==t[p].r){
			if( (op==0&&t[p].maxn<val) || (op==1&&t[p].maxn<=val) ) return t[p].l;
			else return n+1; 
		}
		if( (op==0&&t[p<<1|1].maxn<val) || (op==1&&t[p<<1|1].maxn<=val) ) return min(lower1(p<<1,val,op) , t[p<<1|1].l);
		else return lower1(p<<1|1,val,op);
	}
	int lower2(int p,int val,int op){
		if(t[p].l==t[p].r){
			if( (op==0&&t[p].maxn<val) || (op==1&&t[p].maxn<=val) ) return t[p].l;
			else return 0; 
		}
		if( (op==0&&t[p<<1].maxn<val) || (op==1&&t[p<<1].maxn<=val) ) return max(t[p<<1].r , lower2(p<<1|1,val,op));
		else return lower2(p<<1,val,op);
	}
	int ask1(int l,int r,int val,int op){  //在 l~r 中查詢第一個滿足 max(a[i],a[i+1],..,a[r]) </<=  val 的位置 
		if(l>r) return n+1;
		if( (op==0&&a[r]>=val) || (op==1&&a[r]>val) ) return n+1;  //先保證有解 
		v.clear();  //子樹下標放這個里面,從左往右放 
		Get_range(1,l,r);
		int ans=r;
		for(int i=v.size()-1;i>=0;i--){
			int p=v[i];
			if( (op==0&&t[p].maxn<val) || (op==1&&t[p].maxn<=val) ) ans=min(ans,t[p].l);  //這里只需要比當前子樹的最大值就好了，掃過的那些已經(jīng)滿足了 
			else{
				ans=min(ans,lower1(p,val,op));
				break;
			}
		}
		return ans;
	}
	int ask2(int l,int r,int val,bool op){  //在 l~r 中查詢最后一個滿足 max(a[l],a[l+1],..,a[i]) </<=  val 的位置 
		if(l>r) return 0;
		if( (op==0&&a[l]>=val) || (op==1&&a[l]>val) ) return 0; 
		v.clear(); 
		Get_range(1,l,r);
		int ans=l;
		for(int i=0;i<v.size();i++){
			int p=v[i];
			if( (op==0&&t[p].maxn<val) || (op==1&&t[p].maxn<=val) ) ans=max(ans,t[p].r); 
			else{
				ans=max(ans,lower2(p,val,op));
				break;
			}
		}
		return ans;	
	}
	void change(int p,int x,int val){
		if(t[p].l==t[p].r){
			t[p].maxn=val;
			return;
		}
		int mid=(t[p].l+t[p].r)>>1;
		if(x<=mid) change(p<<1,x,val);
		else change(p<<1|1,x,val);
		pushup(p);
	}
}Seg1;
struct node2{
	int l,r,sum,add;
	void tag(int d){
		sum+=(r-l+1ll)*d,add+=d;
	}
};
struct SegmentTree2{
	node2 t[N<<2];
	void pushup(int p){
		t[p].sum=t[p<<1].sum+t[p<<1|1].sum;
	}
	void spread(int p){
		if(t[p].add){
			t[p<<1].tag(t[p].add);
			t[p<<1|1].tag(t[p].add);
			t[p].add=0;
		}
	}
	void build(int p,int l,int r){
		t[p].l=l,t[p].r=r;
		if(l==r){
			t[p].sum=f[l];
			return;
		}
		int mid=(l+r)>>1;
		build(p<<1,l,mid);
		build(p<<1|1,mid+1,r);
		pushup(p);
	}
	void change(int p,int x,int val){  
		if(t[p].l==t[p].r){
			t[p].sum=val;
			return;
		}
		spread(p);
		int mid=(t[p].l+t[p].r)>>1;
		if(x<=mid) change(p<<1,x,val);
		else change(p<<1|1,x,val);
		pushup(p);
	}
	void modify(int p,int l,int r,int d){  
		if(l<=t[p].l&&t[p].r<=r){
			t[p].tag(d);
			return;
		}
		spread(p);
		int mid=(t[p].l+t[p].r)>>1;
		if(l<=mid) modify(p<<1,l,r,d);
		if(r>mid) modify(p<<1|1,l,r,d);
		pushup(p);	
	}
	int ask(int p,int l,int r){
		if(l<=t[p].l&&t[p].r<=r){
			return t[p].sum;
		}
		spread(p);
		int mid=(t[p].l+t[p].r)>>1,res=0;
		if(l<=mid) res+=ask(p<<1,l,r);
		if(r>mid) res+=ask(p<<1|1,l,r);
		return res;
	}
	int ask2(int p,int x){
		if(t[p].l==t[p].r) return t[p].sum;
		spread(p);
		int mid=(t[p].l+t[p].r)>>1;
		if(x<=mid) return ask2(p<<1,x);
		else return ask2(p<<1|1,x);
	}
}Seg2;
void Init(){
	st.push(0);
	for(int i=1;i<=n;i++){
		while(st.size()&&a[st.top()]<=a[i]) st.pop();
		L[i]=st.top()+1ll;
		st.push(i);
	}
	while(st.size()) st.pop();
	st.push(n+1);
	for(int i=n;i>=1;i--){
		while(st.size()&&a[st.top()]<=a[i]) st.pop();
		R[i]=st.top()-1ll;
		st.push(i);
	}	
	
	f[0]=f[n+1]=-1ll;
	sort(t+1,t+n+1,[](PII x,PII y){return x.fi>y.fi;});
	for(int i=1;i<=n;i++){
		if(a[L[t[i].se]-1] < a[R[t[i].se]+1]) f[t[i].se]=f[L[t[i].se]-1]+1ll;
		else f[t[i].se]=f[R[t[i].se]+1]+1ll;
	}
	
	Seg1.build(1,0,n+1);
	Seg2.build(1,0,n+1);     //雖然查不到 0/n+1 但是可能要用 
}
void Swap(int x){
	if(a[x]==a[x+1]) return;
	if(a[x]<a[x+1]){
		int l = Seg1.ask1(1 , x-1 , a[x] , 0);
		if(l<=x-1 && a[l-1] != a[x]) Seg2.modify(1 , l , x-1 , -1ll);
		
		int r=Seg1.ask2(x+2 , n , a[x] , 0);
		if(r>=x+2 && a[r+1] != a[x]) Seg2.modify(1 , x+2 , r , 1ll);
		
		Seg1.change(1 , x , a[x+1]) , Seg1.change(1 , x+1 , a[x]);  
		int maxn=a[x+1],ming=a[x]; 
		swap(a[x],a[x+1]);  
		//先更新大的再更新小的 
		int L1 = Seg1.ask1(1 , x , maxn , 1) , R1 = Seg1.ask2(x , n , maxn , 1) , F;  //注意這個時候 a[x+1] 在 x 的位置
		if( a[L1-1] < a[R1+1] ) F = Seg2.ask2(1 , L1-1) + 1ll;
		else F = Seg2.ask2(1 , R1+1) + 1ll;
		Seg2.change(1 , x , F);
		L1 = Seg1.ask1(1 , x+1 , ming , 1) , R1 = Seg1.ask2(x+1 , n , ming , 1) , F;  //注意這個時候 a[x] 在 x+1 的位置
		if( a[L1-1] < a[R1+1] ) F = Seg2.ask2(1 , L1-1) + 1ll;
		else F = Seg2.ask2(1,R1+1) + 1ll;
		Seg2.change(1 , x+1 , F);
		
	}
	else{  //a[x]>a[x+1]
		int l = Seg1.ask1(1 , x-1 , a[x+1] , 0);   //此時可能多出來一個 a[x+1] 
		if(l<=x-1 && a[l-1] != a[x+1]) Seg2.modify(1 , l , x-1 , 1ll);
		
		int r = Seg1.ask2(x+2 , n , a[x+1] , 0);
		if(r>=x+2 && a[r+1] != a[x+1]) Seg2.modify(1 , x+2 , r , -1ll);
		
		Seg1.change(1 , x ,a[x+1]) , Seg1.change(1 , x+1 , a[x]); 
		int maxn=a[x],ming=a[x+1];
		swap(a[x],a[x+1]);  		
		int L1 = Seg1.ask1(1 , x+1 , maxn , 1) , R1 = Seg1.ask2(x+1 , n , maxn , 1) , F;  
		if( a[L1-1] < a[R1+1] ) F = Seg2.ask2(1 , L1-1) + 1ll;
		else F = Seg2.ask2(1 , R1+1) + 1ll;
		Seg2.change(1 , x+1 , F);
		L1 = Seg1.ask1(1 , x , ming , 1) , R1 = Seg1.ask2(x , n , ming , 1) , F; 
		if( a[L1-1] < a[R1+1] ) F = Seg2.ask2(1 , L1-1) + 1ll;
		else F = Seg2.ask2(1 , R1+1) + 1ll;
		Seg2.change(1 , x , F);
		
	}
}
signed main(){
	freopen("summer.in","r",stdin);
	freopen("summer.out","w",stdout);
	n=read(),k=read();
	for(int i=1;i<=n;i++) a[i]=read(),t[i].fi=a[i],t[i].se=i; 
	a[0]=a[n+1]=inf;
	Init();
	T=read();
	while(T--){
		int x=read(),l=read(),r=read();
		Swap(x);
		printf("%lld\n",Seg2.ask(1,l,r)*k + (n-1)*(r-l+1));
	}
	return 0;
}

47.任務安排

任務安排

弱化版是不用斜率優(yōu)化的。
設 $f[i][j]$ 表示前 $i$ 個任務分成 $j$ 段的最小花費。
$f[i][j]=min_{0\le j \le i-1}(f[k][j-1] + s + (S1[i]+s\times j)\times (S2[i]-S2[k]))$。
$S1$ 是 $t$ 的前綴和,$S2$ 是 $F$ 的前綴和。
這樣是 $O(n^3)$ 的。

回顧"我的動態(tài)規(guī)劃題單2"中"關路燈"那題，
考慮將 $s$ 的費用提前計算，只考慮當前這批任務對后面的影響，這樣就可以不去記錄段數(shù) $j$ 了。
$f[i]=min_{0\le j \le i-1}(f[j] + S1[i]\times(S2[i]-S2[j]) + s\times (S2[n]-S2[j]))$。

時間復雜度$O(n^2)$。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=1e5+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,s,t[N],F[N],f[N],S1[N],S2[N];
signed main(){
	n=read(),s=read();
	for(int i=1;i<=n;i++){
		t[i]=read(),F[i]=read();	
		S1[i]=S1[i-1]+t[i];
		S2[i]=S2[i-1]+F[i];
	} 
	memset(f,0x3f,sizeof f);
	f[0]=0;
	for(int i=1;i<=n;i++){
		for(int j=0;j<i;j++){
			f[i]=min(f[i],f[j] + S1[i]*(S2[i]-S2[j]) + s*(S2[n]-S2[j]));   
		}
	}
	printf("%lld\n",f[n]);
	return 0;
}

48.任務安排2

任務安排2

$f[i]=min_{0\le j \le i-1}(f[j] + S1[i]\times(S2[i]-S2[j]) + s\times (S2[n]-S2[j]))$。

按照dp的套路，把式子改寫一下，只跟 $j$ 有關和只跟 $i$ 有關的拎出來:
$f[i]=min_{0\le j \le i-1}(f[j] - (s+S1[i])\times S2[j]) + s\times S2[n] + S1[i]\times S2[i]$。
不管后面那一坨，去掉 $min$ 寫成 $y=kx+b$ 的形式:
$(s+S1[i])\times S2[j] + f[i] = f[j]$。
所以就用一條斜率為 $(s+S1[i])$ 的直線去切這些形如 $(S2[j] , f[j])$ 的點。
維護出下凸殼之后，注意到因為 $t_i$ 都是正數(shù)，所以斜率 $(s+S1[i])$ 隨著 $i$ 的增大而增大，那根據(jù)切點的判定條件，切點也是一定右移的，所以只保留斜率大于 $(s+S1[i])$ 的部分即可。
而且注意到這里的 $L(i)$ 函數(shù)始終是 $0$，所以就有了一下 O(n) 的做法:

用單調隊列替換掉單調棧。
對于 $i$,把隊頭那些斜率 $\le (s+S1[i])$ 的線段 pop 掉，這樣隊頭的點就是要求的切點。
取出隊頭轉移。
加入 $i$,并維護下凸殼。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=3e5+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,s,t[N],c[N],f[N],S1[N],S2[N];
int dq[N],l,r;  //單調隊列 
int x(int j){return S2[j];}  //橫坐標
int y(int j){return f[j];}  //縱坐標 
signed main(){
	n=read(),s=read();
	for(int i=1;i<=n;i++){
		t[i]=read(),c[i]=read();	
		S1[i]=S1[i-1]+t[i];
		S2[i]=S2[i-1]+c[i];
	}
	memset(f,0x3f,sizeof f);
	f[0]=0;
	l=1,r=0; //初始化空的單調隊列 
	dq[++r]=0;
	for(int i=1;i<=n;i++){
		while( l<r && ( y(dq[l+1]) - y(dq[l]) ) <= (s + S1[i]) * ( x(dq[l+1]) - x(dq[l]) ) ) l++;    //注意是 l<r 而不是 l<=r,因為起碼要有兩個點才是線段 
		int j=dq[l];
		f[i]=f[j] + S1[i]*(S2[i]-S2[j]) + s*(S2[n]-S2[j]);  //這里就用原來的式子就好了,新的那個太大便了 
		while( l<r && ( y(dq[r]) - y(dq[r-1]) ) * ( x(i) - x(dq[r]) ) >= ( y(i) - y(dq[r]) ) * ( x(dq[r]) - x(dq[r-1]) ) ) r--;    //維護凸殼 
		dq[++r]=i;
	}
	
	printf("%lld\n",f[n]);
	return 0;
}

49.[SDOI2012] 任務安排

[SDOI2012] 任務安排

題面都是一樣的。

這里 $t_i$ 可能是負數(shù)，所以 $(s+S1[i])$ 不一定單調。
所以求切點要二分，這里還是用的單調隊列，其實單調棧也可以。
時間復雜度 O(n log n)。
要注意的是，這里 $c_i$ 可以等于 $0$,也就是說也就是會出現(xiàn)橫坐標相同的兩個點，那么有可能出現(xiàn)原先的斜率是 $inf$(即與 $x$ 軸垂直，但是后面那個在前面那個上面)，加進來一個后變成 $-inf$(加進來的在原來隊尾的下面)，但它們的斜率在比較時是一樣，如果不把前面那個彈掉，就不滿足斜率單調遞增了，所以在維護下凸殼時，$=$ 的情況也要把隊尾彈掉(代碼中也有注釋）。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=3e5+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,s,t[N],c[N],f[N],S1[N],S2[N];
int dq[N],l,r;  //單調隊列 
int x(int j){return S2[j];}  //橫坐標
int y(int j){return f[j];}  //縱坐標 
int Binary_search(int K){
	int L=l,R=r,mid,res=r;  //二分找第一個滿足它后面的線段的斜率比 s+S1[i] 大的點y 
	while(L<=R){
		mid=(L+R)>>1;
		if(mid<r && y(dq[mid+1]) - y(dq[mid]) > K * ( x(dq[mid+1]) - x(dq[mid]) )) R=mid-1,res=mid;
		else L=mid+1;
	}
	return dq[res];
}
signed main(){
	n=read(),s=read();
	for(int i=1;i<=n;i++){
		t[i]=read(),c[i]=read();	
		S1[i]=S1[i-1]+t[i];
		S2[i]=S2[i-1]+c[i];
	}
	memset(f,0x3f,sizeof f);
	f[0]=0;
	l=1,r=0; //初始化空的單調隊列 
	dq[++r]=0;
	for(int i=1;i<=n;i++){
		int j=Binary_search(s+S1[i]);
		f[i]=f[j] + S1[i]*(S2[i]-S2[j]) + s*(S2[n]-S2[j]); 
		while( l<r && ( y(dq[r]) - y(dq[r-1]) ) * ( x(i) - x(dq[r]) ) >= ( y(i) - y(dq[r]) ) * ( x(dq[r]) - x(dq[r-1]) ) ) r--;    //維護凸殼 
		/*
			這邊取等號是因為 ti 可以=0，也就是會出現(xiàn)橫坐標相同的兩個點，那么有可能出現(xiàn)原先的斜率是 inf(即與 x 軸垂直，但是后面那個在前面那個上面)，
			加進來一個后變成 -inf，但它們的斜率表示出來是一樣，如果不把前面那個彈掉，就不滿足斜率單調遞增了。 
		*/ 
		dq[++r]=i;
	}
	
	printf("%lld\n",f[n]);
	return 0;
}

50.忘情

忘情

不會斜率優(yōu)化的戳這里。
不會wqs二分的戳這里。

把式子變成 $((\sum_{i=1}^n x_i)+1)^2 $,設 $S$ 為前綴和，那么樸素的 dp 是:
設 $f[i][j]$ 表示前 $i$ 個數(shù)劃分成 $j$ 段的最小值，轉移為 $f[i][j]=\min_{0<=k<i}(f[k][j-1] + (S_i - S_j + 1)^2)$。
容易證明 $(a+b+1)^2 > (a+1)^2 + (b+1)^2$,也就是說分的段數(shù)越多答案越小，即按照上面的定義 $g(x)$ 表示分 $x$ 段的最小值，那么 $g(x)$ 的圖像應該是一個下凸殼:

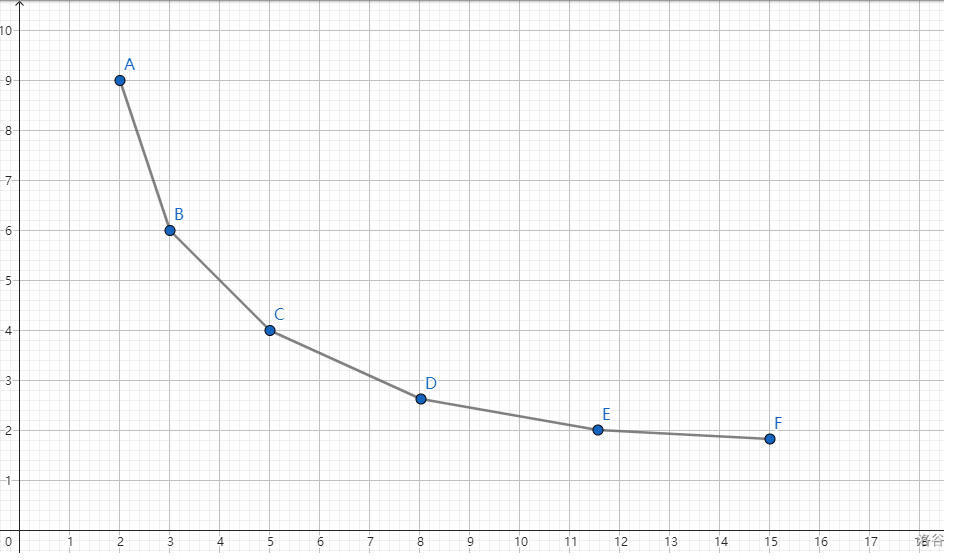
二分一個斜率 $K$,用斜率 $K$ 的直線去切這個凸包，那么截距 $b=h(x)=g(x)-Kx$,因為是下凸包，所以我們要求最小截距，即把一段的權值定義成 $((\sum xi)+1)^2 - K$,然后去掉段數(shù)限制，求最小答案。
考慮對這個新的問題 $dp$,設 $dp[i]$ 表示前 $i$ 個數(shù)的最小值,$dp[i]=\min_{0<=j<i}(dp[j] + (S[i]-S[j]+1)^2 - K)$,因為還要求此時的橫坐標 $x$，所以還要額外記一個dp數(shù)組，轉移也是顯然的。
這是經(jīng)典的斜率優(yōu)化形式，可以用單調隊列優(yōu)化到 $O(n)$。
總時間復雜度 $O(n \log n)$。

wqs 二分一些實現(xiàn)的細節(jié)：

這里因為是下凸包，所以斜率 $K$ 是負的，但是為了方便二分時我們把他變成正的，所以 check 里 dp 變成 $dp[i]=\min_{0<=j<i}(dp[j] + (S[i]-S[j]+1)^2 + K)$ , 原來二分要把斜率調大的就調小。
注意最后凸包可能會有一段斜率為 $0$ 的線段，即可能 $g(m-1)=g(m)$，那如果我們在 $check$ 里的斜率優(yōu)化dp,在 $g$ 值相同時取的是靠左的點，那么二分寫的就是: 如果返回的那個 $x$ <=m,那就更新答案并把斜率調大(這里還認為斜率是負的，不進行 1. 的轉換) ; 相反，如果我們在 $check$ 里的斜率優(yōu)化dp,在 $g$ 值相同時取的是靠右的點，那么二分寫的就是: 如果返回的那個 $x$ >=m,那就更新答案并把斜率調小。看取的是靠左還是靠右只要看斜率優(yōu)化維護凸包時寫的是 >= 還是 >,> 就是取靠左的，>=就是取靠右的。

code

變量名稍有不同。

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=1e5+5,inf=1e18;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}

int n,m,a[N]; 
int dp[N],g[N];  //dp[i]表示前 i 個數(shù)分成若干段的最小值，g[i] 表示取到最小值分的段樹 
int dq[N],l,r;
int calc(int j){  //求縱坐標 
	return dp[j]+a[j]*a[j]-2ll*a[j];
} 
void check(int mid){
	l=1,r=0;
	dp[0]=0,g[0]=0;   
	dq[++r]=0;  //放 0 不是 1，因為可以自成 1 段。 
	for(int i=1;i<=n;i++){
		while(l<r && ( calc(dq[l+1]) - calc(dq[l]) ) < (2ll * a[i] * (a[dq[l+1]] - a[dq[l]]))) l++;  //把開頭斜率小于當前斜率的線段 pop 掉
		int j=dq[l];
		dp[i]=dp[j]+(a[i]-a[j]+1ll)*(a[i]-a[j]+1ll)+mid;
		g[i]=g[j]+1ll;
		while(l<r && ( calc(i) - calc(dq[r]) ) * ( a[dq[r]] - a[dq[r-1]]) < ( calc(dq[r]) - calc(dq[r-1] ) ) * ( a[i] - a[dq[r]] )) r--;  //維護凸殼
		dq[++r]=i; 
	}
}
signed main(){
	n=read(),m=read();
	for(int i=1;i<=n;i++) a[i]=read(),a[i]+=a[i-1];
	int l=0,r=inf,mid,ans=0;   //實際上斜率是負的，但是移項之后:b=f(x)-kx,所以就干脆把 k 取成正的，這樣在check里是每一段+mid,而不是-mid 
	while(l<=r){
		mid=(l+r)>>1;
		check(mid);
		if(g[n]<=m) r=mid-1,ans=mid;
		else l=mid+1; 
	}
	check(ans);
	printf("%lld\n",dp[n]-ans*m);  //這里要減掉 mid(也就是最后的 ans) 帶來的貢獻 
	return 0;
}

51.CF229D Towers

CF229D Towers

題意簡化:
把一個序列分成若干段，使每一段的和非嚴格單增,求合并的最小操作數(shù)。

$f[i]$ 表示前 $i$ 個數(shù)的最少操作數(shù),$g[i]$ 表示此時最后一段的和。
下面 $pre$ 表示前綴和。

容易發(fā)現(xiàn)最后一段的和越少越好，則
$f[i]_{0<=j<i，g[j]<=pre[i]-pre[j]}=f[j]+i-j-1 $, 即把 $[j+1,i]$ 分為一段,最后一個滿足條件的 $j$ 就是我們要的，因為此時最后一段的和 $pre[i]-pre[j]$ 最小。

這個紫題是不是有點水了。

code

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,a[N],f[N],g[N]; 
signed main(){
	n=read();
	for(int i=1;i<=n;i++) a[i]=read(),a[i]+=a[i-1];
	f[0]=0,g[0]=0;
	for(int i=1;i<=n;i++){
		for(int j=i-1;j>=0;j--){
			if(g[j]<=a[i]-a[j]){
				f[i]=f[j]+i-j-1;
				g[i]=a[i]-a[j];
				break;
			}
		}
	}
	printf("%d\n",f[n]);
	return 0;
}

52.【模板】"動態(tài) DP"&動態(tài)樹分治

【模板】"動態(tài) DP"&動態(tài)樹分治

也可見博客DP優(yōu)化——動態(tài)dp。

這道題是簡單版。

簡單版的前置知識:樹鏈剖分，廣義矩陣乘法。

不帶修改的話，最大權獨立集很簡單:
$f[u][0] = \sum _{v\in son(u)}max(f[v][0],f[v][1])$，表示不選 u 的答案。
$f[u][1] = w[u] + \sum _{v\in son(u)}f[v][0]$，表示選 u 的答案。

注意到我們更改一個點的點權其實只會修改他到根的鏈上的那些 $dp$ 值，所以全部重算一點都不劃算。
考慮只去更改這條鏈上的dp值。
但這樣當樹是鏈時還是有可能 TLE (雖然題解區(qū)似乎有人 $n$ 方過百萬)，這個時候就會想到樹鏈剖分。
因為根到一個點最多會有 log 個不同的重鏈，所以可以考慮重鏈之間暴力修改，重鏈上用線段樹快速維護。

這樣的話我們就需要更改一下 $f$ 的轉移，使得能與樹剖的性質匹配($f$ 的定義不變)。
設 $g[u][0/1]$ 表述 $u$ 選/不選，只考慮 $u$ 的那些輕兒子，的答案。
那么 ($son[u]$ 表示 $u$ 的重兒子):
$f[u][0] = g[u][0] + max(f[son[u][0],f[son[u][1])$
$f[u][1] = g[u][1] + f[son[u]][0]$。
特別的，葉子結點的 $g[u][0]=0,g[u][1]=w[u]$ (和他的 f 相同)。

因為沒了討厭的 $∑$，這個轉移我們嘗試改寫成矩陣(為了后面用線段樹維護)。
$f[u][0] = max(g[u][0]+f[son[u][0] , g[u][0]+f[son[u]][1])$
$f[u][1] = g[u][1] + f[son[u]][0]$。
根據(jù)這個可以得到他的 $(+,\max)$ 廣義矩陣乘法形式。

\[\begin{pmatrix} f[son[u]][0] & f[son[u]][1] \\ \end{pmatrix} \times \begin{pmatrix} g[u][0] & g[u][1] \\ g[u][0] & -inf \\ \end{pmatrix} = \begin{pmatrix} f[u][0] & f[u][1] \end{pmatrix} \]

會得到轉移矩陣里只跟當前點的 $g$ 有關。
注意到轉移時我們只需要重兒子的信息，以及當前點的 $g$ 值，所以我們在線段樹上維護每個點的 $g$ 所構成的轉移矩陣以及矩陣的區(qū)間乘積。
又注意到一條重鏈的底部一定是葉子。
所以對于一條重鏈的頂端他的 $f$ 值就是這條重鏈的每個轉移矩陣的乘積再乘一個初始矩陣(就是葉子的 $f$ 值)，這個區(qū)間乘線段樹是好維護的。
所以我們只維護 $g$ (或者其實是轉移矩陣)就可以了。

修改流程如下:

當修改一個點 $u$ 的點權時,當前點的 $g[u][1]$ 要變一下。
然后 $u$ 到 $top[u](重鏈頂端)$ 的所有點的 $g$ 都是不變的,因為 $g$ 在計算時不包含重兒子。
當 $top[u]$ 跳到 $fa[top[u]]$ 時，這時因為 $top[u]$ 是 $fa[top[u]]$ 的輕兒子，所以要更改 $fa[top[u]]$ 的 $g$ 值。
算 $fa[top[u]$ 的 $g$ 值要用到 $top[u]$ 的 $f$ 值，所以這個時候需要在線段樹上區(qū)間查詢一下。

復雜度是 $O(n\times log^2(n))$，因為修改時要跳 $log$ 次，每跳一次都要在線段樹上查詢一次。

一些細節(jié):
矩陣乘法不滿足交換律!!!所以線段樹上 pushup 要從后往前合并。

code

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,T,w[N];
int tot,head[N],to[N<<1],Next[N<<1];
void add(int u,int v){
	to[++tot]=v,Next[tot]=head[u],head[u]=tot;
}

int top[N],down[N],rev[N],dfn[N],fa[N],son[N],Size[N],num,g[N][2],f[N][2];
//down是重鏈底端 
void dfs1(int u){
	Size[u]=1;
	for(int i=head[u];i;i=Next[i]){
		int v=to[i];
		if(v==fa[u]) continue;
		fa[v]=u;
		dfs1(v);
		Size[u]+=Size[v];
		if(Size[v]>Size[son[u]]) son[u]=v;
	}
}
void dfs2(int u){
	dfn[u]=++num;
	rev[num]=u;
	if(son[fa[u]]==u) top[u]=top[fa[u]];
	else top[u]=u;
	if(son[u]) dfs2(son[u]),down[u]=down[son[u]];
	else down[u]=u;
	g[u][1]=w[u];
	for(int i=head[u];i;i=Next[i]){
		int v=to[i];
		if(v==fa[u]||v==son[u]) continue;
		dfs2(v);
		g[u][0]+=max(f[v][0],f[v][1]);
		g[u][1]+=f[v][0];
	}
	f[u][0]=g[u][0]+max(f[son[u]][0],f[son[u]][1]);
	f[u][1]=g[u][1]+f[son[u]][0];
} 

struct Matrix{
	int n,m,a[3][3];
	void Init(){memset(a,-0x3f,sizeof a);}
	void Init2(){ //單位矩陣 
		for(int i=1;i<=n;i++){
			for(int j=1;j<=m;j++){
				if(i==j) a[i][j]=0;
				else a[i][j]=-0x3f3f3f3f;
			}
		}
	}
}F;
Matrix operator *(Matrix A,Matrix B){
	Matrix C; C.Init();
	C.n=A.n,C.m=B.m;
	for(int i=1;i<=C.n;i++){
		for(int j=1;j<=C.m;j++){
			for(int k=1;k<=A.m;k++){
				C.a[i][j]=max(C.a[i][j],A.a[i][k]+B.a[k][j]);
			}
		}
	}
	return C;
}

struct node{
	int l,r;
	Matrix G;
};
struct SegmentTree{
	node t[N<<2];
	void pushup(int p){
		t[p].G=t[p<<1|1].G*t[p<<1].G;
	}
	void build(int p,int l,int r){
		t[p].l=l,t[p].r=r;
		if(l==r){
			t[p].G.n=2,t[p].G.m=2;
			int u=rev[l];
			t[p].G.a[1][1]=g[u][0],t[p].G.a[1][2]=g[u][1],t[p].G.a[2][1]=g[u][0],t[p].G.a[2][2]=-0x3f3f3f3f;
			return;
		}
		int mid=(l+r)>>1;
		build(p<<1,l,mid);
		build(p<<1|1,mid+1,r);
		pushup(p);
	}
	void change(int p,int x){
		if(t[p].l==t[p].r){
			int u=rev[x];
			t[p].G.a[1][1]=g[u][0],t[p].G.a[1][2]=g[u][1],t[p].G.a[2][1]=g[u][0],t[p].G.a[2][2]=-0x3f3f3f3f;
			return;
		}
		int mid=(t[p].l+t[p].r)>>1;
		if(x<=mid) change(p<<1,x);
		else change(p<<1|1,x);
		pushup(p);
	}
	Matrix ask(int p,int l,int r){
		if(l<=t[p].l&&t[p].r<=r) return t[p].G;
		int mid=(t[p].l+t[p].r)>>1;
		Matrix Res; Res.n=2,Res.m=2,Res.Init2();
		if(r>mid) Res=Res*ask(p<<1|1,l,r);
		if(l<=mid) Res=Res*ask(p<<1,l,r);
		return Res;
	}
}Seg;
void Init(){ //預處理:樹剖,g 數(shù)組,f 數(shù)組,初始化線段樹 
	dfs1(1); 
	dfs2(1);  
	
	Seg.build(1,1,n);
	F.n=1,F.m=2;
	F.a[1][1]=0,F.a[1][2]=-0x3f3f3f3f;  //初始矩陣，F(xiàn) 乘以葉子的轉移矩陣就是葉子的 f。 
}
void change(int x,int y){
	int tmp=x;
	x=top[x];
	while(x!=1){   //先算出涉及到的點原來的 f 
		Matrix Ans=F;
		Ans=Ans * Seg.ask(1,dfn[x],dfn[down[x]]);
		f[x][0]=Ans.a[1][1],f[x][1]=Ans.a[1][2];
		g[ fa[x] ][0] -= max(f[x][0],f[x][1]);
		g[ fa[x] ][1] -= f[x][0];
		x=top[fa[x]];
	}

	x=tmp;
	g[x][1]-=w[x] , w[x]=y , g[x][1]+=w[x];
	Seg.change(1,dfn[x]);
	x=top[x];
	while(x!=1){
		Matrix Ans=F;
		Ans=Ans * Seg.ask(1,dfn[x],dfn[down[x]]);
		f[x][0]=Ans.a[1][1],f[x][1]=Ans.a[1][2];
		g[ fa[x] ][0] += max(f[x][0],f[x][1]);
		g[ fa[x] ][1] += f[x][0];
		Seg.change(1,dfn[fa[x]]);
		x=top[fa[x]];
	} 
	
}
signed main(){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	n=read(),T=read();
	for(int i=1;i<=n;i++) w[i]=read();
	for(int i=1;i<n;i++){
		int u=read(),v=read();
		add(u,v),add(v,u);
	}
	
	Init();
	
	while(T--){
		int x=read(),y=read();
		change(x,y);
		Matrix Ans=F;
		Ans=Ans * Seg.ask(1,dfn[1],dfn[down[1]]);
		printf("%d\n",max(Ans.a[1][1],Ans.a[1][2]));
	}
	return 0;
}

53.【模板】"動態(tài)DP"&動態(tài)樹分治（加強版）

【模板】"動態(tài)DP"&動態(tài)樹分治（加強版）

把樹剖卡掉了。

那有什么別的辦法呢？
于是就誕生了這個非常厲害的科技——全局平衡二叉樹。

請確保先會了簡單版的樹剖 + 線段樹寫法。

思考樹剖為什么需要兩個 $\log$，因為我們每往上跳一次就要做一次 $O(\log n)$ 的區(qū)間查詢，然后我們一共要跳 $\log$ 次，所以是兩個 $\log$。
考慮把一個 $\log$ 去掉，跳 $\log$ 次重鏈的這個 $\log$ 肯定是去不掉了，只能去掉那個查詢的 $\log$。
但是很難有一個數(shù)據(jù)結構能 $O(1)$ 維護一個比較復雜的且?guī)薜膮^(qū)間信息。
所以全局平衡二叉樹的主要思路就是使樹高直接變成 $\log$，然后每一次真的直接往上一步步跳，而不是跳一條重鏈，在跳的過程中上傳信息并合并（這個容易做到 $O(1)$），這樣每次跳都是 $O(1)$ 的了。

怎么建樹呢?

首先全局平衡二叉樹先對每條重鏈建了一個平衡二叉樹，每條重鏈的建法是：

先一遍 dfs 維護出基本信息 $Size$ 表示子樹大小,$son$ 表示重兒子，$lsiz$ 表示除去重兒子所在子樹的子樹大小。
然后對每條重鏈弄一個類似點分治的過程，把這條鏈搞到一段序列上，每次找出以 $lsiz$ 為權值的帶權中點 $rt$；
以 $rt$ 為平衡二叉樹的根，然后左右分別遞歸建樹并把左右兩邊得到的根設為 $rt$ 的左右兒子。

然后把一個點用輕邊連接的兒子對應的平衡二叉樹的根接到這個點對應的平衡二叉樹的根下面。

舉個例子，比如這個圖：

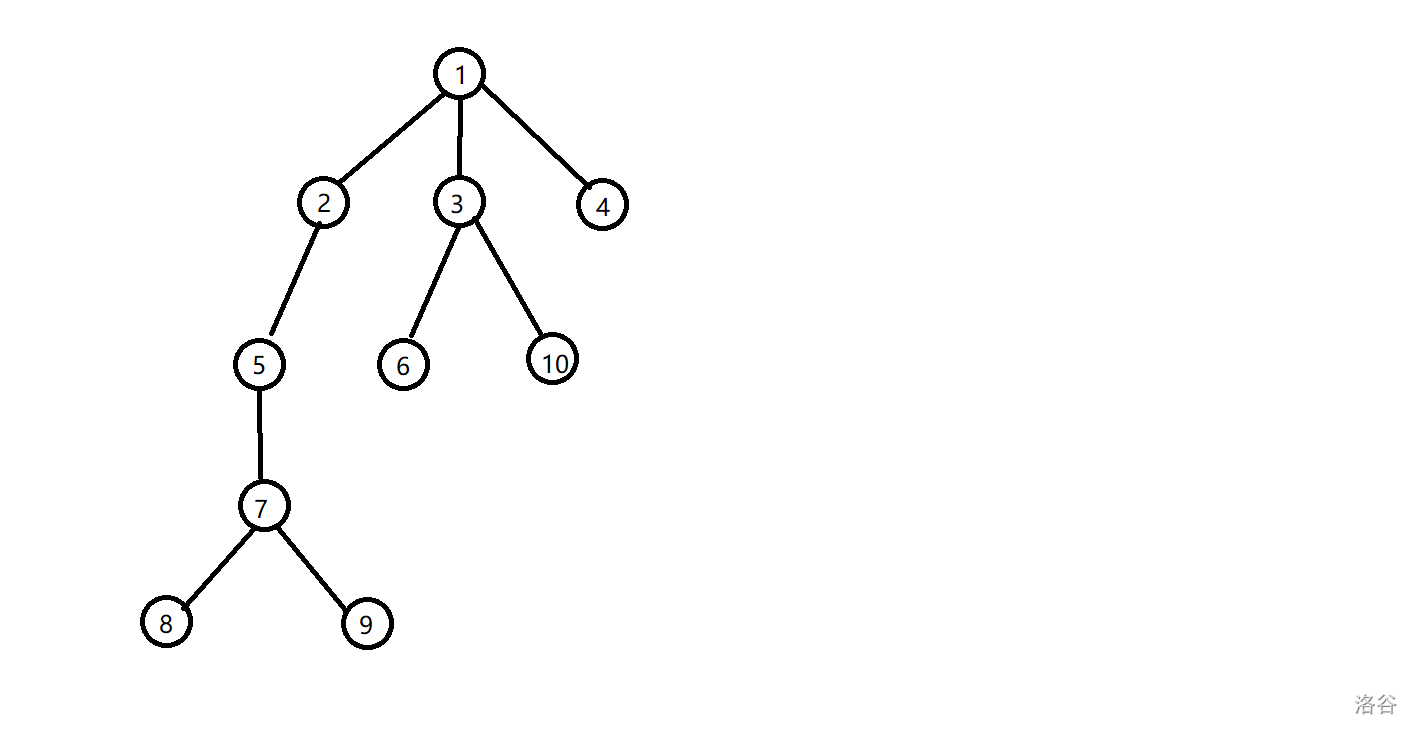
他的重鏈以及 $lsiz$ 如下圖所示：

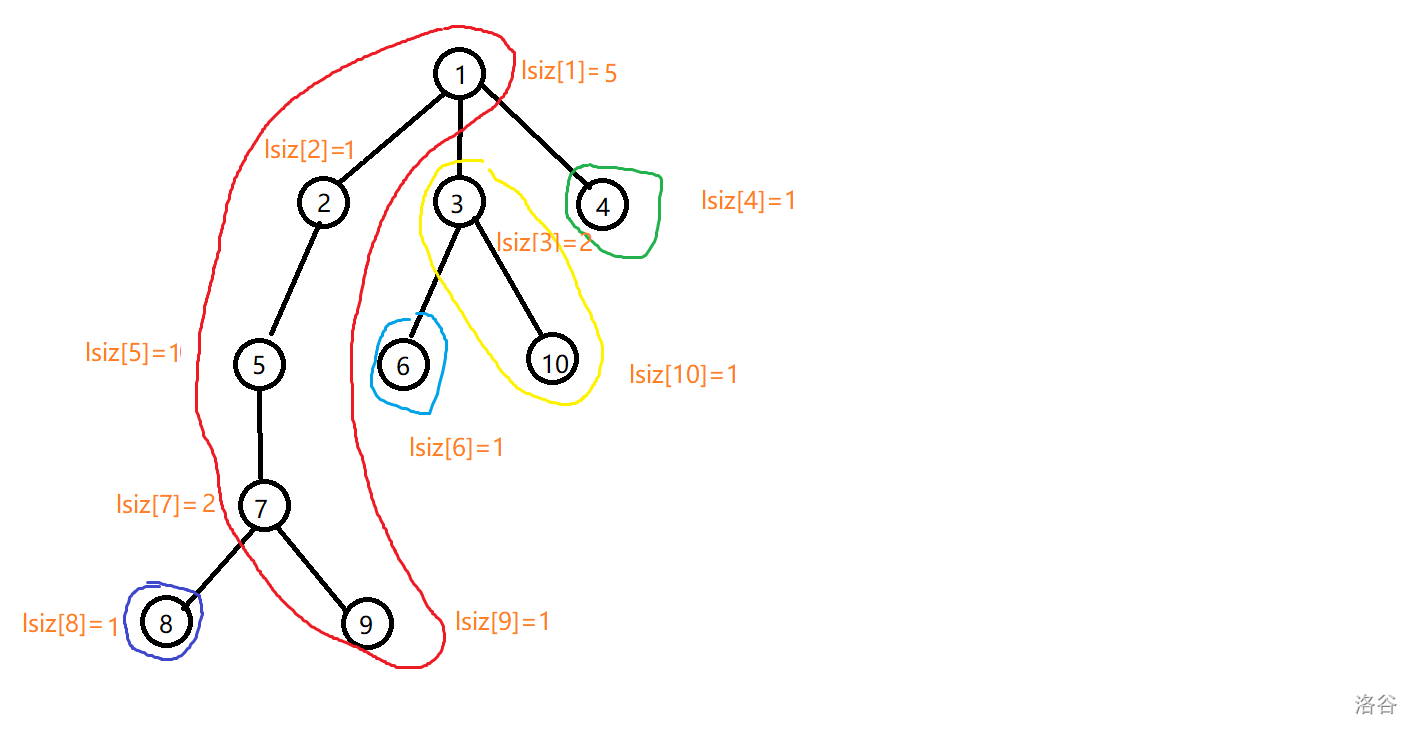
那么他建出的全局平衡二叉樹應該長這樣子，不同顏色代表不同重鏈建出的平衡二叉樹，虛線邊代表連接這些二叉樹的邊:

Tip：所以可以看出全局平衡二叉樹并不是一棵二叉樹，而是一個二叉樹森林連接起來得到的一棵多叉樹。

思路就是這么個思路，代碼實現(xiàn)時：
遞歸建樹，當 build 到一個點 $u$ 時，先拉出重鏈，
然后對重鏈上的每個點先去遞歸它的輕兒子并把返回的根接到那個點上(對于輕邊我們只記錄父親而不記錄兒子)。
對于一條重鏈再按照上面所說的方法去特殊地建樹，
并維護出這個重鏈的所有轉移矩陣的乘積,只要每次 pushup 即可,還是記得注意順序，因為矩陣乘法沒有交換律。

到此全局平衡二叉樹就建完了。

全局平衡二叉樹的每個點維護了兩個信息，自己這個點本身的轉移矩陣 $matr1$，他所代表的重鏈上的區(qū)間的轉移矩陣的乘積 $matr2$。
修改時，我們從修改的點開始，先改掉它對應的轉移矩陣 $matr1$ (此時先不要 pushup 更改自身的 $matr2$，因為后面需要用到舊的 $matr2$)。
然后在全局平衡二叉樹上一步一步往上跳，假設當前在 $u$ 點，全局平衡二叉樹上的父親為 $fa$:

如果 $(u,fa)$ 這條邊是重邊就直接 pushup(u) 把 $u$ 的 $matr2$ 改掉，先不用修改 $fa$ 的 $matr2$;
如果 $(u,fa)$ 這條邊是輕邊，此時 $u$ 的 $matr2$ 是舊版本，可以很快的求出 $u$ 原先的 $f$ 值，把 $fa$ 的轉移矩陣 $matr1$ 減掉舊的 $f$ 值；再 pushup(u) ,算出新的 $f$ 值，把 $fa$ 的轉移矩陣 $matr1$ 加上新的 $f$ 值。

查詢時，如果查詢根的話，直接查詢根所在重鏈的轉移矩陣的乘積即可。
查詢子樹的話，我們需要的是原樹上查詢點 $u$ 到其所在重鏈底端的所有矩陣的乘積，從全局平衡二叉樹的 $u$ 點開始，下面 $treefa[u]$ 表示 $u$ 在全局平衡二叉樹上的父親。

把自身節(jié)點的 $matr1$ 以及右兒子的 $matr2$ 統(tǒng)計入答案。
如果 $u$ 是父親 $treefa[u]$ 的左兒子，那么需要把父親的 $matr1$ 以及父親的右兒子的 $matr2$ 統(tǒng)計上；否則這一步不進行操作。
跳到父親。
重復執(zhí)行 2~3 步直到跳到根。

比如有一條有 $12$ 個點的重鏈，它們對應到區(qū)間上長這樣：

把他特殊建出的平衡二叉樹長這樣(圈出的點是每一層的根，只圈出了需要用到的根)：

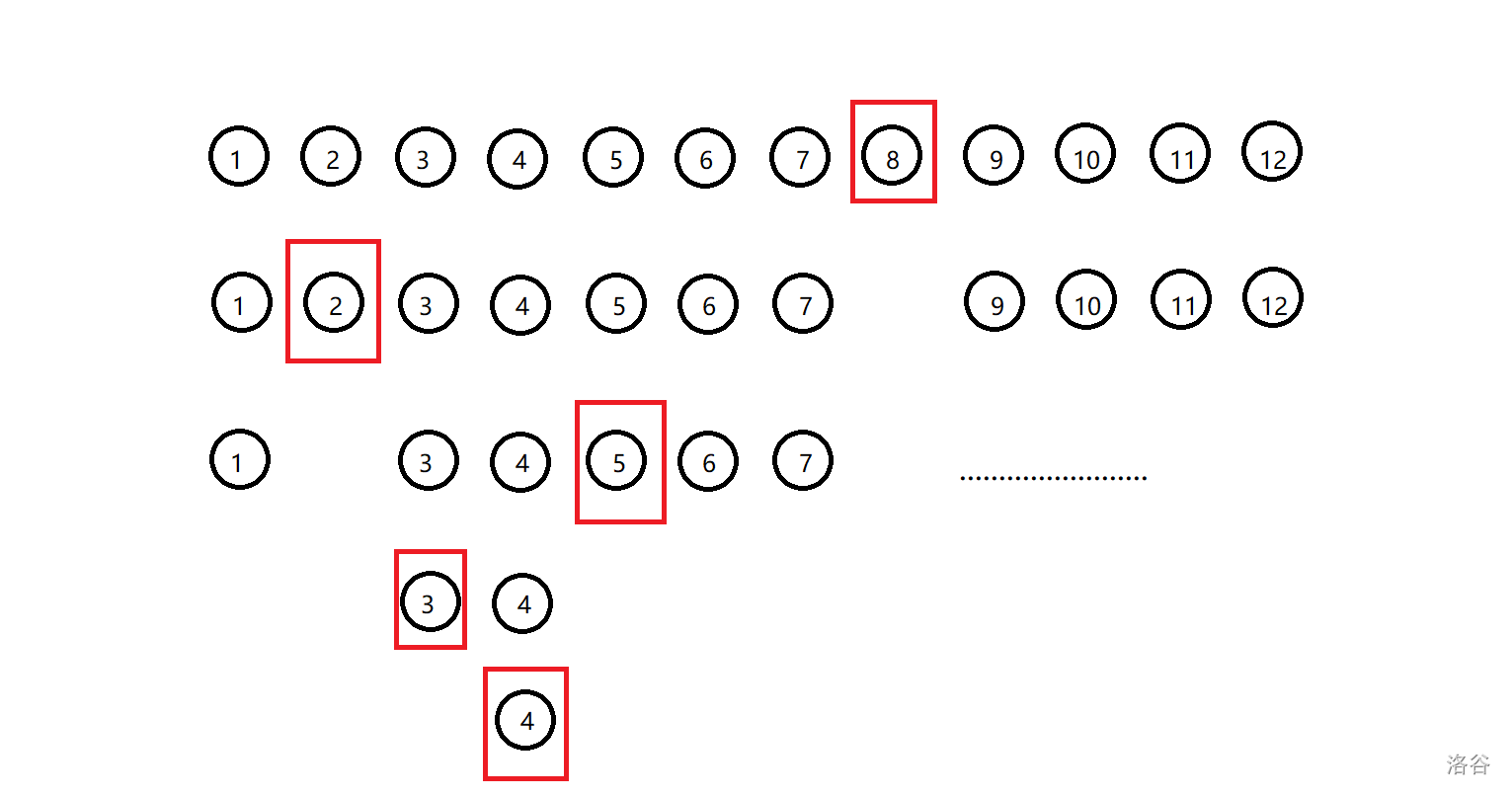
現(xiàn)在要查詢 $4$ 號點子樹內的信息，就是查詢區(qū)間 $[4,12]$ 內的點的轉移矩陣的乘積。模擬上述過程如下：

將 $4$ 號點自身的轉移矩陣和右子樹代表的區(qū)間（這個圖里沒有）的轉移矩陣的乘積計入答案。
此時計入答案的點：$4$。
因為 $4$ 號點是 $3$ 號點的右兒子所以 $3$ 號點不計入答案，然后跳到 $3$ 號點。
此時計入答案的點：$4$。
$3$ 號點是 $5$ 號點的左兒子，所以 $5$ 號點以及 $5$ 號點的右子樹代表的區(qū)間 $[6,7]$ 計入答案，并跳到 $5$ 號點。
此時計入答案的點：$4,5,6,7$。
$5$ 號點是 $2$ 號點的右兒子，不操作，并跳到 $2$ 號點。
此時計入答案的點：$4,5,6,7$。
$2$ 號點是 $8$ 號點的左兒子，將 $8$ 號點，以及右子樹區(qū)間 $[9,12]$ 計入答案。并跳到 $8$ 號點。
此時計入答案的點：$4,5,6,7,8,9,10,11,12$。
跳到根了，結束。

查詢子樹的復雜度為 $O(\log n)$。

時間復雜度分析：

如果往下的邊是輕邊，每一次子樹大小減少一半，所以至多走 $O(\log n)$ 條輕邊；
如果往下的邊是重邊，因為重邊特殊的建法，每一次取帶權中點，子樹大小也減半，所以至多走 $O(\log n)$ 條重邊。
所以樹高是 $O(\log n)$ 的。

一些細節(jié)見代碼，個人認為碼量和樹剖差不多。

code

#include<bits/stdc++.h>
#define PII pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=1e6+5,inf=0x3f3f3f3f;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,T,w[N];
int tot,head[N],to[N<<1],Next[N<<1];
void add(int u,int v){
	to[++tot]=v,Next[tot]=head[u],head[u]=tot;
}

int son[N],Size[N],lsiz[N],g[N][2],f[N][2];
void dfs1(int u,int fa){
	Size[u]=1;
	for(int i=head[u];i;i=Next[i]){
		int v=to[i];
		if(v==fa) continue;
		dfs1(v,u);
		Size[u]+=Size[v];
		if(Size[v]>Size[son[u]]) son[u]=v;
	}
	lsiz[u]=Size[u]-Size[son[u]];
}

void dfs2(int u,int fa){
	if(son[u]) dfs2(son[u],u);
	g[u][1]=w[u];
	for(int i=head[u];i;i=Next[i]){
		int v=to[i];
		if(v==fa||v==son[u]) continue;
		dfs2(v,u);
		g[u][0]+=max(f[v][0],f[v][1]);
		g[u][1]+=f[v][0];
	}
	f[u][0]=g[u][0]+max(f[son[u]][0],f[son[u]][1]);
	f[u][1]=g[u][1]+f[son[u]][0];
} 

struct Matrix{
	int n,m,a[2][2];
	void Init(){memset(a,-0x3f,sizeof a);}
}F;


Matrix operator *(Matrix A,Matrix B){
	Matrix C; C.Init();
	C.n=A.n,C.m=B.m;
	for(int i=0;i<=C.n;i++){
		for(int j=0;j<=C.m;j++){
			for(int k=0;k<=A.m;k++){
				C.a[i][j]=max(C.a[i][j],A.a[i][k]+B.a[k][j]);
			}
		}
	}
	return C;
}


struct Tree{
	int ls,rs;
	Matrix matr1,matr2;
}t[N];
void pushup(int p){
	t[p].matr2=t[p].matr1;
	//還是注意要從右往左合并，因為這個調了一個上午。 
	if(t[p].rs) t[p].matr2 =  t[ t[p].rs ].matr2 * t[p].matr2;
	if(t[p].ls) t[p].matr2 =  t[p].matr2 * t[ t[p].ls ].matr2;   //注意順序 
}
PII Getf(int p){   //得到此時 p 點的 matr2*F 的值(注意這個不一定是 p 點在原樹上的 f 值,因為 matr2 不一定是原樹上 p 到重鏈底端的所有轉移矩陣的乘積) 
	Matrix Ans=F*t[p].matr2;
	return {Ans.a[0][0],Ans.a[0][1]};
}
int treefa[N],root;
bool vis[N]; 
int st[N],top;
int SBuild(int l,int r){   //對重鏈特殊建樹 
	if(l>r) return 0; 
	int sum=0;
	for(int i=l;i<=r;i++) sum+=lsiz[st[i]];
	for(int i=l,s=lsiz[st[l]];i<=r;i++,s+=lsiz[st[i]]){
		if(s * 2 >= sum){  //帶權中點 
			int p=st[i],lson=SBuild(l,i-1),rson=SBuild(i+1,r);
			t[p].ls=lson,t[p].rs=rson;
			treefa[lson]=treefa[rson]=p;
			pushup(p);
			return p;
		} 
	}
	return 0;
}
int Build(int u){
	for(int x=u;x;x=son[x]) vis[x]=true; 
	for(int x=u;x;x=son[x]){
		for(int i=head[x];i;i=Next[i]){    //先遞歸輕兒子 
			int y=to[i];
			if(vis[y]) continue;
			treefa[Build(y)]=x;
		}
	}
	top=0;    //因為 top 是全局變量，所以不能寫在vis那里，不然在上面遞歸到 y 時就被覆蓋了！！！ 
	for(int x=u;x;x=son[x]) st[++top]=x;
	return SBuild(1,top);
}

void Init(){ //預處理除了建樹都和樹剖寫法一樣 
	dfs1(1,0); 
	dfs2(1,0);  
	
	for(int x=1;x<=n;x++){
		t[x].matr1.n=1,t[x].matr1.m=1;
		t[x].matr1.a[0][0]=g[x][0],t[x].matr1.a[0][1]=g[x][1];
		t[x].matr1.a[1][0]=g[x][0],t[x].matr1.a[1][1]=-inf;
	}
	
	F.n=0,F.m=1;
	F.a[0][0]=0,F.a[0][1]=-inf;  
	
	root=Build(1);	
	
}


void change(int u,int val){
	t[u].matr1.a[0][1]+=val-w[u];
	w[u]=val;
	for(;u;u=treefa[u]){   //這里不能寫 for(;u!=root;u=treefa[u]) 因為這樣的話根的 matr2 沒有被 pushup 更新。 
		int fa=treefa[u];
		if(fa && t[fa].ls !=u && t[fa].rs != u){  //輕邊 
			PII oldf=Getf(u);
			t[fa].matr1.a[0][0] -= max(oldf.fi , oldf.se) ;
			t[fa].matr1.a[0][1] -= oldf.fi ;
			t[fa].matr1.a[1][0] -= max(oldf.fi , oldf.se) ;
			pushup(u);
			PII newf=Getf(u);
			t[fa].matr1.a[0][0] += max(newf.fi , newf.se) ;
			t[fa].matr1.a[0][1] += newf.fi ;
			t[fa].matr1.a[1][0] += max(newf.fi , newf.se) ;			
		}
		else pushup(u);
	}
}
signed main(){
//	freopen("P4751_4.in","r",stdin);
//	freopen(".out","w",stdout);
	n=read(),T=read();
	for(int i=1;i<=n;i++) w[i]=read();
	for(int i=1;i<n;i++){
		int u=read(),v=read();
		add(u,v),add(v,u);
	}
	
	Init();
	
	int lstans=0;
	while(T--){
		int x=read()^lstans,y=read();
		change(x,y);
		PII ans=Getf(root); 
		lstans = max(ans.fi,ans.se);
		printf("%d\n",lstans);
	}
	return 0;
}

參考網(wǎng)址：動態(tài)DP之全局平衡二叉樹

54. CF1603D Artistic Partition

CF1603D Artistic Partition

題意就是讓你把序列分成 $k$ 段，使每一段的 $c$ 值的和盡可能小。

設 $f[i][k]$ 表示前 $i$ 個數(shù)，分成 $k$ 段的最小值，則：
$f[i][k] = \min_{1\le j \le i}(f[j-1][k-1]+c(j,i))$。
注意到這個狀態(tài)直接爆了，但我們會發(fā)現(xiàn)因為 $c(l,r)\ge r-l+1$,所以 $f[n][k]\ge n$。
而 $f(l,2l-1)=(2l-1)-l+1$，即 $r<2l$ 時 $f(l,r)=r-l+1$，所以如果我們分出的 $k$ 段是：
$[1,1],[2,3],[4,7],...,[2^{k-1},2^k-1]$
時，每段區(qū)間的 $c(l,r)$ 的和剛好 $=n$，即如果 $2^k-1\ge n$，答案是 $n$，所以我們需要考慮的 $k$ 就是 $\log n$ 級別的，但這樣僅僅是把狀態(tài)優(yōu)化了，時間復雜度照爆不誤。

直接暴力化簡 $c(l,r)$:

\[\begin{aligned} c(l,r) &= \sum_{i=l}^r\sum_{j=i}^r [gcd(i,j)\ge l] \\ &= \sum_{k=l}^r\sum_{i=l}^r\sum_{j=i}^r [gcd(i,j)=k] \\ &= \sum_{k=l}^r\sum_{i=\lfloor \frac{l}{k} \rfloor}^{\lfloor \frac{r}{k} \rfloor }\sum_{j=i}^{\lfloor \frac{r}{k} \rfloor } [gcd(i,j)=k] \\ &= \sum_{k=l}^r\sum_{i=\lfloor \frac{l}{k} \rfloor}^{\lfloor \frac{r}{k} \rfloor }\sum_{j=i}^{\lfloor \frac{r}{k} \rfloor } [gcd(i,j)=1] \\ &= \sum_{k=l}^r\sum_{j=\lfloor \frac{l}{k} \rfloor}^{\lfloor \frac{r}{k} \rfloor }\sum_{i=\lfloor \frac{l}{k} \rfloor}^{j} [gcd(i,j)=1]\\ &= \sum_{k=l}^r\sum_{j=1}^{\lfloor \frac{r}{k} \rfloor }\sum_{i=1}^{j} [gcd(i,j)=1]\\ &= \sum_{k=l}^r\sum_{j=1}^{\lfloor \frac{r}{k} \rfloor } \varphi(j)\\ &= \sum_{k=l}^r s(\lfloor\frac{r}{k} \rfloor)\\ \end{aligned} \]

其中 $s(i)$ 表示 1~i 的歐拉函數(shù)的和，$s$ 是可以預處理的。

盲猜一波 $c(l,r)$ 滿足四邊形不等式，那就可以決策單調性優(yōu)化了。
證明(來自題解區(qū)大佬):

設 $f(l,p,r)=\sum_{k=l}^r s(\lfloor\frac{p}{k} \rfloor)$。
對于 $l_1\le l_2\le r_1\le r_2$，我們有：

\[\begin{aligned} c(l_1,r_2)+c(l_2,r_1) &= f(l_1,r_2,r_2) + f(l_2,r_1,r_1) \\ &=(f(l_1,r_2,l_2-1) + f(l_2,r_2,r_2)) + (f(l_1,r_1,r_1) - f(l_1,r_1,l_2-1)) \\ &=f(l_1,r_2,l_2-1) - f(l_1,r_1,l_2-1) + c(l_1,r_1) + c(l_2,r_2) \\ \end{aligned} \]

那明顯這個 $f(l_1,r_2,l_2-1) - f(l_1,r_1,l_2-1) > 0$,所以 $c(l,r)$ 滿足四邊形不等式。

這里采用分治優(yōu)化復雜度，枚舉 $k$ 是 O$(\log n)$，一共 $O(\log n)$ 層，每一層轉移 $O(n)$，總時間復雜度 $O(n\log^2n)$，為了每一層的復雜度嚴格 $O(n)$,我們要支持 $O(1)$ 查詢 $c(l,r)$。
在更新 $f[mid][k]$ 時，先用數(shù)論分塊加上 $c(\min(mid,R)+1,mid)$ , 再倒敘枚舉 $j$，然后每一次加入一個 $s[mid/j]$ 即可。

如果沒有數(shù)論分塊算 $c(\min(mid,R)+1,mid)$ 的復雜度，那時間復雜度是 $O(n \log^2 n)$，加上這個就不太好算了。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=1e5+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int T,n,m; 

int pri[N],cnt;
bool stater[N];
int mn[N],mx[N],phi[N];
void Eular(){
	stater[1]=1;
	phi[1]=1;
	for(int i=2;i<N;i++){
		if(!stater[i]) pri[++cnt]=i,mn[i]=i,mx[i]=i,phi[i]=i-1;
		for(int j=1;j<=cnt&&i*pri[j]<N;j++){
			int x=i*pri[j];
			stater[x]=true;
			mn[x]=pri[j];
			if(i%pri[j]==0){
				mx[x]=mx[i]*pri[j];
				if(x!=mx[x]) phi[x]=phi[x/mx[x]]*phi[mx[x]];
				else phi[x]=x/mn[x]*(mn[x]-1);    
				break;
			}
			else{
				mx[x]=pri[j];
				phi[x]=phi[i]*phi[pri[j]];
			}
		}
	}
	for(int i=1;i<N;i++){
		phi[i]=phi[i-1]+phi[i];
	} 
}

int c(int l,int r){
	int i=l,res=0;
	while(i<=r){
		int j=r/(r/i);
		res+=(j-i+1)*phi[r/i];
		i=j+1;
	}
	return res;
}
int f[N][20];
void solve(int k,int l,int r,int L,int R){
	if(l>r) return; 
	int mid=(l+r)>>1,opt=-1,res=0;
	int C=c(min(mid,R)+1,mid);  //注意加上這個 
	for(int j=min(mid,R);j>=L;j--){
		C+=phi[mid/j];
		if(opt==-1 || f[j-1][k-1]+C<=res){
			opt=j,res=f[j-1][k-1]+C;
		}
	}
	f[mid][k]=res;
	if(l>=r) return;
	solve(k,l,mid,L,opt);
	solve(k,mid+1,r,opt,R);
}
signed main(){
	Eular();
	T=read();
		
	f[0][0]=0;
	for(int i=1;i<N;i++) f[i][0]=0x3f3f3f3f3f3f3f3f;   
	
	for(int k=1;k<=18;k++)
		solve(k,1,N-5,1,N-5);
		
	while(T--){
		n=read(),m=read();
		if(m>20||(1<<m)>n){
			printf("%lld\n",n);
			continue;
		} 
		
		printf("%lld\n",f[n][m]);
	}
	return 0;

55.CF1527E Partition Game

CF1527E Partition Game

還是先看樸素 DP:
$f[i][k]$ 表示前 $i$ 個數(shù)分為 $k$ 段的最小代價，則：$f[i][k]=\min_{0\le j < i}{f[j][k-1]+cost(j+1,i)}$

第一眼似乎這個 $cost$ 完全無法優(yōu)化求他的時間復雜度。
但是我們可以考慮 $i$ 每次移一位后 $cost$ 的變化：
對于 $cost(j,i) \to cost(j,i+1)$，

如果 $i$ 及以前最后一個 $a[i+1]$ 的位置 $lst_{a_{i+1}}\le j$，那么 $cost(j,i+1)=cost(j,i)+(i+1)-lst_{a_{i+1}}$
否則 $cost(j,i+1)=cost(j,i)$

所以這個式子：
$f[i][k]=\min_{0\le j < i}{f[j][k-1]+cost(j+1,i)}=\min_{0\le j < i}{g[j]}$
和 $i$ 變成 $i+1$ 后的：
$f[i+1][k]=\min_{0\le j < i+1}{f[j][k-1]+cost(j+1,i+1)}=\min_{0\le j < i+1}{g[j]}$。
只不過是把 $0\le j<lst_{a_{i+1}}$ 的 $g[j]$ 加上 $(i+1)-lst_{a_{i+1}}$，然后再加入一個 $g[i]$ 就可以了。

線段樹維護即可，$O(k n \log n)$。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=35000+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}

int n,k,a[N];
int lst[N],f[N][105];
struct node{
	int l,r,ming,add;
	void tag(int d){
		ming+=d;
		add+=d;
	}
};
struct SegmentTree{
	node t[N<<2];
	void pushup(int p){
		t[p].ming=min(t[p<<1].ming,t[p<<1|1].ming); 
	}
	void spread(int p){
		if(t[p].add){
			t[p<<1].tag(t[p].add);
			t[p<<1|1].tag(t[p].add);
			t[p].add=0;
		}
	}
	void build(int p,int l,int r){
		t[p].l=l,t[p].r=r,t[p].add=0;    //add也要清空 
		if(l==r){
			t[p].ming=0;
			return;
		}	
		int mid=(l+r)>>1;
		build(p<<1,l,mid);
		build(p<<1|1,mid+1,r);
		pushup(p);
	} 
	void change(int p,int l,int r,int d){
		if(l<=t[p].l&&t[p].r<=r){
			t[p].tag(d);
			return;
		}
		spread(p);
		int mid=(t[p].l+t[p].r)>>1;
		if(l<=mid) change(p<<1,l,r,d);
		if(r>mid) change(p<<1|1,l,r,d);
		pushup(p);
	}
	int ask(int p,int l,int r){
		if(l<=t[p].l&&t[p].r<=r){
			return t[p].ming;
		}	
		int mid=(t[p].l+t[p].r)>>1,res=LLONG_MAX;
		if(l<=mid) res=min(res,ask(p<<1,l,r));
		if(r>mid) res=min(res,ask(p<<1|1,l,r));
		return res;
	}
}Seg;
signed main(){
	n=read(),k=read();
	for(int i=1;i<=n;i++) a[i]=read();	
	
	memset(f,0x3f,sizeof f);
	f[0][0]=0;
	for(int j=1;j<=k;j++){
		Seg.build(1,0,n-1); 
		for(int i=1;i<=n;i++) lst[i]=0;
		for(int i=1;i<=n;i++){
			if(lst[a[i]]){
				Seg.change(1,0,lst[a[i]]-1,i-lst[a[i]]);
			}
			Seg.change(1,i-1,i-1,f[i-1][j-1]);   //cost(i,i)就省略了 
			lst[a[i]]=i;
			f[i][j]=Seg.ask(1,0,i-1);
		}
	}
	printf("%lld\n",f[n][k]);
	return 0;
}

56.CF1476F Lanterns

CF1476F Lanterns

比較考驗思維，直接講做法了。

$f[i]$ 表示前 $i$ 盞燈可以覆蓋的最長前綴,轉移:

$f[i-1]<i$，那可能 $i$ 照的那一段就接不上 $f[i-1]$ 了，$f[i]=f[i-1]$。
$f[i-1]\ge i$，那么 $i$ 肯定往右照，$f[i]=\max(f[i-1],i+p_i)$。
存在一個 $t$ ($0\le t<i$) ,雖然 $f[t]<i$，但是 $i$ 往左照后可以與它接起來，即滿足 $f[t]\ge i-p_i-1$，此時原先那些 $t<j<i$，原先有可能無法被覆蓋，現(xiàn)在他們肯定統(tǒng)一往右照最優(yōu)，$f[i]=\max(i-1 , \max_{t<j<i} (j+p_j))$。（注意 $i$ 自己照不到自己）。
因為有第一個轉移，所以 $f$ 肯定有單調性，二分出最靠左的 $t$ (這樣一定最優(yōu))，進行轉移 $3$。后面的轉移區(qū)間 RMQ 即可。

code

#include<bits/stdc++.h>
#define PII pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=3e5+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int T,n,p[N],st[N][30]; 
int f[N];
PII from[N];   //第二維是1代表朝右，0代表超左 
int RMQ(int l,int r){
	if(l>r) return 0;
	int k=log(r-l+1)/log(2);
	return max(st[l][k],st[r-(1<<k)+1][k]);
}
void print(int u){
	if(u==0||u==-1) return;
	if(from[u].se){
		print(from[u].fi);
		putchar('R');
	}
	else{
		print(from[u].fi);
		for(int i=from[u].fi+1;i<=u-1;i++) putchar('R');
		putchar('L');
	}
}
signed main(){
	T=read();
	while(T--){
		n=read();
		for(int i=1;i<=n;i++) p[i]=read(),st[i][0]=i+p[i];
		for(int t=1;t<=20;t++){
			for(int i=1;i+(1<<t)-1<=n;i++){
				st[i][t]=max(st[i][t-1],st[i+(1<<(t-1))][t-1]);
			}
		}

		for(int i=1;i<=n;i++){
			if(f[i-1]<i) f[i]=f[i-1],from[i]={-1,-1};
			else f[i]=max(f[i-1],i+p[i]),from[i]={i-1,1};   
			int l=0,r=i-1,mid,t=-1;
			while(l<=r){
				int mid=(l+r)>>1;
				if(f[mid]>=i-p[i]-1) t=mid,r=mid-1;
				else l=mid+1;
			}	
			if(t!=-1){
				if(max(i-1,RMQ(t+1,i-1))>f[i]){
					f[i]=max(i-1,RMQ(t+1,i-1));
					from[i]={t,0};
				}
			}
		}
		
		if(f[n]<n) puts("NO");
		else puts("YES"),print(n),puts("");
	}
	return 0;
}

57.劃分（part）

劃分（part）

因為是內部題，所以這個鏈接可能會掛，所以講一下題意：

題意簡述

對于一個正整數(shù)序列 $a_i$，若它可以被劃分為兩個不相交的子序列（可以不連續(xù)，每個位置恰好屬于其中
一個子序列），兩個子序列的和相等，那么稱這個序列為好序列。
對于一個正整數(shù)序列，若其所有長度為 $k$ 的連續(xù)子序列都是好序列，那么稱這個序列為 $k-序列\(zhòng))。
給你個正整數(shù)序列，對于每個序列，求出它是 \(k-序列\(zhòng)) 的所有 \(k$ 的值。

數(shù)據(jù)范圍：$1\le n \le 10^3$，$1\le \sum A_i \le 10^5$。

題解

對于每個 $k$，倒序枚舉左端點，左端點往左移的時候用，$f[s]$ 表示選出若干個和為 $s$ 的數(shù)，右端點最靠左是多少(靠右顯然不優(yōu))，維護出 $f$ 后再對每個 $r$ 看一下是否有 $sum \equiv 0\pmod 2 \land f[\frac{sum}{2}]<=r$，其中 $sum=\sum_{i=l}^r a_i$。

轉移用背包即可，$O(T n V)$。

code

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+5,M=1e5+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int T,n,a[N],pre[N];
bool flag[N];
int f[M];
vector<int> ans;
signed main(){
	freopen("part.in","r",stdin);
	freopen("part.out","w",stdout);
	T=read();
	while(T--){
		n=read();
		for(int i=1;i<=n;i++) a[i]=read(),pre[i]=pre[i-1]+a[i],flag[i]=true;
		memset(f,0x3f,sizeof f);
		for(int l=n;l>=1;l--){
			for(int s=pre[n]/2;s>=a[l];s--) f[s]=min(f[s],f[s-a[l]]);
			f[a[l]]=l;
			for(int r=l;r<=n;r++){
				int sum=pre[r]-pre[l-1];
				if(sum%2==1) flag[r-l+1]=false;
				else if(f[sum/2]>r) flag[r-l+1]=false;
			}
		}
		ans.clear();
		for(int i=1;i<=n;i++)
			if(flag[i]) ans.push_back(i);
		printf("%d ",ans.size());
		for(int i=0;i<ans.size();i++){
			if(i==ans.size()-1) printf("%d",ans[i]);
			else printf("%d ",ans[i]);
		}
		puts("");
	}
	return 0;
}

58.超級馬里奧（mario）

超級馬里奧（mario）

也是內部題，但是題面很長，直接貼圖：

以下 $c_i$ 統(tǒng)一已經(jīng)對 $C$ 取 $\min$。

注意到一個點上如果選擇吃東西，那能量是直接賦值而不是累加。
所以如果枚舉了哪些點要吃東西，那么任意相鄰的兩點之間就不能再補充能量了，能用的能量只跟上一個點的 $c_i$ 有關。

設 $d[i][j]$ 表示在 $i$ 吃東西，走不超過 $c_i$ 條邊到 $j$,最多能走的路程 (中間不再吃東西)。
我們先不考慮這東西怎么求，假設我們已經(jīng)預處理出來了。

設 $dp[sum][i]$ 表示起點在 $i$ 號節(jié)點，有 $sum$ 元錢，恰好用完，最多能走多少。
首先 $i$ 號點是一定要吃東西的，不然沒能量，考慮枚舉下一個吃東西的點 $j$，則 $d[i][j]+dp[sum-p[i]][j] \to dp[sum][i]$，因為 $q_i<=n^2$ 所以這個 dp 的復雜度是 $O(n^4)$。
回答詢問時，先對它進行一次前綴 $\max$ (就得到 "花不超過 $sum$ 元錢能走的最長路線" )，然后二分求出需要花的最少錢數(shù)即可。

現(xiàn)在看 $d[i][j]$ 的求法,考慮倍增優(yōu)化 dp。
設 $f[k][i][j]$ 表示從 $i$ 開始，走不超過 $2^k$ 條邊，到 $j$ 的最長路徑。
轉移時枚舉中轉點 $u$，則 $f[k-1][i][u]+f[k-1][u][j] \to f[k][i][j]$。
這個 dp 的復雜度是 $O(n^3 \log c_i)$。

有了 $f$ 來看怎么求 $d$：
考慮對 $c_i$ 做一個二進制拆分，設 $c_i=2^{a_1}+2^{a_2}+...2^{a_k} (a_1>a_2>...>a_k)$。
一開始 $d[i][j]$ 僅僅表示從 $i$ 開始，走不超過 $0$ 條邊，到 $j$ 的最長路徑，即除了 $f[i][i]=0$，其余都是 $-\infty$。
我們現(xiàn)在要將它擴展到:從 $i$ 開始，走不超過 $2^{a_1}$ 條邊，到 $j$ 的最長路徑：
那么枚舉中轉點 $u$，所以有轉移 $d[i][u]+f[a1][u][j] \to d[i][j]$ , 為了防止用來轉移的 $d$ 數(shù)組已經(jīng)被更新過了，可以先用輔助數(shù)組存一下。
這個過程非常像矩陣乘法，當然這里可以不寫矩乘。如此不斷擴展即可直到 $d[i][j]$ 表示走不超過 $2^{a_1}+2^{a_2}+...2^{a_k}$ 條邊，到 $j$ 的最長路徑為止。
這個 dp 的復雜度是:

枚舉 $i$，$O(n)$；
對每一個二進制位做一次擴展，$O(\log c_i)$；
枚舉 $j$，$O(n)$；
枚舉 u，$O(n)$。

則這個 dp 的復雜度是 $O(n^3 \log c_i)$。

于是就寫完了，圖都不用建，注意重邊只需要取最長的那一條。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=1e2+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,m,C,T;
int p[N],c[N],dist[N][N];  //dist:鄰接矩陣 

int f[20][N][N];
void DP_f(){
	memset(f,-0x3f,sizeof f);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(i==j) f[0][i][j]=0;
			else if(dist[i][j]) f[0][i][j]=dist[i][j];
	
	for(int k=1;k<=18;k++)
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++)
				for(int u=1;u<=n;u++)
					f[k][i][j]=max(f[k][i][j],f[k-1][i][u]+f[k-1][u][j]);
}

int d[N][N],tmp[N];
void DP_d(){
	memset(d,-0x3f,sizeof d);
	for(int i=1;i<=n;i++){
		vector<int> a;
		for(int j=18;j>=0;j--) if(c[i]>>j&1) a.push_back(j);
		d[i][i]=0;
		for(int k:a){
			memset(tmp,-0x3f,sizeof tmp);
			for(int j=1;j<=n;j++){
				for(int u=1;u<=n;u++){
					tmp[j]=max(tmp[j],d[i][u]+f[k][u][j]);
				}
			}
			for(int j=1;j<=n;j++) d[i][j]=tmp[j];
		}
	}
}

int dp[N*N][N];
void DP_dp(){
	memset(dp,-0x3f,sizeof dp);
	for(int i=1;i<=n;i++) dp[0][i]=0;
	for(int sum=1;sum<=n*n;sum++){
		for(int i=1;i<=n;i++){
			if(p[i]>sum) continue;
			for(int j=1;j<=n;j++){
				dp[sum][i]=max(dp[sum][i],d[i][j]+dp[sum-p[i]][j]);
			}
		}
	} 
} 
signed main(){
	freopen("mario.in","r",stdin);
	freopen("mario.out","w",stdout);
	n=read(),m=read(),C=read(),T=read();
	for(int i=1;i<=n;i++){
		p[i]=read(),c[i]=read();
		c[i]=min(c[i],C);
	}
	for(int i=1;i<=m;i++){
		int u=read(),v=read(),l=read();
		dist[u][v]=max(dist[u][v],l);
	}
	
	DP_f();
	DP_d();
	DP_dp();
	
	for(int i=1;i<=n;i++)
		for(int sum=1;sum<=n*n;sum++)
			dp[sum][i]=max(dp[sum-1][i],dp[sum][i]);

	while(T--){
		int s=read(),q=read(),d=read();
		int l=0,r=q,mid,ans=-1;
		while(l<=r){
			mid=(l+r)>>1;
			if(dp[mid][s]>=d) ans=mid,r=mid-1;
			else l=mid+1;
		}
		if(ans==-1) puts("-1");
		else printf("%lld\n",q-ans);
	} 
	return 0;
}

59.CF685E Travelling Through the Snow Queen's Kingdom

CF685E Travelling Through the Snow Queen's Kingdom

這個故事告訴我們考場想出狀態(tài)后不管會不會爆都要嘗試一下...

設 $f[i][x][y]$ 表示從第 $i$ 天開始，要從 $x$ 到 $y$，到達時的最小日期，不行則 $=m+1$。
一開始 $f[m+1][x][y]=m+1,f[i][x][x]=i$。
當 $i$ 從 $i$ 變成 $i-1$ 時，假設第 $i$ 條邊是 $(u,v)$。

如果 $x\neq u$ 且 $x\neq v$ 那么這條邊不會帶來任何影響，因為 $x$ 根本無法在 $i$ 天之前走到 $u/v$，$f[i-1][x][y]=f[i][x][y]$。
當 $x=u$ 時，我可以選擇走這條邊，走過去之后時間變成 $i$,那么 $f[i-1][u][y]=\min(f[i][u][y],f[i][v][y]$。
當 $x=v$ 時同理。

倒敘處理天數(shù)并回答詢問即可，時間復雜度 $O(nm)$。

考場我以為這個dp時間復雜度不對就沒寫...

code

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+5,M=2e5+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,m,u[M],v[M],q;
int f[N][N];
struct P{
	int l,r,s,t,id;
};
vector<P> que[M];
bool ans[M];
signed main(){
	freopen("plan.in","r",stdin);
	freopen("plan.out","w",stdout);
	n=read(),m=read(),q=read();
	for(int i=1;i<=m;i++){
		u[i]=read(),v[i]=read();
	}
	for(int i=1;i<=q;i++){
		int l=read(),r=read(),s=read(),t=read();
		que[l].push_back({l,r,s,t,i});
	}
	for(int x=1;x<=n;x++){
		for(int y=1;y<=n;y++){
			f[x][y]=m+1;
		}
	}
	for(int i=m+1;i>=1;i--){
		for(int x=1;x<=n;x++) f[x][x]=i;
		for(int y=1;y<=n;y++)
			f[u[i]][y]=min(f[u[i]][y],f[v[i]][y]);
		for(int y=1;y<=n;y++)
			f[v[i]][y]=min(f[v[i]][y],f[u[i]][y]);
		for(P pro:que[i]){
			ans[pro.id]=(f[pro.s][pro.t]<=pro.r);
		}
	}
	
	for(int i=1;i<=q;i++)	
		if(ans[i]) puts("Yes");
		else puts("No");
	return 0;
}

60.CF1039D You Are Given a Tree

CF1039D You Are Given a Tree

先考慮樹形DP怎么求一個 $k$ 的答案:
$f[u]$ 表示 $u$ 這棵子樹內的答案，$g[u]$ 表示如果 $u$ 不在 $f[u]$ 中的鏈里，$u$ 往下的最長鏈是什么。
設 $mx_1,mx_2$ 表示 $u$ 的兒子 $v$ 中 $g[v]$ 的最大和次大值，那么先令 $f[u]=\sum f[v]$，然后：

如果 $mx_1+mx_2+1\ge k$：$f[u]=f[u]+1，g[u]=0$。
$g[u]=mx_1+1$;

容易發(fā)現(xiàn)答案單調不增，并且對于 $\sqrt n \le k \le n$，有 $1\le ans\le \sqrt n$。

這啟示我們根號分治，假設我們 $1\le k<B$ 的 $k$ 暴力樹形DP，$B\le k\le n$ 的 $k$ 我們考慮二分:
枚舉 $ans$，二分出答案是 $ans$ 的 $k$ 的區(qū)間，我們只需要知道右端點就ok了。
二分的 check 就是跑一遍樹形DP。

時間復雜度是:$O(Bn+\frac{n^2}{B}\log n)$，$B$ 應該取 $\sqrt{n\log n}$ 。

然后如果你的根號分治 TLE 了，這里有個經(jīng)典卡常技巧：把樹搞成dfs序，然后倒著掃，就可以避免每一次dfs遞歸了。

code

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,m;
int tot,head[N],to[N<<1],Next[N<<1];
void add(int u,int v){
	to[++tot]=v,Next[tot]=head[u],head[u]=tot;
}

int fa[N],rev[N],num;
void DFS(int u,int Fa){
	fa[u]=Fa;
	rev[++num]=u;   //把樹拍成dfs序 
	for(int i=head[u];i;i=Next[i]){
		int v=to[i];
		if(v==Fa) continue;
		DFS(v,u);
	}
}
int f[N],g[N],mx1[N],mx2[N];
void dfs(int k){
	for(int i=1;i<=n;i++) f[i]=g[i]=mx1[i]=mx2[i]=0;
	for(int i=num;i>=1;i--){
		int u=rev[i];
		if(1+mx1[u]+mx2[u]>=k) f[u]++;
		else g[u]=mx1[u]+1;
		if(!fa[u]) continue;
		f[fa[u]]+=f[u];
		if(g[u]>mx1[fa[u]]) mx2[fa[u]]=mx1[fa[u]],mx1[fa[u]]=g[u];
		else mx2[fa[u]]=max(mx2[fa[u]],g[u]);
	}
}
bool check(int k,int ans){
	dfs(k);
	return f[1]>=ans;
}
signed main(){
	n=read();
	for(int i=1;i<n;i++){
		int u=read(),v=read();
		add(u,v),add(v,u);
	}

	DFS(1,0);
	m=sqrt(n*log2(n));
	for(int k=1;k<=m;k++){
		dfs(k);
		printf("%d\n",f[1]);
	}
	
	int lst=m+1;
	for(int ans=n/m+1;ans>=0;ans--){
		int l=lst,r=n,mid,res=-1;
		while(l<=r){
			mid=(l+r)>>1;
			if(check(mid,ans)) l=mid+1,res=mid;
			else r=mid-1;
		}
		if(res==-1) continue;
		for(int k=lst;k<=res;k++) printf("%d\n",ans);
		lst=res+1;
	}
	return 0;
}

posted @ 2024-11-15 18:46 Green&White 閱讀(87) 評論(0) 收藏舉報

刷新頁面返回頂部

OIer_Cyq

動態(tài)規(guī)劃題單2

31.CF1580D Subsequence

code

32.P1220 關路燈

code

33.搶鮮草

code

34.P4161 [SCOI2009] 游戲

code

35.P6280 [USACO20OPEN] Exercise G

code

36.P6570 [NOI Online #3 提高組] 優(yōu)秀子序列

code

37.CF1280D Miss Punyverse

code

38.CF1500D Tiles for Bathroom

code

39.CF1276D Tree Elimination

code

40.P1081 [NOIP2012 提高組] 開車旅行

code

41.P9197 [JOI Open 2016] 摩天大樓 / Skyscraper

code

42.Count The Repetitions*

code

43.CF1788E Sum Over Zero

code

44.CF1799D2 Hot Start Up (hard version)

code

45.CF1304F2 Animal Observation (hard version)

code

46.夏蟲（summer）

題意簡述:

題解:

code

47.任務安排

code

48.任務安排2

code

49.[SDOI2012] 任務安排

code

50.忘情

code

51.CF229D Towers

code

52.【模板】"動態(tài) DP"&動態(tài)樹分治

code

53.【模板】"動態(tài)DP"&動態(tài)樹分治（加強版）

code

54. CF1603D Artistic Partition

code

55.CF1527E Partition Game

code

56.CF1476F Lanterns

code

57.劃分（part）

題意簡述

題解

code

58.超級馬里奧（mario）

code

59.CF685E Travelling Through the Snow Queen's Kingdom

code

60.CF1039D You Are Given a Tree

code

公告