• Update on 2025.5.9：修改了例題——忘情中的一些致命錯(cuò)誤，并改了一些 Latex。
• Update on 2025.9.16：此文 bug 有點(diǎn)多，已經(jīng)發(fā)布了重構(gòu)版：DP 凸性優(yōu)化：wqs 二分，建議去那邊看。

在看 wqs 二分前建議先去看另一篇博客——斜率優(yōu)化，對(duì)凸包等知識(shí)點(diǎn)有所了解。

介紹

wqs 二分最初由王欽石在他的 2012 年國(guó)家集訓(xùn)隊(duì)論文中提出，也叫"帶權(quán)二分"，或者"dp凸優(yōu)化"，而從 IOI 2016 的 Aliens 題目開(kāi)始，這種方法開(kāi)始逐步在競(jìng)賽圈中有了一定的地位。在國(guó)內(nèi)我們一般稱(chēng)為「wqs 二分」，而在國(guó)外一般稱(chēng)為「Alien Trick」。

適用題型

wqs 二分的題目一般有以下特點(diǎn):

• 題目?jī)?nèi)容形式為:有 \(n\) 個(gè)物品，從中選出 \(m\) 個(gè)，要求最后的權(quán)值最小/最大。
• 直接 dp 設(shè) \(f_{i,j}\) 表示前 \(i\) 個(gè)選出 \(j\) 個(gè)物品的話，轉(zhuǎn)移是 \(f_{i,j}=\min_k(f_{k,j-1} + Val(k,i))\),其中\(Val(k,i)\) 表示這次轉(zhuǎn)移帶來(lái)的權(quán)值。時(shí)間復(fù)雜度無(wú)論如何都是 \(O(n^2)\) 及以上的。
• 如果沒(méi)有選 \(m\) 這個(gè)限制，那可以優(yōu)化到更低復(fù)雜度,并且可以算出此時(shí)最優(yōu)方案選的數(shù)的個(gè)數(shù)。
• 選的個(gè)數(shù)越多，最終權(quán)值越小/越大，即如果設(shè) \(g(x)\),表示選 \(x\) 可以得到的最小/最大權(quán)值，那么 \(g(x)\) 的圖像構(gòu)成一個(gè)凸包。

當(dāng)然 wqs 二分不止應(yīng)用于 DP 題，具體看例題。

解法

假設(shè) \(g(x)\) 的圖像為上凸包，要求的是最大值，不妨畫(huà)一下 \(g(x)\) 的大致圖像(當(dāng)然其實(shí)我們是一個(gè)點(diǎn)都求不出來(lái)的)：

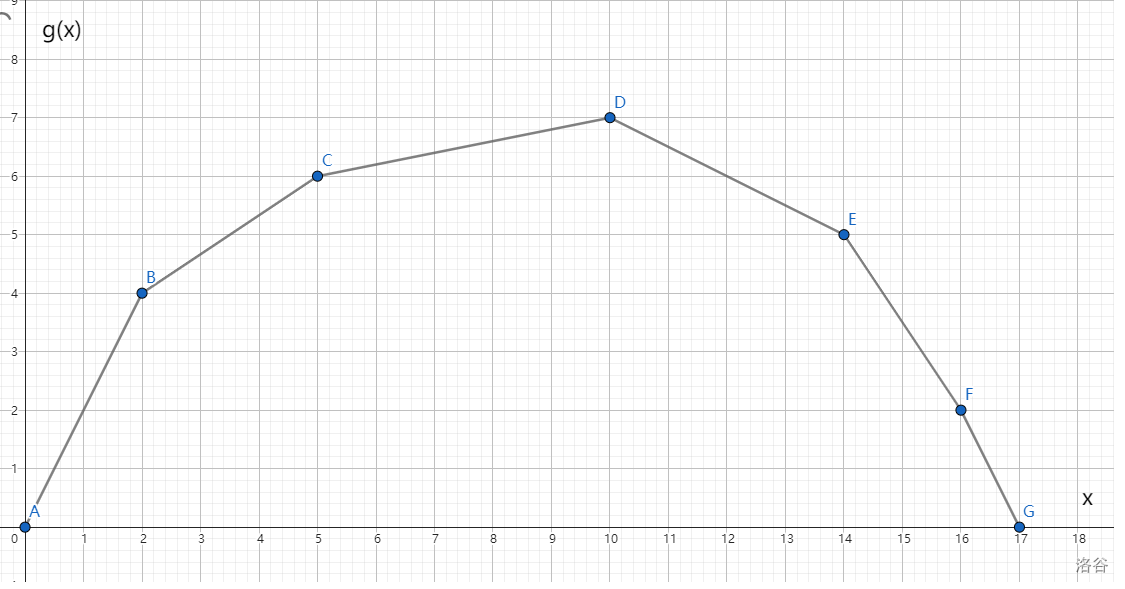
假設(shè)我們現(xiàn)在用一條直線 \(y=Kx+b\) 去切一個(gè)點(diǎn) \((x,g(x))\)，那么可以得到 \(g(x)=Kx+b\)，即這個(gè)點(diǎn)的坐標(biāo)也可以表示成 \((x,Kx+b)\)。
又因?yàn)樯贤拱袀€(gè)性質(zhì)，一條斜率為 \(K\) 的直線在他與這個(gè)凸包的切點(diǎn)處截距最大，也就是說(shuō)如果我們能求出這個(gè)最大截距，并知道此時(shí)的橫坐標(biāo)，就能知道那個(gè)切點(diǎn)的具體坐標(biāo)了。
因?yàn)橥拱男甭适菃握{(diào)的，所以隨著 \(K\) 的減小，切到的 \(x\) 也越大，所以可以二分這個(gè) \(K\),我們可以根據(jù)切點(diǎn)的坐標(biāo)去調(diào)整 \(K\) 直到切到 \((m,g(m))\) 為止，。

現(xiàn)在的問(wèn)題就是怎么求最大截距，因?yàn)槲覀儔焊恢肋@個(gè)凸包長(zhǎng)什么樣子。
會(huì)發(fā)現(xiàn) \(b = g(x)-Kx\),定義 \(h(x) = g(x)-Kx\)，如果我們能以較低的復(fù)雜度求出最大的 \(h(x)\) 以及此時(shí)的 \(x\),也就求出了我們要的東西。
考慮給 \(h(x)\) 定義一個(gè)合理的意義，不難發(fā)現(xiàn)他其實(shí)就是給每個(gè)物品多加了一個(gè) \(-K\) 的權(quán)值(所以叫代權(quán)二分)，選了這個(gè)數(shù)就要 \(-K\)。
而我們要求 \(h(x)\) 的最大值是沒(méi)有限制要選多少個(gè)的，所以 dp 時(shí)直接 \(f_i = \max_j(f_j + Val(j,i) - K)\) 即可，比一開(kāi)始那個(gè)少了一維，會(huì)更好求,具體的優(yōu)化方法/求法因題目而異，在例題中會(huì)講。
注意最后的求 \(g(x)\) 時(shí)，要記得把 \(Kx\) 加上。

關(guān)于wqs二分的實(shí)現(xiàn)細(xì)節(jié)也在例題中。

例題

忘情

把式子變成 $((\sum_{i=1}^n x_i)+1)^2 $，設(shè) \(S\) 為前綴和，那么樸素的 dp 是:
設(shè) \(f_{i,j}\) 表示前 \(i\) 個(gè)數(shù)劃分成 \(j\) 段的最小值，轉(zhuǎn)移為 \(f_{i,j}=\min_{0\le k<i}(f_{k,j-1} + (S_i - S_k + 1)^2)\)。
容易證明 \((a+b+1)^2 > (a+1)^2 + (b+1)^2\)，也就是說(shuō)分的段數(shù)越多答案越小，即按照上面的定義 \(g(x)\) 表示分 \(x\) 段的最小值，那么 \(g(x)\) 的圖像應(yīng)該是一個(gè)下凸殼:

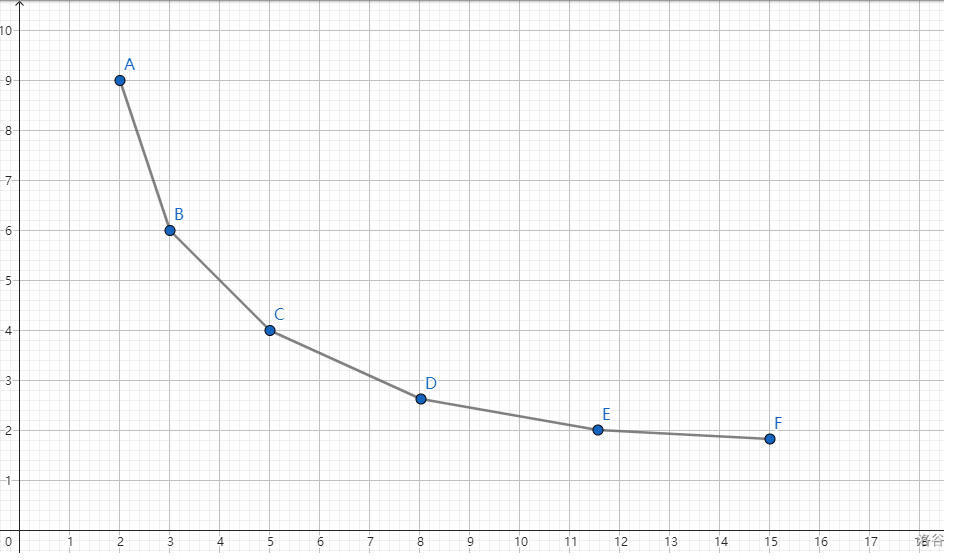
二分一個(gè)斜率 \(K\)，用斜率 \(K\) 的直線去切這個(gè)凸包，那么截距 \(b=h(x)=g(x)-Kx\),因?yàn)槭窍峦拱晕覀円笞钚〗鼐啵窗岩欢蔚臋?quán)值定義成 \(((\sum x_i)+1)^2 - K\),然后去掉段數(shù)限制，求最小答案。
考慮對(duì)這個(gè)新的問(wèn)題 dp，設(shè) \(dp_i\) 表示前 \(i\) 個(gè)數(shù)的最小值，\(dp_i=\min_{0\le j<i}(dp_j + (S_i-S_j+1)^2 - K)\),因?yàn)檫€要求此時(shí)的橫坐標(biāo) \(x\)，所以還要額外記一個(gè) dp 數(shù)組，轉(zhuǎn)移也是顯然的。
這是經(jīng)典的斜率優(yōu)化形式，可以用單調(diào)隊(duì)列優(yōu)化到 \(O(n)\),不會(huì)斜率優(yōu)化的戳這里。
總時(shí)間復(fù)雜度 \(O(n \log n)\)。

wqs 二分一些實(shí)現(xiàn)的細(xì)節(jié)：

1. 這里因?yàn)槭窍峦拱孕甭?\(K\) 是負(fù)的，但是為了方便二分時(shí)我們把他變成正的，所以 check 里 dp 變成 \(dp_i=\min_{0\le j<i}(dp_j + (S_i-S_j+1)^2 + K)\) , 原來(lái)二分要把斜率調(diào)大的就調(diào)小。
2. 注意凸包可能會(huì)有一些斜率相同的線段，即可能用一條斜率為 \(mid\) 的直線去切會(huì)切到很多個(gè)點(diǎn)，但顯然我們只能求出來(lái)一個(gè)點(diǎn)，此時(shí)我們需要保證我們求出來(lái)的點(diǎn)是橫坐標(biāo)最大的或者最小的，否則很可能會(huì)漏掉正解的位置。在本題中如果我們?cè)?\(check\) 里的斜率優(yōu)化 dp，在 \(h\) 值相同時(shí)取的是靠左的點(diǎn)，那么二分寫(xiě)的就是: 如果返回的那個(gè) \(x\le m\)，那就更新答案并把斜率調(diào)大(這里還認(rèn)為斜率是負(fù)的，不進(jìn)行 1. 的轉(zhuǎn)換) ; 相反，如果我們?cè)?\(check\) 里的斜率優(yōu)化 dp，在 \(h\) 值相同時(shí)取的是靠右的點(diǎn)，那么二分寫(xiě)的就是: 如果返回的那個(gè) \(x \ge m\),那就更新答案并把斜率調(diào)小。看取的是靠左還是靠右只要看斜率優(yōu)化維護(hù)凸包時(shí)寫(xiě)的是 >= 還是 >,> 就是取靠左的，>= 就是取靠右的。

code

變量名稍有不同。

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=1e5+5,inf=1e18;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}

int n,m,a[N]; 
int dp[N],g[N];  //dp[i]表示前 i 個(gè)數(shù)分成若干段的最小值，g[i] 表示取到最小值分的段樹(shù) 
int dq[N],l,r;
int calc(int j){  //求縱坐標(biāo) 
	return dp[j]+a[j]*a[j]-2ll*a[j];
} 
void check(int mid){
	l=1,r=0;
	dp[0]=0,g[0]=0;   
	dq[++r]=0;  //放 0 不是 1，因?yàn)榭梢宰猿?1 段。 
	for(int i=1;i<=n;i++){
		while(l<r && ( calc(dq[l+1]) - calc(dq[l]) ) < (2ll * a[i] * (a[dq[l+1]] - a[dq[l]]))) l++;  //把開(kāi)頭斜率小于當(dāng)前斜率的線段 pop 掉
		int j=dq[l];
		dp[i]=dp[j]+(a[i]-a[j]+1ll)*(a[i]-a[j]+1ll)+mid;
		g[i]=g[j]+1ll;
		while(l<r && ( calc(i) - calc(dq[r]) ) * ( a[dq[r]] - a[dq[r-1]]) < ( calc(dq[r]) - calc(dq[r-1] ) ) * ( a[i] - a[dq[r]] )) r--;  //維護(hù)凸殼
		dq[++r]=i; 
	}
}
signed main(){
	n=read(),m=read();
	for(int i=1;i<=n;i++) a[i]=read(),a[i]+=a[i-1];
	int l=0,r=inf,mid,ans=0;   //實(shí)際上斜率是負(fù)的，但是移項(xiàng)之后:b=f(x)-kx,所以就干脆把 k 取成正的，這樣在check里是每一段+mid,而不是-mid 
	while(l<=r){
		mid=(l+r)>>1;
		check(mid);
		if(g[n]<=m) r=mid-1,ans=mid;
		else l=mid+1; 
	}
	check(ans);
	printf("%lld\n",dp[n]-ans*m);  //這里要減掉 mid(也就是最后的 ans) 帶來(lái)的貢獻(xiàn) 
	return 0;
}