前置數學知識

1.一次函數

初中數學知識，見八年級數學課本。

2.凸包(凸殼)

• 定義：
  意思是點集的邊界,是一組連接相鄰兩點的線段斜率單調的一組點集，其中斜率單調遞增的叫下凸殼,單調遞減的叫上凸殼(摘自《算法競賽進階指南》)。
  注意:對于正的斜率是越陡越大，對于負的斜率是越平越大
  下面的是兩個上凸殼：
  
  
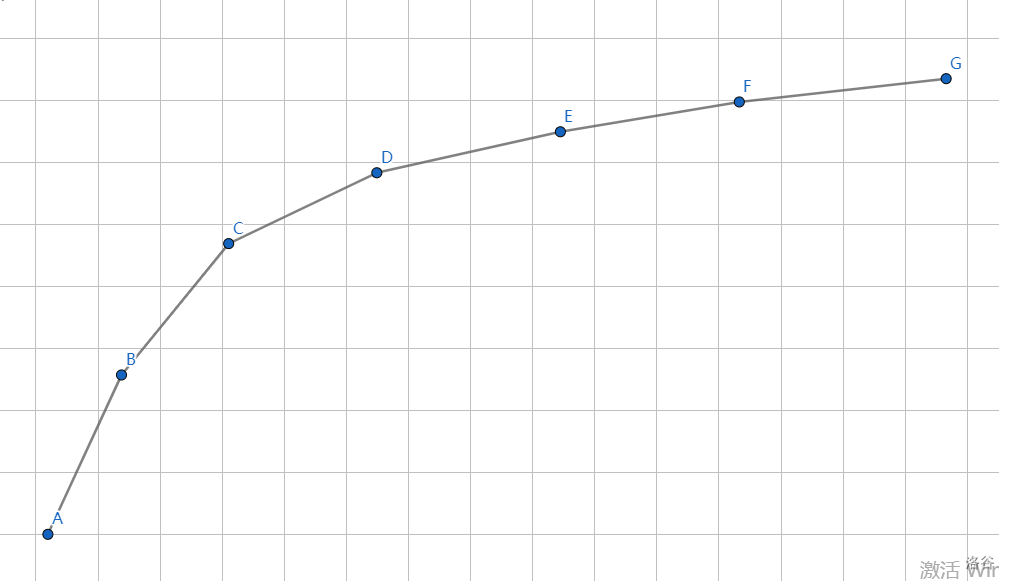
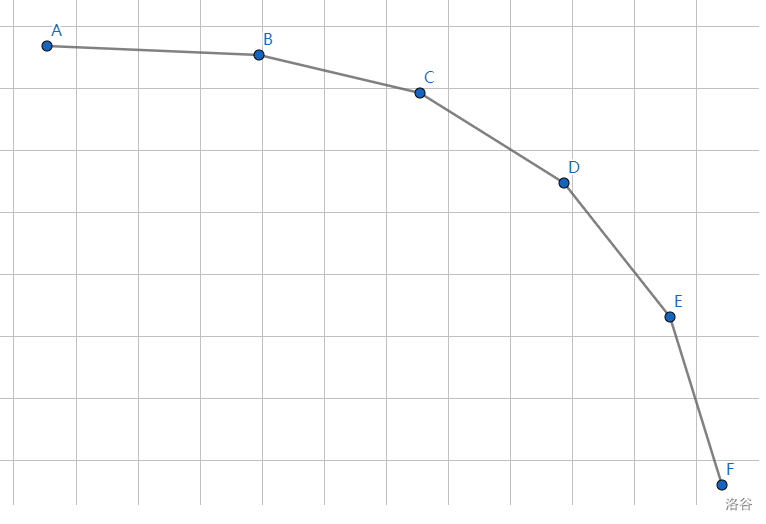
  同理，下面是兩個下凸殼:
  
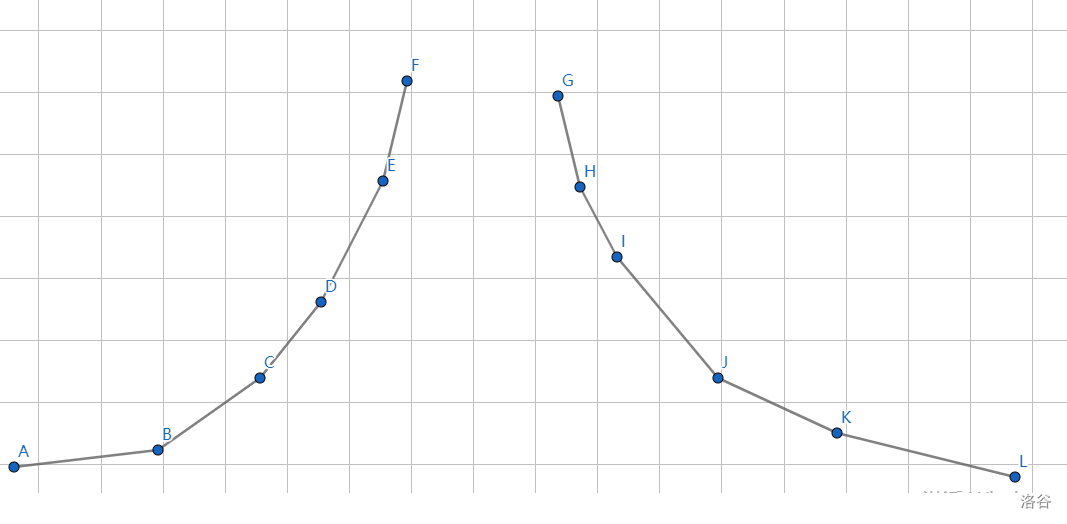
  其實上凸殼還是下凸殼直接看形狀就可以了。
• 性質：
  我們以上凸殼為例，嘗試用一條斜率固定為 \(k\) 的直線去切凸殼點集中的那些點，會得到這么多條平行線:
  
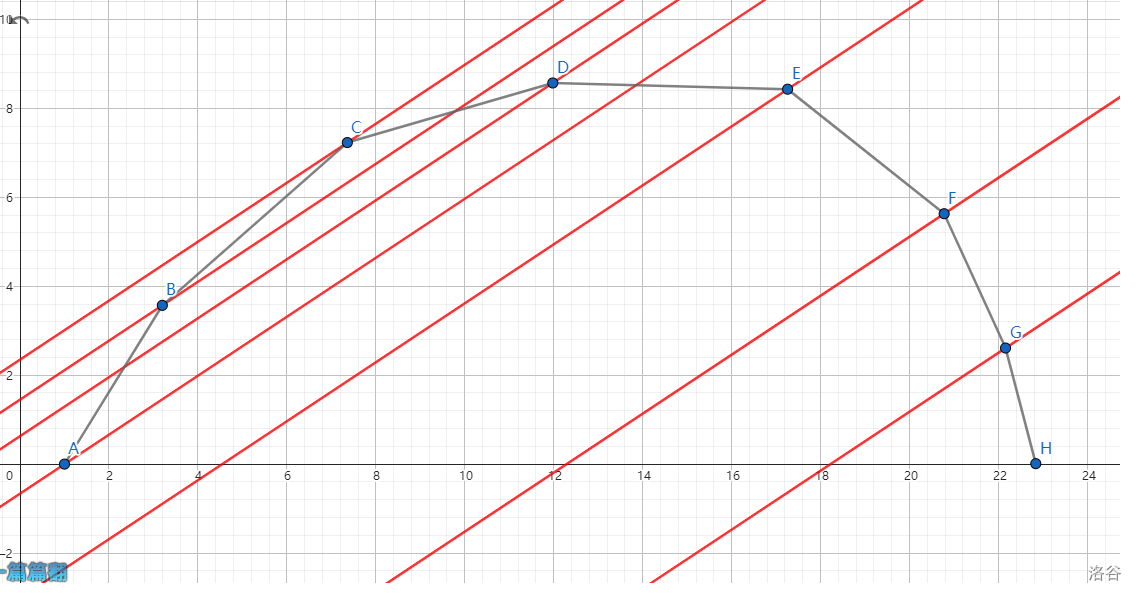
  這個也是上凸殼哦。
  會發(fā)現有且僅有過 \(C\) 點的那條直線與這個凸殼相切,我們稱這個 \(C\) 點為斜率為 \(k\) 的直線與這個上凸殼的切點。
  切點的性質是:他所確定的直線(眾所周知一點和斜率可以確定一條直線)是所有直線中截距最大的。
  下凸殼我們也有類似的結論，把截距最大改成最小即可。

適用場景

斜率優(yōu)化用于解決dp轉移方程中涉及到 \(i,j\) 的乘積項的轉移，先講它的一般形式以及解決方法再放例題。

假設我們現在有這么一個轉移方程:

其中,\(F1,F2,F3,F4\)是一些函數，\(A\) 是一個常量。
\(F1,F2,F3,F4\) 則是一些關于 \(i,j\) 的表達式，因題目而異，注意 \(F1(j),F4(j)\) 只跟 \(j\) 有關，\(F2(i),F3(i)\) 只跟 \(i\) 有關。

我們可以先把與 \(j\) 無關的拉出來，放到 min 外面。

會變得更加美觀，這樣下面我們就不去管后面那一坨東西了。

然后就是斜率優(yōu)化的精髓，對于一個決策點 \(j\),當用他去轉移 \(i\) 時，我們可以把 min 去掉，會得到:

移項:

我們把 \(-F3(i)\) 當作直線的斜率 \(k\),把 \(dp[i]\) 當作直線的截距 \(b\),把 \((F4(j),dp[j] + F1(j))\) 當作直角坐標系的一個點,那相當于這條直線 \(y=kx+b\) 要經過這個點。
因為我們要求的是 \(dp[i]\),也就是 \(b\), 移項得到 \(b = y - kx\),所以我們如果知道斜率和這條直線經過的點就可以知道截距了。
所以問題變成平面上有若干形如 \((F4(j),dp[j] + F1(j))\) 的點，現在要去用一條斜率為 \(k=-F3(i)\) 的直線去切這些點，求最小的截距。

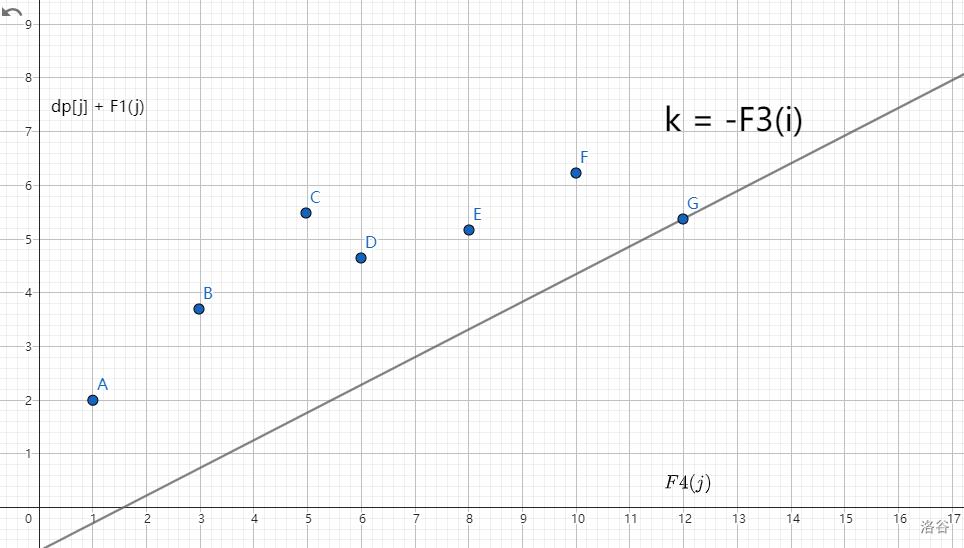
也就是需要將這條直線從下往上平移，第一個切到的點就是我們要的點，比如上圖中是 \(G\) 點。

那怎么快速求出第一個切到的點呢，我們來看上圖中 \(B,C,D\) 這三個點：

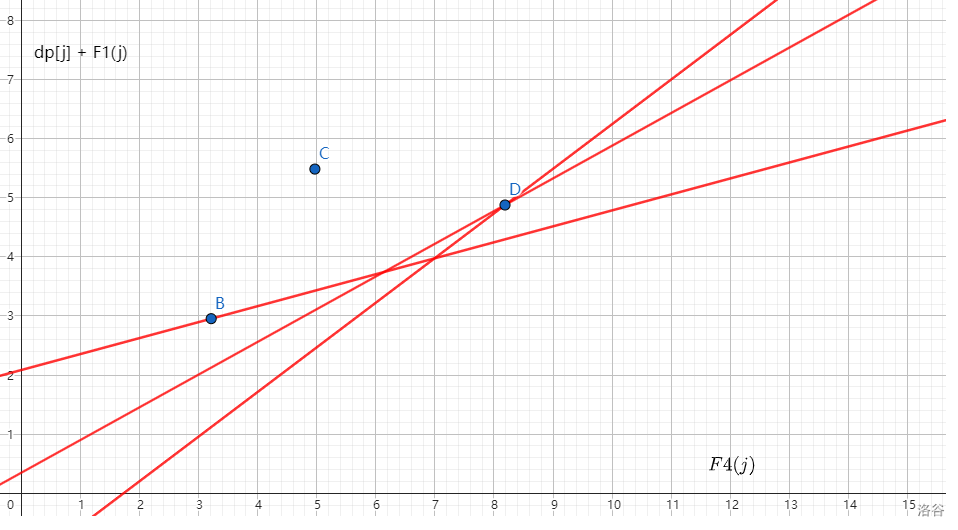
會發(fā)現不管斜率是多少，都切不到 \(C\) 點，所以這種上凸的形狀中間的點是沒用的,也就是說一個點 \(j_2\) 要成為決策點，假設他前面和后面的點是 \(j_1,j_3\)，他的必要不充分條件是:

這個判斷條件如果想簡便可以直接用 long double 存，也可以十字相乘，這樣可以避免精度損失帶來的誤判，因為使用這種方法的斜率優(yōu)化的題基本都會滿足 \(j\) 的橫坐標的函數 \(F4(j)\) 是單調的(不然點出現的順序就不是按照 \(j\) 從小到大了)，所以不用擔心分母出現負數的情況。如果不滿足 \(F4(j)\) 單調就要考慮別的做法了。具體見拓展。
所以說我們要維護的是一個下凸殼，這可以單調隊列來維護，也就是每次加入一個點就判斷一下棧頂的兩個點和新加的這個點是否滿足上述式子(新加的點是 \(j_3\) )，不滿足就不斷彈隊尾，直到滿足為止。

那維護了下凸殼之后怎么求那個切點呢?
進一步發(fā)現性質，如果一個點滿足他之前線段的斜率都小于 \(k=-F3(i)\),后面線段的斜率都大于 \(k=-F3(i)\),那么這個點就是切點,如下圖:

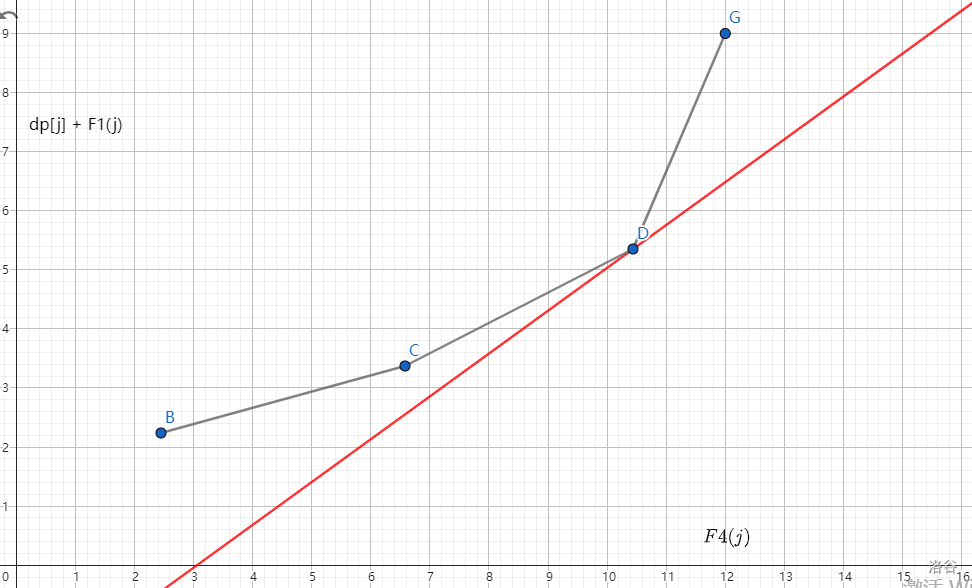
因為下凸殼的點之間的線段的斜率滿足單調性，所以這顯然是可以二分的(這也就意味著你的單調隊列要手寫，因為要查詢棧中元素)。這是最普遍的解法，時間復雜度 \(O(n \log n)\)。
那有些時候不能帶 \(log\) 怎么辦呢？下面的例題會有不帶 \(log\) 的解法（\(O(n)\) 解法并不是每種斜率優(yōu)化的題都適用的）。

當然對于 dp 轉移方程里是 max 的，維護上凸殼即可，結論類似。

例題

所有初學斜率優(yōu)化的應該都是從"任務安排" 這道題開始的吧。

任務安排

弱化版是不用斜率優(yōu)化的。
設 \(f[i][j]\) 表示前 \(i\) 個任務分成 \(j\) 段的最小花費。
\(f[i][j]=min_{0\le j \le i-1}(f[k][j-1] + s + (S1[i]+s\times j)\times (S2[i]-S2[k]))\)。
\(S1\) 是 \(t\) 的前綴和,\(S2\) 是 \(F\) 的前綴和。
這樣是 \(O(n^3)\) 的。

回顧"我的動態(tài)規(guī)劃題單2"中"關路燈"那題，
考慮將 \(s\) 的費用提前計算，只考慮當前這批任務對后面的影響，這樣就可以不去記錄段數 \(j\) 了。
\(f[i]=min_{0\le j \le i-1}(f[j] + S1[i]\times(S2[i]-S2[j]) + s\times (S2[n]-S2[j]))\)。

時間復雜度\(O(n^2)\)。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=1e5+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,s,t[N],F[N],f[N],S1[N],S2[N];
signed main(){
	n=read(),s=read();
	for(int i=1;i<=n;i++){
		t[i]=read(),F[i]=read();	
		S1[i]=S1[i-1]+t[i];
		S2[i]=S2[i-1]+F[i];
	} 
	memset(f,0x3f,sizeof f);
	f[0]=0;
	for(int i=1;i<=n;i++){
		for(int j=0;j<i;j++){
			f[i]=min(f[i],f[j] + S1[i]*(S2[i]-S2[j]) + s*(S2[n]-S2[j]));   
		}
	}
	printf("%lld\n",f[n]);
	return 0;
}

任務安排2

\(f[i]=min_{0\le j \le i-1}(f[j] + S1[i]\times(S2[i]-S2[j]) + s\times (S2[n]-S2[j]))\)。

按照上述所說的套路，把式子改寫一下，只跟 \(j\) 有關和只跟 \(i\) 有關的拎出來:
\(f[i]=min_{0\le j \le i-1}(f[j] - (s+S1[i])\times S2[j]) + s\times S2[n] + S1[i]\times S2[i]\)。
不管后面那一坨，去掉 \(min\) 寫成 \(y=kx+b\) 的形式:
\((s+S1[i])\times S2[j] + f[i] = f[j]\)。
所以就用一條斜率為 \((s+S1[i])\) 的直線去切這些形如 \((S2[j] , f[j])\) 的點。
維護出下凸殼之后，注意到因為 \(t_i\) 都是正數，所以斜率 \((s+S1[i])\) 隨著 \(i\) 的增大而增大，那根據切點的判定條件，切點也是一定右移的，所以只保留斜率大于 \((s+S1[i])\) 的部分即可。
所以就有了一下 \(O(n)\) 的做法:

1. 用單調隊列替換掉單調棧（如果你的斜率優(yōu)化用單調棧寫的話）。
2. 對于 \(i\),把隊頭那些斜率 \(\le (s+S1[i])\) 的線段 pop 掉，這樣隊頭的點就是要求的切點。
3. 取出隊頭轉移。
4. 加入 \(i\),并維護下凸殼。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=3e5+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,s,t[N],c[N],f[N],S1[N],S2[N];
int dq[N],l,r;  //單調隊列 
int x(int j){return S2[j];}  //橫坐標
int y(int j){return f[j];}  //縱坐標 
signed main(){
	n=read(),s=read();
	for(int i=1;i<=n;i++){
		t[i]=read(),c[i]=read();	
		S1[i]=S1[i-1]+t[i];
		S2[i]=S2[i-1]+c[i];
	}
	memset(f,0x3f,sizeof f);
	f[0]=0;
	l=1,r=0; //初始化空的單調隊列 
	dq[++r]=0;
	for(int i=1;i<=n;i++){
		while( l<r && ( y(dq[l+1]) - y(dq[l]) ) <= (s + S1[i]) * ( x(dq[l+1]) - x(dq[l]) ) ) l++;    //注意是 l<r 而不是 l<=r,因為起碼要有兩個點才是線段 
		int j=dq[l];
		f[i]=f[j] + S1[i]*(S2[i]-S2[j]) + s*(S2[n]-S2[j]);  //這里就用原來的式子就好了,新的那個太大便了 
		while( l<r && ( y(dq[r]) - y(dq[r-1]) ) * ( x(i) - x(dq[r]) ) >= ( y(i) - y(dq[r]) ) * ( x(dq[r]) - x(dq[r-1]) ) ) r--;    //維護凸殼 
		dq[++r]=i;
	}
	
	printf("%lld\n",f[n]);
	return 0;
}

[SDOI2012] 任務安排

題面都是一樣的。

這里 \(t_i\) 可能是負數，所以 \((s+S1[i])\) 不一定單調。
所以求切點要二分，這里還是用的單調隊列，其實單調棧也可以。
時間復雜度 \(O(n \log n)\)。
要注意的是，這里 \(c_i\) 可以等于 \(0\),也就是說也就是會出現橫坐標相同的兩個點，那么有可能出現原先的斜率是 \(inf\)(即與 \(x\) 軸垂直，但是后面那個在前面那個上面)，加進來一個后變成 \(-inf\)(加進來的在原來隊尾的下面)，但它們的斜率在比較時是一樣，如果不把前面那個彈掉，就不滿足斜率單調遞增了，所以在維護下凸殼時，\(=\) 的情況也要把隊尾彈掉(代碼中也有注釋）。

code

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=3e5+5;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}
int n,s,t[N],c[N],f[N],S1[N],S2[N];
int dq[N],l,r;  //單調隊列 
int x(int j){return S2[j];}  //橫坐標
int y(int j){return f[j];}  //縱坐標 
int Binary_search(int K){
	int L=l,R=r,mid,res=r;  //二分找第一個滿足它后面的線段的斜率比 s+S1[i] 大的點y 
	while(L<=R){
		mid=(L+R)>>1;
		if(mid<r && y(dq[mid+1]) - y(dq[mid]) > K * ( x(dq[mid+1]) - x(dq[mid]) )) R=mid-1,res=mid;
		else L=mid+1;
	}
	return dq[res];
}
signed main(){
	n=read(),s=read();
	for(int i=1;i<=n;i++){
		t[i]=read(),c[i]=read();	
		S1[i]=S1[i-1]+t[i];
		S2[i]=S2[i-1]+c[i];
	}
	memset(f,0x3f,sizeof f);
	f[0]=0;
	l=1,r=0; //初始化空的單調隊列 
	dq[++r]=0;
	for(int i=1;i<=n;i++){
		int j=Binary_search(s+S1[i]);
		f[i]=f[j] + S1[i]*(S2[i]-S2[j]) + s*(S2[n]-S2[j]); 
		while( l<r && ( y(dq[r]) - y(dq[r-1]) ) * ( x(i) - x(dq[r]) ) >= ( y(i) - y(dq[r]) ) * ( x(dq[r]) - x(dq[r-1]) ) ) r--;    //維護凸殼 
		/*
			這邊取等號是因為 ti 可以=0，也就是會出現橫坐標相同的兩個點，那么有可能出現原先的斜率是 inf(即與 x 軸垂直，但是后面那個在前面那個上面)，
			加進來一個后變成 -inf，但它們的斜率表示出來是一樣，如果不把前面那個彈掉，就不滿足斜率單調遞增了。 
		*/ 
		dq[++r]=i;
	}
	
	printf("%lld\n",f[n]);
	return 0;
}

拓展

如果對于任務安排這題，\(Ti,Ci\) 都可能是負數怎么辦?，即如果這些點的橫坐標不一定按照 \(j\) 單調遞增怎么辦?
這個時候我們換種角度考慮這個式子：

把 \((F3(i),dp[i])\) 看成是一個點，那就是有若干條斜率為 \(F4(j)\) 截距為 \(dp[j]+F1(j)\) 的直線，問 \(x=F3(i)\) 這條豎線與這些直線交點的縱坐標的最大/最小值。
可以用李超樹輕松維護，復雜度為 \(O(n\log n)\)。