簡介
貝葉斯網絡(Bayesian network),又稱信念網絡(belief network)或是有向無環圖模型(directed acyclic graphical model),是一種概率圖型模型,借由有向無環圖(directed acyclic graphs, or DAGs )中得知一組隨機變量{}及其n組條件概率分配(conditional probability distributions, or CPDs)的性質。一般而言,貝葉斯網絡的有向無環圖中的節點表示隨機變量,它們可以是可觀察到的變量,抑或是隱變量、未知參數等。連接兩個節點的箭頭代表此兩個隨機變量是具有因果關系或是非條件獨立的;而節點中變量間若沒有箭頭相互連接一起的情況就稱其隨機變量彼此間為條件獨立。若兩個節點間以一個單箭頭連接在一起,表示其中一個節點是“因(parents)”,另一個是“果(descendants or children)”,兩節點就會產生一個條件概率值。比方說,我們以表示第i個節點,而
的“因”以
表示,
的“果”以
表示;圖1就是一種典型的貝葉斯網絡結構圖,依照先前的定義,我們就可以輕易的從圖1可以得知:
-
![P_2=\left\{X_4,X_5\right\},C_2=\left\{X_1\right\},P_4=\empty,C_4=\left\{X_2,X_5\right\},P_1=\left\{X_2,X_3\right\}]() ,以及
,以及![C_1=\empty]()
圖 1
大部分的情況下,貝葉斯網絡適用在節點的性質是屬于離散型的情況下,且依照此條件概率寫出條件概率表,寫出條件概率表后就很容易將事情給條理化,且輕易地得知此貝葉斯網絡結構圖中各節點間之因果關系;但是條件概率表也有其缺點:若是節點
是由很多的“因”所造成的“果”,如此條件概率表就會變得在計算上既復雜又使用不便。
數學定義
令G = (I,E)表示一個有向無環圖(DAG),其中I代表圖形中所有的節點的集合,而E代表有向連接線段的集合,且令X = (Xi)i ∈ I為其有向無環圖中的某一節點i所代表之隨機變量,若節點X的聯合概率分配可以表示成:
則稱X為相對于一有向無環圖G 的貝葉斯網絡,其中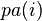 表示節點i之“因”。
表示節點i之“因”。
對任意的隨機變量,其聯合分配可由各自的局部條件概率分配相乘而得出:
依照上式,我們可以將一貝葉斯網絡的聯合概率分配寫成:
-
![\mathrm P(X_1=x_1, \ldots, X_n=x_n) = \prod_{i=1}^n \mathrm P(X_i=x_i \mid X_j=x_j]() , 對每個相對于Xi的“因”變量Xj 而言)
, 對每個相對于Xi的“因”變量Xj 而言)
上面兩個表示式之差別在于條件概率的部分,在貝葉斯網絡中,若已知其“因”變量下,某些節點會與其“因”變量條件獨立,只有與“因”變量有關的節點才會有條件概率的存在。如果聯合分配的相依數目很稀少時,使用貝氏函數的方法可以節省相當大的存儲器容量。舉例而言,若想將10個變量其值皆為0或1存儲成一條件概率表型式,一個直觀的想法可知我們總共必須要計算 個值;但若這10個變量中無任何變量之相關“因”變量是超過三個以上的話,則貝葉斯網絡的條件概率表最多只需計算
個值;但若這10個變量中無任何變量之相關“因”變量是超過三個以上的話,則貝葉斯網絡的條件概率表最多只需計算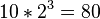 個值即可!另一個貝式網絡優點在于:對人類而言,它更能輕易地得知各變量間是否條件獨立或相依與其局部分配(local distribution)的型態來求得所有隨機變量之聯合分配。
個值即可!另一個貝式網絡優點在于:對人類而言,它更能輕易地得知各變量間是否條件獨立或相依與其局部分配(local distribution)的型態來求得所有隨機變量之聯合分配。
馬爾可夫毯(Markov blanket)
馬爾科夫毯,是滿足如下特性的一個最小特征子集:一個特征在其馬爾科夫毯條件下,與特征域中所有其他特征條件獨立。設特征T的馬爾科夫毯為MB(T),則上述可表示為:
P(T | MB(T)) = P(T | Y, MB(T))
其中Y為特征域中的所有非馬爾科夫毯結點。這是馬爾科夫毯的最直接的定義。關于某一特征的馬爾科夫毯在貝葉斯網絡中的表現形式是該特征(即該結點)的父結點、子結點以及子結點的父結點。
舉例說明
假設有兩個服務器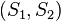 ,會傳送數據包到用戶端 (以U表示之),但是第二個服務器的數據包傳送成功率會與第一個服務器傳送成功與否有關,因此此貝葉斯網絡的結構圖可以表示成如圖2的型式。就每個數據包傳送而言,只有兩種可能值:T(成功) 或 F(失敗)。則此貝葉斯網絡之聯合概率分配可以表示成:
,會傳送數據包到用戶端 (以U表示之),但是第二個服務器的數據包傳送成功率會與第一個服務器傳送成功與否有關,因此此貝葉斯網絡的結構圖可以表示成如圖2的型式。就每個數據包傳送而言,只有兩種可能值:T(成功) 或 F(失敗)。則此貝葉斯網絡之聯合概率分配可以表示成:
圖 2
此模型亦可回答如:“假設已知用戶端成功接受到數據包,求第一服務器成功發送數據包的概率?”諸如此類的問題,而此類型問題皆可用條件概率的方法來算出其所求之發生概率:
該例中網絡的結構已知,只需根據觀測值得到概率表,再根據概率表及聯合概率公式計算
求解方法
以上例子是一個很簡單的貝葉斯網絡模型,但是如果當模型很復雜時,這時使用枚舉式的方法來求解概率就會變得非常復雜且難以計算,因此必須使用其他的替代方法。一般來說,貝氏概率有以下幾種求法:
精確推理
- 枚舉推理法(如上述例子)只適用于簡單的網絡
- 變量消元算法(variable elimination)
隨機推理(蒙特卡洛方法)
- 直接取樣算法
- 拒絕取樣算法
- 概似加權算法
- 馬爾可夫鏈蒙特卡洛算法(Markov chain Monte Carlo algorithm)
在此,以馬爾可夫鏈蒙特卡洛算法為例,又馬爾可夫鏈蒙特卡洛算法的類型很多,故在這里只說明其中一種Gibbs sampling的操作步驟: 首先將已給定數值的變量固定,然后將未給定數值的其他變量隨意給定一個初始值,接著進入以下迭代步驟:
- (1)隨意挑選其中一個未給定數值的變量
- (2)從條件分配
![P(X_i|\text{Markovblanket}(X_i))]() 抽樣出新的
抽樣出新的![X_i]() 的值,接著重新計算
的值,接著重新計算
-
![P(X_i|\text{Markovblanket}(X_i))=\alpha P(X_i|\text{parents}(X_i)) \times \prod_{Y_i \in \text{children}(X_i)} \text{parent}(Y_i)]()
當迭代退出后,刪除前面若干筆尚未穩定的數值,就可以求出 的近似條件概率分配。馬爾可夫鏈蒙特卡洛算法的優點是在計算很大的網絡時效率很好,但缺點是所抽取出的樣本并不具獨立性。
當貝葉斯網絡上的結構跟參數皆已知時,我們可以通過以上方法來求得特定情況的概率,不過,如果當網絡的結構或參數未知時,我們必須借由所觀測到的數據去推估網絡的結構或參數,一般而言,推估網絡的結構會比推估節點上的參數來的困難。依照對貝葉斯網絡結構的了解和觀測值的完整與否,我們可以分成下列四種情形:
| 結構 | 觀測值 | 方法 |
|---|---|---|
| 已知 | 完整 | 最大似然估計法 (MLE) |
| 已知 | 部份 | EM 算法 Greedy Hill-climbing method |
| 未知 | 完整 | 搜索整個模型空間 |
| 未知 | 部份 | 結構算法 EM 算法 Bound contraction |
以下就結構已知的部分,作進一步的說明。
1. 結構已知,觀測值完整:
此時我們可以用最大似然估計法(MLE)來求得參數。其對數概似函數為
其中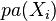 代表
代表 的因變量,
的因變量, 代表第
代表第 個觀測值,N代表觀測值數據的總數。
個觀測值,N代表觀測值數據的總數。
以圖二當例子,我們可以求出節點U的最大似然估計式為
由上式就可以借由觀測值來估計出節點U的條件分配。如果當模型很復雜時,這時可能就要利用數值分析或其它最優化技巧來求出參數。
2. 結構已知,觀測值不完整(有遺漏數據):
如果有些節點觀測不到的話,可以使用EM算法(Expectation-Maximization algorithm)來決定出參數的區域最佳概似估計式。而EM算法的的主要精神在于如果所有節點的值都已知下,在M階段就會很簡單,如同最大似然估計法。而EM算法的步驟如下:
(1)首先給定欲估計的參數一個起始值,然后利用此起始值和其他的觀測值,求出其他未觀測到節點的條件期望值,接著將所估計出的值視為觀測值,將此完整的觀測值帶入此模型的最大似然估計式中,如下所示(以圖二為例):
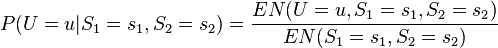
其中 代表在目前的估計參數下,事件x 的條件概率期望值為
代表在目前的估計參數下,事件x 的條件概率期望值為
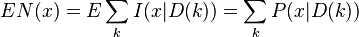
(2)最大化此最大似然估計式,求出此參數之最有可能值,如此重復步驟(1)與(2),直到參數收斂為止,即可得到最佳的參數估計值。
本文引自http://blog.csdn.net/memory513773348/article/details/16973807


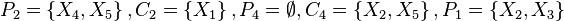 ,以及
,以及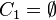

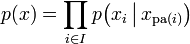
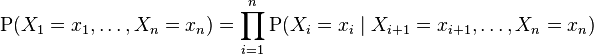
 , 對每個相對于Xi的“因”變量Xj 而言)
, 對每個相對于Xi的“因”變量Xj 而言)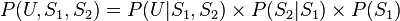

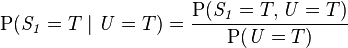
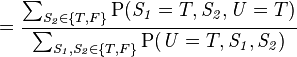
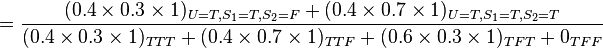

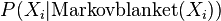 抽樣出新的
抽樣出新的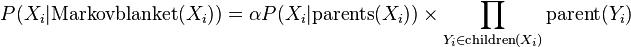

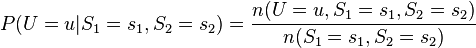

 浙公網安備 33010602011771號
浙公網安備 33010602011771號