建議參考：

http://www.rzrgm.cn/chilema/articles/14506922.html

上面鏈接作為輔助閱讀之用。

引自：

https://blog.csdn.net/lxl1307/article/details/142518676

（2）浮點數存的過程
IEEE754規定：
對于32位的浮點數，最高的1位存儲符號位S，接著的8位存儲指數E，剩下的23位存儲有效數字M對于64位的浮點數，最高的1位存儲符號位S，接著的11位存儲指數E，剩下的52位存儲有效數字M

對于M：

由于1≤M<2 ，所以M可以寫成 1.xxxxxx 的形式，其中 xxxxxx 表示小數部分。IEEE754規定，在計算機內部保存M時，默認這個數的第?位總是1，因此可以被舍去，只保存后面的xxxxxx部分，這樣做的目的是節省1位有效數字。以32位浮點數為例，留給M只有23位，將第一位的1舍去以后，相當于可以保存24位有效數字

對于E:

E為?個無符號整數，如果E為8位，它的取值范圍為0_{255；如果E為11位，它的取值范圍為0}2047。但是，我們知道，科學計數法中的E是可以出現負數的，所以IEEE754規定，存入內存時E的真實值必須再加上?個中間數，對于8位的E，這個中間數是127；對于11位的E，這個中間數是1023

（3）浮點數取的過程
E不全為0或不全為1：
指數E的計算值減去127（或1023），得到真實值，再將有效數字M前加上第?位的1

E全為0：
浮點數的指數E等于1-127（或者1-1023）即為真實值，有效數字M不再加上第?位的1，而是還原為0.xxxxxx的小數。這樣做是為了表示±0，以及接近于0的很小的數字
E全為1：
如果有效數字M全為0，表示±無窮大（正負取決于符號位s）

（4）解釋下面程序的運行結果

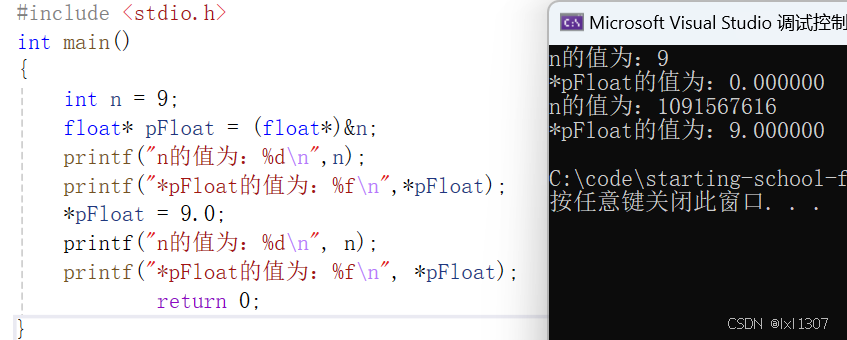
n在內存中的儲存為00000000 00000000 00000000 00001001

以浮點數的形式打印，則S為0，E為00000000，M為00000000000000000001001

由于E為全0，所以E為1-127，V=(-1)^{0×0.00000000000000000001001×2}(-126)=1.001×2^(-146)，用十進制表示是0.000000

*pFloat浮點數的二進制表示為V=（-1)^0*1.001*23,在內存中的儲存為0 10000010 00100000 000000000000000

以整數的形式打印，補碼為01000001 00010000 00000000 00000000 ，原碼同，以十進制的形式打印，為1091567616

階碼：E

尾數：M

二進制數：
01000001000100000000000000000000

該二進制數為浮點數（float）9.0，但是因為用int類型進行表示，則按照int類型的表示方法進行讀取；
由于符號為為0，代表為正數，因此原碼、反碼、補碼格式一致；
內存中該二進制數的表示為補碼形式，最后輸出補碼形式對應的數，即為 1091567616

————————————————
版權聲明：本文為CSDN博主「lxl1307」的原創文章，遵循CC 4.0 BY-SA版權協議，轉載請附上原文出處鏈接及本聲明。
原文鏈接：https://blog.csdn.net/lxl1307/article/details/142518676