題目分析
仔細閱讀題目,可知題目要求的是對于每個 \(a_i\) 的 \(\sum\limits_{j=1}^ng(a_i,a_j)\) 。再結(jié)合 \(g(a,b)\) 的定義,可知,對于 \(a_i\) 來說,我們需要計算 \(a_i\) 與 \(a_1\sim a_n\) 構(gòu)成的 \(n\) 組數(shù)對的 \(g(a_i,a_j)\) 的總和。對于 \(g(a,b)\) 的值,則是 \([\min(a,b),\max(a,b)]\) 中的最小 \(f(c)\) 的值,當(dāng)前 \(c\in [\min(a,b),\max(a,b)]\)。對于 \(f(c)\) 的作用則是返回將小數(shù) \(c\) 變成整數(shù)的乘 \(10\) 的次數(shù),即 \(c\) 的小數(shù)部分的位數(shù)。題目描述的比較繞,需要耐心將公式之間的關(guān)系捋清楚。
接下來思考如何計算 \(g(a,b)\)。我們分情況進行討論,為方便描述我們設(shè) \(a\le b\)。
- 兩個數(shù)的整數(shù)部分不同。
當(dāng)整數(shù)部分不相同時,在 \([a,b]\) 中一定可以存在一個整數(shù) \(c\) ,當(dāng) \(c\) 為整數(shù)時,\(f(c)=0\)。所以整數(shù)部分不相同,\(g(a,b)=0\)。
-
兩個數(shù)的整數(shù)部分相同。當(dāng)整數(shù)部分相同時,考慮小數(shù)部分。可以分成三種情況:
-
小數(shù)部分完全不一樣。
如 \(11.123\) 和 \(11.231\) 對應(yīng)的 \(c=11.2\),\(f(c)=1\)。也就是較小的數(shù)值保留1位小數(shù)再加 \(0.1\) 就好,這樣乘 \(10^1\) 就能成為整數(shù)。
-
部分前綴相同。
如 \(11.12345\) 和 \(11.12388\) 對應(yīng)的 \(c=11.1235\),\(f(c)=4\)。也就是先找 \(a\) 和 \(b\) 的最大公共前綴,再往后一位,找一個在兩者范圍內(nèi)的數(shù)字即可,若小數(shù)點后最大公共前綴長度為 \(k\) 則乘 \(10^{k+1}\) 就能成為整數(shù)。
-
較小的數(shù)字是較大數(shù)字的前綴。
如 \(11.123\) 和 \(11.123456\) 對應(yīng)的 \(c=11.123\),\(f(c)=3\)。也就是較小的那個數(shù)字的小數(shù)位數(shù),若較小數(shù)字的小數(shù)位置為 \(k\) 則乘 \(10^k\) 就能成為整數(shù)。
-
此時我們可以發(fā)現(xiàn),問題是圍繞著公共前綴展開的。對于小數(shù)的公共前綴,我們可以將小數(shù)視為字符串進行存儲與使用,就將問題轉(zhuǎn)換了字符串的公共前綴問題,這類問題使我們聯(lián)想到字典樹,可以考慮使用字典樹解決它。
以樣例2為例,講解字典樹解法思路。
8
1.1145
1.114
1.1145
1.514
1.19198
1.1154
1.114
1.1145
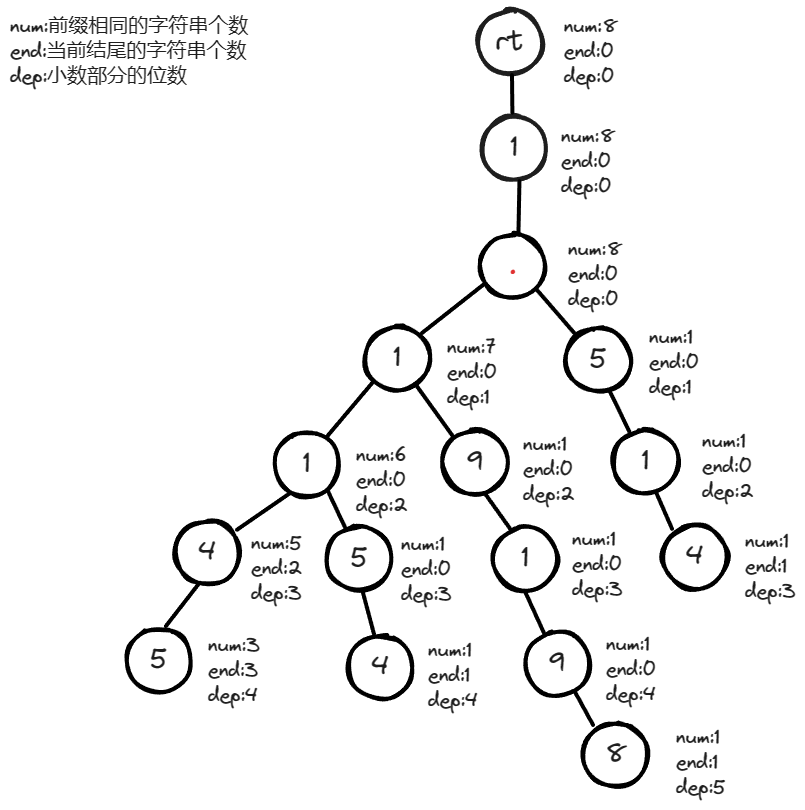
下圖為建立好的字典樹。
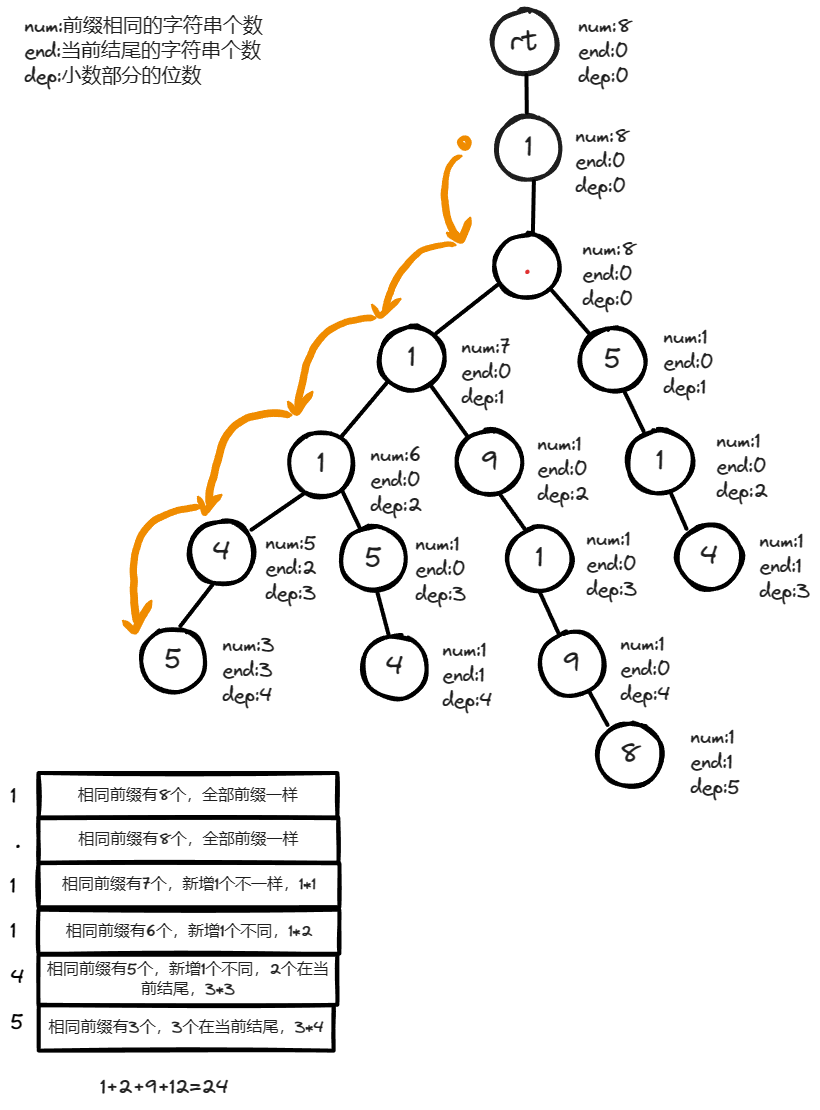
查找數(shù)值 \(1.1145\) 的答案過程。
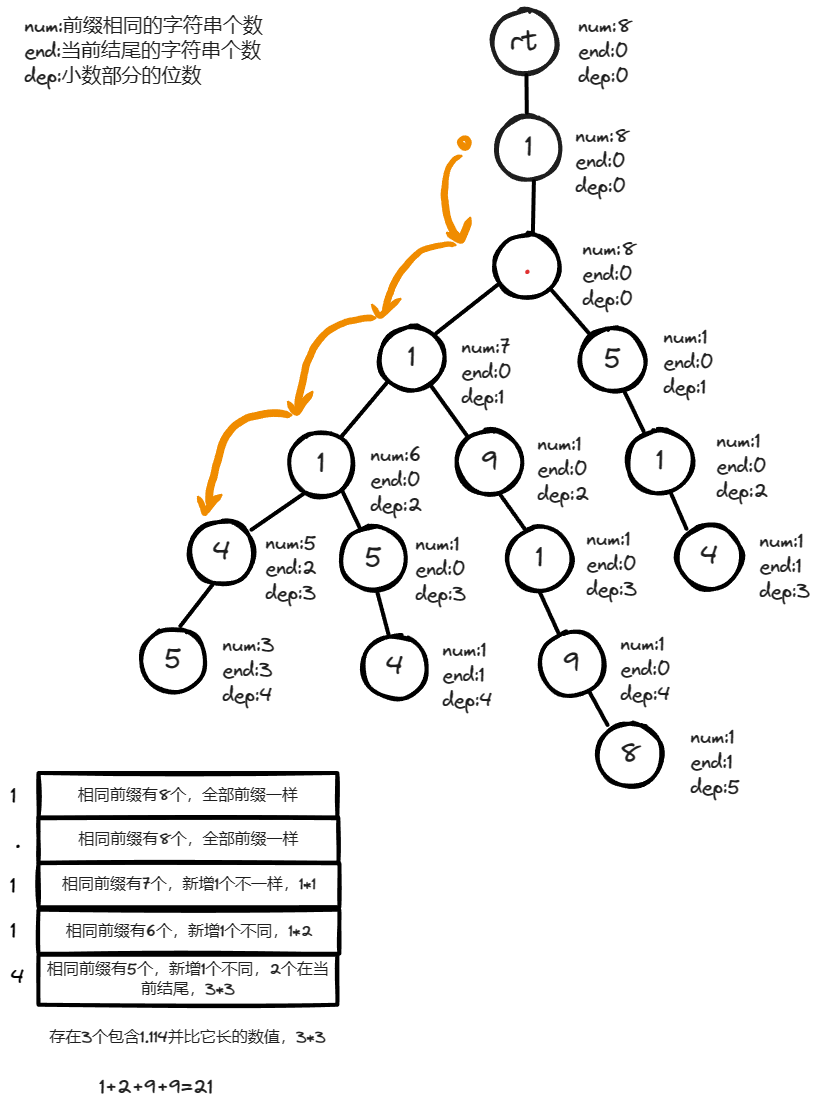
查找數(shù)值 \(1.114\) 的答案過程。
查找數(shù)值 \(1.514\) 的答案過程。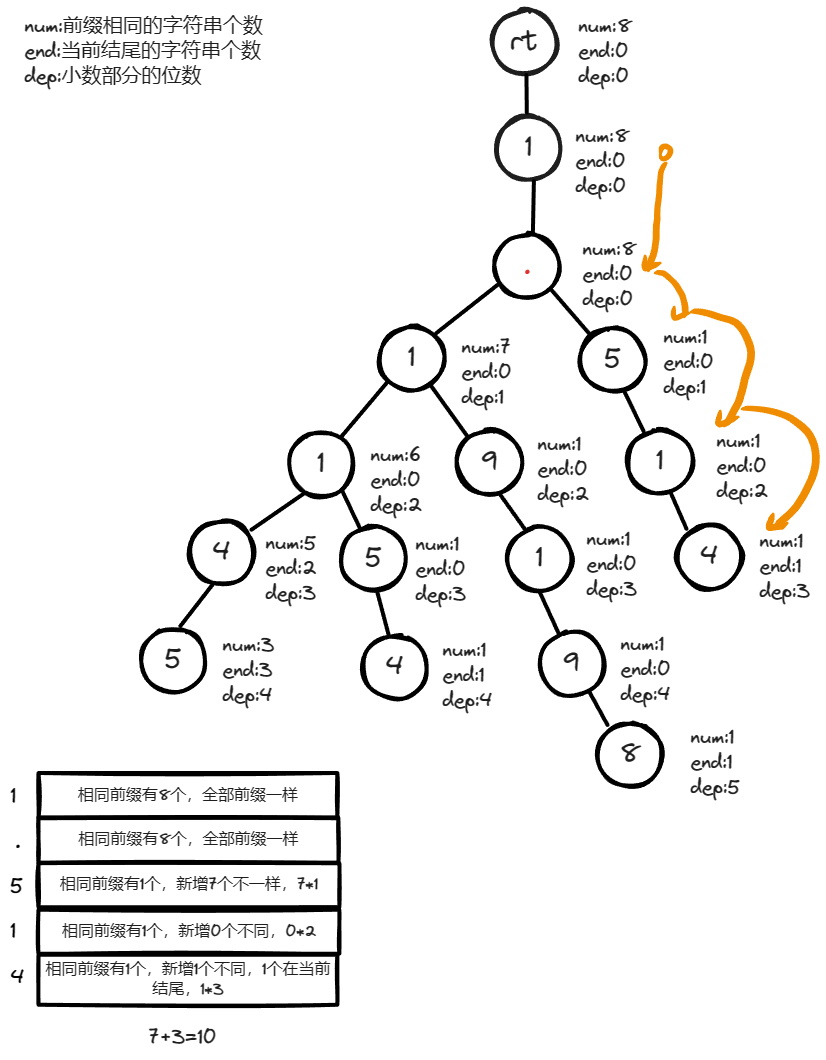
模擬過程中可發(fā)現(xiàn),在遍歷字典樹的過程中,我們計算新增的不同前綴的元素個數(shù)與當(dāng)前結(jié)尾的元素個數(shù),它們成為整數(shù)的答案為當(dāng)前小數(shù)位數(shù)。另外,在遍歷結(jié)束后需要考慮和計算以當(dāng)前數(shù)字為前綴且又比它長的數(shù)字個數(shù),詳細可查看尋找數(shù)值 \(1.114\) 的過程。
代碼實現(xiàn)
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
const int N = 1e5 + 5;
const int M = 3e6 + 5;
int n, tot, zs;
string str[N];
struct node {
int son[11];
// 前綴相同的字符串個數(shù)、以該節(jié)點結(jié)尾的字符串個數(shù)、小數(shù)部分的位數(shù)
int num, end, dep;
} trie[M];
int toNum[256];
void init() {
for (int i = 0; i < 10; i++) {
toNum[i + '0'] = i;
}
toNum['.'] = 10;
}
void insert(string s) { // 字典樹插入
int len = s.size();
int u = 0;
int dot = -1; // 小數(shù)點位置
trie[u].num++; // 記錄字符串總數(shù)
for (int i = 0; i < len; i++) {
int ch = toNum[s[i]];
if (!trie[u].son[ch]) trie[u].son[ch] = ++tot;
u = trie[u].son[ch];
trie[u].num++;
if (ch == 10) dot = i; // 記錄小數(shù)點的位置
if (dot != -1) trie[u].dep = i - dot; // 更新小數(shù)部分對應(yīng)的位數(shù)
}
trie[u].end++;//記錄該處結(jié)尾的數(shù)字個數(shù)
}
int findStr(string s) {
// 整數(shù)部分不一樣,f(c)為0
// 整數(shù)部分相同時考慮小數(shù)部分的最大公共前綴
int len = s.size();
int sum = 0, re = trie[0].num; // re-剩余前綴相同的字符串?dāng)?shù)量
int u = 0;
for (int i = 0; i < len; i++) {
int ch = toNum[s[i]];
u = trie[u].son[ch];
// num=新增的前綴不同的字符串?dāng)?shù)量 + 以該節(jié)點結(jié)尾的字符串?dāng)?shù)量
int num = re - trie[u].num + trie[u].end;
sum += num * trie[u].dep; // 更新總和
re -= num;
}
// 處理前綴與s相同,但又比s長的字符串
sum += (trie[u].num - trie[u].end) * trie[u].dep;
return sum;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
init();
string s;
char c;
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> str[i];
insert(str[i]);
}
for (int i = 1; i <= n; i++) {
cout << findStr(str[i]) << '\n';
}
return 0;
}



 浙公網(wǎng)安備 33010602011771號
浙公網(wǎng)安備 33010602011771號