奇異值分解
概述
??奇異值分解(Singular Value Decomposition,SVD)是線性代數中一種重要的矩陣分解方法,區別于只適用于實對稱矩陣的特征分解方法,奇異值分解可對任意實矩陣進行分解。
特征分解
?特征分解(eigendecomposition)又叫譜分解(Spectral decomposition),是把一個矩陣根據其特征值和特征向量分解的過程,只有可以正交化的矩陣才可以進行特征分解。
\(A\)為\(n\)階方陣,若存在\(n\)維非零向量\(x\)使得:
\[Ax = \lambda x \]則稱\(\lambda\)為矩陣\(A\)的特征值,\(x\)為\(A\)屬于\(\lambda\)的特征向量(eigenvector)。
??有了上述定義,接下來討論如何計算一個矩陣的特征值和特征向量。由定義可知:
??其中\(I\)為單位矩陣,顯然上式的推導結果是一個\(n\)元\(n\)次的齊次線性方程組,\(x\)為該方程組的一個非零解,則有$r(A-\lambda I)=r < n \Leftrightarrow |A-\lambda I|=0 \(,其中\)|A-\lambda I|=0\(稱為\)A\(的特征方程,\)|A-\lambda I|\(稱為\)A$的特征多項式。基于此,可得到求解方陣A特征值和特征向量的步驟如下:
1、計算方陣A的特征多項式\(|A-\lambda I|\);
2、求出特征方程\(|A-\lambda I|=0\)的所有根(包括復根和重根),這些根\(\lambda_1,\lambda_2,\cdots,\lambda_n\)即為\(A\)的所有特征值;
3、對于\(A\)的每一個特征值\(\lambda_i(1\leq i\leq n)\),求解齊次線性方程組\((A-\lambda_i I)x=0\),該方程組的每一個非零解都是\(A\)屬于特征值\(\lambda_i\)的特征向量;
??求出矩陣\(A\)的特征值和特征向量后,若矩陣\(A\)有\(n\)個線性獨立的特征向量,那么 \(A\)是可以正交化的,此時 \(A\) 的特征分解為:
其中\(W\)時\(n\)個特征向量所組成的\(n \times n\)維矩陣,\(D\)為以這\(n\)個特征值為主對角線元素的對角陣。
奇異值分解
-
定義
若\(M\)為一個\(m \times n\)階的矩陣,則存在一個分解,使得:
\[M = UDV^T \]其中\(U\)為\(m\)階酉矩陣、\(V\)為\(n\)階酉矩陣、\(D\)為\(m\times n\)的非負實對角矩陣。稱此分解為奇異值分解,一般我們將\(V\)中的每一個特征向量叫做\(M\)的右奇異向量,將\(U\)中的每個特征向量叫做左奇異向量,\(D\)對角線上的元素稱為\(M\)的奇異值,當規定奇異值降序排列時,可唯一確定一個\(D\)。
??有了定義,接下來需要確定奇異值分解的三個矩陣\(U、D、V\)。比較直觀的想法是通過\(M\)來構造一個方陣來進行特征分解,間接計算\(U、D、V\),由于\(MM^T,M^TM\)分別為\(m\times m\)和\(n\times n\)的方陣,則有:
\[\begin{equation} \begin{split} MM^T=UDV^T(UDV^T)^T=UDV^TVD^TU^T = UDD^TU^T=U\sum_1 U^T \\ M^TM = (UDV^T)^TUDV^T=VD^TU^TUDV^T=VDD^TV^T=V\sum_2 V^T \end{split} \end{equation} \]注意到:
\[M = UDV^T \Rightarrow MV = UDV^TV \Rightarrow MV= UD \Rightarrow Mv_i = \delta_iu_i \Rightarrow \delta_i = \frac{Mv_i}{u_i} \]其中,\(v_i,u_i\)分別為\(V,U\)中第\(i\)個特征向量。這個式子提供了一種計算奇異值的方法,另一種思路是結合式(5):
\[\sum = DD^T=D^2 \Rightarrow \delta_i = \sqrt{\lambda_i} \]即,特征值矩陣為奇異值矩陣的平方,故可以通過計算\(M^TM\)的特征值取平方根來計算奇異值。
-
SVD的計算步驟
1.計算\(MM^T\)和\(M^TM\);
2.分別計算\(MM^T\)和\(M^TM\)的特征向量和特征值;
3.\(MM^T\)的特征向量組成\(U\),而\(M^TM\)的特征向量組成\(V\);
4.對\(MM^T\)和\(M^TM\)的非零特征值求平方根,對應上述特征向量的位置,填入對角陣\(D\)的位置;
-
計算示例
??接下來以計算矩陣\(A=\begin{pmatrix}0&1 \\ 1& 1 \\1&0\end{pmatrix}\)的奇異值分解為例,來進一步熟悉:
第一步,先計算\(A\)的兩個轉置積:
\[\begin{equation} \begin{split} &A^TA=\begin{pmatrix} 0 & 1 & 1 \\ 1 & 1 & 0 \end{pmatrix}\begin{pmatrix} 0 & 1 \\ 1 & 1 \\ 1 & 0\end{pmatrix} = \begin{pmatrix}2 & 1 \\ 1& 2\end{pmatrix} \\ &AA^T = \begin{pmatrix}0 & 1 \\ 1 & 1 \\ 1 & 0\end{pmatrix}\begin{pmatrix}0 & 1 &1 \\ 1 & 1 & 0\end{pmatrix}=\begin{pmatrix}1 & 1 & 0 \\ 1 & 2 & 1 \\ 0 & 1 & 1\end{pmatrix} \end{split} \end{equation} \]第二步,分別計算兩個轉置積的特征值和特征向量:
\[\begin{equation} \begin{split} &\color{#F00}{(A^TA-\lambda I)x = 0} \Rightarrow |A^TA-\lambda I|=0 \\ &\Rightarrow \begin{vmatrix} 2-\lambda & 1 \\ 1 & 2-\lambda \end{vmatrix} = 0 \Rightarrow \lambda^2-4\lambda+3=0 \end{split} \end{equation} \]容易得到式(9)中一元二次方程的根為\(\lambda_1 = 3,\lambda_2=1\),當\(\lambda=3\)時,將特征根分別帶入式(1)中,得到:
\[\begin{equation} \begin{split} &&(A^TA-3I)x = 0 \Rightarrow\begin{pmatrix}-1 & 1 \\ 1 & -1\end{pmatrix}x= 0 \Rightarrow\begin{pmatrix}-1 & 1 \\ 1 & -1\end{pmatrix}\begin{pmatrix}x_1 \\ x_2\end{pmatrix}= 0 \\ \end{split} \end{equation} \]此時的單位特征向量為:
\[x_{\lambda=3} = \begin{pmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}}\end{pmatrix} \]同理得到:
\[x_{\lambda=1} = \begin{pmatrix} \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}}\end{pmatrix} \]同理計算\(AA^T\)的特征根和特征向量:
\[\begin{equation} \begin{split} &\lambda_1=3,u_1= \begin{pmatrix} \frac{1}{\sqrt{6}} \\ \frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{6}} \end{pmatrix}; &\lambda_2 = 1,u_2 = \begin{pmatrix} \frac{1}{\sqrt{2}} \\ 0 \\ -\frac{1}{\sqrt{2}} \end{pmatrix}; &\lambda_3 = 0,u_3 = \begin{pmatrix} \frac{1}{\sqrt{3}} \\ -\frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{3}} \end{pmatrix} \end{split} \end{equation} \]第三步,使用兩個轉置積的單位特征向量構造\(U,V\)矩陣:
\[\begin{equation} \begin{split} &U =(u_1,u_2,u_3)= \begin{pmatrix} \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} \\ \frac{2}{\sqrt{6}} & 0 & -\frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{6}} & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} \end{pmatrix} \\ &V^T = (v_1,v_2)^T= \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} \end{split} \end{equation} \]第四步,計算奇異值,直接使用\(\delta_i = \sqrt{\lambda_i}\)計算奇異值并組成對角陣\(D\):
\[D = \begin{pmatrix} \sqrt{3} & 0\\ 0 & 1\\ 0 & 0 \end{pmatrix} \]最終得到矩陣\(A\)的奇異值分解:
\[A= UDV^T =\begin{pmatrix} \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} \\ \frac{2}{\sqrt{6}} & 0 & -\frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{6}} & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} \end{pmatrix}\begin{pmatrix} \sqrt{3} & 0\\ 0 & 1\\ 0 & 0 \end{pmatrix} \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} \]
應用
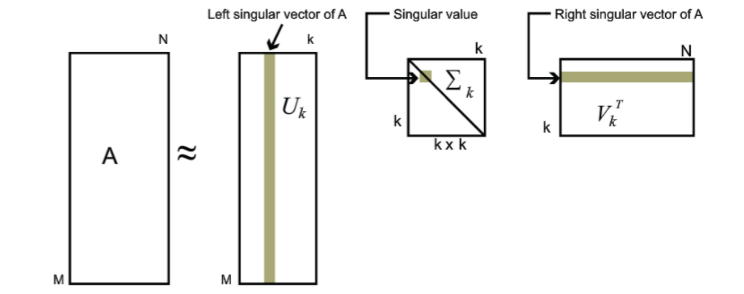
??對于奇異值,它跟我們特征分解中的特征值類似,在奇異值矩陣中也是按照從大到小排列,而且奇異值的減少特別的快,在很多情況下,前10%甚至1%的奇異值的和就占了全部的奇異值之和的99%以上的比例。也就是說,我們也可以用最大的k個的奇異值和對應的左右奇異向量來近似描述矩陣:
這樣處理的好處是,我們可以用三個較小的矩陣\(U_{m \times k},D_{k \times k},V_{k \times n}^T\)來表示一個大矩陣\(A\),如下圖所示,使用三個灰色部分的小矩陣來表示大矩陣。
??由于這個重要的性質,SVD可以用于PCA降維,來做圖片數據壓縮和去噪。也可以用于推薦算法,將用戶和喜好對應的矩陣做特征分解,進而得到隱含的用戶需求來做推薦。同時也可以用于NLP中的算法,比如潛在語義索引(LSI)。
Note:
??需要注意的是,奇異值分解中特征值的求解是比較核心的地方,在工程應用中,往往需要進行奇異值分解都是大矩陣,對這類大矩陣,如果采用上面的方法求解特征值需要花費較多的時間和資源。對此,可以采用乘冪法和反冪法或者QR方法來近似求解矩陣的特征根,在此不做進一步展開,有興趣的讀者可以進一步了解一下。
基本概念說明
-
矩陣的子式
??設有\(m \times n\)矩陣A,在\(A\)中任意取定\(k\)個行和\(k\)個列(\(k \leq \min\{m,n\}\)),位于這些行與列交叉處的元素按原來的相對順序排成一個\(k\)階行列式,稱它為矩陣\(A\)的一個\(k\)階子式,特別地,\(A\)中每一個元素就是\(A\)的一階子式。
對于確定的\(k\),在\(m \times n\)矩陣\(A\)中,總共有\(C_m^k \times C_n^k\)個\(k\)階子式,這些子式的值有的可能是零,也可能不為零,把值不為零的子式稱為非零子式。 -
矩陣的秩
??在\(m\times n\)矩陣\(A\)中,非零子式的最高階數稱為矩陣\(A\)的秩,記為\(r(A)\)或秩規定零矩\((A)\),規定零矩陣的秩為零。
推論1:
\(r(A)=r \Leftrightarrow A\)中所有\(r+1\)階子式(如果有的話)全為零,而\(A\)中至少有一個\(r\)階子式非零。
-
矩陣的譜半徑
??\(A\)為\(n\)階方陣,\(\lambda_i(1\leq i\leq n)\)為其特征值,則\(A\)的譜半徑定義如下:
\[\rho(r) = max\{|\lambda_1|,|\lambda_2|,\dots,|\lambda_n|\} \]即方陣\(A\)的譜半徑為\(A\)特征值中絕對值最大的那個值。
-
正定矩陣
??如果對于所有的非零實系數向量 \(z\),都有 \(z^TAz>0\),則稱矩陣 \(A\) 是正定的。正定矩陣的行列式必然大于0, 所有特征值也必然大于0。相對應的,半正定矩陣的行列式必然 ≥ 0。
-
正交矩陣
??若一個方陣其行與列皆為正交的單位向量(即二者的內積為0),則該方陣為正交矩陣。
-
酉矩陣
??酉矩陣(unitary matrix)是一種特殊的方陣,它滿足\(UU^H=U^HU=I_n\)(\(U^H\)為\(U\)的共軛轉置,其在轉置的基礎上,增加了復數的共軛)。酉矩陣實際上是推廣的正交矩陣(orthogonal matrix);當酉矩陣中的元素均為實數時,酉矩陣實際就是正交矩陣。另一方面,由于\(U^{-1}U=UU^{-1}=I_n\),所以酉矩陣 \(U\)滿足$ U{?1}=UH$;事實上,這是一個矩陣是酉矩陣的充分必要條件。
-
正規矩陣
??同酉矩陣一樣,正規矩陣(normal matrix)也是一種特殊的方陣,它要求在矩陣乘法的意義下與它的共軛轉置矩陣滿足交換律,即\(MM^H=M^HM\)。顯然,復系數的酉矩陣和實系數的正交矩陣都是正規矩陣。
-
譜定理和譜矩陣
??矩陣的對角化是線性代數中的一個重要命題。譜定理(spectral theorem)給出了方陣對角化的一個結論:若矩陣\(M\)是一個正規矩陣,則存在酉矩陣 \(U\),以及對角矩陣 \(\sum\),使得\(M=U\sum U^H\)。也就是說,正規矩陣,可經由酉變換,分解為對角矩陣;這種矩陣分解的方式,稱為譜分解(spectral decomposition)。
參考文章





 浙公網安備 33010602011771號
浙公網安備 33010602011771號