之前學習了隱馬爾可夫模型，現在記錄一下條件隨機場。本文主要參考了《統計學習方法》，如有錯誤，請各位多多指教

1、什么是條件隨機場

首先我們先了解什么是隨機場。

在概率論中，隨機場的定義為：由樣本空間Ω = {0, 1, ..., G ? 1}n取樣構成的隨機變量Xi所組成的S = {X1, ..., Xn}。若對所有的ω∈Ω下式均成立，則稱π為一個隨機場。更直白一點的理解是隨機場是由若干個位置組成的整體，當給每一個位置中按照某種分布隨機賦予一個值之后，其全體就叫做隨機場。就如一句話對他進行詞性標注，先不論對錯，只要對每個詞標注了就形成一個隨機場。

接著我們來了解什么是馬爾科夫隨機場。

先看《統計學習方法》中對馬爾科夫隨機場的定義。

概率無向圖模型，又稱為馬爾可夫隨機場，是一個可以由無向圖表示的聯合概率分布。

圖(graph)是由結點(node)及連接結點的邊(edge)組成的集合。結點和邊分別記作 v 和 e，結點和邊的集合分別記作 V 和 E，圖記作G=(V,E)。無向圖是指邊沒有方向的圖。設有聯合概率分布P(Y)，Y是一組隨機變量。由無向圖G=(V,E)表示概率分布P(Y)，即在圖G中，每個結點 v 表示一個隨機變量Yv；每條邊e表示隨機變量之間的概率依賴關系。

定義：設有聯合概率分布P(Y)由無向圖G=(V,E)表示，在圖G中，結點表示隨機變量，邊表示隨機變量之間的依賴關系。如果聯合概率分布P(Y)滿足成對、局部或全局馬爾可夫性，就稱此聯合概率分布為概率無向圖模型，或馬爾可夫隨機場。

成對、局部或全局馬爾可夫性定義如下：

成對馬爾可夫性：設u和v是無向圖G中任意兩個沒有邊連接的結點，結點u和v分別對應隨機變量Yu和Yv，其他所有結點為O，對應的隨機變量組是YO。成對馬爾可夫性是指給定隨機變量組YO的條件下隨機變量Yu和Yv是條件獨立的，即

 

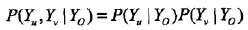
局部馬爾可夫性：設v是無向圖G中任意一個結點，W是與v有邊連接的所有結點，O是v, W以外的其他所有結點。分別表示隨機變量Yv，以及隨機變量組YW和YO。局部馬爾可夫性是指在給定隨機變量組YW的條件下隨機變量Yv與隨機變量組YO是獨立的，即

 

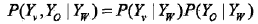
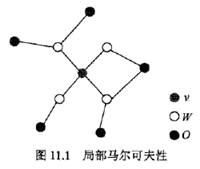
全局馬爾可夫性:設結點集合A, B是在無向圖G中被結點集合C分開的任意結點集合，如圖11.2所示。結點集合A, B和C所對應的隨機變量組分別是YA，YB和YC。全局馬爾可夫性是指給定隨機變量組YC條件下隨機變量組YA，YB是條件獨立的，即

 

 

 

 

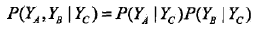
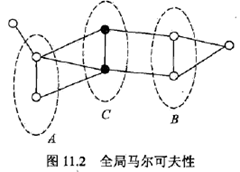
上述成對的、局部的、全局的馬爾可夫性定義是等價的。

這里更直白一點的理解是馬爾科夫隨機場是隨機場的特例，它假設隨機場中某一個位置的賦值僅僅與和它相連的位置的賦值有關，和與其不相連的位置的賦值無關。

條件隨機場

條件隨機場是給定隨機變量X條件下，隨機變量Y的馬爾可夫隨機場。這里主要介紹定義在線性鏈上的特殊的條件隨機場，稱為線性鏈條件隨機場。

定義：設X與Y是隨機變量，P(Y | X)是在給定X的條件下Y的條件概率分布。若隨機變量Y構成一個由無向圖G=(V,E)表示的馬爾可夫隨機場，即

 

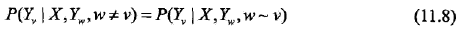
對任意結點v成立，則稱條件概率分布P(Y|X)為條件隨機場。式中w~v表示在圖G=(V,E)中與結點v有邊連接的所有結點w，w ！= v表示結點v以外的所有結點，Yv，Yu與Yw為結點v，u與w對應的隨機變量。

線性鏈條件隨機場：

在CRF的定義中，我們并沒有要求X和Y有相同的結構。而現實中，我們一般都假設X和Y有相同的圖結構，在《統計學習方法》中主要說明的是線性鏈的情況，如圖有：

 

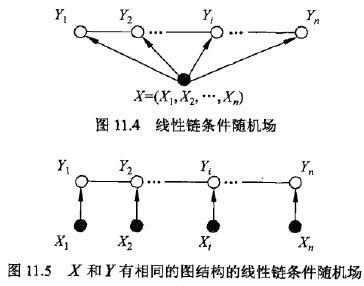
即: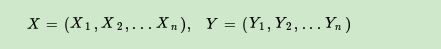

X和Y有相同的結構的CRF就構成了線性鏈條件隨機場(Linear chain Conditional Random Fields,以下簡稱 linear-CRF)。

linear-CRF的數學定義：

設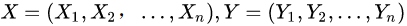

均為線性鏈表示的隨機變量序列，在給定隨機變量序列X的情況下，隨機變量Y的條件概率分布 構成條件隨機場，即滿足馬爾科性：

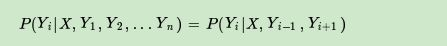
則稱 為線性鏈條件隨機場。

條件隨機場的參數化形式

條件隨機場通過定義特征函數和權重系數來轉換成機器可以學習的模型。

下面先給出公式，然后進行解釋：

 

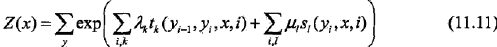
式中，tk和sl是特征函數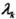，和ul是對應的權值.Z(x)是規范化因子，求和是在所有可能的輸出序列上進行的

上式是線性鏈條件隨機場模型的基本形式，表示給定輸入序列x，對輸出序列y預測的條件概率。tk是定義在邊上的特征函數，稱為轉移特征，依賴于當前和前一個位置，sl是定義在結點上的特征函數，稱為狀態特征，依賴于當前位置。兩者都依賴于位置，是局部特征函數。通常，特征函數tk和sl取值為1或0；當滿足特征條件時取值為1，否則為0。條件隨機場完全由特征函數和對應的權值確定。

線性鏈條件隨機場的簡化形式

即整理特征函數，將其統一起來。

設有K1個轉移特征，K2個狀態特征，K=K1 + K2,，記

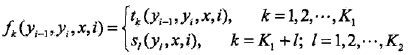
然后，對轉移與狀態特征在各個位置i求和，記作

 

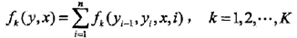
對應的權值為

 

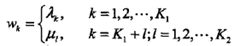
條件隨機場為

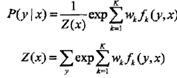
以向量形式表示為

 

 

 

 

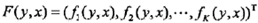
則條件隨機場的向量形式為

 

 

 

 

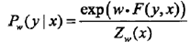
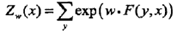
條件隨機場的矩陣形式

引進特殊的起點和終點狀態標記y0 =start , yn+1=stop。對觀測序列x的每一個位置i，定義一個m階矩陣(m是標記yi取值的個數)

 

條件概率為

 

 

 

 

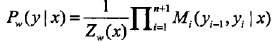
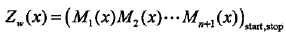
注意，y0 =start , yn+1=stop表示開始狀態與終止狀態，Zw(x)是以start為起點stop為終點通過狀態的所有路徑y1,y2,...,yn的非規范化概率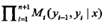之和。

與隱馬爾可夫模型類似，條件隨機場也有三個問題：

1）條件隨機場的概率計算問題

條件隨機場的概率計算問題是給定條件隨機場P(Y|X)，輸入序列x和輸出序列Y，計算條件概率P(Yi=yi|x )，P(Yi-1=yi-1,Yi=yi|x)以及相應的數學期望的問題。為了方便起見，引進了前向-后向算法。

對每個指標i = 0,1,...,n + 1，定義前向向量

 

 

 

 

 

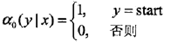
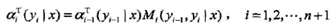
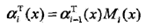
ai(yi | x)表示在位置i的標記是yi并且到位置i的前部分標記序列的非規范化概率，yi可取的值有m個，所以ai是m維列向量。

定義后向向量

 

 

 

 

 

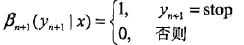
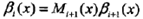
表示在位置i的標記是yi并且從i+1到n的后部分標記序列的非規范化概率。

可以得到

 

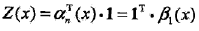
按照前向-后向向量的定義，很容易計算標記序列在位置i是標記yi的條件概率和在位置i-1與i是標記yi-1和yi的條件概率：

有了上一節計算的條件概率，我們也可以很方便的計算聯合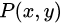分布和條件分布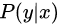的期望。（注：期望是每次的概率乘以其結果的總和）

期望值的計算

根據上面我們求得的條件概率，可以很方便地算出聯合分布P(x,y)和條件分布P(y|x)的期望。

 

前向后向算法總結：

從上面可以看出非規范化概率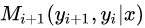與HMM的隱藏狀態轉移概率的作用類似，只是非規范化不要求所有的狀態的概率和為1，HMM的隱藏狀態轉移概率是規范化的，可以看出，線性鏈條件隨機場更靈活一些。

條件隨機場的學習算法

條件隨機場模型實際上是定義在時序數據上的對數線形模型，其學習方法包括極大似然估計和正則化的極大似然估計。具體的優化實現算法有改進的迭代尺度法IIS、梯度下降法以及擬牛頓法。

參數學習算法與最大熵模型算法沒什么區別，條件隨機場模型的訓練數據的對數似然函數為：

 

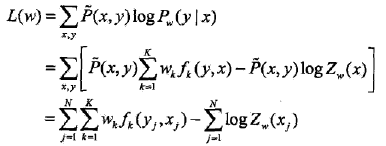
關于轉移特征的更新方程為

 

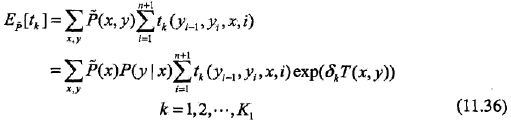
關于狀態特征的更新方程為

 

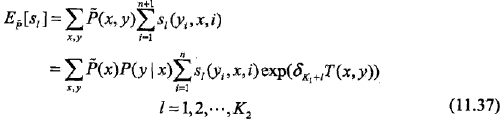
T(x,y)是在數據(x,y)中出現所有特征數的總和:

 

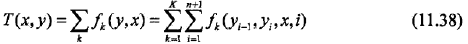
具體算法如下：

 

擬牛頓法：

對于條件隨機場模型，學習的優化目標函數是：

 

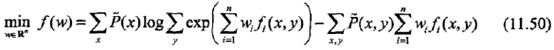
其梯度函數是

 

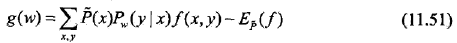
條件隨機場的預測算法：

預測算法也是采用了維特比算法，不需要重新推導，詳情請見之前的HMM的預測算法，里面有相關算法和實例，相信解釋的比較清楚。