隱馬爾可夫模型
本文主要參考了《統(tǒng)計(jì)學(xué)習(xí)方法》及https://github.com/aespresso/a_journey_into_math_of_ml
請(qǐng)各位大佬多多指正。
隱馬爾可夫模型(hidden Markov model, HMM)描述由隱藏的馬爾可夫鏈隨機(jī)生成觀測(cè)序列的過(guò)程,屬于生成模型。可用于自動(dòng)分詞、詞性標(biāo)注、命名實(shí)體識(shí)別等。
以命名實(shí)體識(shí)別為例:
一段文本:武漢市成立自由貿(mào)易試驗(yàn)區(qū)。我們需要識(shí)別出濟(jì)南市(地點(diǎn)), 自由貿(mào)易試驗(yàn)區(qū)(地點(diǎn)).
在我們今天使用的NER數(shù)據(jù)集中, 一共有7個(gè)標(biāo)簽:
- "B-ORG": 組織或公司(organization)
- "I-ORG": 組織或公司
- "B-PER": 人名(person)
- "I-PER": 人名
- "O": 其他非實(shí)體(other)
- "B-LOC": 地名(location)
- "I-LOC": 地名
文本中以每個(gè)字為單位,每個(gè)字都對(duì)應(yīng)一個(gè)標(biāo)簽。注意:實(shí)體開(kāi)頭的那個(gè)字使用開(kāi)頭為‘B’的標(biāo)簽來(lái)標(biāo)注,實(shí)體中間或結(jié)尾的部分用‘I’來(lái)標(biāo)注。
舉個(gè)栗子:自(B-LOC)貿(mào)(I-LOC)區(qū)(I-LOC)
什么是隱馬爾科夫模型?
隱馬爾可夫模型是關(guān)于時(shí)序的概率模型,描述了一個(gè)由隱藏的馬爾可夫鏈隨機(jī)生成不可觀測(cè)的狀態(tài)隨機(jī)序列,再由各個(gè)狀態(tài)生成一個(gè)觀測(cè)而產(chǎn)生觀測(cè)隨機(jī)序列的過(guò)程,如下圖所示:
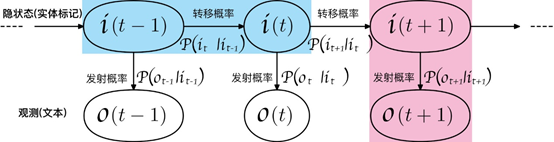
在上述的命名實(shí)體識(shí)別的例子中,隱狀態(tài)序列是實(shí)體標(biāo)記序列, 而可觀測(cè)序列是我們可讀的原始語(yǔ)料文本序列。
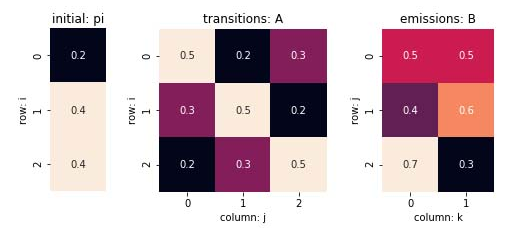
隱馬爾可夫模型由初始狀態(tài)概率向量pi、狀態(tài)轉(zhuǎn)移概率矩陣A(對(duì)應(yīng)上圖的轉(zhuǎn)移概率)和觀測(cè)概率矩陣B(對(duì)應(yīng)上圖的發(fā)射概率)決定。A,B,pi稱為隱馬爾可夫模型的三要素,可表示為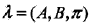
設(shè)可觀測(cè)狀態(tài)序列是所有漢字的集合,用V表示,已知字?jǐn)?shù)為M;設(shè)所有可能的隱藏狀態(tài)集合為Q,一共有N種隱藏狀態(tài)。
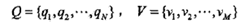
I是長(zhǎng)度為T(mén)的狀態(tài)序列,O是對(duì)應(yīng)的觀測(cè)序列。注:每個(gè)狀態(tài)序列都對(duì)應(yīng)一個(gè)觀測(cè)序列。
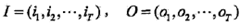
A是狀態(tài)轉(zhuǎn)移概率矩陣:
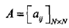

是在時(shí)刻t處于狀態(tài)qi的條件下在時(shí)刻t+1轉(zhuǎn)移到狀態(tài)qj的概率。
B是觀測(cè)概率矩陣:
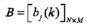
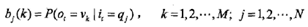
是在時(shí)刻t處于狀態(tài)qj的條件下生成觀測(cè)vk的概率。
n是初始狀態(tài)概率向量:
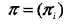
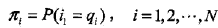
是時(shí)刻t=1處于狀態(tài)qi的概率。
由定義可知,隱馬爾可夫模型作了兩個(gè)基本假設(shè):
(1) 齊次馬爾可夫性假設(shè),即假設(shè)隱藏的馬爾可夫鏈在任意時(shí)刻t的狀態(tài)只依賴于其前一時(shí)刻的狀態(tài),與其他時(shí)刻的狀態(tài)及觀測(cè)無(wú)關(guān),也與時(shí)刻t無(wú)關(guān)
(2) 觀測(cè)獨(dú)立性假設(shè),即假設(shè)任意時(shí)刻的觀測(cè)只依賴于該時(shí)刻的馬爾可夫鏈的狀態(tài),與其他觀測(cè)及狀態(tài)無(wú)關(guān).
一般而言,隱馬爾可夫模型有3個(gè)基本問(wèn)題
(1)概率計(jì)算問(wèn)題。給定模型λ和觀測(cè)序列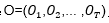 ,計(jì)算在模型之下觀測(cè)序列O出現(xiàn)的概率。
,計(jì)算在模型之下觀測(cè)序列O出現(xiàn)的概率。
(2)學(xué)習(xí)問(wèn)題。己知觀測(cè)序列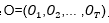 ,估計(jì)模型參數(shù),使得在該模型下觀測(cè)序列概率最大。即用極大似然估計(jì)的方法估計(jì)參數(shù)。
,估計(jì)模型參數(shù),使得在該模型下觀測(cè)序列概率最大。即用極大似然估計(jì)的方法估計(jì)參數(shù)。
(3)預(yù)測(cè)問(wèn)題,也稱為解碼問(wèn)題。己知模型和觀測(cè)序列 ,求對(duì)給定觀測(cè)序列條件概率P(I | O)最大的狀態(tài)序列
,求對(duì)給定觀測(cè)序列條件概率P(I | O)最大的狀態(tài)序列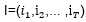 ,即給定觀測(cè)序列,求最有可能的對(duì)應(yīng)的狀態(tài)序列。注:我們常說(shuō)的詞性標(biāo)注、命名實(shí)體識(shí)別就是此類。
,即給定觀測(cè)序列,求最有可能的對(duì)應(yīng)的狀態(tài)序列。注:我們常說(shuō)的詞性標(biāo)注、命名實(shí)體識(shí)別就是此類。
(1)概率計(jì)算問(wèn)題:
1)直接計(jì)算法:
計(jì)算量太大,一般不考慮
2)前向算法:
給定隱馬爾可夫模型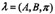 ,定義到時(shí)刻t部分觀測(cè)序列o1,o2,... ,ot 且狀態(tài)為qi的概率為前向概率,記作
,定義到時(shí)刻t部分觀測(cè)序列o1,o2,... ,ot 且狀態(tài)為qi的概率為前向概率,記作
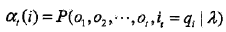
可以遞推地求得前向概率及觀測(cè)序列概率

步驟(1)初始化前向概率,是初始時(shí)刻的狀態(tài)i1=qi和觀測(cè)o1的聯(lián)合概率。
步驟(2)是前向概率的遞推公式,應(yīng)該是對(duì)t時(shí)刻進(jìn)行遞推算出直到t=T-1時(shí)刻的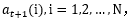 t=1,2,…,T-1。
t=1,2,…,T-1。
計(jì)算到時(shí)刻t+1部分觀測(cè)序列為o1,o2,... ,ot ,ot+1且在時(shí)刻t+1處于狀態(tài)qi的前向概率。(j)是到時(shí)刻t觀測(cè)到o1,o2,... ,ot并在時(shí)刻t處于狀態(tài)的前向概率,那么乘積(j)就是到時(shí)刻t觀測(cè)到o1,o2,... ,ot在在時(shí)刻t處于狀態(tài)而在時(shí)刻t+1到達(dá)狀態(tài)qi的聯(lián)合概率。對(duì)這個(gè)乘積在時(shí)刻t的所有可能的N個(gè)狀態(tài)求和,其結(jié)果就是到時(shí)刻t觀測(cè)為o1,o2,... ,ot并在時(shí)刻t+1處于狀態(tài)qi的聯(lián)合概率。方括弧里的值與觀測(cè)概率bi(ot+1)的乘積恰好是到時(shí)刻t+1觀測(cè)到o1,o2,... ,ot ,ot+1且在時(shí)刻t+1處于狀態(tài)qi的前向概率。即對(duì)t時(shí)刻進(jìn)行遞推算出t=T-1時(shí)刻的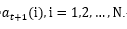
步驟(3):終止 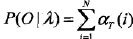
減少計(jì)算量的原因在于每一次計(jì)算直接引用前一個(gè)時(shí)刻的計(jì)算結(jié)果,避免重復(fù)計(jì)算。利用前向概率計(jì)算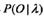 的計(jì)算量是O(N^2·T)階的,而不是直接計(jì)算的O(T·N^2)階。
的計(jì)算量是O(N^2·T)階的,而不是直接計(jì)算的O(T·N^2)階。
(3)后向算法
給定隱馬爾可夫模型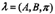 ,定義在時(shí)刻t狀態(tài)為qi的條件下,從t+1到T的部分觀測(cè)序列為ot+1,ot+2 ,... ,oT的概率為后向概率,記作
,定義在時(shí)刻t狀態(tài)為qi的條件下,從t+1到T的部分觀測(cè)序列為ot+1,ot+2 ,... ,oT的概率為后向概率,記作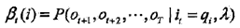
可以遞推地求得后向概率及觀測(cè)序列概率

步驟(1)初始化后向概率,對(duì)最終時(shí)刻的所有狀態(tài)qi規(guī)定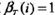
步驟(2)是后向概率的遞推公式,應(yīng)該是對(duì)t時(shí)刻進(jìn)行遞推算出直到t=1時(shí)刻的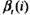 ,i=1,2,...,N,t= T-1,T-2,…,1。
,i=1,2,...,N,t= T-1,T-2,…,1。
為了計(jì)算在時(shí)刻t狀態(tài)為qi的條件下,從t+1到T的部分觀測(cè)序列為, ,... ,的后向概率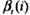 。只需考慮在時(shí)刻t十1所有可能的N個(gè)狀態(tài)
。只需考慮在時(shí)刻t十1所有可能的N個(gè)狀態(tài)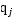
的轉(zhuǎn)移概率(即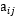 項(xiàng)),以及在此狀態(tài)下的觀測(cè)
項(xiàng)),以及在此狀態(tài)下的觀測(cè)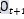 的觀測(cè)概率(即bj(oi+1)項(xiàng)),然后考慮狀態(tài)qj之后的觀測(cè)序列的后向概率(即
的觀測(cè)概率(即bj(oi+1)項(xiàng)),然后考慮狀態(tài)qj之后的觀測(cè)序列的后向概率(即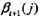 項(xiàng))。
項(xiàng))。
步驟(3)求解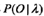 的思路與步驟(2)一致,只是初始概率
的思路與步驟(2)一致,只是初始概率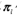 代替轉(zhuǎn)移概率.
代替轉(zhuǎn)移概率.
(2)學(xué)習(xí)問(wèn)題
監(jiān)督學(xué)習(xí)方法:
采根據(jù)已給數(shù)據(jù),采用極大似然估計(jì)法來(lái)估計(jì)隱馬爾科夫模型的參數(shù)
1、轉(zhuǎn)移概率的估計(jì)
設(shè)樣本中時(shí)t處于狀態(tài)i時(shí)刻t+1轉(zhuǎn)移到狀態(tài)j的頻數(shù)為Aij,那么狀態(tài)轉(zhuǎn)移概率的估計(jì)是

2、觀測(cè)概率bj(k)的估計(jì)
設(shè)樣本中狀態(tài)為j并觀測(cè)為k的頻數(shù)是Bjk,那么狀態(tài)為j觀測(cè)為k的概率的估計(jì)是
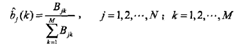
3、初始狀態(tài)概率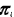 的估計(jì)為S個(gè)樣本中初始狀態(tài)為qi的頻率
的估計(jì)為S個(gè)樣本中初始狀態(tài)為qi的頻率
(3)預(yù)測(cè)算法
這里主要介紹維特比算法。維特比算法實(shí)際是用動(dòng)態(tài)規(guī)劃解隱馬爾可夫模型預(yù)側(cè)問(wèn)題,即用動(dòng)態(tài)規(guī)劃找到概率最大路徑(最優(yōu)路徑)。在命名實(shí)體識(shí)別種。就是通過(guò)維特比算法找到文本對(duì)應(yīng)的最可能的實(shí)體標(biāo)注序列。
總結(jié):計(jì)算并記錄在每個(gè)時(shí)刻中每種隱狀態(tài)的最大概率,還記錄最大概率是從前一時(shí)刻的哪種隱狀態(tài)轉(zhuǎn)移的,最后從結(jié)尾依次回溯最大概率,即得到了最優(yōu)路徑。
先尊重下公式算法,然后舉實(shí)例說(shuō)明:

為了更好理解,下面舉實(shí)例說(shuō)明:
假設(shè)有2種可能觀測(cè)的結(jié)果{0,1},有3種可能的隱狀態(tài)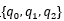 ,我們已經(jīng)觀測(cè)到一種序列O=
,我們已經(jīng)觀測(cè)到一種序列O=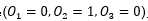 ,
,
并已經(jīng)學(xué)習(xí)到了如下圖所示的隱馬模型的參數(shù)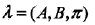
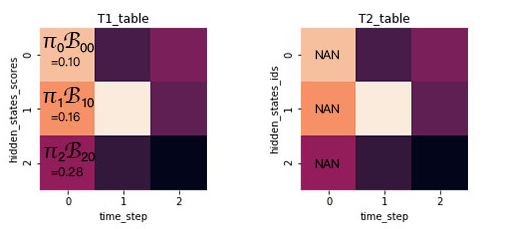
接著我們建立兩張表分別來(lái)存儲(chǔ)之前提到的每種隱狀態(tài)的最大概率和最大概率是從前一時(shí)刻的哪種隱狀態(tài)轉(zhuǎn)移的,如圖有:
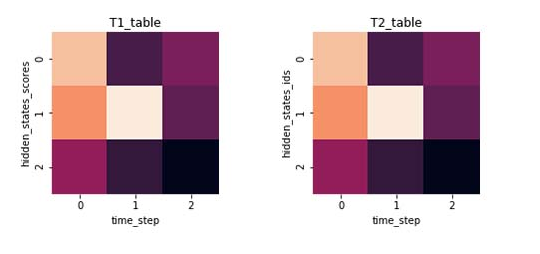
1、t=0時(shí)刻是初始狀態(tài),這時(shí)根據(jù)初始隱狀態(tài)π和t=1時(shí)的觀測(cè)結(jié)果= 0,計(jì)算T1在t=0時(shí)的隱狀態(tài),T1[0][0]= π0·B[0][0]=0.2·0.5=0.1,T1[1][0]= π1·B[1][0]=0.4·0.4=0.16,T1[0][3]= π2·B[0][2]=0.4·0.7=0.28,因?yàn)榇藭r(shí)是初始狀態(tài),故t=0時(shí)刻T2都為空,則得到下表:
現(xiàn)在計(jì)算t=1時(shí)刻的情況,以計(jì)算T1[0][1]舉例,從t=0到t=1有三種可能性,分別是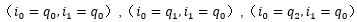 ,
,
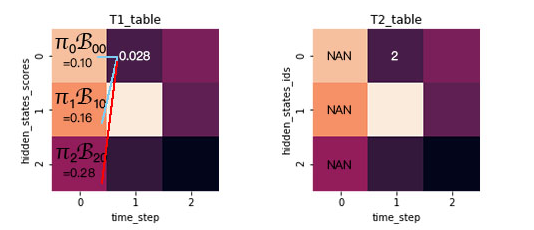
取三種路徑中可能性最大的那條路徑,T1[0][1]=max{0.1·0.5·0.5,0.16·0.3·0.5,0.28·0.2·0.5}=0.028,再記錄當(dāng)前最大概率前一時(shí)刻的的隱狀態(tài)I,
則T2[0][1]=argmax{0.1·0.5·0.5,0.16·0.3·0.5,0.28·0.2·0.5}=2,如下圖所示:
接下來(lái)的步驟同上,最后得到下表:
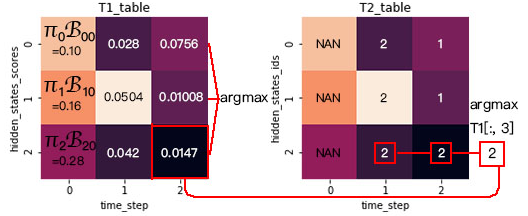
回溯計(jì)算:
計(jì)算最后一步最大可能的隱狀態(tài),即求T1在t=2時(shí)的argmax:
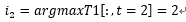
由T2進(jìn)行回溯,因?yàn)橹熬痛鎯?chǔ)了當(dāng)前最大概率是從前一步轉(zhuǎn)移過(guò)來(lái)的隱狀態(tài):
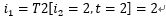
同樣方法得到:
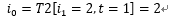
那么就得到了最大可能的隱狀態(tài)序列:

時(shí)間復(fù)雜度: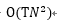



 浙公網(wǎng)安備 33010602011771號(hào)
浙公網(wǎng)安備 33010602011771號(hào)