引理：等腰梯形的四個頂點(diǎn)共圓。

易證。

牛頓定理三：四邊形 \(A_1 A_2 A_3 A_4\) 與其內(nèi)切圓的四個切點(diǎn)分別為 \(B_1,B_2,B_3,B_4\)，證明：\(A_1 A_3,A_2 A_4,B_1 B_3,B_2 B_4\) 四線共點(diǎn)。

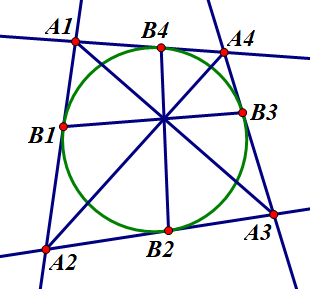
證明：在直線 \(A_1 A_2\) 上取兩個點(diǎn) \(P_1,P_2\)，在直線 \(A_2 A_3\) 上取兩個點(diǎn) \(P_3,P_4\)，在直線 \(A_3 A_4\) 上取兩個點(diǎn) \(P_5,P_6\)，在直線 \(A_4 A_1\) 上取兩個點(diǎn) \(P_7,P_8\)，使得：

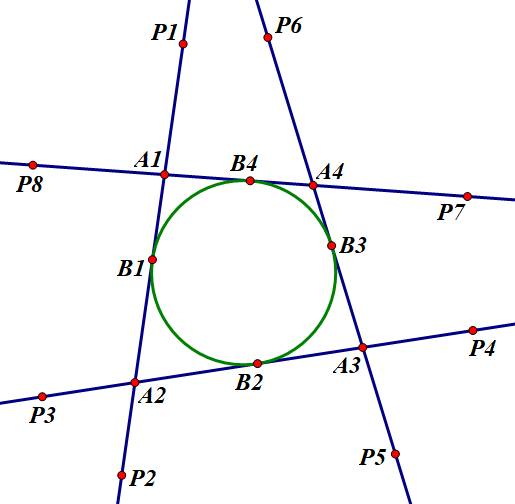
由平行線分線段成比例的逆定理，得：

故有四個等腰梯形：\(P_1 P_6 B_3 B_1,B_1 B_3 P_5 P_2,P_7 P_4 B_2 B_4,B_4 B_2 P_3 P_8\)。由引理，這些等腰梯形的四個頂點(diǎn)共圓。

考察圓 \(P_1 P_6 B_3 B_1\) 與圓 \(P_7 P_4 B_2 B_4\)，簡記為圓 \(\alpha\) 與圓 \(\beta\)：

其中圓 \(\alpha\) 與原內(nèi)切圓的根軸為 \(B_1 B_3\)，圓 \(\beta\) 與原內(nèi)切圓的根軸為 \(B_4 B_2\)。

由切線長定理與 \(B_1 P_1=B_2 P_4\)，可得 \(A_2\) 關(guān)于圓 \(\alpha\) 的冪 \(A_2 B_1 \cdot A_2 P_1\) 等于 \(A_2\) 關(guān)于圓 \(\beta\) 的冪 \(A_2 B_2 \cdot A_2 P_4\)。故 \(A_2\) 在圓 \(\alpha\) 與圓 \(\beta\) 的根軸上。

同理可得 \(A_4\) 也在圓 \(\alpha\) 與圓 \(\beta\) 的根軸上。所以 \(A_2 A_4\) 即為圓 \(\alpha\) 與圓 \(\beta\) 的根軸。

由根心定理，圓 \(\alpha\)、圓 \(\beta\)、原內(nèi)切圓的三條根軸 \(B_1 B_3,B_4 B_2,A_2 A_4\) 共點(diǎn)。

同理考察圓 \(\alpha\) 與圓 \(B_4 B_2 P_3 P_8\)，可得 \(B_1 B_3,B_4 B_2,A_1 A_3\) 共點(diǎn)。

故 \(A_1 A_3,A_2 A_4,B_1 B_3,B_2 B_4\) 四線共點(diǎn)。證畢。