一般的尺規作圖要求「圓規不能固定」，即圓規的唯一作用是：以任一點為圓心，以任意距離為半徑作圓。而初中數學中的「作一條線段等于已知線段」的作法中涉及圓規的「截取與平移」，這是不允許的。

本文介紹在一般的尺規作圖中「截取已知線段」的三種方法。

問題：已知平面上一線段 \(AB\) 和一點 \(C\)，求作一點 \(D\) 使得 \(CD=AB\)。

方法一：通過等邊三角形構造三角形全等。

關鍵方法：已知平面上一線段 \(AB\)，求作等邊三角形 \(ABP\)：
以 \(A\) 為圓心，\(AB\) 為半徑作圓。以 \(B\) 為圓心，\(AB\) 為半徑作圓。兩圓交點即為 \(P\)（不妨取上方的交點）。

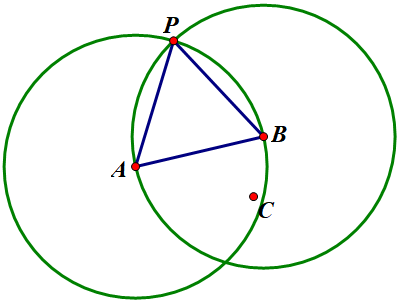
對于原問題，同上方法作等邊三角形 \(ACQ\)：

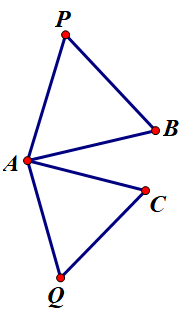
同上方法作等邊三角形 \(PQD\) 即為所求。

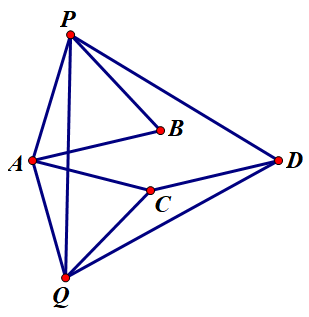
方法二（《幾何原本》第一卷，命題 \(\text{I.2}\)）：

作等邊三角形 \(BCP\)：

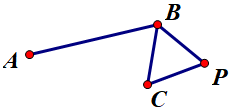
作射線 \(PB,PC\)。以 \(B\) 為圓心，\(AB\) 為半徑作圓。交射線 \(PB\) 于 \(Q\)：

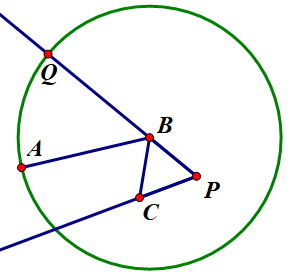
以 \(P\) 為圓心，\(PQ\) 為半徑作圓。交射線 \(PC\) 即為 \(D\)。

方法三：通過中垂線構造線段相等。

以 \(A\) 為圓心，\(AC\) 為半徑作圓。以 \(C\) 為圓心，\(AC\) 為半徑作圓。兩圓交于 \(P,Q\)，作直線 \(PQ\)：

以 \(A\) 為圓心，\(AB\) 為半徑作圓。交直線 \(PQ\) 即為 \(D\)。