高速艇在波浪中的垂直運動MATLAB模擬與仿真
1.程序功能描述
高速艇在波浪中的垂直運動MATLAB模擬與仿真。參考文獻《Dynamic motions of planing vessels in head seas》中的方法,對滑航船在規則海頭海中的動態響應進行了數值研究。采用二維 邊界元方法來解決2D橫截面中的初始邊界值問題,其中滿足非線性自由表面條件和精確的體邊界條件。
2.測試軟件版本以及運行結果展示
MATLAB2022A版本運行
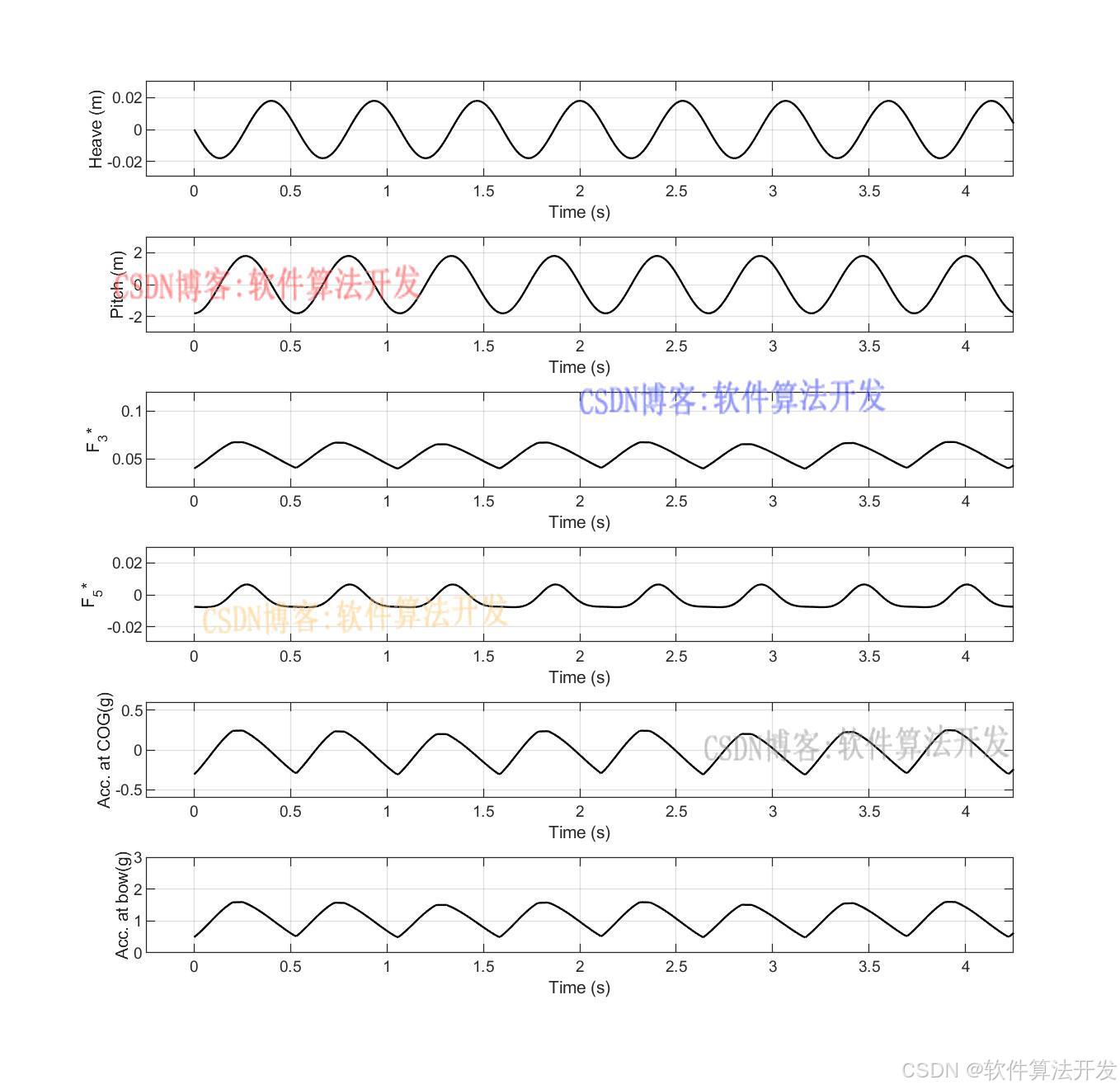
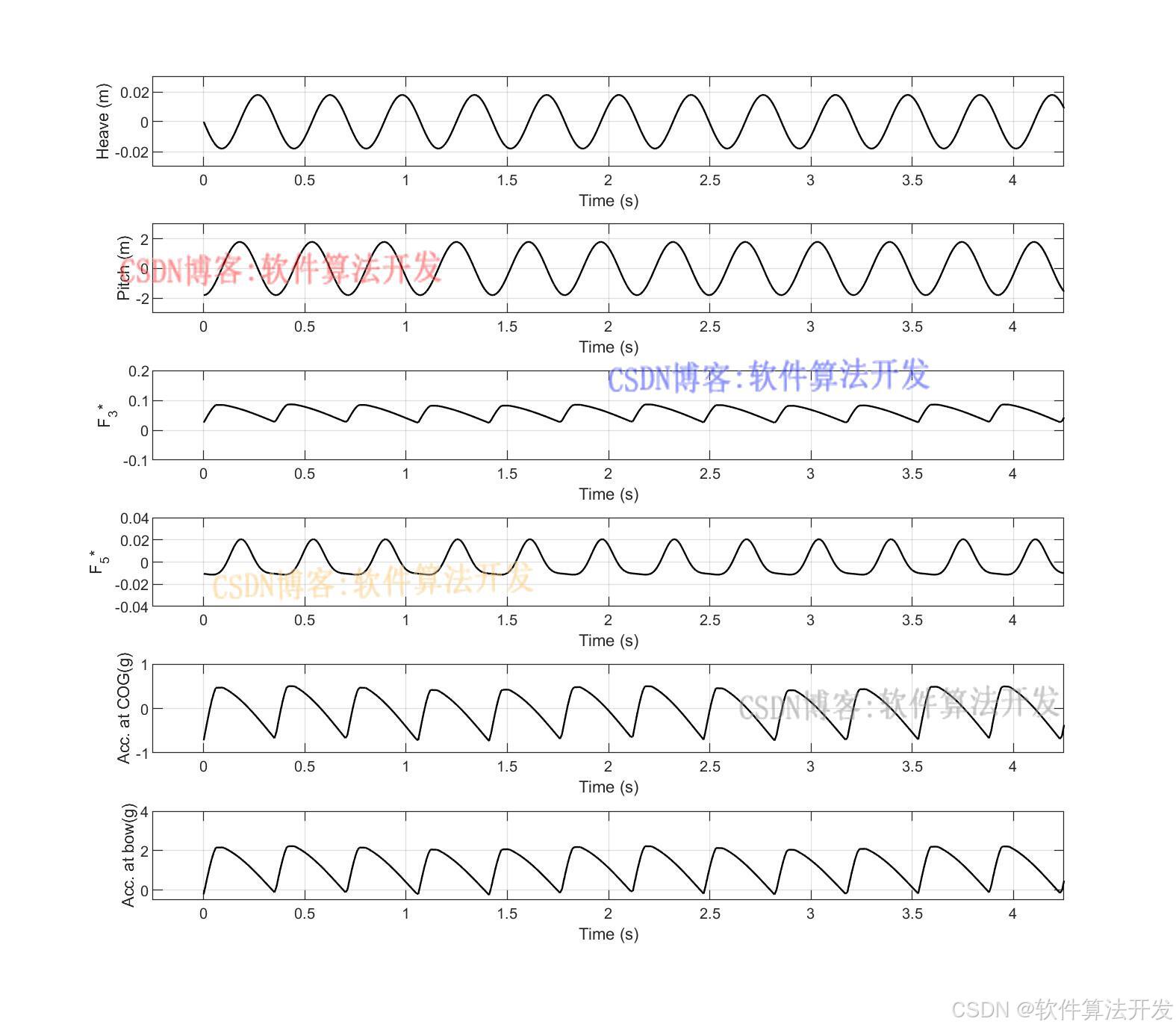
3.核心程序
................................................... %accelerations1 Fz = -DADt.*V - A.*DVDt + p*g*S;%(27) Fz0 = mean(Fz); Acc1 = (Fz-Fz0)/M; %accelerations2 Acc2 = Acc1+fxt/M; figure; subplot(611); plot(x,r3,'k','linewidth',1); xlabel('Time (s)'); ylabel('Heave (m)'); xlim([-0.25,4.25]); ylim([-0.03,0.03]); grid on subplot(612); plot(x,r5,'k','linewidth',1); xlabel('Time (s)'); ylabel('Pitch (m)'); xlim([-0.25,4.25]); ylim([-3,3]); grid on subplot(613); plot(x,fxt,'k','linewidth',1); xlabel('Time (s)'); ylabel('F_3*'); xlim([-0.25,4.25]); ylim([0.02,0.12]); grid on subplot(614); plot(x,F5,'k','linewidth',1); xlabel('Time (s)'); ylabel('F_5*'); xlim([-0.25,4.25]); ylim([-0.03,0.03]); grid on subplot(615); plot(x,Acc1,'k','linewidth',1); xlabel('Time (s)'); ylabel('Acc. at COG(g)'); xlim([-0.25,4.25]); ylim([-0.6,0.6]); grid on subplot(616); plot(x,Acc2,'k','linewidth',1); xlabel('Time (s)'); ylabel('Acc. at bow(g)'); xlim([-0.25,4.25]); ylim([0,3]); grid on 16_065m
4.本算法原理
滑行艇在休閑、體育和軍事領域應用廣泛,其在波浪中的運動問題復雜。早期研究多關注穩態問題,對非穩態問題研究不足。2D + t 理論可用于解決強非線性水動力問題,本研究基于此理論改進并應用于滑行艇在波浪中的動態運動模擬。
定義坐標系,假定水為無黏性、不可壓縮且水流無旋,引入速度勢描述水流,將總速度勢分解為入射波勢和擾動勢。在船體表面、自由表面等邊界上給出相應條件,得到擾動速度勢的時變邊值問題。考慮船舶在波浪中的非穩態運動,僅研究垂蕩和縱搖運動,給出船體表面點的速度表達式。
基于細長體假設簡化三維問題為二維時變問題,得到二維拉普拉斯方程和邊界條件。使用邊界元法求解二維問題,考慮水流分離和壓力計算,引入輔助函數求解。在數值計算中,先進行穩態計算得到初始條件,再逐步引入入射波。通過在多個垂直固定橫剖面求解邊值問題,計算船體的總垂直力和縱搖力矩,進而求解運動方程得到垂蕩和縱搖運動。在新平面計算時要考慮船舶截面的淹沒情況,并采用修正的初始自由表面輪廓。利用近似方法計算船體前部的力分布,逐步引入波浪效應。建立以船舶重心為原點的慣性坐標系下的垂蕩和縱搖運動方程,考慮附加質量力對運動方程進行改寫,以提高計算精度。在某些情況下需替換特定附加質量系數以保證計算收斂。
Fridsma 進行了滑行艇在波浪中的模型試驗,本文對其中四個配置進行數值研究,這些配置代表不同速度和負載系數。試驗中模型船的一些參數已知,試驗考慮了不同波長的規則入射波,但數值研究未考慮船頭特殊形狀。
先對每個配置進行穩態滑行模擬得到初始條件,再求解二維邊值問題得到船舶運動響應。通過收斂性測試確定合適的計算平面數量。分析不同配置下船舶運動響應的時間歷程,發現速度較快的情況過渡階段更長,非線性在接近共振頻率時更顯著。對比數值結果和實驗結果,研究三維修正對結果的影響,發現三維修正使結果更接近實驗值,對縱搖運動影響更大,對艏部峰值加速度影響顯著,同時指出計算與實驗差異的誤差來源。
2D + t 理論可用于研究滑行艇在迎浪中的動態垂直運動,數值結果與實驗有較好一致性。發現非線性在接近共振頻率時更強,高弗勞德數下共振波長更大,艉部三維效應是重要誤差源。未來應進一步研究艉部三維效應及其他三維效應,將理論推廣到非棱柱形滑行船體和高速半排水船。
5.完整程序
VVV


