基于UKF-IMM無跡卡爾曼濾波與交互式多模型的軌跡跟蹤算法matlab仿真,對比EKF-IMM和UKF
1.程序功能描述
基于UKF-IMM無跡卡爾曼濾波與交互式多模型的軌跡跟蹤算法matlab仿真,對比EKF-IMM和UKF。
2.測試軟件版本以及運行結果展示
MATLAB2022A版本運行


3.核心程序
.............................................................................
% 繪制目標運動與傳感器分布的圖形,展示 IMM - UKF 算法的跟蹤效果
%目標運動與傳感器分布
figure
% 繪制目標的真實軌跡
plot(TargetState(1,:),TargetState(4,:),'k','LineWidth',2);
hold on
% 循環處理每個節點
for i = 1:NumberNode
% 繪制 IMM - UKF 算法的狀態估計軌跡
plot(Xfstate(1,:),Xfstate(4,:),'-mo',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.5,0.9,0.0]);
hold on
% 繪制真實節點的位置
plot(NodeDistribution(1,i),NodeDistribution(2,i),'bo','LineWidth',1);
hold on
% 在節點位置旁邊標注節點編號
text(NodeDistribution(1,i)+0.5,NodeDistribution(2,i)+0.5,num2str(i));
hold on
% 繪制 IMM - UKF 算法估計的節點位置
plot(pest(1,i),pest(2,i),'rs','LineWidth',1);
hold on
% 添加圖例說明不同線條和標記的含義
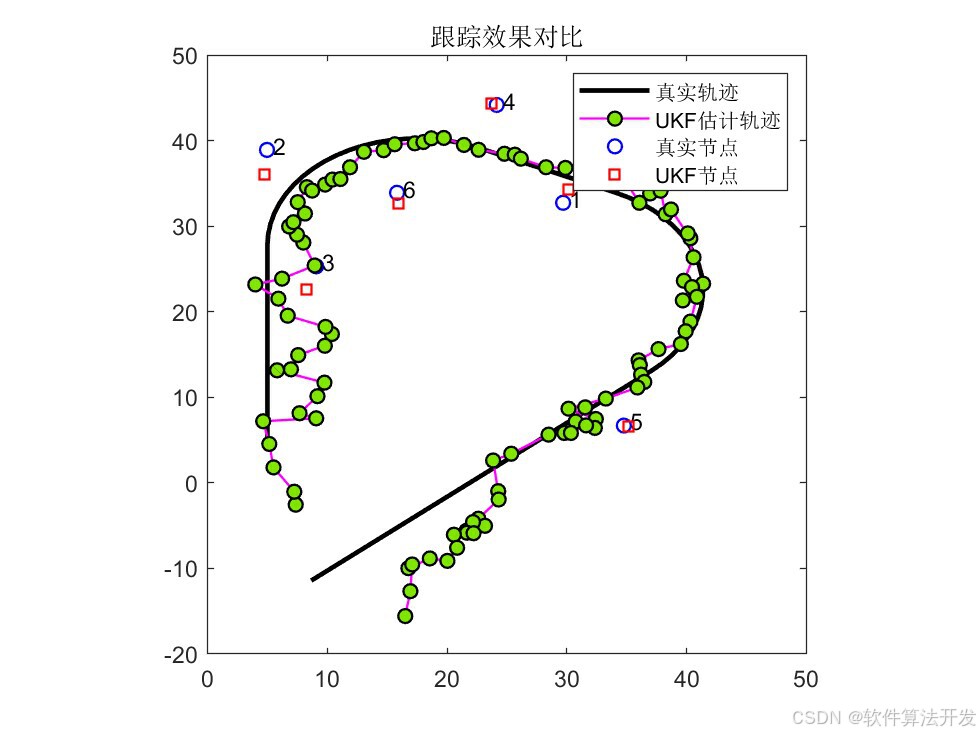
legend('真實軌跡','IMM-UKF估計軌跡','真實節點','IMM-UKF節點');
% 設置圖形標題
title('跟蹤效果對比');
end
% 設置坐標軸為正方形,使圖形比例合適
axis square
% 繪制目標運動與傳感器分布的圖形,展示 IMM - EKF 算法的跟蹤效果
figure
% 繪制目標的真實軌跡
plot(TargetState(1,:),TargetState(4,:),'k','LineWidth',2);
hold on
% 循環處理每個節點
for i = 1:NumberNode
% 繪制 IMM - EKF 算法的狀態估計軌跡
plot(Xfstate2(1,:),Xfstate2(4,:),'-mo',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.5,0.9,0.0]);
hold on
% 繪制真實節點的位置
plot(NodeDistribution(1,i),NodeDistribution(2,i),'bo','LineWidth',1);
hold on
% 在節點位置旁邊標注節點編號
text(NodeDistribution(1,i)+0.5,NodeDistribution(2,i)+0.5,num2str(i));
hold on
% 繪制 IMM - EKF 算法估計的節點位置
plot(pest2(1,i),pest2(2,i),'rs','LineWidth',1);
hold on
% 添加圖例說明不同線條和標記的含義
legend('真實軌跡','IMM-EKF估計軌跡','真實節點','IMM-EKF節點');
% 設置圖形標題
title('跟蹤效果對比');
end
% 設置坐標軸為正方形,使圖形比例合適
axis square
% 繪制目標運動與傳感器分布的圖形,展示 UKF 算法的跟蹤效果
figure
% 繪制目標的真實軌跡
plot(TargetState(1,:),TargetState(4,:),'k','LineWidth',2);
hold on
% 循環處理每個節點
for i = 1:NumberNode
% 繪制 UKF 算法的狀態估計軌跡
plot(Para_sensor3(1,:),Para_sensor3(4,:),'-mo',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.5,0.9,0.0]);
hold on
% 繪制真實節點的位置
plot(NodeDistribution(1,i),NodeDistribution(2,i),'bo','LineWidth',1);
hold on
% 在節點位置旁邊標注節點編號
text(NodeDistribution(1,i)+0.5,NodeDistribution(2,i)+0.5,num2str(i));
hold on
% 繪制 UKF 算法估計的節點位置
plot(pest3(1,i),pest3(2,i),'rs','LineWidth',1);
hold on
% 添加圖例說明不同線條和標記的含義
legend('真實軌跡','UKF估計軌跡','真實節點','UKF節點');
% 設置圖形標題
title('跟蹤效果對比');
end
% 設置坐標軸為正方形,使圖形比例合適
axis square
% 繪制不同算法的誤差隨時間變化的曲線
figure
% 繪制 IMM - UKF 算法的誤差曲線
plot(tms,err1(1,:),'-bs',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.0,0.0]);
hold on;
% 繪制 IMM - EKF 算法的誤差曲線
plot(tms,err2(1,:),'-mo',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.5,0.9,0.0]);
hold on;
% 繪制 UKF 算法的誤差曲線
plot(tms,err3(1,:),'-r>',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.9,0.0]);
hold on;
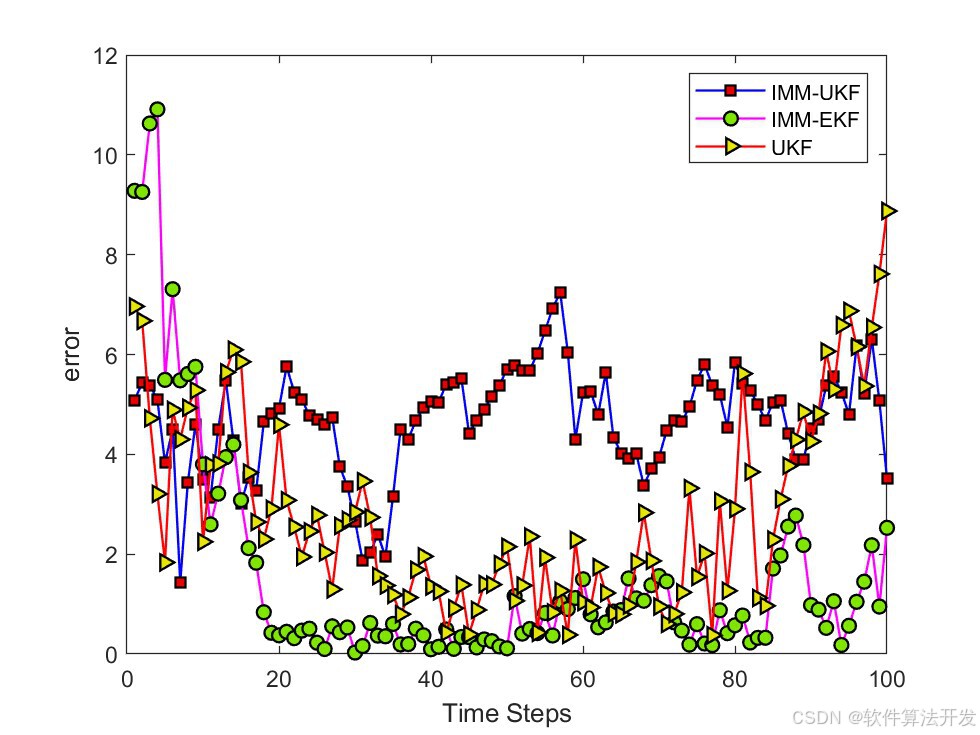
% 添加圖例,說明不同曲線對應的算法
legend('IMM - UKF ','IMM - EKF','UKF');
% 設置 x 軸標簽為時間步
xlabel('Time Steps')
% 設置 y 軸標簽為誤差
ylabel('error')
% 繪制不同算法的平均誤差柱狀圖
figure
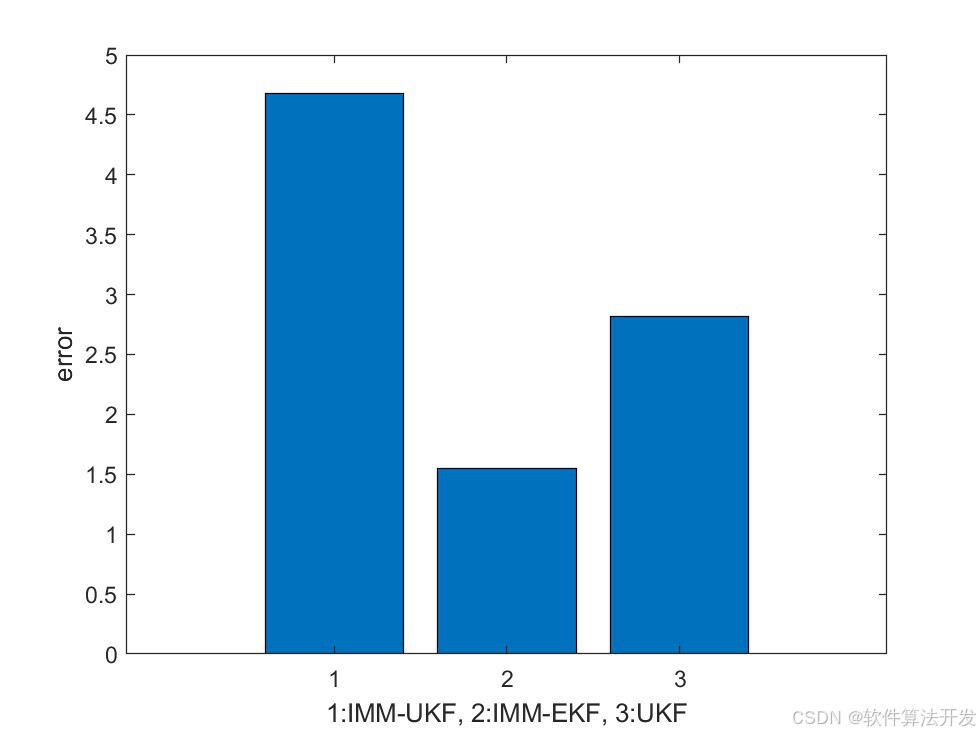
% 繪制三個算法的平均誤差柱狀圖
bar([mean(err1(1,:)),mean(err2(1,:)),mean(err3(1,:))]);
% 設置 x 軸標簽,說明每個柱子對應的算法
xlabel(['1:IMM - UKF, 2:IMM - EKF, 3:UKF']);
% 設置 y 軸標簽為誤差
ylabel('error')
93
4.本算法原理
在許多工程實踐中,往往不能直接得到所需要的狀態變量的真實值。例如雷達在探測目標時,可以通過回波信號等計算出目標的距離、速度和角度等信息。但雷達探測過程中會存在干擾(系統噪聲、地雜波和非目標信號等)的問題,這些干擾會導致回波信號中夾雜有隨機噪聲。我們要在有隨機噪聲的回波信號中分離目標的運動狀態量,準確的得到這個狀態量往往是不可能的,只能根據觀測信號估計這些狀態變量。卡爾曼濾波就是這種通過估計或預測降低噪聲影響的一種好的方法。特別是在線性系統中,卡爾曼濾波是最優的濾波算法。
在軌跡跟蹤問題中,系統狀態通常隨時間變化,并且受到過程噪聲的影響;同時,對系統狀態的觀測也包含觀測噪聲。我們的目標是根據一系列的觀測值來估計系統的真實狀態。UKF 是一種用于非線性系統狀態估計的濾波算法。與傳統的擴展卡爾曼濾波(EKF)不同,UKF 不依賴于對非線性函數的線性化,而是通過一組確定性采樣點(Sigma 點)來近似狀態的概率分布,從而更準確地處理非線性問題。
在kalman濾波算法中用到了狀態轉移方程和量測方程,被估計量隨著時間的變化,呈現的是一個動態估計。在目標跟蹤中,不需要知道目標的運動模型就能實時的修正目標的狀態變量(速度、距離等),具有良好的適應性。但是當目標實施機動變化(突然加、減速或急轉彎等),僅僅采用基本的kalman濾波算法往往得不到理想的結果。這時就需要采用自適應算法。交互多模型(IMM)就應用而生。
目標交互多模型kalman濾波算法在機動目標跟蹤領域得到廣泛應用。IMM算法使用兩個或者多個模型來描述工作過程中可能出現的狀態,最后通過有效的加權融合進行系統狀態估計,很好的克服了單個模型估計誤差較大的問題。
IMM 算法用于處理系統在不同模式下運行的情況。它假設系統存在多個可能的運行模式,每個模式對應一個不同的狀態模型,通過在這些模型之間進行交互和切換,以適應系統模式的變化,從而提高狀態估計的準確性。

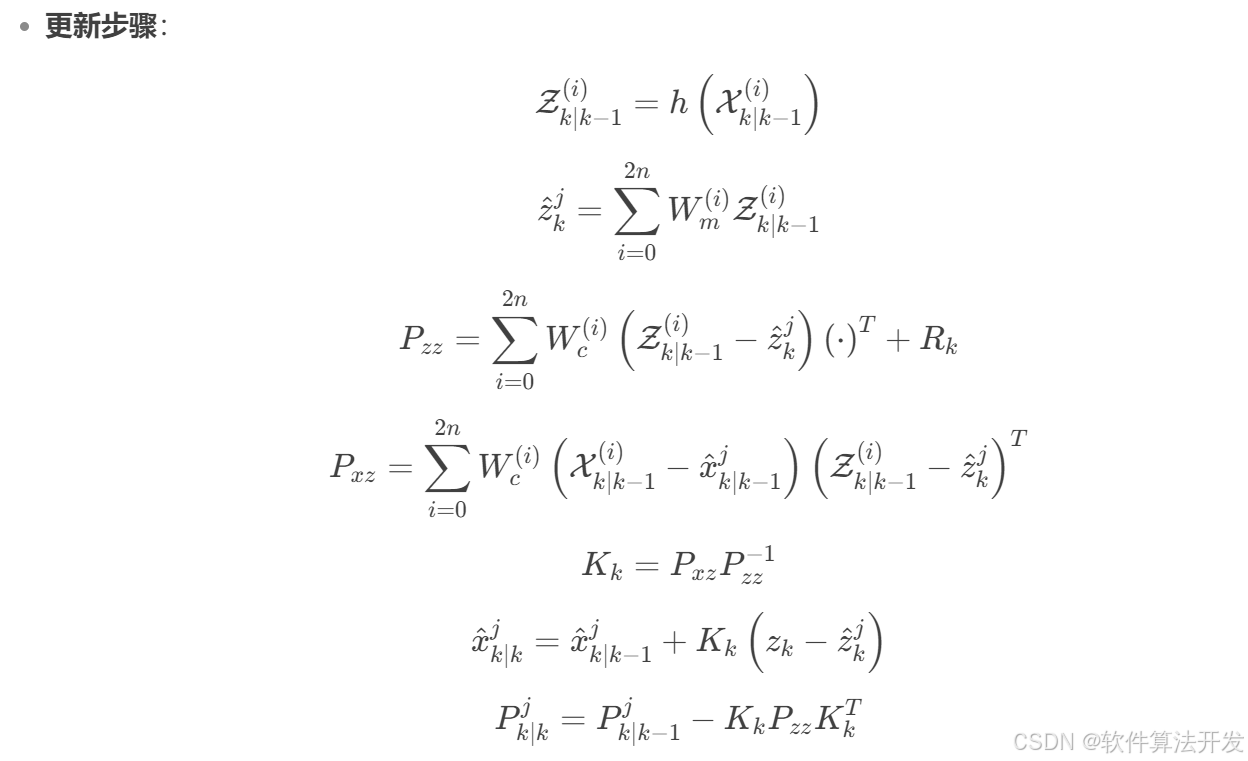


5.完整程序
VVV


