雙紐線周率與算術幾何平均

彭道意

2012年11月23日

雙紐線 $(x^2+y^2)^2=a^2(x^2-y^2)$ 時常出現在我們教材的例題或課后習題中, 鑒于此, 這篇短文主要介紹雙紐線周長的計算. 也是橢圓周長的計算一文的后續.

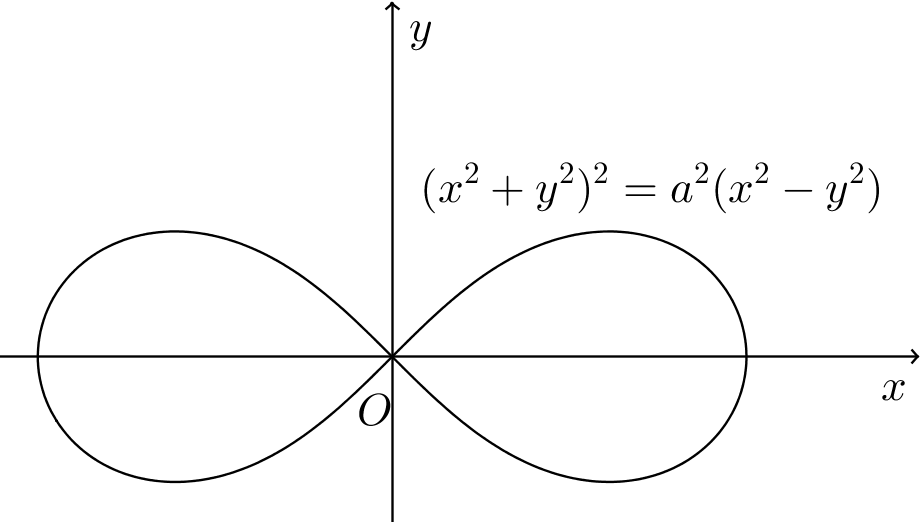
雙紐線也稱伯努利雙紐線 (Lemniscate of Bernoulli): $(x^2+y^2)^2=a^2(x^2-y^2)$ 的極坐標方程為 $r^2(\theta)=a^2\cos 2\theta$. 由曲線的弧長公式 (數學分析$\cdot$上 p254): \[s=\int_{\alpha}^{\beta}\sqrt{r^2(\theta)+r'^2(\theta)}\,\mathrmw0obha2h00\theta\] 結合雙紐線的對稱性, 設 $\varpi$ 是雙紐線的半周長, 且 $a=1$ 我們易得

\begin{align*}
2\varpi & = 4 \int_{0}^{\frac{\pi}{4}}\sqrt{r^2(\theta)+r'^2(\theta)}\,\mathrmw0obha2h00\theta \\
& =4\int_{0}^{\frac{\pi}{4}}\frac{\mathrmw0obha2h00\theta}{\sqrt{\cos 2\theta}} \\
& =4\int_{0}^{1}\frac{\mathrmw0obha2h00t}{\sqrt{1-t^4}}\quad (t^2=\cos 2\theta)
\end{align*}

在此積分中作變量代換 $t=u^{\frac{1}{4}}$ 則有 \begin{align*} \varpi & =\frac{1}{2}\int_{0}^{1}u^{-\frac{3}{4}}(1-u)^{-\frac{1}{2}}\,\mathrmw0obha2h00u \\ & =\frac{1}{2}{\rm B}\left(\frac{1}{4},\frac{1}{2}\right), \end{align*} 其中 ${\rm B}(p,q)$ 為 ${\rm B}$ 函數.

$\varpi$ 是 Gauss (1799 年) 由研究算術幾何平均時發現的量, 下面介紹 $\varpi$ 與算術幾何平均的關系.

當給出正數 $a\geqslant b$ 時, 由 $a_0=a,b_0=b$ 遞推地定義數列 $\{a_n\},\{b_n\}$ 如下: \[ \begin{cases} a_{n+1} & =\dfrac{a_n+b_n}{2}\quad \text{(算術平均)} \\ b_{n+1} & =\sqrt{a_nb_n}\quad \text{(幾何平均)}, \end{cases} \] 成立 $a_0\geqslant a_1\geqslant a_2\geqslant\cdots\geqslant b_2\geqslant b_1\geqslant b_0$ 及 \[|a_n-b_n|\leqslant \frac{a_0-b_0}{2^n},\] 于是得知 $\lim\limits_{n\to\infty}a_n=\lim\limits_{n\to\infty}b_n$. (數學分析$\cdot$上 p42 習題 11) 稱此極限值為$\text{算術幾何平均}$ (arithmetico-geometric mean), 以 $\mathrm{AGM}(a,b)$ 記之.

Gauss 發現的是 \[{\rm AGM}(\sqrt{2},1)=\frac{\pi}{\varpi}\] 這個等式. 更一般地 Gauss 得到了 ${\rm AGM}(a,b)$ 的公式.

$\text{定理 (Gauss)}$ \[ \mathrm{AGM}(a,b)=\dfrac{\dfrac{\pi}{2}}{\displaystyle\int_{0}^{\frac{\pi}{2}}\frac{\mathrmw0obha2h00\theta}{\sqrt{a^2\cos^2\theta +b^2\sin^2\theta}}}. \] 證 將上式右端的倒數記為 $F(a,b).$ 以 $x=b\tan \theta$ 作替換, 有 \[F(a,b)=\frac{2}{\pi}\int_{0}^{+\infty}\frac{\mathrmw0obha2h00x}{\sqrt{(a^2+x^2)(b^2+x^2)}}= \frac{1}{\pi}\int_{-\infty}^{+\infty}\frac{\mathrmw0obha2h00x}{\sqrt{(a^2+x^2)(b^2+x^2)}}\] 進一步作替換 $y=\frac{1}{2}\big(x-\frac{ab}{x}\big)$ 則有 \[F(a,b)=\frac{1}{\pi}\int_{-\infty}^{+\infty}\frac{\mathrmw0obha2h00y}{\sqrt{((\frac{a+b}{2})^2+y^2)(ab+y^2)}} =F\left(\frac{a+b}{2},\sqrt{ab}\right).\] 因此有 \[F(a,b)=F(a_1,b_1)=F(a_2,b_2)=\cdots=F(a_n,b_n).\] 于是, 令 $\mathrm{AGM}(a,b)=\alpha$ 則 \[F(a,b)=\lim_{n\to\infty}F(a_n,b_n)=F(\alpha,\alpha)=\frac{2}{\pi}\int_{0}^{\frac{\pi}{2}}\frac{\mathrmw0obha2h00\theta} {\sqrt{\alpha^2\cos^2\theta+\alpha^2\sin^2\theta}}=\frac{1}{\alpha},\] 則知 $\mathrm{AGM}(a,b)=F(a,b)^{-1}.$ $\quad\Box$

特別地, 有 \begin{align*} \mathrm{AGM}(\sqrt{2},1)^{-1} & =\frac{2}{\pi}\int_{0}^{\frac{\pi}{2}}\frac{\mathrmw0obha2h00\theta}{\sqrt{1+\cos^2\theta}} =\frac{2}{\pi}\int_{0}^{1}\frac{\mathrmw0obha2h00t}{\sqrt{1-t^4}}\quad (t=\cos\theta) \\ & =\frac{\varpi}{\pi}. \end{align*} 由上面的結果, 我們作進一步計算 \[\mathrm{B}(p,q)=\frac{\Gamma(p)\Gamma(q)}{\Gamma(p+q)}\] 其證明如下. 由 \[\Gamma(p)=\int_{0}^{\infty}x^{p-1}\mathrm{e}^{-x}\,\mathrmw0obha2h00x,\quad\Gamma(q) =\int_{0}^{\infty}y^{q-1}\mathrm{e}^{-y}\,\mathrmw0obha2h00y \] 得到 \[\Gamma(p)\Gamma(q)=\int_{0}^{\infty}\int_{0}^{\infty}x^{p-1}y^{q-1}\mathrm{e}^{-(x+y)}\,\mathrmw0obha2h00x\mathrmw0obha2h00y.\] 對其作變量替換 \[\begin{cases} x=ut \\ y=(1-u)t \end{cases} u\in[0,1],\ t\in[0,+\infty),\] 則 \begin{align*} \Gamma(p)\Gamma(q) & =\int_{0}^{1}\mathrmw0obha2h00u\int_{0}^{\infty}t\,\mathrmw0obha2h00t\cdot u^{p-1}(1-u)^{q-1}t^{p+q-2}\mathrm{e}^{-t} \\ & =\mathrm{B}(p,q)\Gamma(p+q). \end{align*} 因此有 \[\varpi=\frac{1}{2}\frac{\Gamma(\frac{1}{4})\Gamma(\frac{1}{2})}{\Gamma(\frac{3}{4})}.\] 再由余元公式 (Euler's reflection formula) \[\Gamma(s)\Gamma(1-s)=\frac{\pi}{\sin \pi s}\] 及 $\Gamma(\frac{1}{2})=\sqrt{\pi}$ 便求出了 \[\varpi=\frac{1}{2}\pi^{\frac{1}{2}}\Gamma\Big(\frac{1}{4}\Big)^2\frac{1}{\Gamma(\frac{1}{4})\Gamma(\frac{3}{4})} =2^{-\frac{3}{2}}\pi^{-\frac{1}{2}}\Gamma\Big(\frac{1}{4}\Big)^2.\]

綜合上述, 我們可用 $\Gamma$ 函數 ($\mathrm{B}$ 函數) 表示了雙紐線的周長. 并且指出了它與算術幾何平均的關系.