[概率論與數理統計]筆記：5.3 置信區間

記錄置信區間的相關概念，以及關于正態總體參數的置信區間的公式總結。

5.3 置信區間

前言

點估計無法提供其估計的誤差，而區間估計可以。

案例：“某人的月薪比2k多，比20k少”，這就是一個區間估計。

區間估計的好壞有兩個衡量指標：

區間長度
真實值落在該區間的概率

我們希望區間長度足夠小，而真實值落在該區間的概率又足夠大。

事實上，這兩個指標是矛盾的，如果概率很大，會導致區間變大；如果區間長度變小，落在區間內的概率就會變小。

定義

\[P\{\underline{\theta}<\theta<\overline{\theta}\}=1-\alpha \]

\(\theta\)是要估計的參數。
\((\underline{\theta},\overline{\theta})\)是置信區間，其中\(\underline{\theta}\)是置信下限，\(\overline{\theta}\)是置信上限。
\(1-\alpha\)是置信水平，或者叫置信度。

做題的時候一般是題目告知置信度，然后需要求解置信上下限。

表述

\((\underline\theta,\overline\theta)\)能套住\(\theta\)的概率是\(1-\alpha\)。

這里需要區分兩種表述：

\((\underline\theta,\overline\theta)\)能套住\(\theta\)的概率是\(1-\alpha\)。
\(\theta\) 落在 \((\underline\theta,\overline\theta)\)的概率是\(1-\alpha\)。

需要明確的是，\(\theta\)雖然是未知的，但是是確定的。\(\theta\)準確地固定在數軸上的一個位置，只是我們不知道在哪里。我們使用區間\((\underline\theta,\overline\theta)\)來做多次試驗，每次試驗的區間是隨機的不同的，因此\(\theta\)有時會被區間套住，有時候不會。

因此，我們使用的表述是套住，而不是落在。后者是針對不確定的值時候的表述。

樞軸變量

定義

為了求解置信區間，需要構造樞軸變量

\[I=I(T,\theta) \]

其中\(\theta\)是未知參數，\(T\)是已知的，\(I\) 的分布已知且與\(\theta\)無關。

對于給定的\(1-\alpha\)，確定\(F\)的上\(\frac{\alpha}{2}\)分位數，記為\(u_{\frac{\alpha}{2}}\)；確定\(F\)的上\((1-\frac{\alpha}{2})\)分位數，記為\(u_{1-\frac{\alpha}{2}}\)，那么就會有

\[P\{u_{1-\frac{\alpha}{2}}<I(T,\theta)<u_{\frac{\alpha}{2}}\}=1-\alpha \]

圖解

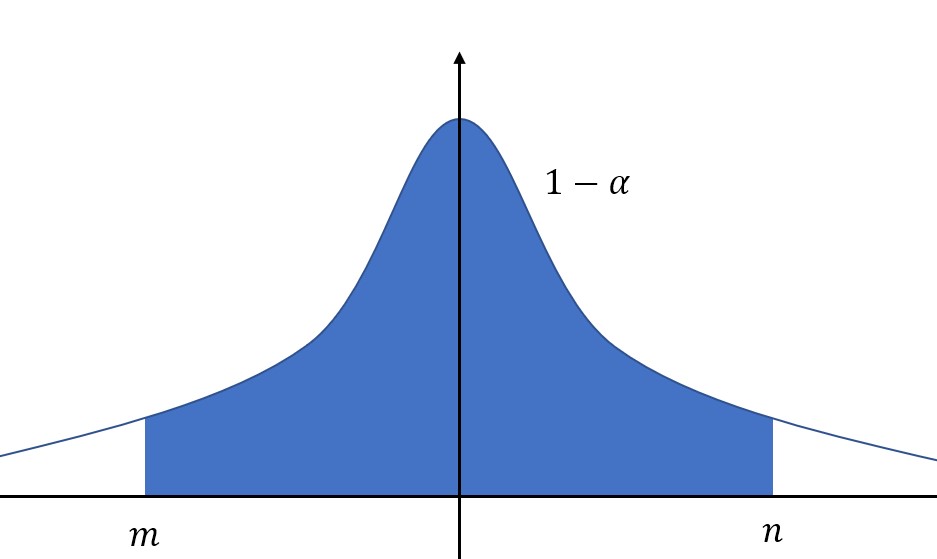
對于給定的置信度，也就是概率\(1-\alpha\)，我們的目的是求解區間上下限，也就是圖中的\(m\)和\(n\)。

值得注意的是，我們希望區間長度小一些，如果研究的分布是正態分布，或者密度函數類似于上圖，那么在置信度一定的情況下，即圖中藍色區域面積一定，只要選定區間位于中間，關于\(y\)軸對稱，那么區間長度就是最小的。（因為峰值在中間）

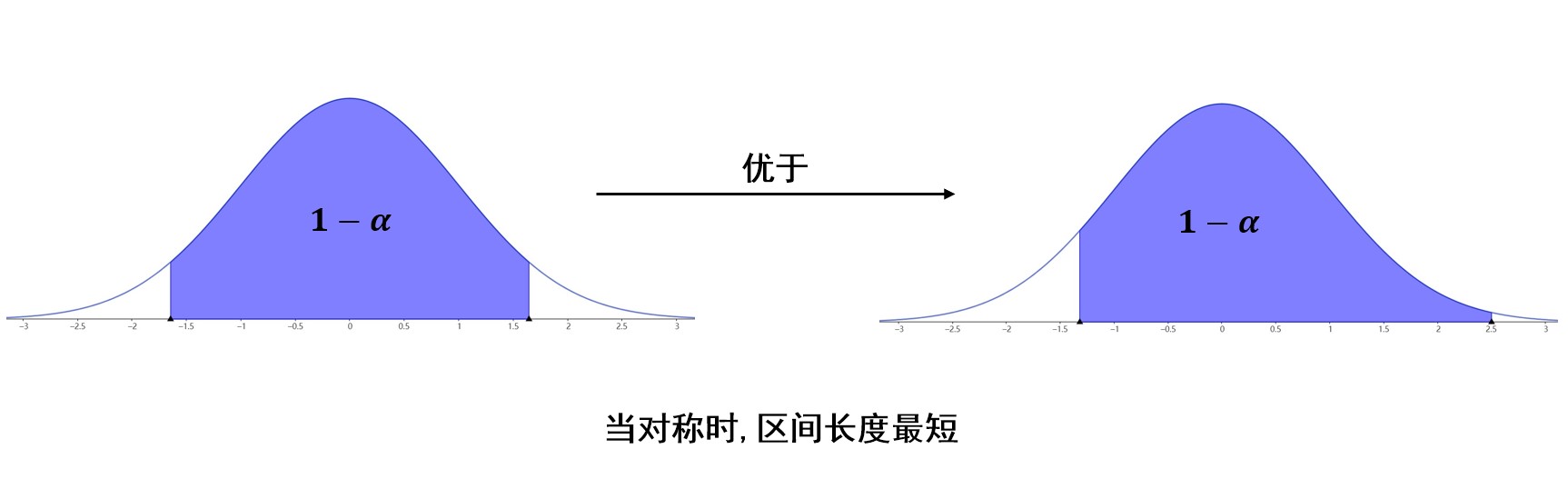
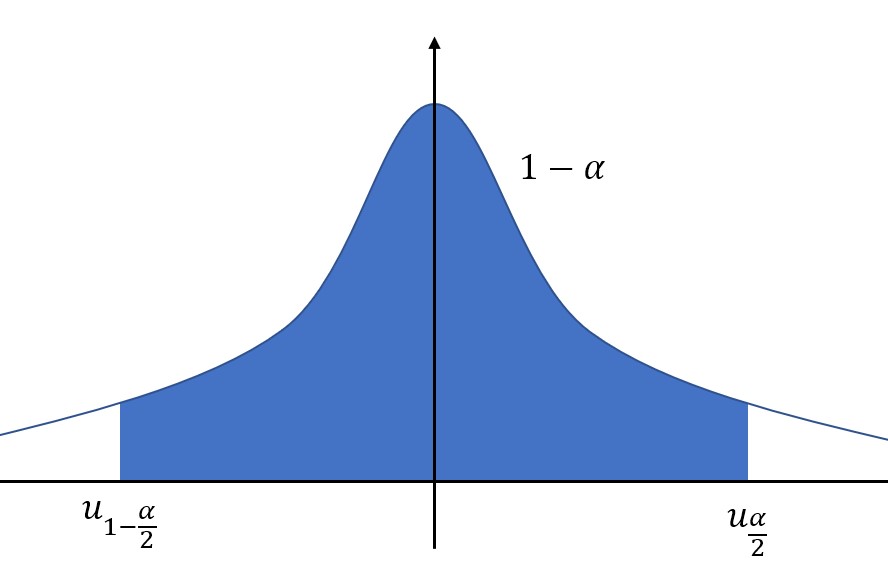
當置信區間位于中間時，置信度為\(1-\alpha\)，那么左右兩個置信上下限就可以通過上側分位數表示了。

中間的陰影面積為\(1-\alpha\)，那么左右兩側的空白面積就分別是\(\frac{\alpha}{2}\)。

置信上限使用上側分位數表示就是：\(u_{\frac{\alpha}{2}}\).

置信下限使用上側分位數表示就是：\(u_{1-\frac{\alpha}{2}}\).

總結

構造樞軸變量的目的是為了求解置信區間，將樞軸變量構造成我們熟悉的分布，比如正態分布，\(t\)分布，\(F\)分布。然后就可以利用這些分布的性質列出不等式，然后求解出我們要估計的參數的區間。

需要注意的是，樞軸變量只能包含一個未知的參數，即我們要估計的參數\(\theta\)，只有這樣才能進行不等式化簡。

正態總體參數的置信區間

均值\(\mu\)的置信區間

情況1：方差\(\sigma^2\)已知

總體方差\(\sigma^2\)已知，估計\(\mu\)，此時\(\mu\)是未知參數。

構造樞軸量：

\[U=\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\sim N(0,1) \]

相關知識點：??抽樣分布相關的定理的推論.

注：對于樞軸量\(U\)來說

\(\overline{X}\)和\(\sqrt{n}\)由樣本可以知道，是已知的。
\(\sigma\)由于總體方差\(\sigma^2\)已知，所以也是已知的。
\(U\)已知服從標準正態分布，該分布與未知參數\(\mu\)無關。

\(U\)服從標準正態分布，具有對稱性。

對于給定的置信度\(1-\alpha\)，可以計算得到\(\frac{\alpha}{2}\)，查表就可以得到上側分位數\(u_{\frac{\alpha}{2}}\)的值，再根據對稱性，就有

\[P\{-u_{\frac{\alpha}{2}}<\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}<u_{\frac{\alpha}{2}} \}=1-\alpha \]

于是就可以求解出\(\mu\)的置信區間：

\[\overline{X}-\frac{\sigma u_{\frac{\alpha}{2}}}{\sqrt{n}} < \mu < \overline{X}+\frac{\sigma u_{\frac{\alpha}{2}}}{\sqrt{n}} \]

理解：

如果增大置信度\(1-\alpha\)，那么\(\alpha\)就會變小，于是上側分位數\(u_{\frac{\alpha}{2}}\)會變大，代入上面的置信區間公式，就會發現置信上限變大了，置信下限變小了，即置信區間的區間長度變大了。
觀察到樣本容量\(n\)位于分母位置，于是發現樣本數增加可以縮小置信區間的區間長度。但是需要注意的是實際調研中，收集樣本是需要投入時間和金錢的，更多的樣本意味著更高的成本。

做題思路：代入已知數值求解區間上下限就行了??.

情況2：方差\(\sigma^2\)未知

總體方差\(\sigma^2\)未知，那么在構造樞軸變量的時候可以轉而使用樣本方差\(S^2\).

構造樞軸變量：

\[T=\frac{\overline{X}-\mu}{S/\sqrt{n}}\sim t(n-1) \]

相關知識點：??抽樣分布相關的定理

其中的\(S\)是樣本標準差。

由于\(t\)分布是具有對稱性的，對于給定的置信度\(1-\alpha\)，有

\[P\{ -t_{\frac{\alpha}{2}}(n-1) < \frac{\overline{X}-\mu}{S/\sqrt{n}} < t_{\frac{\alpha}{2}}(n-1) \} =1-\alpha \]

同理可解得置信區間為

\[\overline{X}-\frac{S}{\sqrt{n}}t_{\frac{\alpha}{2}}(n-1) < \mu < \overline{X}+\frac{S}{\sqrt{n}}t_{\frac{\alpha}{2}}(n-1) \]

\(t_{\frac{\alpha}{2}}(n-1)\)是自由度為\(n-1\)的\(t\)分布的上側\(\frac{\alpha}{2}\)分位數，可以通過查表得到。

方差\(\sigma^2\)的置信區間

情況1：均值\(\mu\)已知

構造樞軸變量：

\[\frac{1}{\sigma^2}\sum\limits_{i=1}^n(X_i-\mu)^2 \sim \chi^2(n) \]

相關知識點：??抽樣分布相關的定理

該樞軸變量只有總體方差\(\sigma^2\)是未知的。

注：卡方分布不是對稱的，但是由于習慣，在選擇上側分位數的時候仍然使用選擇\(\frac{\alpha}{2}\)，但是不能像正態分布或者\(t\)分布一樣直接使用相反數（比如上面的\(t_{\frac{\alpha}{2}}(n-1)\)和\(-t_{\frac{\alpha}{2}}(n-1)\)），而是要使用\(\chi^2_{1-\frac{\alpha}{2}}(n)\)和\(\chi^2_{\frac{\alpha}{2}}(n)\).

\[\chi^2_{1-\frac{\alpha}{2}}(n) < \frac{1}{\sigma^2}\sum\limits_{i=1}^n(X_i-\mu)^2 < \chi^2_{\frac{\alpha}{2}}(n) \]

可以解得：

\[\frac{\sum\limits_{i=1}^n(X_i-\mu)^2}{\chi^2_{\frac{\alpha}{2}}(n)} < \sigma^2 < \frac{\sum\limits_{i=1}^n(X_i-\mu)^2}{\chi^2_{1-\frac{\alpha}{2}}(n)} \]

情況2：均值\(\mu\)未知

總體均值\(\mu\)未知，轉而使用樣本均值\(\overline{X}\)構造樞軸變量：

\[\frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1) \]

相關知識點：??抽樣分布定理 2

由于樣本是已知的，所以樣本容量\(n\)和樣本方差\(S^2\)都是已知的，只有要估計的\(\sigma^2\)是未知的。

類似地，對于給定的置信度\(1-\alpha\)，計算上側分位數\(\chi^2_{1-\frac{\alpha}{2}}(n-1)\)和\(\chi^2_{\frac{\alpha}{2}}(n-1)\).

于是有

\[P\{ \chi^2_{1-\frac{\alpha}{2}}(n-1) < \frac{(n-1)S^2}{\sigma^2} < \chi^2_{\frac{\alpha}{2}}(n-1) \} = 1-\alpha \]

可以解得：

\[\frac{(n-1)S^2}{\chi^2_{\frac{\alpha}{2}}(n-1)} < \sigma^2 < \frac{(n-1)S^2}{\chi^2_{1-\frac{\alpha}{2}}(n-1)} \]

總結

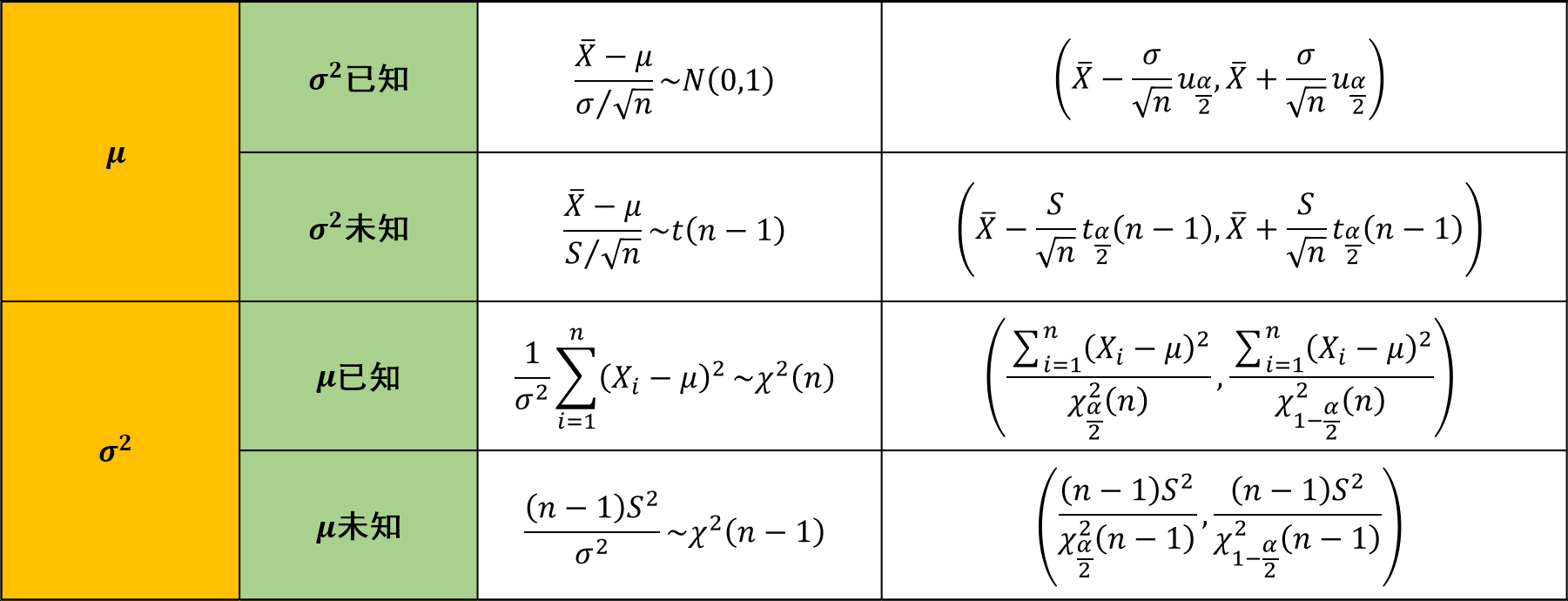
置信區間6

使用教材：
《概率論與數理統計》第四版中國人民大學龍永紅主編高等教育出版社

posted @ 2023-01-31 18:43 feixianxing 閱讀(5920) 評論(0) 收藏舉報

刷新頁面返回頂部

feixianxing