在并行處理器設計中，我們希望最大化訪存吞吐，讓更多的數據分布在不同的 bank，而非在一個 bank 中產生堵塞。一種場景是面對多應用并行，這往往可以通過劃分上下文基地址隔離；而另一種場景則是高并行同一個數據共用基地址，本文針對該場景下常見情形 Tensor Data Layout 進行討論。本文旨在針對硬件設計者介紹從數據邏輯到物理實現完整映射關系，其中很多推導過程比較繁瑣，如果是編程實踐中大致記得 row-major, col-major, swizzle data layout 幾種常見 layout 即可。

高維數據組織：從邏輯表示到物理表示

假設有 B 個深度為 D 寬度為 W 的 bank，其最小單位可用一個三維向量 \(P\) 表示，比如 \((10, 2,4)\) 表示訪問 bank=2, depth=10 那一地址中的第 width=4 個 scalar，scalar 粒度可根據需要設置，常見尋址用 byte。引入轉置表示以統一向量用列向量表示，便于后續公式推導。

其中 depth , bank , width 三個維度地位并不對稱，depth 需要多個時間周期來訪問不同 depth，而 bank 和 width 存在空間上的并行性，因此定義 \(P_{s}=[bank,width]^T\) 以便后續分析。RAM 是一種通過犧牲在 depth 上的并行讀取從而節約讀寫外圍電路面積開銷進而實現高密度存儲數據的結構，以時間換空間，恰恰適應程序數據生存周期很長，但調用次數相對稀疏的特點。

定義三維向量到地址的映射關系是 \(f\)，即 ：

常見映射關系為 \(Addr=f(P)=[S_w0obha2h00,S_{b},S_{w}]\cdot P=[W \times B,W,1]\cdot P\)，單從表達式看 \(f\) 并非存在唯一逆映射，考慮 \(P\) 每個元素的取值范圍以及所有都是整數，存在唯一逆映射 \(f^{-1}\)。這里的地址是相對前文定義 scalar 粒度而言，并非 SRAM 的地址控制信號， SRAM 的地址控制信號為 \(P_{b}=[depth, bank]^T\)。為了設計方便起見，\(D,B,W\) 都會設計為 2 的倍數，因此可以直接從 Addr 截取相應的 bit 表示對應的選擇關系。按照 bit 排列的順序，分為 high-order interleaving 和 low-order interleaving^[1]。

一個 N 維個張量數據 \(X\in R^N\) 中每個元素存在一個 N 維向量 \(I\in R^1\) 用于索引，定義其與地址的映射關系為：

比如二維矩陣索引 \(I=[row, col]^T\) Row-Major 映射關系定義為 \(Addr=g(I)=Base + Offset = Base + [COL, 1]\cdot I\)，而 Col-Major 映射關系定義為 \(Addr=Base + Offset = Base + [1,ROW]\cdot I\)。由于同一個數據往往共用一個基地址，普遍討論的 data layout 一般指 offset 和 \(I\) 之間關系。至此，我們可定義數據邏輯表示到存儲物理表示的函數關系：

計算單元-Layout 耦合策略

SIMD 計算單元往往存在一個特定的邏輯并行順序，比如每個 PE 是一個乘法累加器的 Output Stationary 的脈動陣列，計算 (T,I) (O,I) -> (T,O) 的 GEMM 運算，每個周期 input feature 需要在 T 維度并行數據，weight 需要在 O 維度并行的數據。

在 NVIDIA GPU 上，矩陣乘法 \(D=AB+C\) 可調用 wmma 或者 mma 指令完成，以 wmma 為例，分為三個階段 PTX 指令組合完成

• wmma.load 從 memory load 源操作數 \(A,B,C\) 每個操作數都要寫一條 ptx 指令，可指定原操作數來自 global memory 或 shared memory ^[2]
• wmma.mma 進行 GEMM 計算
• wmma.store 將 D 保存到 memory 中

雖然 load 支持顯式指定 A、B 、C 不同的 layout，但特定的 data layout 下似乎會發生 bank serialization^[3][4]。猜測 GPU 是先將任意的 data-layout 以特點的 layout 順序加載到 register file 中，如果發生 bank serialization 是在 load 階段而非 mma 階段。

計算單元對特定的 data layout 需求來自于 SIMD 并行 PE 之間的物理互聯-邏輯運算映射關系，反過來說，如果能夠在計算單元實現某種 reconfigurable 控制流&互聯重構，就可以對數據存儲 layout 具有一定魯棒。進一步討論存在兩種策略，一種是則是前文所述的計算單元 reconfigurable，一種是在存儲上實現 layout 魯棒，具體表現是程序員-編譯器的 layout 設計和 bank 之間的 NoC 網絡。由于處理器中往往存在多個計算單元而通過統一的存儲共享上下文，一般往往使得計算單元和 layout 耦合，將復雜度轉移到共用的存儲通路設計上。 感性計算舉個例子，假設一個處理器中有 N 個計算單元和一個共用 buffer，實現重構的復雜度是 k>1 而不實現的復雜度是 1，計算單元 reconfigurable 的開發復雜度是 \(O(kN+1)\)，而存儲單元 NoC 的開發復雜度是 \(O(N+k)\)。

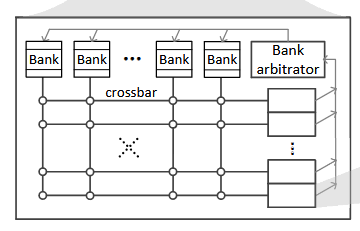
實現 NV 風格的較高魯棒訪問 register file，一是需要生成多個獨立的 bank 控制流，即等于 bank 數量的可編程的地址生成單元，據說 NV register file 是 4-bank dual port rf 設計^[5]，則一共是 8 個地址生成單元；二是需要給出 NoC 的控制信號，對于 \(N\) 輸入 \(M\) 輸出的 cross bar，一共需要 \(M\) 個 \(log_2(N)\) 比特控制信號，這部分最好也用一個可編程單元完成。對于 NoC 引發的 overhead ，之前的 blog ^[6]已經有過討論不再敘述。

Bank Conflict 的數學表達

假設計算單元單位周期對數據 layout 需求是 \(\{T_{0},T_{1},..., T_{N-1}\}\)，通過 \(f^{-1} \circ g\) 可得到對應物理存儲 \(\{P_{0},P_{1},...,P_{N-1}\}\) 進而得到 \(\{P_{s,0},P_{s,1},...,P_{s,N-1}\}\)。不產生 bank conflict 的定義是，這 N 個物理存儲表示在 \((bank, width)\) 維度上相同的個數小于等于相應讀寫端口數量（Dual-port, Two-port, Single-port），即集合 \(\{P_{s,0},P_{s,1},...,P_{s,N-1}\}\) 的“眾數”頻數小于等于端口數量。

舉例：傳統線性 Layout

對于 \(f\) 和 \(f^{-1}\)，其定義如下：

線性 layout 即 row-major 或 col-major， \(g\) 和 \(g^{-1}\) 定義如下：

則有：

一般來說，計算單元對于矩陣的訪存需求都是沿著某一個維度（而非對角線），即 \(I=c\times e_{1}+i \times e_{2}\) ，其中 \(e_{1}, e_{2}\) 是 row 或者 col 的單位向量，\(c\) 是一個常數，\(i\) 為各不相同的多個取值。附計算 bank conflict 示例代碼 ^[7]。

而 Swizzle Layout 則是跳過了中間地址轉換過程，直接構造 \(P\) 和 \(I\) 之間的數學關系，并基于 \(I=c\times e_{1}+i \times e_{2}\) 的假設，在 \(\{e_{1},e_{2}\}=\{e_{row}, e_{col}\}\) 或 \(\{e_{1},e_{2}\}=\{e_{col}, e_{row}\}\) 都有 \(P\) 各不相同，即對任意方向讀取都滿足 bank-free。