大家好~本文推導全連接層的前向傳播、后向傳播、更新權重和偏移的數學公式，其中包括兩種全連接層：作為輸出層的全連接層、作為隱藏層的全連接層。
神經網絡前向和后向傳播推導（一）：前向傳播和梯度下降
神經網絡前向和后向傳播推導（二）：全連接層
構建神經網絡
我們構建一個三層神經網絡，由一層輸入層+兩層全連接層組成：
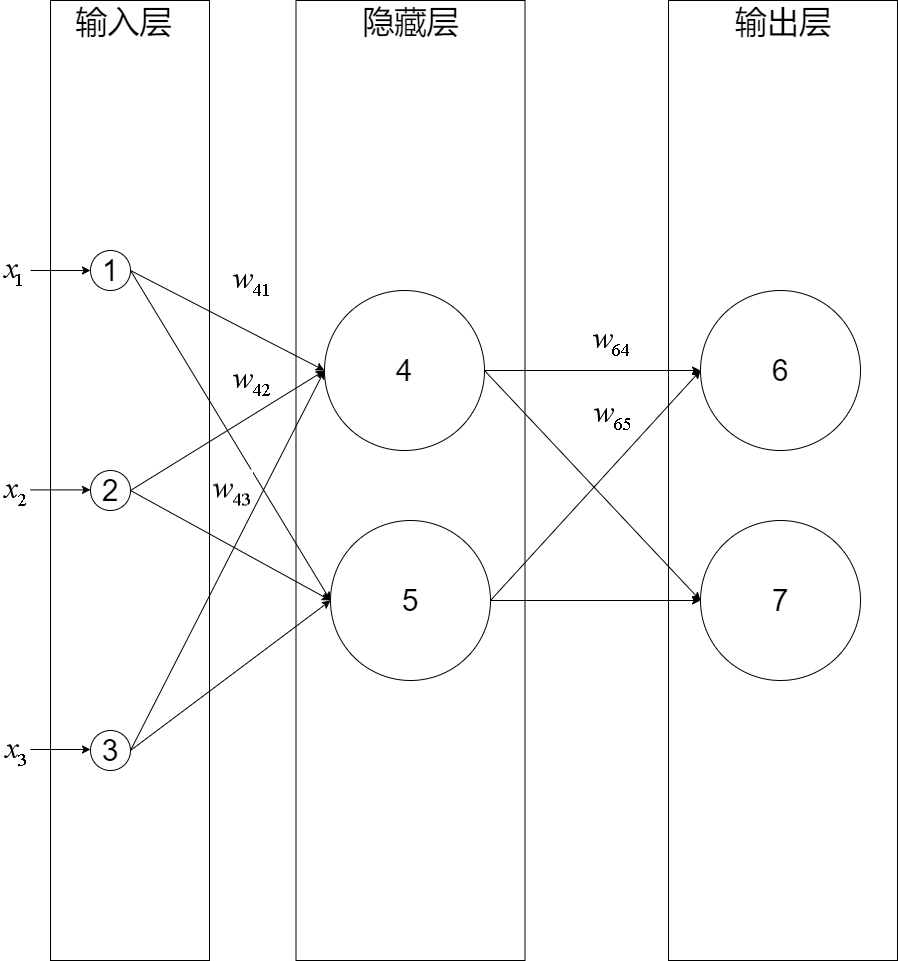
輸入層有三個節點，我們將其依次編號為1、2、3；隱藏層的兩個節點，編號依次為4、5；輸出層的兩個節點編號為6、7。因為我們這個神經網絡是全連接網絡，所以可以看到每個節點都和上一層的所有節點有連接。比如，我們可以看到隱藏層的節點4，它和輸入層的三個節點1、2、3之間都有連接，其連接上的權重分別為\(w_{41}, w_{42}, w_{43}\)
（注意：權重的序號的命名規則是下一層的序號在上一層的序號之前，如為\(w_{41}\)而不是\(w_{14}\)）
推導前向傳播
節點4的輸出值\(y_4\)的計算公式為：
\[y_4=f(\vec{w_4}^T\cdot\vec{x})
\]
其中：
\[\vec{w_4} = [w_{41}, w_{42}, w_{43}, w_{b_4}]
\]
\[\vec{x} =
\begin{bmatrix}
x_1\\
x_2\\
x_3\\
1 \\
\end{bmatrix}
\]
\[f為激活函數
\]
推導隱藏層的前向傳播
我們把隱藏層的權重向量組合在一起成為矩陣，就推導出隱藏層的前向傳播計算公式了：
\[\overrightarrow{y_{隱藏層}}=f(W_{隱藏層}\cdot\vec{x})
\]
其中：
\[W_{隱藏層} = \begin{bmatrix}
\vec{w_4} \\
\vec{w_5} \\
\end{bmatrix} =\begin{bmatrix}
w_{41}, w_{42}, w_{43}, w_{b_4} \\
w_{51}, w_{52}, w_{53}, w_{b_5} \\
\end{bmatrix}
\]
\[\vec{x} =
\begin{bmatrix}
x_1\\
x_2\\
x_3\\
1 \\
\end{bmatrix}
\]
\[\overrightarrow{y_{隱藏層}}=\begin{bmatrix}
y_4 \\
y_5 \\
\end{bmatrix}
\]
推導輸出層的前向傳播
同理，可推出輸出層的前向傳播計算公式：
\[\overrightarrow{y_{輸出層}}=f(W_{輸出層}\cdot\overrightarrow{y_{隱藏層}})
\]
其中：
\[W_{輸出層} = \begin{bmatrix}
\vec{w_6} \\
\vec{w_7} \\
\end{bmatrix} =\begin{bmatrix}
w_{64}, w_{65}, w_{b_6} \\
w_{74}, w_{75}, w_{b_7} \\
\end{bmatrix}
\]
\[\overrightarrow{y_{隱藏層}} =
\begin{bmatrix}
y_4 \\
y_5 \\
1 \\
\end{bmatrix}
\]
\[\overrightarrow{y_{輸出層}}=\begin{bmatrix}
y_6 \\
y_7 \\
\end{bmatrix}
\]
推導后向傳播
我們先來看下輸出層的梯度下降算法公式：
\[w_{kj}=w_{kj}-\eta\frac{dE}{dw_{kj}}
\]
其中：\(k\)是輸出層的節點序號，\(j\)是隱藏層的節點序號，\(w_{kj}\)是輸出層的權重矩陣\(W_{輸出層}\)的權重值，\(\frac{dE}{dw_{kj}}\)是節點k的梯度
設\(net_k\)函數是節點k的加權輸入：
\[net_k=\overrightarrow{w_k}^T\cdot\overrightarrow{y_{隱藏層}} = \sum_{j} w_{kj}y_j
\]
因為\(E\)是\(\overrightarrow{y_{輸出層}}\)的函數，\(\overrightarrow{y_{輸出層}}\)是\(net_k\)的函數，\(net_k\)是\(w_{kj}\)的函數，所以根據鏈式求導法則，可以得到：
\[\begin{aligned}
\frac{dE}{dw_{kj}} & = \frac{dE}{dnet_k}\frac{dnet_k}{dw_{kj}} \\
& = \frac{dE}{dnet_k}\frac{d\sum_{j} w_{kj}y_{j}}{dw_{kj}} \\
& = \frac{dE}{dnet_k}y_{j} \\
\end{aligned}
\]
定義節點k的誤差項\(\delta_k\)為：
\[\delta_k = \frac{dE}{dnet_k}
\]
因為\(y_{j}\)已知，所以只要求出\(\delta_k\)，就能計算出節點k的梯度
同理，對于隱藏層，可以得到下面的公式：
\[w_{ji}=w_{ji}-\eta\frac{dE}{dw_{ji}} \\
\frac{dE}{dw_{ji}} = \frac{dE}{dnet_j}x_{i} \\
\delta_j = \frac{dE}{dnet_j}
\]
其中：\(j\)是隱藏層的節點序號，\(i\)是輸入層的節點序號，\(w_{ji}\)是隱藏層的權重矩陣\(W_{隱藏層}\)的權重值，\(\frac{dE}{dw_{ji}}\)是節點j的梯度
因為\(x_{i}\)已知，所以只要求出\(\delta_j\)，就能計算出節點j的梯度
推導輸出層的\(\delta_k\)
因為節點k的輸出值\(y_k\)作為\(\overrightarrow{y_{輸出層}}\)的一個值，并沒有影響\(\overrightarrow{y_{輸出層}}\)的其它值，所以節點k直接影響了\(E\)。也就說
因為\(E\)是\(y_k\)的函數，\(y_k\)是\(net_k\)的函數，所以根據鏈式求導法則，可以得到：
\[\delta_k=\frac{dE}{dnet_k} = \frac{dE}{dy_k}\frac{dy_k}{dnet_k}
\]
上式的第一項等于：
\[\frac{dE}{dy_k} = \frac{dE(\overrightarrow{y_{輸出層}})}{dy_k}
\]
上式的第二項即為求激活函數\(f\)的導數：
\[\frac{dy_k}{dnet_k} = \frac{df(net_k)}{dnet_k}
\]
將第一項和第二項帶入\(\frac{dE}{dnet_k}\)，得到：
\[\delta_k = \frac{dE(\overrightarrow{y_{輸出層}})}{dy_k}\frac{df(net_k)}{dnet_k}
\]
只要確定了\(E\)和激活函數\(f\)，就可以求出\(\delta_k\)
一般來說，\(E\)可以為\(softmax\)，\(f\)可以為\(relu\)
推導隱藏層的\(\delta_j\)
因為節點j的輸出值\(y_j\)作為輸出層所有節點的一個輸入值，影響了\(\overrightarrow{y_{輸出層}}\)的每個值，所以節點j通過輸出層所有節點影響了\(E\)。也就說\(E\)是輸出層所有節點的\(net\)的函數，每個\(net\)函數\(net_k\)都是\(net_j\)的函數，所以根據全導數公式，可以得到：
\[\begin{aligned}
\delta_j =\frac{dE}{dnet_j} & = \sum_{k\in{輸出層}} \quad\frac{dE}{dnet_k}\frac{dnet_k}{dnet_j} \\
& = \sum_{k\in{輸出層}} \quad\delta_k\frac{dnet_k}{dnet_j}
\end{aligned}
\]
因為\(net_k\)是\(y_{j}\)的函數，\(y_{j}\)是\(net_j\)的函數，所以根據鏈式求導法則，可以得到：
\[\begin{aligned}
\frac{dnet_k}{dnet_j} & = \frac{dnet_k}{dy_{j}}\frac{dy_{j}}{dnet_j} \\
& = \frac{d\sum_{j} w_{kj}y_{j}}{dy_{j}}\frac{dy_{j}}{dnet_j} \\
& = w_{kj}\frac{dy_{j}}{dnet_j} \\
& = w_{kj}\frac{df(net_j)}{dnet_j} \\
\end{aligned}
\]
代入，得：
\[\delta_j = \sum_{k\in{輸出層}} \quad\delta_k w_{kj}\frac{df(net_j)}{dnet_j}
\]
只要確定了激活函數\(f\)和得到了每個\(\delta_k\)，就可以求出\(\delta_j\)
后向傳播算法
通過上面的推導，得知要推導隱藏層的\(\delta_j\)，需要先得到出下一層（也就是輸出層）每個節點的誤差項\(\delta_k\)
這就是反向傳播算法：需要先計算輸出層的誤差項，然后反向依次計算每層的誤差項，直到與輸入層相連的層
推導權重和偏移更新
經過上面的推導，可以得出輸出層的更新公式為：
\[\begin{aligned}
w_{kj} =w_{kj}-\eta\delta_k y_j
\end{aligned}
\]
隱藏層的更新公式為：
\[\begin{aligned}
w_{ji} & =w_{ji}-\eta\delta_j x_i
\end{aligned}
\]
總結
我們在推導隱藏層的誤差項時，應用了全導數公式，這是一個難點
參考資料
零基礎入門深度學習 | 第三章：神經網絡和反向傳播算法
大家好~本文推導全連接層的前向傳播、后向傳播、更新權重和偏移的數學公式，其中包括兩種全連接層：作為輸出層的全連接層、作為隱藏層的全連接層
浙公網安備 33010602011771號