大家好~本文介紹了前向傳播、梯度下降算法，總結了神經網絡在訓練和推理階段執行的步驟。

在后面的文章中，我們會從最簡單的神經網絡開始，不斷地增加不同種類的層（如全連接層等），推導每種層的前向傳播、后向傳播、梯度計算、權重和偏移更新的數學公式

神經網絡前向和后向傳播推導（一）：前向傳播和梯度下降
神經網絡前向和后向傳播推導（二）：全連接層

神經元

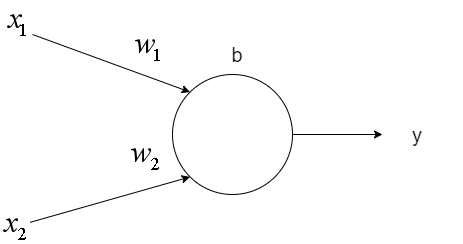
如上圖所示，一個神經元具有一個偏移值b和多個權重值w，接受多個輸入值x，返回一個輸出值y

計算公式為：

其中：

我們可以將\(b\)表示為\(w_b\)，合并到\(\vec{w}\)中；并且把\(y\)表示為向量。這樣就便于向量化編程
計算公式變為：

其中：

神經網絡

一個神經網絡由多層組成，而每層由多個神經元組成。
如下圖所示是一個三層神經網絡，由一層輸入層+兩層全連接層組成：

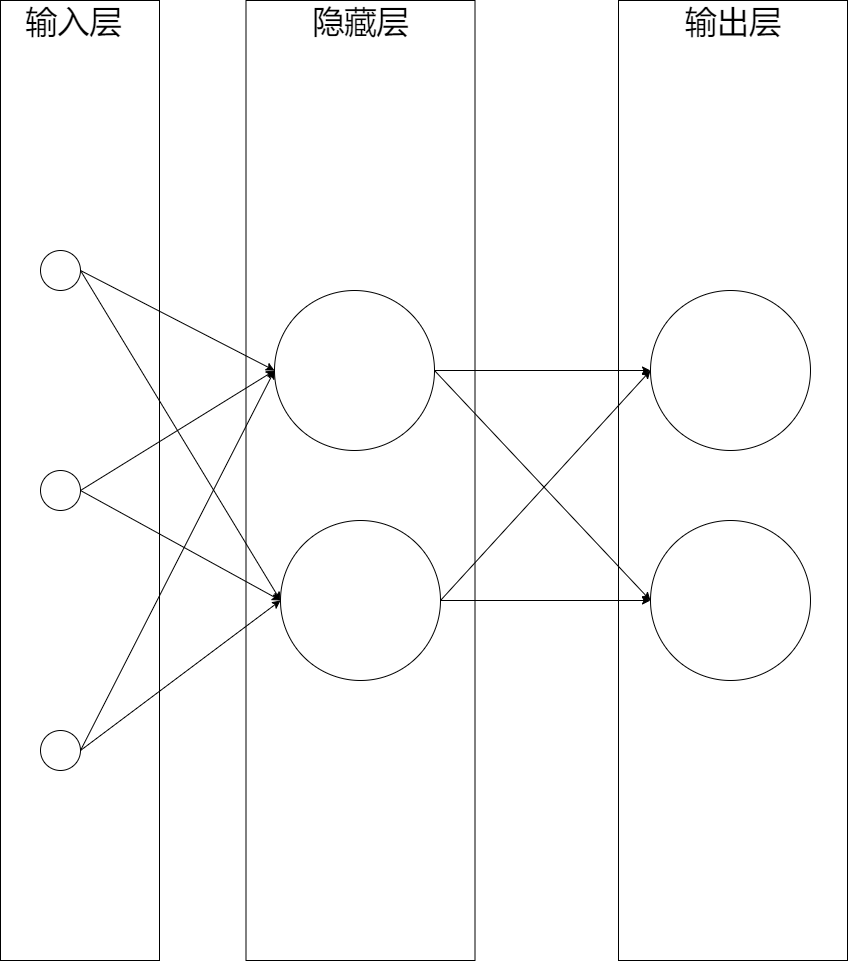
這個網絡中最左邊的層稱為輸入層，包含輸入神經元；最右邊的層稱為輸出層，包含輸出神經元；中間的層則被稱為隱藏層

本文以該神經網絡為例進行推導

前向傳播

從輸入層開始，輸入層的輸出作為隱藏層的輸入傳入隱藏層，計算出輸出：\(\overrightarrow{y_{隱藏層}}\)；
\(\overrightarrow{y_{隱藏層}}\)作為輸出層的輸入傳入輸出層，計算出輸出：\(\overrightarrow{y_{輸出層}}\)，作為整個網絡的輸出。

公式為：

其中：\(W\)為權重矩陣

這就是前向傳播算法，也就是從輸入層開始，依次傳入每層，直到輸出層，從而得到每層的輸出。

前向傳播用來做什么呢？它在訓練和推理階段都有使用：
在訓練階段，前向傳播得到了輸出層的輸出和其余各層的輸出，其中計算正確率需要前者，計算后向傳播需要前者和后者；
在推理階段，前向傳播得到了輸出層的輸出，作為推理的結果。比如根據包含一個人的體重、身高這樣的一個樣本數據，得到了這人是男人還是女人的輸出。

梯度下降

推理階段使用前向傳播得到輸出值，而前向傳播需要知道每層的權重和偏移。
為了在推理階段能夠得到接近真實值的輸出值，每層的權重和偏移應該是某個合適的值。那么合適的值應該是多少呢？
我們可以在訓練階段給每層一個初始的權重和偏移（比如說都設為0）；然后輸入大量的樣本，不斷地更新每層的權重和偏移，使得它們逐漸接近合適的值。
那么，什么值才是合適的值呢？
我們可以構建一個目標函數，用來在訓練階段度量輸出層的輸出值和真實值的誤差大小：

其中\(\overrightarrow{y_{輸出層}}\)為輸出層的輸出值，\(\overrightarrow{y_{真實}}\)為真實值，\(E\)為目標函數，\(e\)為誤差

當誤差\(e\)最小時，輸出層的輸出值就最接近真實值。因為\(E\)是輸出層的權重和偏移(\(\overrightarrow{w_{輸出層}}\)）)的函數（因為\(E\)是\(\overrightarrow{y_{輸出層}}\)的函數，而\(\overrightarrow{y_{輸出層}}\)又是\(\overrightarrow{w_{輸出層}}\)的函數，所以\(E\)是\(\overrightarrow{w_{輸出層}}\)的函數），所以此時的\(\overrightarrow{w_{輸出層}}\)就是合適的值

如何求\(E\)的最小值點呢？對于計算機來說，可以一步一步的去把函數的極值點試出來，如下圖所示：

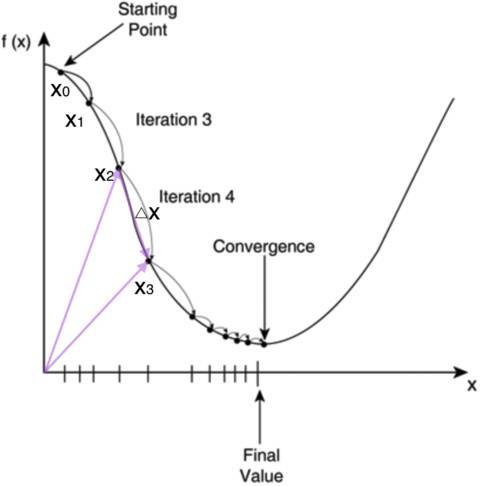
首先，我們隨便選擇一個點開始，比如上圖的\(x_0\)。接下來，每次迭代修改\(X\)為\(x_1, x_2, x_3\)......經過數次迭代后最終達到函數最小值點。

你可能要問了，為啥每次修改\(X\)，都能往函數最小值那個方向前進呢？這里的奧秘在于，我們每次都是向函數\(y=f(x)\)的梯度的相反方向來修改\(X\)。
什么是梯度呢？梯度是一個向量，它指向函數值上升最快的方向。顯然，梯度的反方向當然就是函數值下降最快的方向了。
我們每次沿著梯度相反方向去修改\(X\)，當然就能走到函數的最小值附近。
之所以是最小值附近而不是最小值那個點，是因為我們每次移動的步長不會那么恰到好處，有可能最后一次迭代走遠了越過了最小值那個點。步長的選擇是門手藝，如果選擇小了，那么就會迭代很多輪才能走到最小值附近；如果選擇大了，那可能就會越過最小值很遠，收斂不到一個好的點上。

按照上面的討論，我們就可以寫出梯度下降算法的公式：

其中\(\frac{df(x)}{dx}\)是梯度，\(\eta\)是步長，也稱作學習率

只要把\(f\)替換為\(E\)，\(X\)分別替換為\(W_{輸出層}\)、\(W_{隱藏層}\)，\(x_0\)分別替換為初始的\(\overrightarrow{w_{輸出層}}\)、初始的\(\overrightarrow{w_{隱藏層}}\)，就可以得到使\(E\)達到最小值的梯度下降算法的公式：

其中\(W_{輸出層new}\)為輸出層的權重矩陣，\(W_{隱藏層new}\)為隱藏層的權重矩陣，\(w_{輸出層}\)為輸出層的權重值，\(w_{隱藏層}\)為隱藏層的權重值，

總結

神經網絡的使用可以分成兩個階段：
訓練和推理

訓練階段

先進行前向傳播，得到每層的輸出；
然后進行后向傳播，根據每層的誤差項而計算出上一層的誤差項，并且計算每層的梯度（關于后向傳播詳見神經網絡前向和后向傳播推導（二）：全連接層->推導后向傳播）；
最后按照梯度下降算法，更新每層的權重和偏移。

可以用下面的公式來表達訓練：
每層的權重和偏移=訓練(大量的樣本)

其中\(W\)為包含每層的權重和偏移向量的矩陣

推理階段

使用訓練階段得到的每層的權重和偏移，進行前向傳播，得到輸出層的輸出作為推理結果。

可以用下面的公式來表達推理：

參考資料

零基礎入門深度學習 | 第二章：線性單元和梯度下降
零基礎入門深度學習 | 第三章：神經網絡和反向傳播算法