問題：

輸入N個0～9的整數(shù)，可以重復(fù)，從小到大打印出這N個數(shù)字組成的所有N位數(shù)。

e.g

輸入：

4002

輸出:

0024

0042

0204

0240

0402

0420

2004

2040

2400

4002

4020

4200

 

策略：

這道題是一個同學(xué)問我的，她幫一個同學(xué)完成作業(yè)。我剛看到問題的時候，第一個想法就是求出全排列，時間復(fù)雜度是O（n！）。寫個算法除去重復(fù)的數(shù)列，再寫一個算法排序，一個排序算法比如快速排序的平均時間復(fù)雜度O（n*lg n)。但也立馬否定了。這個算法在整數(shù)個數(shù)增加后空間復(fù)雜度、時間復(fù)雜度都會有巨大的增長。這個算法好理解，但也不夠巧妙。

 

其實可以考慮可以在尋找全排列的時候就可以以升序的順序輸出。因為升序數(shù)列數(shù)字的排列是有規(guī)律的。看下面的升序數(shù)列：

2345（1）

2354 （2）5提前到第3位

2435 （3）在（1）數(shù)列基礎(chǔ)上4提前到第2位

2453 （4）5提前了一個位置，似乎是（1）～(2)過程的重復(fù)

2534  （5）在（1）數(shù)列的基礎(chǔ)上將5提前到第2位

2543 （6）4提前了一個位置，似乎是（1）~(2)過程的重復(fù)，（5）～（6）似乎是（3）～（4）過程的重復(fù)

3245  （7）在（1）數(shù)列基礎(chǔ)上將3提前到第1位

3254  （8）5提前了一個位置，似乎是（1）～(2)過程的重復(fù)

 

3425  （9）在（7）數(shù)列的基礎(chǔ)上將4提前到第2位

3452  （10）將5提前到第3位，似乎是（1）～(2)過程的重復(fù)，（9）～（10）似乎是（3）～（4）過程的重復(fù)

 

 

3524  （11）在（7）數(shù)列基礎(chǔ)上將5提前到第2位

3542  （12）將4提前到第3位，似乎是（1）～(2)過程的重復(fù)，（11）～（12）似乎是（3）～（4）過程的重復(fù)

 

 

4235  （13）在（1）數(shù)列的基礎(chǔ)上將4提前到第一位

4253  （14）5提前了一個位置，似乎是（1）～(2)過程的重復(fù)

 

4325  （15）在（13）數(shù)列基礎(chǔ)上將3提前到第2位

4352  （16）將5提前到第3位，似乎是（1）～(2)過程的重復(fù)，（15）～（16）似乎是（3）～（4）過程的重復(fù)

4523  （17）在（13）數(shù)列基礎(chǔ)上將5提前到第2位

4532  （18）將3提前到第3位，似乎是（1）～(2)過程的重復(fù)，（17）～（18）似乎是（3）～（4）過程的重復(fù)，（13）～（18）似乎是（7）～（11）過程的重復(fù)

5234  （19）在（1）數(shù)列的基礎(chǔ)上將5提前到第一位

 

 

5243  （20）4提前了一個位置，似乎是（1）～(2)過程的重復(fù)

 

5324  （21）在（19）數(shù)列基礎(chǔ)上將3提前到第2位

5342  （22）將4提前到第3位，似乎是（1）～(2)過程的重復(fù)，（21）～（22）似乎是（3）～（4）過程的重復(fù)

5423  （23）在（19）數(shù)列基礎(chǔ)上將4提前到第2位

5432  （24）將3提前到第3位，似乎是（1）～(2)過程的重復(fù)，（23）～（24）似乎是（3）～（4）過程的重復(fù)，（19）～（24）似乎是（7）～（11）過程的重復(fù)

 

各位睿智的看官，看出來否？存在一個策略分解這個問題成小問題，而對于每個分解問題存在一個通用的策略擊破！對了，睿智如您，這就是分而治之的策略！將它問題分解成更小的問題，再分解成更小的問題。

（1）（2）是子數(shù)列4 5的全排列。

（1）～(6)是子數(shù)列3 4 5的全排列。（1）（2），（3）（4），（5）（6）分別是子數(shù)列3 5，3 4，4 5的全排列。

（1）～（24）是數(shù)列2 3 4 5的全排列。（1）～（6），（7）~(12),(13)～（18），（19）～（24）分別是3 4 5，2 4 5，2 3 5，2 3 4的全排列。下面就不列舉了額。。。

 

思考即可發(fā)現(xiàn)，對每個輸入的子數(shù)列，一個通用策略是：

1.從輸入數(shù)列的倒數(shù)第二位作為當(dāng)前位置開始到子數(shù)列開始處結(jié)束，迭代執(zhí)行第2步。

2.在當(dāng)前位置之后選擇一個合適的數(shù)字提前到當(dāng)前位置。（選擇數(shù)字的策略下面有描述）

3.將當(dāng)前位置之后的子數(shù)列作為輸入，轉(zhuǎn)入第1步，尋求子數(shù)列的全排列。

 

這是一個間接的遞歸調(diào)用，程序開始需要先將原始順序混亂的數(shù)列進行升序排序，之后作為輸入，調(diào)用第1步。可以發(fā)現(xiàn)，整個算法中子數(shù)列（注意此處指提前操作之后當(dāng)前位置之后的數(shù)列）在調(diào)用第1步時始終保持升序有序，以保證最后的輸出保持從小到大升序排列）。

 

注意是提前，不是交換，即不改變當(dāng)前位置之后的升序順序。

 

認真看下這個過程，便可以發(fā)現(xiàn)一個選擇到提前到當(dāng)前位置數(shù)字的策略。選擇之前數(shù)列在當(dāng)前位置之后總是升序排列的。為了使打印出的數(shù)列保持升序，選擇提前數(shù)字時應(yīng)當(dāng)從小到大選擇。然后將交換之后的目前位置之后的子數(shù)列遞歸調(diào)用，進行對它的全排列。還應(yīng)該考慮數(shù)列中出現(xiàn)重復(fù)數(shù)字的情況。在選擇數(shù)字時，應(yīng)當(dāng)保證提前到當(dāng)前位置的數(shù)字和當(dāng)前位置并且和前一個選擇的數(shù)字不同。這樣可以避免重復(fù)數(shù)列的出現(xiàn)。

 

每次提前數(shù)字應(yīng)當(dāng)在備份上進行處理，否則會造成混亂，違反了始終保持子數(shù)列升序有序的原則。其實當(dāng)N增大到很大時，其全排列的數(shù)目是驚人的，運行會有種刷屏的感覺，:-)。其空間復(fù)雜度和時間復(fù)雜度是很高的。

 

實現(xiàn)（C語言）：

#include<stdio.h> #include<assert.h> #define MAX_NUM 10 //最大長度，可更改 int numbers[MAX_NUM]; int length; void range(int number[],int st){//排序算法 int i,j; for(i=st;i<length;++i) for(j=st;j<length-1-i;++j) if(number[j]>number[j+1]){ int temp=number[j]; number[j]=number[j+1]; number[j+1]=temp; } } void p_full_arrangement(int[],int); void next_arrange(int in[],int pos){ //通過交換找到下一組局部有序的數(shù)列，對應(yīng)于解題通用策略的第2，3步 int i,cop[MAX_NUM]; for(i=pos+1;i<length;++i){ if(in[i]>in[pos]&&in[i]!=in[i-1]){ //防止出現(xiàn)重復(fù)數(shù)列的情況，避免與當(dāng)前位置或者與前一個選擇數(shù)字相同的數(shù)字交換 int j,t; for(t=0;t<length;++t) cop[t]=in[t]; //拷貝數(shù)列，在拷貝數(shù)列上進行處理 for(j=i;j>pos;j--){ //提前操作 int temp=cop[j]; cop[j]=cop[j-1]; cop[j-1]=temp; } p_full_arrangement(cop,pos+1); //將當(dāng)前位置之后的子數(shù)列得出全排序 } } } void p_full_arrangement(int in[],int pos){//將輸入的子數(shù)列得到全排列并且打印,對應(yīng)于解題通用策略中的第1步 int i; for(i=0;i<length;++i) printf("%d",in[i]); printf("/n"); for(i=length-2;i>pos-1;i--){ next_arrange(in,i); } } void full_arrangement(){//先將數(shù)列排序再調(diào)用全排列的算法 range(numbers,0); p_full_arrangement(numbers,0); } int main(){ int i; printf("Input the length:/n"); scanf("%d",&length); assert(length<=MAX_NUM);//通過斷言防止輸入的數(shù)列長度超出輸出的范圍 printf("Input the numbers:/n"); for(i=0;i<length;++i) scanf("%d",&numbers[i]); printf("The result:/n"); full_arrangement(); return 0; }

 

測試結(jié)果：

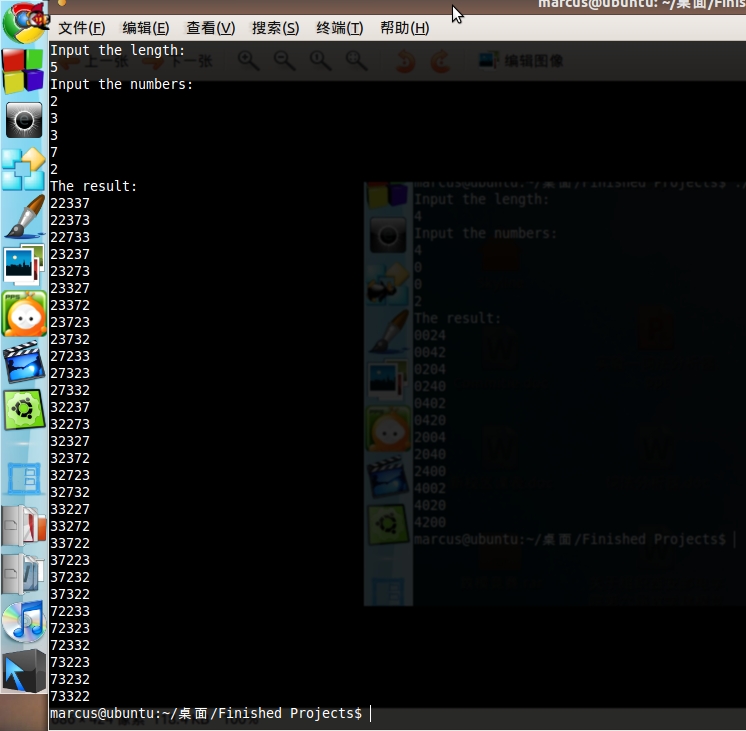
輸入為4002時：

輸入為23372時：

 

輸入為1736542時(部分輸出)：

 

算法分析：

算法中長度為n的子數(shù)列中next_arrangement的調(diào)用次數(shù)的遞推公式A(n)=n*[A(n-1)+A(n-2)+...+A(2)]+1。A(2)=1(n>2)。total(n)=A(n)+A(n-1)+...+A(2)。total(n)也即為空間復(fù)雜度。這個是小于n！的。結(jié)果還在研究。。。

算法中主要的工作是復(fù)制數(shù)組和提前數(shù)字，平均提前的幅度是n/2（姑且這么搞哇。。。）。那么時間復(fù)雜度就是(3/2)*n*total(n)。