請?jiān)趯W(xué)習(xí)完初識二次函數(shù)后再來學(xué)習(xí)。

觀前提示：本章會不定期增補(bǔ)修改。

對\(a,b,c\)的理解

前面已經(jīng)說過，\(a\)決定的是開口方向和大小。

---

那\(b\)呢？

根據(jù)頂點(diǎn)\(V\)的橫坐標(biāo)\(-\frac b {2a}\)可知，如果\(a,b\)異號，則頂點(diǎn)橫坐標(biāo)為正；同號則為負(fù)。

你可能認(rèn)為這沒有什么用，但請務(wù)必記住。在后面的題目中，你會見識到這一點(diǎn)的重要性。

---

\(c\)就比較簡單了，其表示的是拋物線與\(y\)軸交點(diǎn)的縱坐標(biāo)（進(jìn)階一點(diǎn)來說就是在\(y\)軸上的截距）。

待定系數(shù)法確定二次函數(shù)

主播主播你怎么只知道抄你的反比例函數(shù)

別問，問就是懶得重想標(biāo)題了

來看一道期末真題。

（\(2023\)·鼓樓）求下列二次函數(shù)的表達(dá)式：

\((1)\)已知二次函數(shù)圖像經(jīng)過點(diǎn)\((3,0)\)，\((-2,0)\)和\((0,6)\)。
\((2)\)已知二次函數(shù)圖像頂點(diǎn)為\((2,0)\)且經(jīng)過\((-2, 4)\)。

第一題還是比較簡單的，照著一次函數(shù)和反比例函數(shù)來：

解：設(shè)二次函數(shù)表達(dá)式為\(y=ax^2+bx+c(a\neq 0)\)。

由題意得：

\[\left\{ \begin{aligned} &9a+3b+c=0 \\ &4a-2b+c=0\\ &c=6\\ \end{aligned} \right. \]

爆破一手，解得：

\[\left\{ \begin{aligned} &a=-1 \\ &b=1\\ &c=6\\ \end{aligned} \right. \]

\[\therefore 二次函數(shù)表達(dá)式為y=-x^2+x+6 \]

第二題，我先把笨辦法講掉，然后再說簡單的。

解：設(shè)二次函數(shù)表達(dá)式為\(y=ax^2+bx+c(a\neq 0)\)。

由題意得：

\[\left\{ \begin{aligned} &-\frac b {2a}=2 &①\\ &\frac {4ac-b^2} {4a}=0&②\\ &4a-2b+c=4&③\\ \end{aligned} \right. \]

有些同學(xué)不知道怎么解的，我把簡易過程放在這里。

\[②, 4a\ne 0\Rightarrow 4ac-b^2=0\Rightarrow b^2=4ac \]

\[①\Rightarrow b=-4a \]

\[把b=-4a代入②\Rightarrow 16a^2=4ac \]

\[\because a\ne 0\therefore c=4a \]

\[把b=-4a, c=4a代入③\Rightarrow a=\frac 1 4 \]

經(jīng)過代數(shù)爆破，非非非非非非常容易解得：

\[\left\{ \begin{aligned} &a=\frac 1 4 \\ &b=-1\\ &c=1\\ \end{aligned} \right. \]

\[\textcolor{red} {經(jīng)檢驗(yàn)}，二次函數(shù)表達(dá)式為y=\frac 1 4x^2-x+1 \]

想必各位已經(jīng)想到第二種方法了，那就是用頂點(diǎn)式。

解：設(shè)二次函數(shù)表達(dá)式為\(y=a(x+h)^2+k(a\neq 0)\)。

\[\because 頂點(diǎn)坐標(biāo)為(2, 0) \]

\[\therefore h=-2, k=0\Rightarrow y=a(x-2)^2 \]

由題意得：

\[a(-2-2)^2=4 \]

解得：

\[a=\frac 1 4 \]

\[\therefore 二次函數(shù)表達(dá)式為y=\frac 1 4(x-2)^2 \]

你必須承認(rèn)這是本題最簡單的方法了。只要一個一元一次方程，豈不美哉！

你又動起了腦筋。哎，頂點(diǎn)式這么好用，那\((1)\)能不能用啊。

當(dāng)然可以。

解：設(shè)二次函數(shù)表達(dá)式為\(y=a(x+h)^2+k(a\neq 0)\)。

\[\because 函數(shù)圖像過(3, 0), (-2,0) \]

\[\therefore 根據(jù)對稱性，頂點(diǎn)橫坐標(biāo)為\frac {3+(-2)} 2=\frac 1 2 \]

\[\therefore h=-\frac 1 2\Rightarrow y=a(x-\frac 1 2)^2+k \]

由題意得：

\[\left\{ \begin{aligned} &a(3-\frac 1 2)^2+k=0 \\ &a(-\frac 1 2)^2+k=6\\ \end{aligned} \right. \]

（要注意這邊千萬不能再用\((3,0)\)和\((-2, 0)\)了，不然算出來方程組無解的。）

解得：

\[\left\{ \begin {aligned} & a=-1\\ & k=\frac {25} 4\\ \end {aligned} \right. \]

\[\therefore 二次函數(shù)表達(dá)式為y=-(x-\frac 1 2)^2+\frac {25} 4 \]

你必須承認(rèn)這是本題最簡單的方法了。只要一個二元一次方程組，豈不美哉！

不！這不是最簡單的方法！

我 們 要 設(shè) 表 達(dá) 式 為 \(y=a(x-3)(x+2)(a\ne 0)\) 。

由 題 意 得

\[-3\cdot 2a=6 \]

解 得

\[a=-1 \]

\[\therefore y=-(x-3)(x+2)=-x^2+x+6 \]

為什么能這么設(shè)？這是我們要考慮的一個問題。以下內(nèi)容僅做拓展。

都說三點(diǎn)確定一條拋物線（第\((1)\)題的法\(1\)已經(jīng)告訴我們），那如果一條拋物線與\(x\)軸有兩個交點(diǎn)，那就是已經(jīng)確定了拋物線的零點(diǎn)位置。

根據(jù)十字相乘法，能夠因式分解的二次三項(xiàng)式\(x^2+px+q\)，總能分解為\((x+a)(x+b)\)的形式。那為何不直接將二次函數(shù)中的二次三項(xiàng)式寫成十字相乘的形式呢？

需要說明一點(diǎn)，即我們這里的十字相乘不再局限于整數(shù)域（\(\N\)），而擴(kuò)展到了有理數(shù)域。也就是說，分解后的結(jié)果可以是\((x-1145.4514)(x+5418.4188)\)，而“能因式分解”的條件也變?yōu)榱耍?strong>二次三項(xiàng)式等于\(0\)所形成的方程有兩個不等的實(shí)數(shù)根。

目的是因式分解；條件是與\(x\)軸有兩個交點(diǎn)，或者說能夠因式分解。步驟就很簡單了。因式分解后，二次三項(xiàng)式變?yōu)橐粋€多項(xiàng)式乘積的形式。只要任意一個因式為\(0\)，最終值一定為\(0\)。

令二次三項(xiàng)式為\(S\)。根據(jù)試根法，因?yàn)楫?dāng)\(x=3\)時\(S=0\)，因此\(S\)中必含因式\(x-3\)；同理，\(S\)中必含因式\(x+2\)。由于它是二次三項(xiàng)式，不可能有其它含\(x\)的因式，故因式分解后的基本形式確定：\((x+2)(x-3)\)。

當(dāng)你確定基本形式后，你會發(fā)現(xiàn)如果直接將該形式作為二次函數(shù)的運(yùn)算部分，二次項(xiàng)系數(shù)就被固定下來是\(1\)了。況且，你這才兩個點(diǎn)呢。要想控制二次項(xiàng)系數(shù)（或者，從下面的圖中看來，控制開口大小和方向），就加上一個系數(shù)\(a\)。

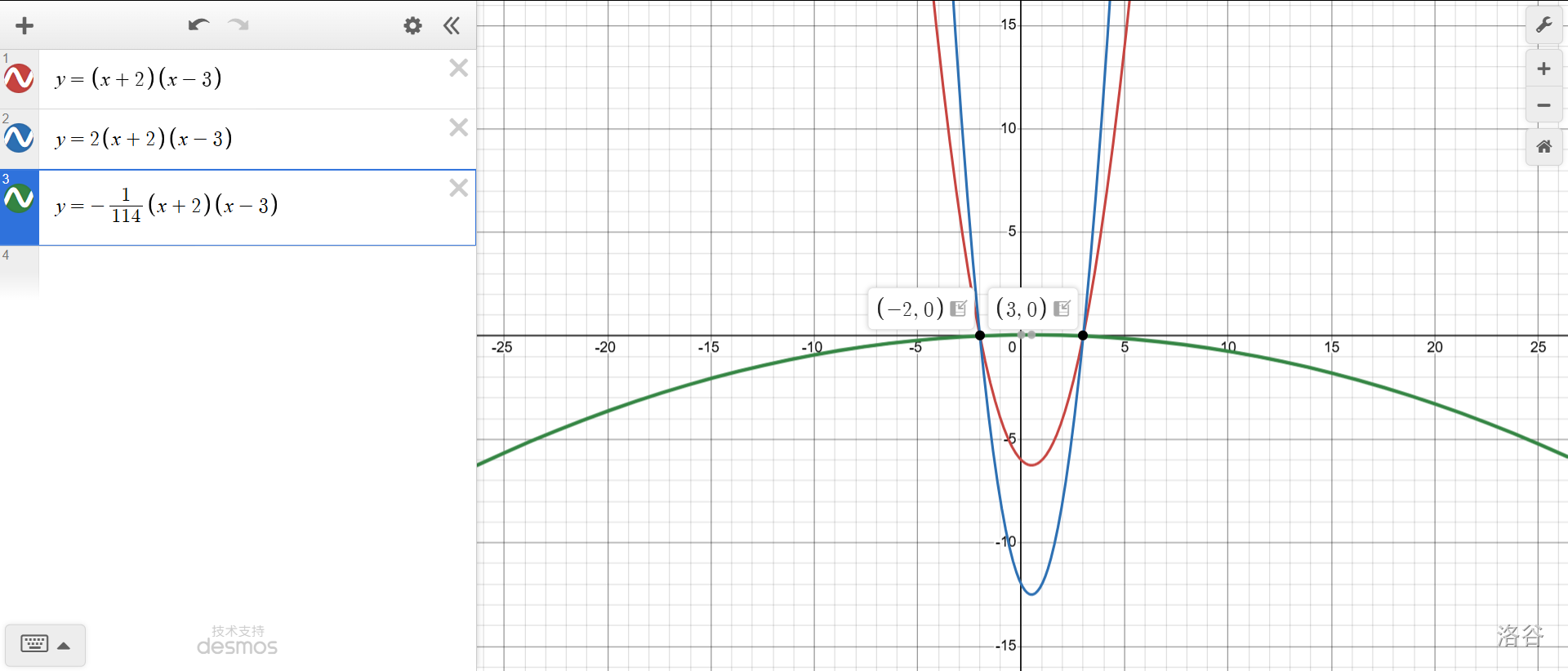
拓展部分到此結(jié)束。如果上面沒聽懂，你只需要記住：

如果已經(jīng)給出一個二次函數(shù)和\(x\)軸有兩個交點(diǎn)，最好是給出其中一個或兩個交點(diǎn)的坐標(biāo)（設(shè)它們分別為\((p, 0)\)，\((q, 0)\)），就可以使用一種課本不承認(rèn)的表示形式：\(y=a(x-p)(x-q)\)。這樣通常可以簡便計(jì)算。

這禁忌之術(shù)就被稱為：

交點(diǎn)式（\(\text {intersection form}\)）。

二次函數(shù)與取值范圍（基礎(chǔ)篇）

對于拋物線\(y=x^2\)，當(dāng)\(-2<x\le-1\)時，\(y\)的取值范圍是多少？

簡單！當(dāng)\(x=-2\)時\(y=4\)；當(dāng)\(x=-1\)時\(y=1\)。取個中間，注意等號，搞定！

好！好啊。那改下題目，看閣下如何應(yīng)對！

對于拋物線\(y=-2x^2\)，當(dāng)\(-3<x<1\)時，\(y\)的取值范圍是多少？

當(dāng)\(x=-3\)時\(y=-18\)；當(dāng)\(x=1\)時\(y=-2\)。取個中間，注意等號，搞定！

住口！你且看看圖像，是如你所言么？

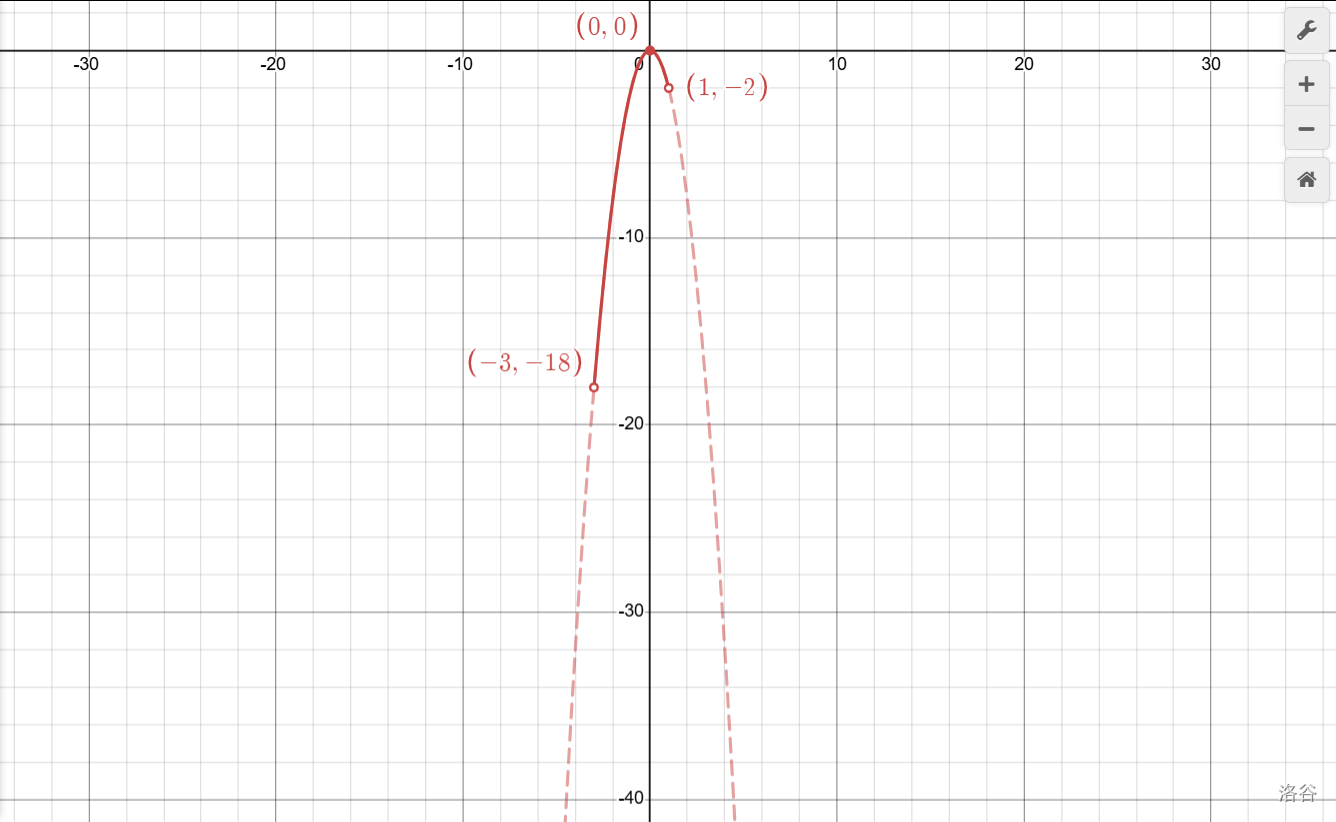
原來，因?yàn)?strong>二次函數(shù)有多個增減性，在頂點(diǎn)處會拐彎，因此要分段考察。做這類題時，應(yīng)遵循如下步驟：

• 看到函數(shù)，先求頂點(diǎn)坐標(biāo)。

  \(y=-2x^2\)，顯然頂點(diǎn)坐標(biāo)\((0,0)\)。

• 看取值范圍是否跨越了頂點(diǎn)。
  • 如果沒跨越，按照許韋升的方法算即可。
  • 如果跨越了，從頂點(diǎn)處劈兩半分別計(jì)算，然后求他們整體覆蓋的取值范圍。

    分成\(-3<x\le 0\)和\(0<x<1\)計(jì)算。

    它們都沒有跨越頂點(diǎn)，因此照常計(jì)算，一個算得\(-18<x\le 0\)，一個算得\(-2<x< 0\)。

    它們兩個合并起來，就是\(-18<x\le 0\)。

當(dāng)然，最保險的方法還是畫圖。主播當(dāng)年錯過這道題，原因就是沒畫圖，然后\(0\)沒取到。

對于下面這一類題目，那還是推薦保險一點(diǎn)的方法。

對于拋物線\(y=-2x^2\)，當(dāng)\(-3<y\le -1\)時，\(x\)的取值范圍是多少？

放心吧，你腦子是轉(zhuǎn)不過來的，老老實(shí)實(shí)畫圖！

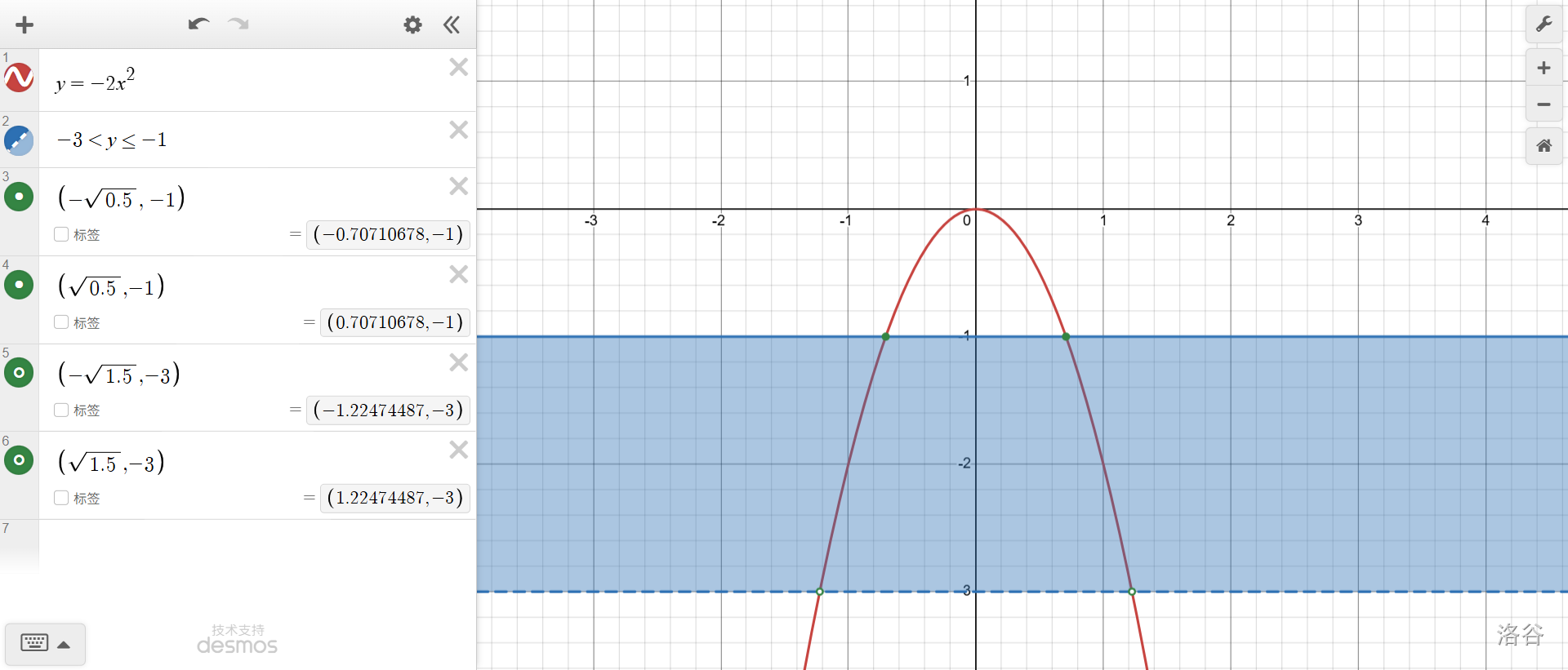
就看被藍(lán)色區(qū)域覆蓋的函數(shù)圖像，竟然還是個分段函數(shù)。\(y=-3\)是虛線，\(y=-1\)是實(shí)線，這個一定要標(biāo)好。四個交點(diǎn)簡單算下：

立馬得到答案\(-\frac {\sqrt 6} 2<x\le -\frac {\sqrt 2} 2\)或\(\frac {\sqrt 2} 2\le x<\frac {\sqrt 6} 2\)。

這類題目主要就是細(xì)心，不能少等號，或者沒取到頂點(diǎn)。想驗(yàn)算？那就畫圖！這種分是不能失的。

畫圖技巧

為什么單獨(dú)劈一塊講“畫圖技巧”呢？

畫一次函數(shù)很簡單，取兩個點(diǎn)（一般是與\(x, y\)軸的交點(diǎn)），尺子一連。
畫反比例函數(shù)也不難，取幾個點(diǎn)（一般是\(k\)的因數(shù)為橫縱坐標(biāo)）大致一連，反正雙曲線長得都差不多。

那拋物線呢？既有開口方向、開口大小的限制，還要確定位置，想畫的相對準(zhǔn)還是比較難的。

對策就是我們之前順嘴提過的一點(diǎn)。

那么如何快速計(jì)算頂點(diǎn)呢？

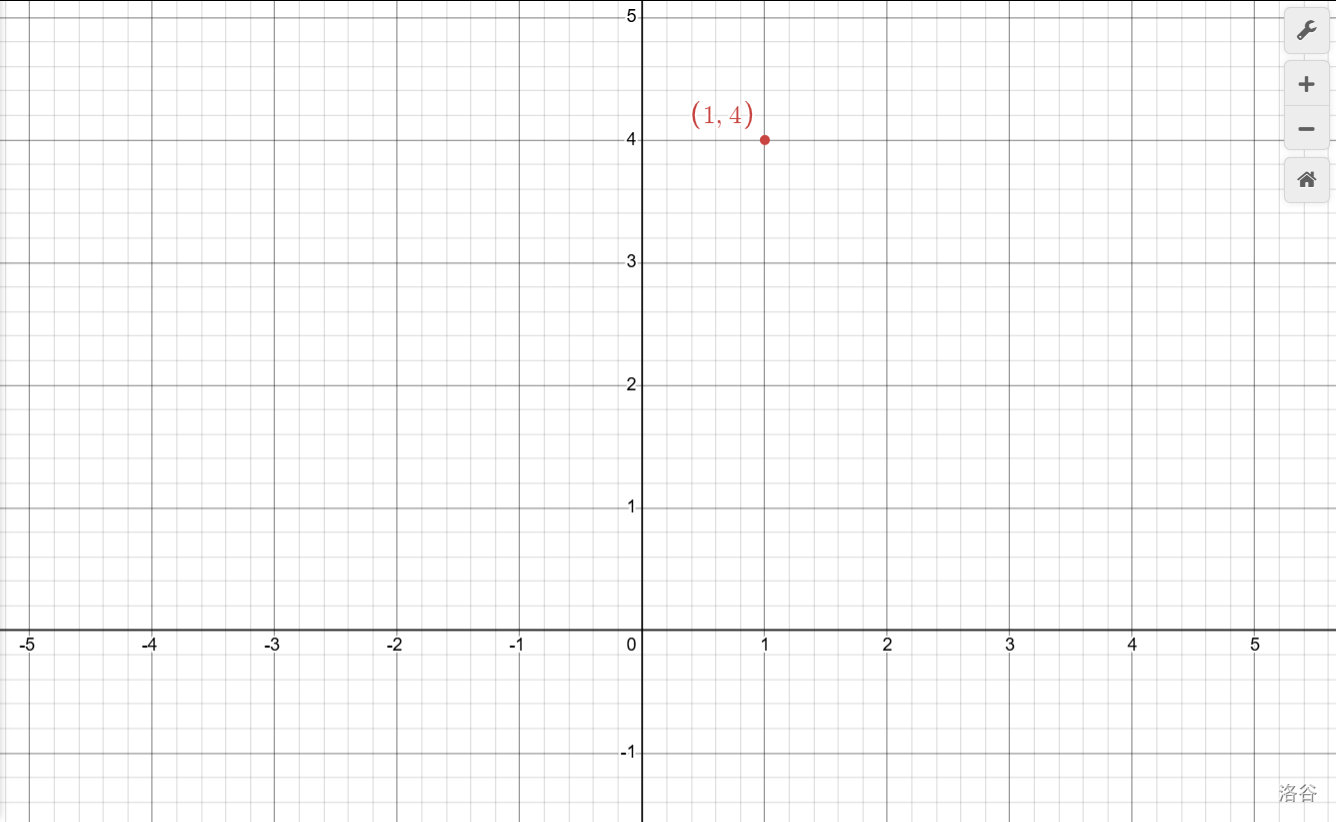
我們都知道頂點(diǎn)坐標(biāo)\((-\frac b {2a}, \frac {4ac-b^2} {4a})\)，但是真的要把\(a,b,c\)代進(jìn)去挨個算嗎？我們體驗(yàn)一下，假設(shè)要計(jì)算\(y=-x^2+2x+3\)的頂點(diǎn)坐標(biāo)。

嗯，先提\(a,b,c\)。

\[a=-1, b=2, c=3 \]

算橫坐標(biāo)。

\[-\frac b {2a}=-\frac 2 {2\times (-1)}=-\frac 2 {-2}=1 \]

算縱坐標(biāo)。

\[\frac {4ac-b^2} {4a}=\frac {4\times (-1)\times 3-2^2} {4\times (-1)}=\frac {-16} {-4}=4 \]

哦！頂點(diǎn)坐標(biāo)是\((1, 4)\)。

不僅費(fèi)草稿紙，又費(fèi)腦子，還容易錯。看到那么長一個分式，你還想算嗎？因此接下來給一個快速算頂點(diǎn)的方法。

第一步還是先提\(a,b,c\)。

\[a=-1, b=2, c=3 \]

觀察到\(a,b\)異號，反過來橫坐標(biāo)為正。

符號不用管了，直接數(shù)值除以兩倍數(shù)值，\(2\)除以\(2\)倍\(1\)，頂點(diǎn)橫坐標(biāo)是\(+1\)。

下一步算縱坐標(biāo)。\(2B\)才把\(\frac {4ac-b^2} {4a}\)代入呢！我直接

\[當(dāng)x=1時，y=-1^2+2+3=4 \]

哦！頂點(diǎn)坐標(biāo)是\((1,4)\)。

確定頂點(diǎn)后，先點(diǎn)出來，大致位置即確定。

然后看\(a=-1\)，說明開口朝下，大小和\(y=x^2\)一樣，就可以動筆了。

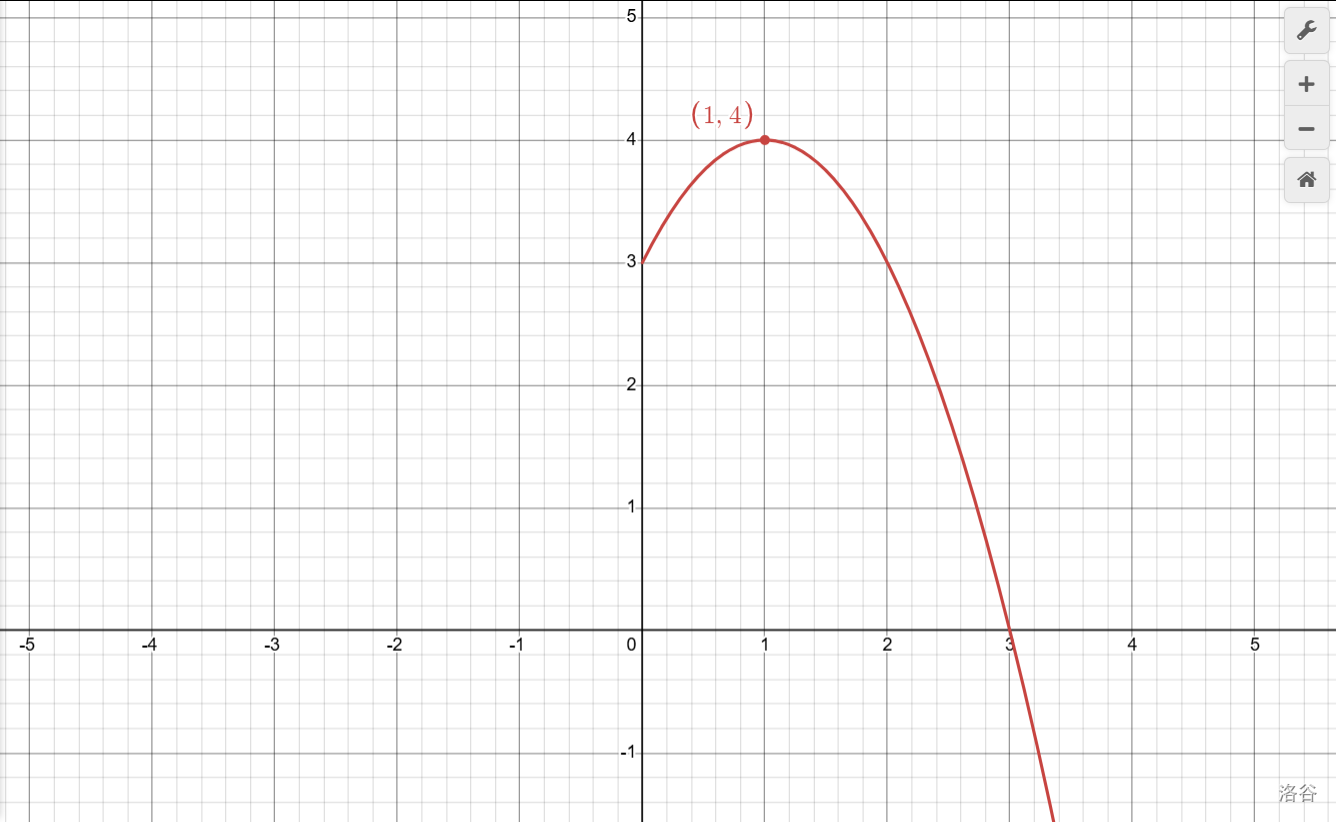
最后可以再看一點(diǎn)，就是和\(y\)軸的交點(diǎn)為\((0,3)\)。拋物線往上懟，然后一路降下去。

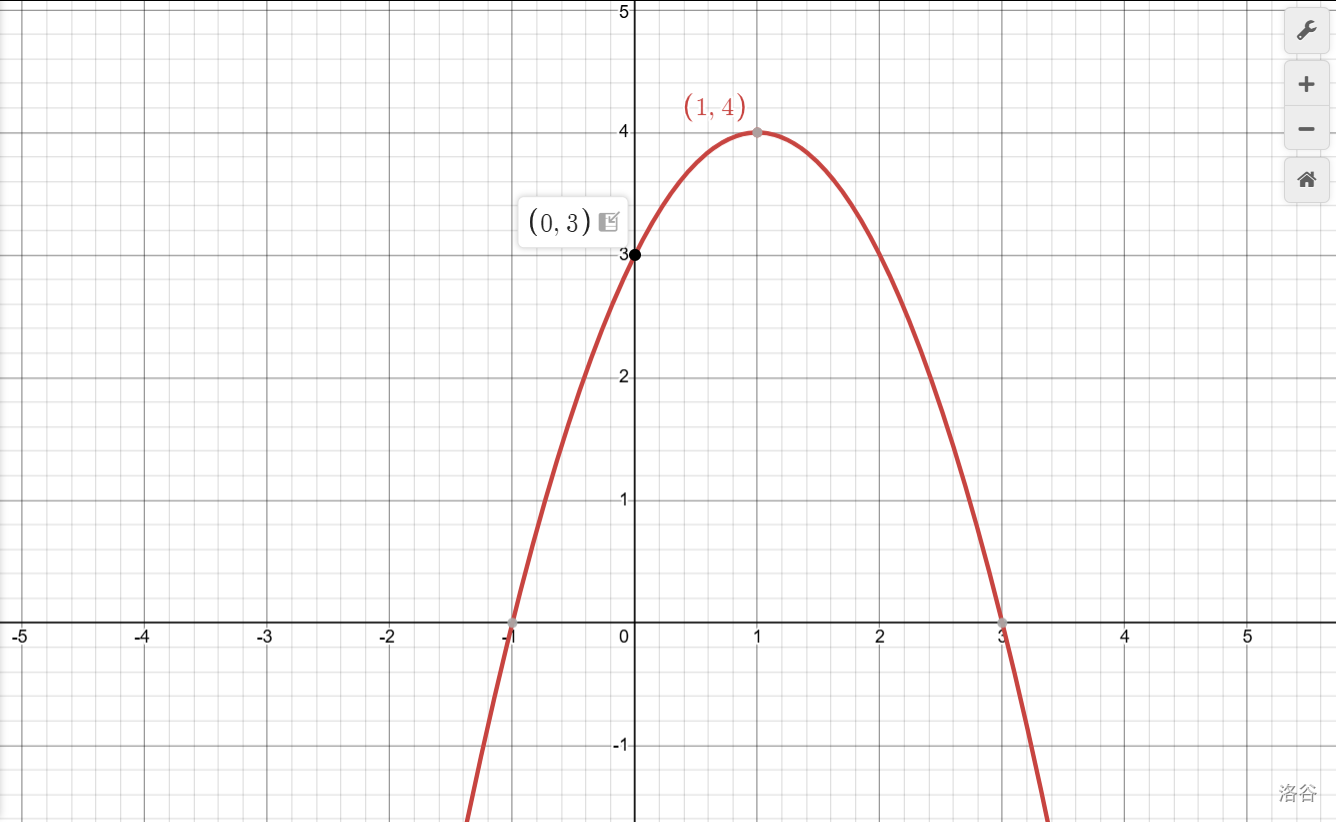
這樣畫出的圖像大致準(zhǔn)了，研究問題時就不會遇到精確度上的問題。

二次函數(shù)與取值范圍（提高篇）

閱讀下面的材料。

小明在學(xué)習(xí)中遇到這樣一個問題：求二次函數(shù)\(y=x^2-6x+7(1\le x\le m)\)的最大值。他畫圖研究后發(fā)現(xiàn)，\(x=1\)和\(x=5\)時的函數(shù)值相等，于是他認(rèn)為需要對\(m\)分類討論。

他的解答過程如下：

\[\because y=x^2-6x+7的對稱軸為直線x=3 \]

\[\therefore x=1和x=5時的函數(shù)值相等 \]

\[若1\le m< 5，則x=1時，y_{max}=2 \]

\[若m\ge 5，則x=m時，y_{max}=m^2-6m+7 \]

請你參考小明的思路，解答下列問題：

\((1)y=2x^2+4x+1(-2\le x\le 4)\)的最大值為\(\_\_\_\)。
\((2)\)求\(y=2x^2+4x+1(p\le x\le 2)\)的最大值。
\((3)\)若\(y=2x^2+4x+1(t\le x\le t+2)\)的最大值為\(31\)，則\(t\)的值為\(\_\_\_\)。

在下面的文字中，我先從高中借一點(diǎn)符號，規(guī)定\(f(a)\)表示\(x=a\)時的函數(shù)值。其實(shí)就是因?yàn)椴幌雽懩敲炊嘧至恕?/p>

第\((1)\)題很簡單，代入基礎(chǔ)篇的技巧即可。

\((2)\)題你一看，跟小明的例題沒有區(qū)別。那我們就先仿它一手，接下來再慢慢講原理。

解：$$\because y=2x^2+4x+1的對稱軸為直線x=-1$$

\[\therefore x=2和x=-4時的函數(shù)值相等 \]

\[若-4< p\le 2，則x=2時，y_{max}=17 \]

\[若m\le -4，則x=p時，y_{max}=2p^2+4p+1 \]

看來光模仿還模仿不來，像這些\(p\)的取值范圍，不搞懂是根本改不過來的。話不多說，先畫圖。

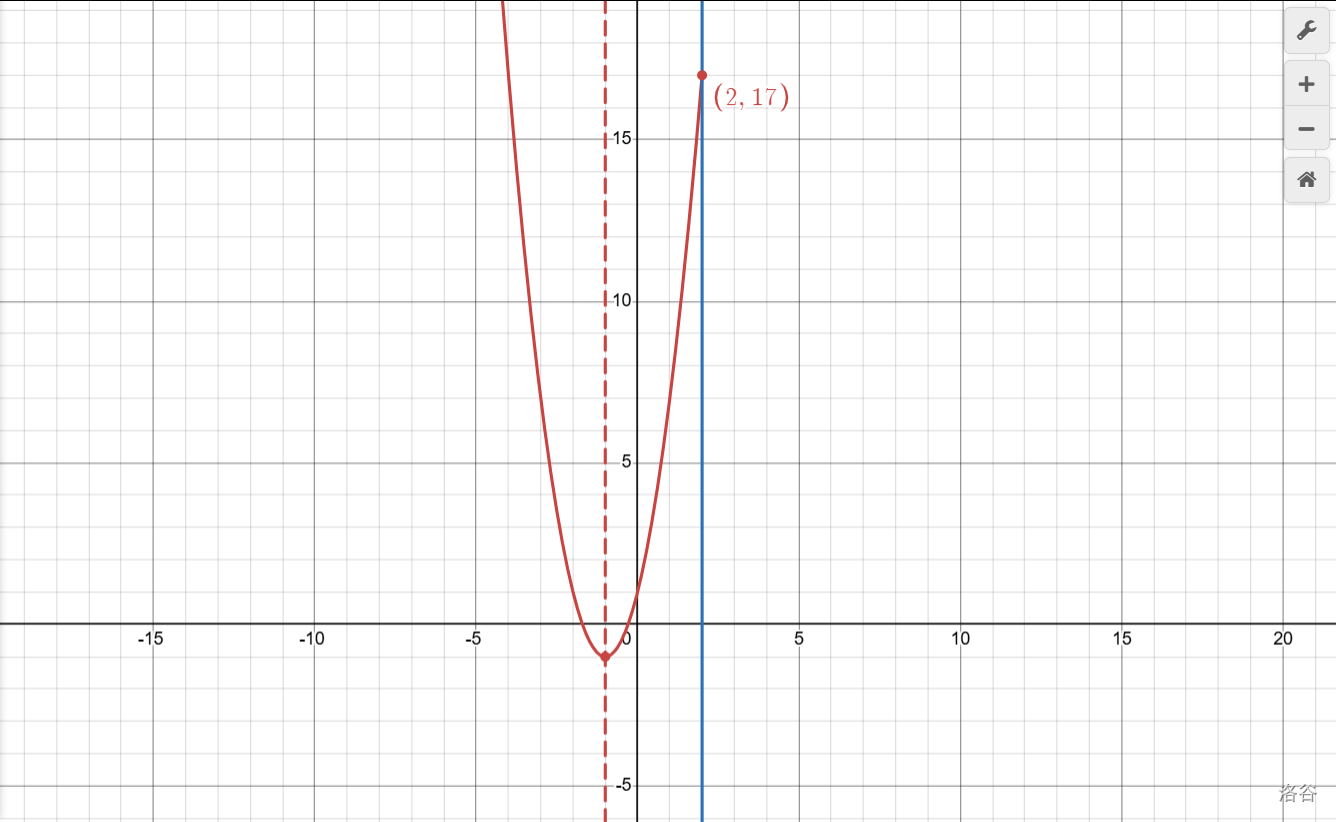
首先可以肯定的是，通過\(p\le x\le 2\)可以看出\(p\le 2\)。那我們就把\(p\)從\(2\)開始，往小的移動，看取值范圍怎么變化。

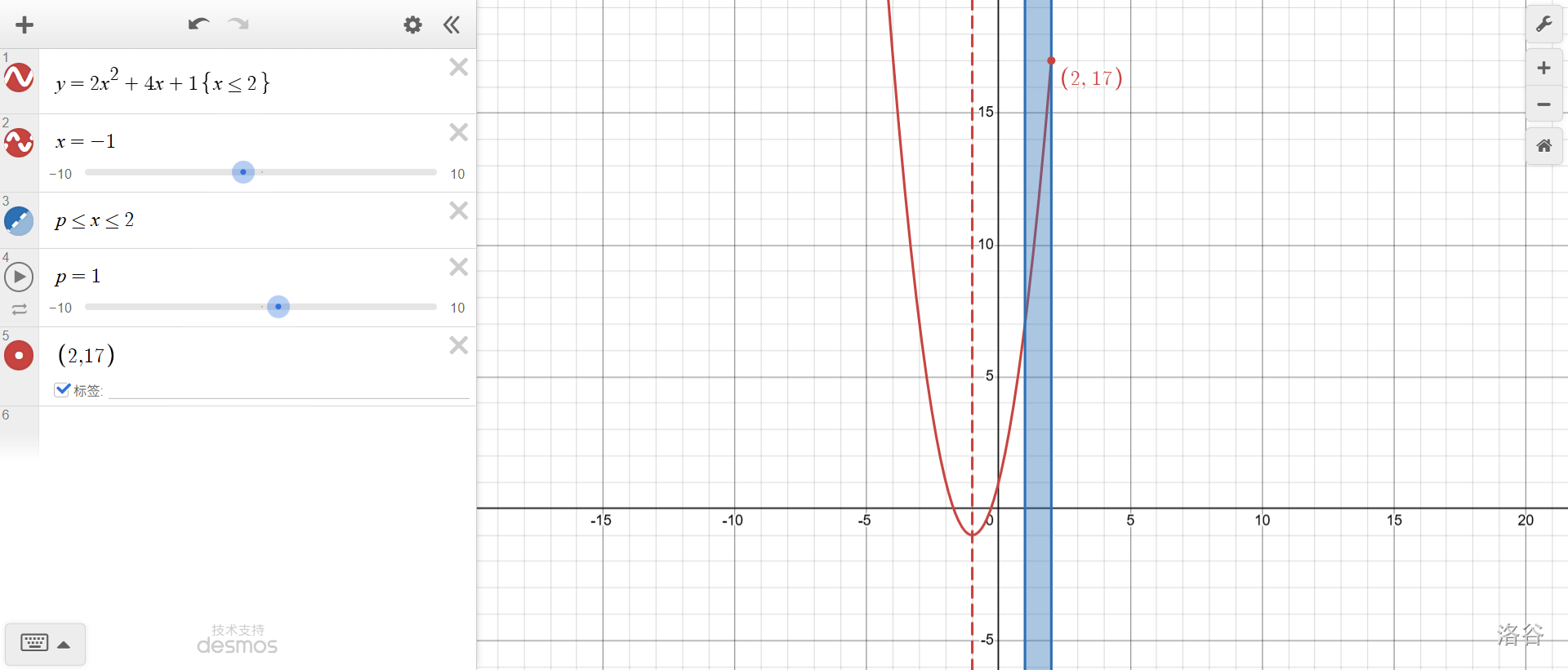
上面是\(p=1\)時。仔細(xì)看藍(lán)色區(qū)域里的圖像，單調(diào)遞增，因此最大值是\(x=2\)時的函數(shù)值，即\(f(2)\)。

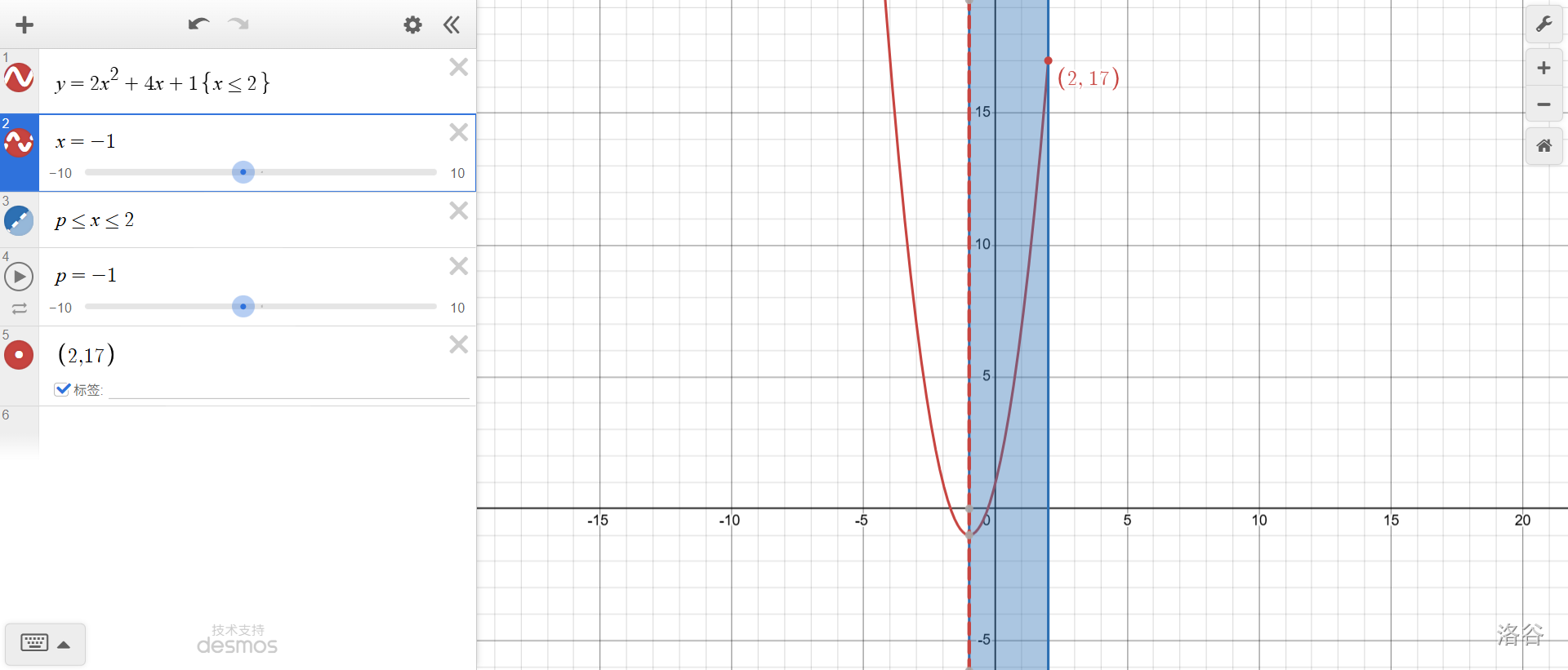
\(p=-1\)了，最大值還是\(f(2)\)。

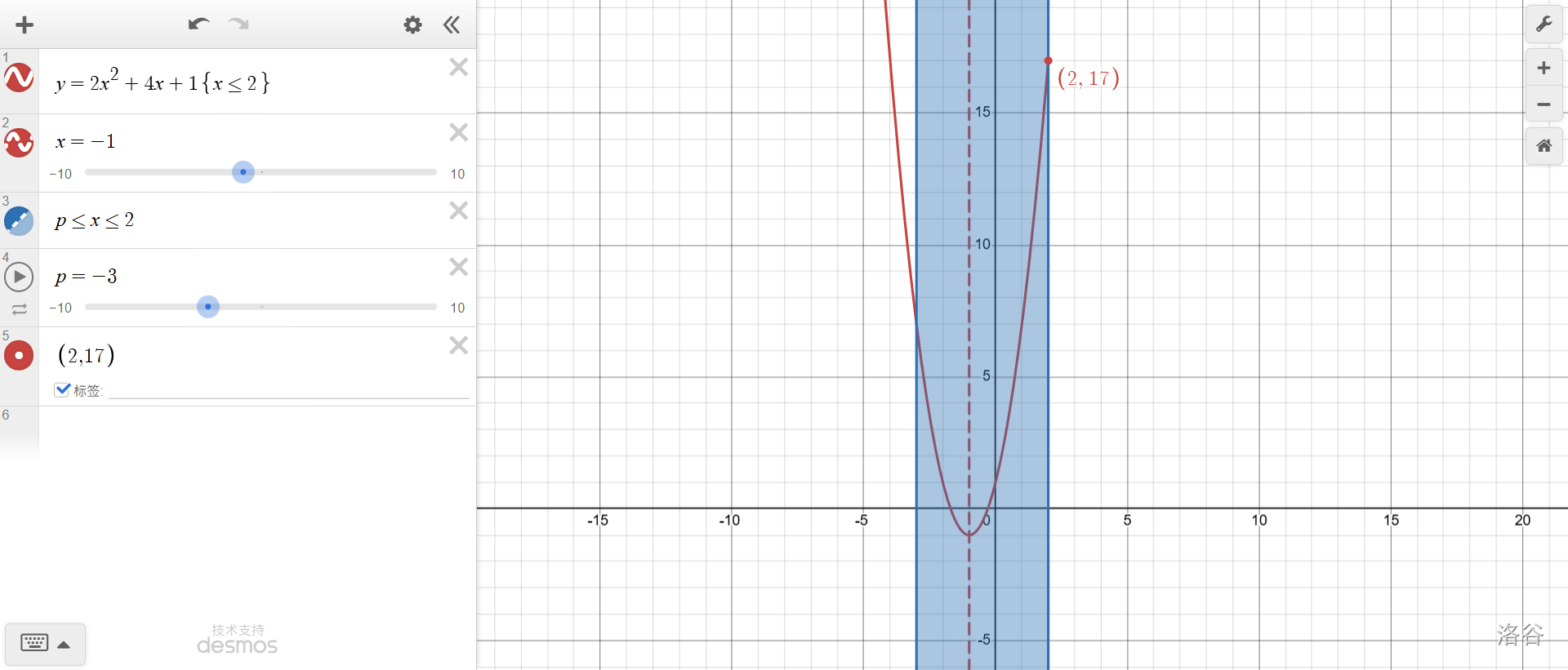
\(p=-3\)，已經(jīng)跨越了頂點(diǎn)，于是劈成兩半。左半邊最大值\(f(-3)\)，右半邊最大值\(f(2)\)。\(f(2)>f(-3)\)，所以最大值依舊是\(f(2)\)。

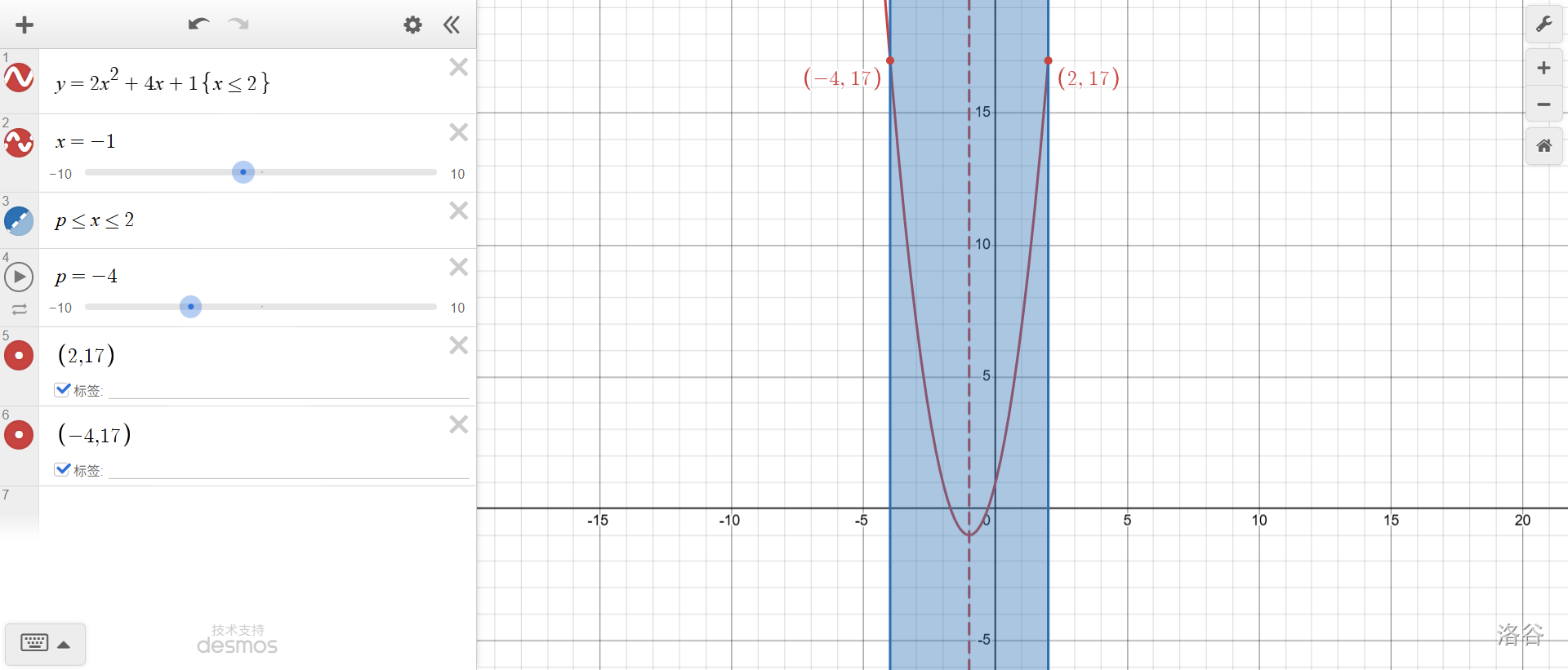
\(p=-4\)時，\(f(2)=f(-4)\)，這也是題目中把該點(diǎn)作為轉(zhuǎn)折點(diǎn)的原因。這一點(diǎn)以后，\(f(2)<f(p)\)了，因此最大值變成\(f(p)\)，并且一直繼續(xù)下去（這是由于\(x<-1\)時，\(y\)隨\(x\)的減小而增大，對于\(p<-4\)，\(f(p)>f(-4)=f(2)\)）。

---

懂得這種“拖進(jìn)度條式”的分析方法后，第\((3)\)題也可以秒解了。\(t\le x\le t+2\)，翻譯一下就是寬度為\(2\)的“進(jìn)度條”在函數(shù)上來回拖動，在某個時候，條內(nèi)函數(shù)的最大值是\(31\)，求這個時候進(jìn)度條拖到哪兒了。

那我們就拽拽看！

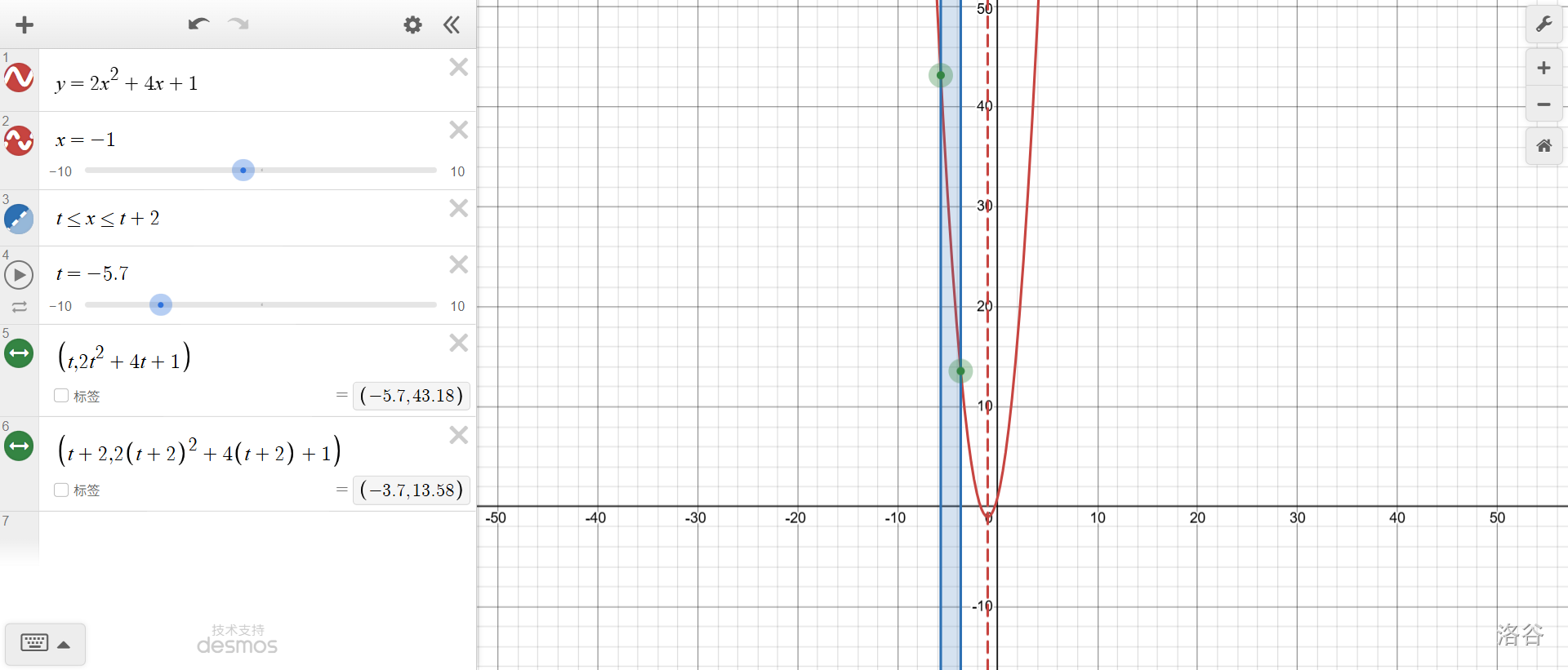
先從\(t+2\le-1\)（進(jìn)度條全部在對稱軸左側(cè)）開始。此時，容易看出，最大值為\(f(t)\)。

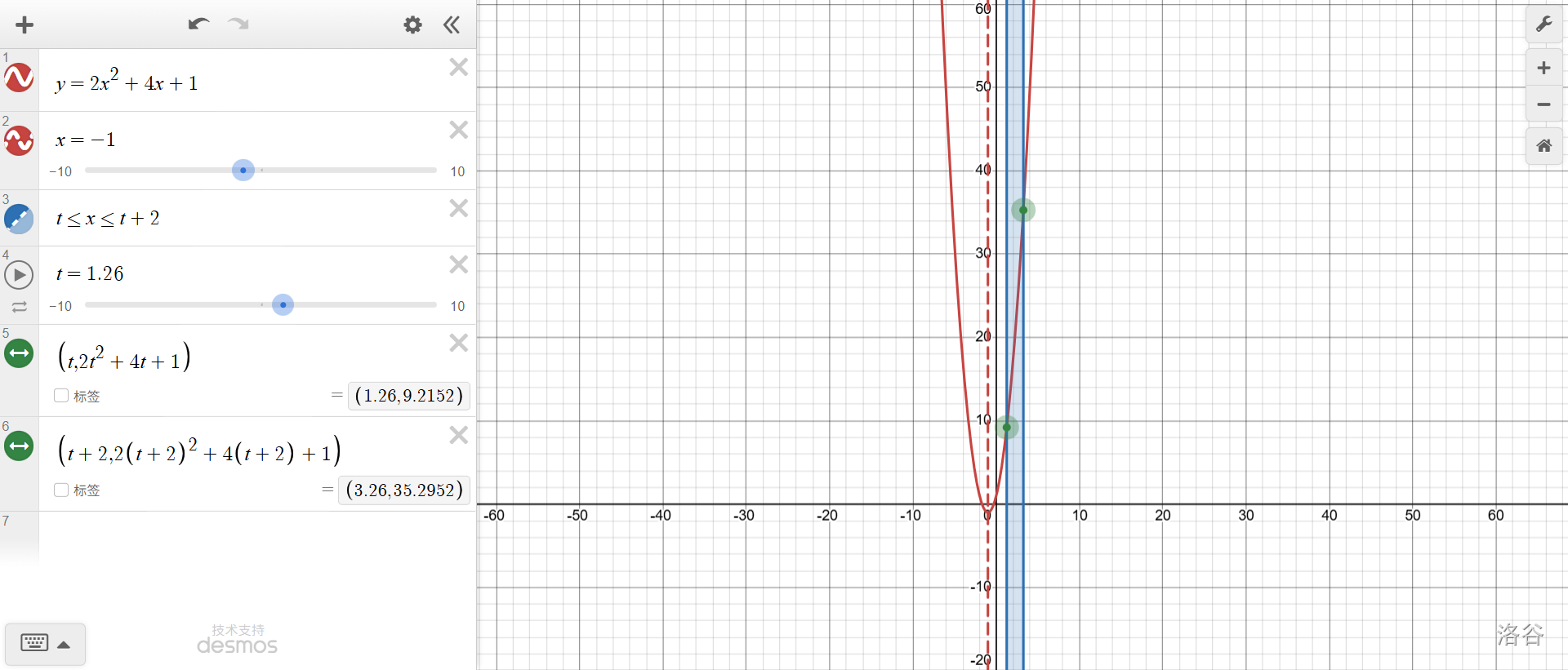
對稱著說，當(dāng)\(t\ge -1\)（全部在對稱軸右側(cè)）時，最大值為\(f(t+2)\)。

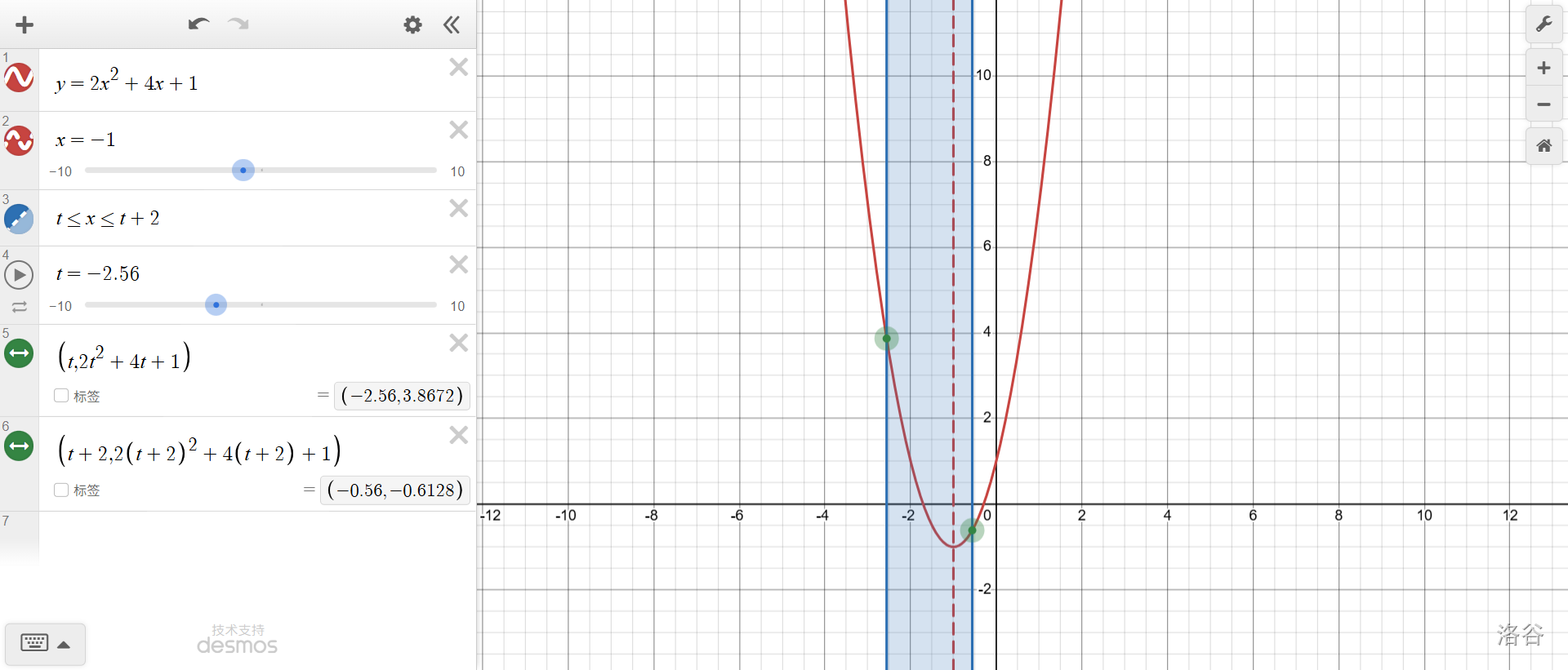
接下來是跨越對稱軸的一部分。上面展示的情況下，\(y_{max}=f(t)\)，但并非總是如此。對稱軸兩側(cè)增減性不同，隨著進(jìn)度條向右拖動（\(x↑\)），一側(cè)下降，一側(cè)上升。由此推斷必定有一個轉(zhuǎn)折點(diǎn)，滿足通過該點(diǎn)之后，\(f(t+2)>f(t)\)，從而最大值變?yōu)?span id="w0obha2h00" class="math inline">\(f(t+2)\)。

再聯(lián)系對稱性，可以知道，轉(zhuǎn)折點(diǎn)（即\(f(t)=f(t+2)\)時）肯定是對稱軸處于\(t\)和\(t+2\)正中間，即\(t+1=-1, t=-2\)的時候。

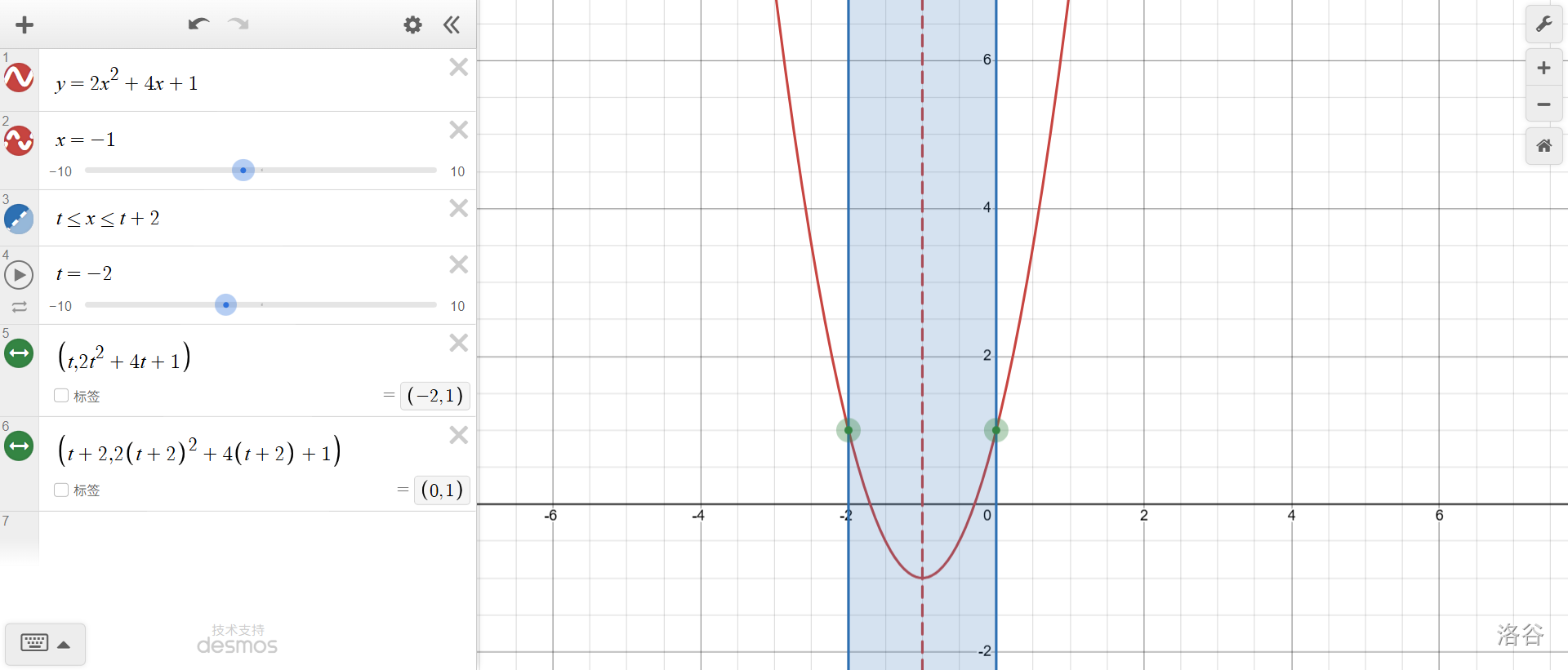
不知道你有沒有發(fā)現(xiàn)，\(y_{max}\)和\(t\)之間，其實(shí)也是一種函數(shù)關(guān)系！根據(jù)我們發(fā)現(xiàn)的結(jié)論，表達(dá)式如下：

還是分段函數(shù)。整理得：

我們要求\(y_{max}=31\)時\(t\)的值。現(xiàn)在目標(biāo)明確，接下來不用多說了吧。

當(dāng)\(y_{max}=31\)時，

\(①t<-2\)：

\[2t^2+4t+1=31 \]

\[解得t_1=3, t_2=-5 \]

其中，\(t_1=3\)不在范圍內(nèi)，舍去。

\(②t\ge-2\)：

\[2(t+2)^2+4(t+2)+1=31 \]

你猜我為什么不化完！

\[t_1+2=3, t_2+2=-5 \]

\[解得t_1=1, t_2=-7 \]

其中，\(t_2=-7\)不在范圍內(nèi)，舍去。

\[\therefore t的值為-5或1. \]

總結(jié)一下，取值范圍類型的題目一般不太難，但前提是你畫圖分析！當(dāng)技巧行不通時，永遠(yuǎn)記住畫圖是你最萬能的法寶。

另外，如果是只有一個不等式的取值范圍，如\(x<-2\)之類，也可以靠畫圖解決。事實(shí)上，它大概率只能靠畫圖解決。

二次函數(shù)中的函數(shù)思想（含參）

你發(fā)現(xiàn)這個標(biāo)題看不懂，于是你繼續(xù)往下讀。

（\(2017\)南京中考改編）已知函數(shù)\(y=-x^2+(m-1)x+m\)（\(m\)為常數(shù)）。

\((1)\)求證：不論\(m\)為何值，該函數(shù)的頂點(diǎn)都在函數(shù)\(y=(x+1)^2\)的圖像上。
\((2)\)當(dāng)\(-2≤m≤3\)時，求該函數(shù)的圖象的頂點(diǎn)縱坐標(biāo)的取值范圍。

你可能認(rèn)為這個題目很簡單，但無論如何還是先分析完。

\((1)\)，證明嘛，按照他的思路，先把頂點(diǎn)表示出來。

提醒一下，之前的技巧在解答題里不能直接用！

接下來，題目轉(zhuǎn)化為：

求證不論\(m\)為何值，點(diǎn)\((\frac {m-1} 2, \frac {(m+1)^2}4)\)都在函數(shù)\(y=(x+1)^2\)的圖像上。

基本功了吧！判斷一個點(diǎn)在不在圖像上，就要把橫坐標(biāo)代入，看縱坐標(biāo)一不一樣。

你暗想這道題也沒什么難度嘛，于是繼續(xù)下一題。

\((2)\)有點(diǎn)繞吧，但是也沒有難到那種程度。要頂點(diǎn)縱坐標(biāo)的取值范圍，無非就是把頂點(diǎn)縱坐標(biāo)用\(m\)表示出來嘛。

到這里你應(yīng)該知道了，\(y_V\)和\(m\)之間又套了一層函數(shù)關(guān)系，這就是這一節(jié)標(biāo)題的意義。

題目轉(zhuǎn)化為：

當(dāng)\(-2≤m≤3\)時，求函數(shù)\(y_V=\frac {(m+1)^2}4\)取值范圍。

取值技巧，啟動！經(jīng)過畫圖和計(jì)算，得到答案：

你又在暗想，這“函數(shù)思想”也沒強(qiáng)到哪里去嘛！還不是輕輕松松就秒掉了。別急，好戲當(dāng)然得在后面啊。

（\(2018\)南京改編）已知二次函數(shù)\(y=2(x-1)(x-m-3)\)（\(m\)為常數(shù)）。當(dāng)\(m\)取什么值時，該函數(shù)的圖像與\(y\)軸的交點(diǎn)在\(x\)軸上方？

太簡單了吧！照他所說，就把二次函數(shù)和\(y\)軸的交點(diǎn)坐標(biāo)表示出來唄！

在\(x\)軸上方，也就是

你還沉浸在秒殺題目的喜悅之中。下面再來一題。

\((1)\)若實(shí)數(shù)\(a,b\)滿足\(a+b^2=2b+1\)，則代數(shù)式\(a^2-4a+2b^2-4b-4\)的最小值為\(\_\_\_\)。
\((2)\)已知實(shí)數(shù)\(a,b\)滿足\(a-b^2=4\)，則代數(shù)式\(a^2-3b^2+a-14\)的最小值為\(\_\_\_\)。

嗯……兩題都是兩個未知數(shù)，讓求最小值，不太現(xiàn)實(shí)。于是你立刻定下目標(biāo)：消元！

先看第\((1)\)題，不知道用誰表示誰，就先看后面要求的代數(shù)式。不難發(fā)現(xiàn)，\(2b^2-4b\)和\(b^2-2b\)有聯(lián)系，那就用\(a\)表示\(b^2-2b\)，得：

代入原式，得：

就是求它最小值！干它！配方結(jié)束戰(zhàn)斗！

還是那句話，趁熱打鐵，來看第\((2)\)題。一眼就是用\(a\)表示\(b^2\)。

代入原式，得：

全錯。怎么樣？驚不驚喜？意不意外？

別急，馬上告訴你錯哪兒了。

你是不是把代入完的代數(shù)式看成了一個函數(shù)？

看嘛，自變量是\(a\)，函數(shù)值就是這個代數(shù)式的值！

那既然是函數(shù)，自變量的取值范圍呢？

先說第\((2)\)題，\(b^2\ge 0\)，那\(a\ge 4\)是必須的吧？

既然\(-3\)取不到，就應(yīng)該另做考慮。簡單驗(yàn)一下增減性，發(fā)現(xiàn)\(f(4)\)（即\(6\)）才是最小值。

第\((1)\)題雖然沒有明顯的范圍提示，但是看見化出的\(b^2-2b=1-a\)就應(yīng)該警惕。\(b^2-2b\)沒有取值范圍嗎？有的。

那么，剛剛配方得到的結(jié)果\((a-3)^2-11\)中，\(a=3\)就是取不到的，函數(shù)的取值范圍限定在\(a\le 2\)。

題目于是轉(zhuǎn)化為：

求\(y=(a-3)^2-11(a\le 2)\)的最小值。

用取值范圍的技巧求得\(y\ge -10\)即可。

這樣看來，函數(shù)思想還不容小覷，尤其是對于套了一層函數(shù)的，尤其要注意自變量的取值范圍。這類范圍一般隱蔽在條件中，如上兩題換元時遇到的平方，難以發(fā)現(xiàn)。如果不把換完的代數(shù)式看成函數(shù)的話，就更想不到取值范圍一回事了。

二次函數(shù)與方程（基礎(chǔ)篇）

結(jié)論其實(shí)和你們預(yù)料的一樣，先奉上。

一般地，二次函數(shù)\(y=ax^2+bx+c\)的圖像與一元二次方程\(ax^2+bx+c=0\)的根有如下關(guān)系：

• 如果二次函數(shù)的圖像與\(x\)軸有兩個交點(diǎn)\((m,0)\)和\((n,0)\)，那么方程有兩個不相等的實(shí)數(shù)根\(x_1=m, x_2=n\)。
• 如果二次函數(shù)的圖像與\(x\)軸只有一個交點(diǎn)\((m, 0)\)，那么方程有兩個相等的實(shí)數(shù)根\(x_1=x_2=m\)。
• 如果二次函數(shù)的圖像與\(x\)軸沒有交點(diǎn)，那么方程無實(shí)數(shù)根。

反之，根據(jù)一元二次方程根的情況，可以判斷對應(yīng)二次函數(shù)的圖像與\(x\)軸的位置關(guān)系。

其實(shí)這一段話的本質(zhì)是“交點(diǎn)\(?\)聯(lián)立方程組”。不信的話，可以梳理一下我們學(xué)過的坐標(biāo)系交點(diǎn)問題，看一看本質(zhì)是不是都是聯(lián)立。

求直線和坐標(biāo)軸的交點(diǎn)：

\[\left\{ \begin{aligned} &y=kx+b\\ &x(\text {or } y)=0\\ \end {aligned} \right. \]

求直線和直線的交點(diǎn)：

\[\left\{ \begin{aligned} &y=k_1x+b_1\\ &y=k_2x+b_2\\ \end {aligned} \right. \]

求直線和反比例函數(shù)圖像的交點(diǎn)：

\[\left\{ \begin{aligned} &y=k_1x+b\\ &y=\frac {k_2}x\\ \end {aligned} \right. \]

（任意兩個反比例函數(shù)圖像之間都沒有交點(diǎn)，且它們和坐標(biāo)軸也沒有交點(diǎn)。）

求拋物線和坐標(biāo)軸的交點(diǎn)：

\[\left\{ \begin{aligned} &y=ax^2+bx+c\\ &x(\text {or } y)=0\\ \end {aligned} \right. \]

甚至還可以有：

求坐標(biāo)軸和坐標(biāo)軸的交點(diǎn)：（疑似瞎搞）

\[\left\{ \begin{aligned} &x=0\\ &y=0\\ \end {aligned} \right. \]

解得：\(\left\{\begin{aligned}&x=0\\&y=0\\\end {aligned}\right.\)，交點(diǎn)坐標(biāo)為\((0,0)\)。（并非瞎搞）

求拋物線和直線的交點(diǎn)：

\[\left\{ \begin{aligned} &y=ax^2+bx+c\\ &y=kx+d\\ \end {aligned} \right. \]

求拋物線和拋物線的交點(diǎn)：

\[\left\{ \begin{aligned} &y=a_1x^2+b_1x+c_1\\ &y=a_2x^2+b_2x+c_2\\ \end {aligned} \right. \]

然后解方程組，把兩個方程右邊連等，出幾個解就有幾個交點(diǎn)（在沒有特殊取值范圍的前提下），代入求\(y\)，每一個點(diǎn)坐標(biāo)就出來了。

課本規(guī)定，如果是函數(shù)圖像和坐標(biāo)軸交點(diǎn)，要寫成如下形式：

本質(zhì)還是聯(lián)立，不是嗎。但如果寫成方程組應(yīng)該也不會算錯。

同樣的，如果是解方程（組）的問題，有時也可以從“形”的角度看成函數(shù)圖像的交點(diǎn)。這一塊不再細(xì)講，題目走起。

已知二次函數(shù)\(y=kx^2-7x-7\)的圖像與\(x\)軸有兩個交點(diǎn)，求\(k\)的取值范圍。

哎呀太簡單了吧！有兩個交點(diǎn)說明\(b^2-4ac>0\)，代入：

你要真這么答，遇到某些嚴(yán)格的老師，一整題的分就沒嘍。

怎么錯的？那我問你，題目里的二次函數(shù)，加粗了還看不見？\(k\)要滿足什么要求？

你感到不服，心里暗暗叫苦，\(****\)玩意兒，非得陰我，就是不講武德！于是接著看下一題。

已知函數(shù)\(y=mx^2+3mx+m-1\)的圖像與坐標(biāo)軸恰有兩個公共點(diǎn)，則實(shí)數(shù)\(m\)的值為\(\_\_\_\)。

假設(shè)你在考場上，你的思路大概會是這樣的。

嗯，看上去不是難題，一分半秒殺，坐標(biāo)軸恰有兩個交點(diǎn)，說明是\(x,y\)兩軸加起來兩個，\(y\)軸自己肯定有且只有一個，原因很簡單，當(dāng)\(x=0\)時\(y\)肯定有值，那廢話不多說，就是說和\(x\)軸只有\(1\)個交點(diǎn)，Wow這不是我剛背過的方程與函數(shù)關(guān)系嗎，既然是二次函數(shù)，等等，這是二次函數(shù)嗎，這不是，只說了函數(shù)，二次項(xiàng)還有系數(shù)，系數(shù)還沒說不等于\(0\)，哈哈哈發(fā)現(xiàn)坑了，分情況討論，第一種\(m=0\)，變成常函數(shù)\(y=-1\)，和\(x\)軸沒有公共點(diǎn)，排除，第二種\(m\ne 0\)，也就是\(b^2-4ac=0\)，恰好和\(x\)軸只有一個交點(diǎn)，列方程\((3m)^2-4m(m-1)=0\)，趕緊解，說好的一分半馬上要過了，化簡得\(5m^2+4m=0\)，秒得\(m_1=0\)，哎呀不是說\(m\ne 0\)嗎，劃掉，第二個解\(m_2=-\frac 4 5\)，正合我意，填上去，哎呀好險好險。

這就是考場上的頭腦，一逗到底中間不帶停頓的。說實(shí)話能想到函數(shù)分類討論的已經(jīng)很不錯了，可惜后來要排除掉。

不過，這道題還有坑，非常深，我當(dāng)時也是到最后才發(fā)現(xiàn)。

請問，\(y\)軸上的那個交點(diǎn)一定是\(y\)軸的嗎？為什么不能是\(x,y\)軸的公共點(diǎn)呢？

哦，布豪，過原點(diǎn)的沒算上，也就是當(dāng)\(x=0\)時\(y=0\)，得到條件\(m-1=0\Rightarrow m=1\)，驗(yàn)算一手，\(y=x^2+3x\)，過原點(diǎn)，而且交點(diǎn)分別是\((0,0)\)和\((-3,0)\)，完全符合條件，答案是\(-\frac 4 5\)或\(1\)，Perfect！

沒想到吧，如果真的那么罵，不管什么題都是出題老師在背后陰你了。所以說，還是得多考慮一手，說不定\(3\)分就回來了呢。

再下面一題就沒有坑了，我保證！

二次函數(shù)\(y=ax^2+bx+c(a\ne 0)\)的圖像如圖所示。

若方程\(ax^2+bx+c=k\)有兩個不相等的實(shí)數(shù)根，求\(k\)的取值范圍。

我跟你說，遇到這種函數(shù)和方程長得像，但又不是完全一樣的這種情況，就把函數(shù)往方程上湊，或者方程往函數(shù)上湊。對于這道題，轉(zhuǎn)化的方法有兩種。

1. 注意到\(ax^2+bx+c=k\Rightarrow ax^2+bx+c-k=0\)。由此理解為：函數(shù)\(y=ax^2+bx+c\)向下平移\(k\)個單位所得的圖像和\(x\)軸的交點(diǎn)。有兩個不相等的實(shí)數(shù)根，就是說交點(diǎn)有兩個。容易發(fā)現(xiàn)，只要\(k<2\)即可。\(k=2\)的情況你可以看一下，正好只有一個交點(diǎn)，不滿足要求。
2. 注意到\(ax^2+bx+c=k\)可以理解為：函數(shù)\(y=ax^2+bx+c\)和\(y=k\)的交點(diǎn)。有兩個不相等的實(shí)數(shù)根，就是說交點(diǎn)有兩個。容易發(fā)現(xiàn)，只要\(k<2\)即可。\(k=2\)的情況你可以看一下，正好只有一個交點(diǎn)，不滿足要求。

（怎么有一股淡淡的人機(jī)感）你看，本質(zhì)是一樣的。

常見坑匯總

由二次函數(shù)兩半增減性不同引申出如下坑：

• 給出\(x\)的取值范圍時故意跨過頂點(diǎn)。
• 不給你\(x\)的取值范圍，給\(y\)的，這種有時雙答案。
• 不定取值范圍（提高篇例題）時，頂點(diǎn)左右最值可能需要分類討論。

以上坑的共同對策是畫圖。

由換元類題目或函數(shù)思想引申出如下坑：

• 自變量的取值范圍隱藏在另一個自變量里。

對策是把式子看成函數(shù)，仔細(xì)尋找自變量的取值范圍。

由題目文字游戲引申出以下坑：

• “雙圈問題”。
  仿照一元二次方程，這類題目通常在二次函數(shù)和函數(shù)的說法之間切換，把實(shí)數(shù)根的說法換成與\(x\)軸的交點(diǎn)即可。以下是它們的例題對比：

  已知方程\(y=kx^2-7x-7\)有兩個不等的實(shí)數(shù)根，求\(k\)的取值范圍。

  已知二次函數(shù)\(y=kx^2-7x-7\)的圖像與\(x\)軸有兩個交點(diǎn)，求\(k\)的取值范圍。

對策如下：

如果二次項(xiàng)系數(shù)不含參，那放心做，必須是二次函數(shù)。

如果二次項(xiàng)系數(shù)含參，再看第一個圈里的內(nèi)容。

• 第一個圈是二次函數(shù)的話，先寫下二次項(xiàng)系數(shù)不等于\(0\)，以防后面忘掉，然后正常做題，最后帶上這個條件即可。
• 第一個圈是函數(shù)的話，分類討論二次項(xiàng)系數(shù)是不是\(0\)，務(wù)必記住后面要把兩種情況合起來。

二次函數(shù)與方程（提高篇）

——交點(diǎn)、聯(lián)立在大題和壓軸題中的運(yùn)用

先上個有難度的。僅做拓展！

思考：方程\(|x^2-2x-3|=2x+b\)解的個數(shù)。

煮啵做的視頻

管它什么方程，來個硬碰硬看看！

\(①x^2-2x-3> 0\)，即\(x<-1\)或\(x>3\)時：

原方程可化為：

\[x^2-2x-3=2x+b \]

整理，得：

\[x^2-4x-(b+3)=0 \]

這里容我偷個懶，把\(\Delta\)借過來用。

\[\Delta=(-4)^2-4\cdot (-b-3)=4b+28 \]

討論\(\Delta\)和\(0\)的大小關(guān)系。

\(1\degree \Delta>0\)，即\(x>-7\)時，求出兩個實(shí)數(shù)根：

\[x=\frac {-b±\sqrt {\Delta}} {2a}=\frac {4±\sqrt{4b+28}} 2=2±\sqrt {b+7} \]

\[\therefore x_1=2+\sqrt {b+7}, x_2=2-\sqrt {b+7} \]

\[\dots \]

好吧，看到后面還有\(\Delta\)兩種情況，絕對值內(nèi)一種情況，\(x\)和\(b\)的關(guān)系還理不清，是時候換種思路了。

哦？之前好像講過，解方程可以用“形”的方法考慮的來著。把等式左右看成函數(shù)！

畫出圖像。\(y_1\)的圖像有點(diǎn)難畫，不過沒關(guān)系！絕對值得特性我們已經(jīng)探究過了，這里復(fù)習(xí)一下。

對于絕對值函數(shù)\(y=|f(x)|\)（這里的\(f(x)\)指任意的函數(shù)運(yùn)算，因?yàn)槲覀儾⒉恢澜^對值里面是什么，所以統(tǒng)一用\(f(x)\)代替，意思是自變量\(x\)進(jìn)行一次規(guī)定的函數(shù)運(yùn)算。它可以是\(kx+b\)、\(\frac k x\)、\(ax^2+bx+c\)等），可以拆分成一個分段函數(shù)：

\[\left\{ \begin{aligned} &y=f(x)&f(x)\ge 0\\ &y=-f(x)&f(x)<0\\ \end{aligned} \right.\]

容易發(fā)現(xiàn)，其圖像在\(x\)軸上半部分（\(y\ge 0\)）是\(y=f(x)\)的圖像，而剩余部分是\(y=-f(x)\)的圖像。

不難得到，\(y=-f(x)\)的圖像和\(y=f(x)\)關(guān)于\(x\)軸對稱。簡易證明如下：

設(shè)\(y=-f(x)(x<0)\)上有一點(diǎn)\((t, -f(t))\)。

其對稱點(diǎn)\((t, f(t))\)顯然在\(y=f(x)\)圖像上。得證。

代到現(xiàn)在，\(y_1\)的函數(shù)圖像在\(x\)軸上半部分是\(y=x^2-2x-3\)的圖像，而剩余部分則把\(y=x^2-2x-3\)沿\(x\)軸翻折即可，也就是\(y=-x^2+2x+3\)的圖像。（記住！后面要考）

輕松畫出來。\(y_2\)就更簡單了，“移一移”即可。