僅需通曉初二及其前置知識，和一元二次方程即可學習。

引入：從方程到函數

回顧我們學習一次函數的時候，探討了一次函數和一元一次方程的關系，例如一次函數\(y=kx+b(k\neq 0)\)和\(x\)軸交點橫坐標就是方程\(kx+b=0\)的解等等。

那么，我們已經學習了一元二次方程，從一次代數的學習正式跨入了二次。那么，你能否想到一種函數，使其與一元二次方程的關系和一次函數與一元一次方程的關系類似呢？

定義：你猜這塊考什么

形如\(y=ax^2+bx+c(a,b,c為常數, a\neq 0)\)的函數叫作二次函數（\(\text {quadratic function}\)）。

相信同學們一眼就能看出這句話里哪些詞最重要。

• \(y=ax^2+bx+c\)是二次函數的定義式，肯定重要。
• 但是考試經常考的，和一次函數一樣容易錯的，必定是\(a\neq 0\)。

備注：如果函數可以化成二次函數的定義式而且定義域（怎么又說錯了）取值范圍不變的話，其也是二次函數。

這塊有一次函數的一元二次方程的經驗，就不贅述了。

性質探究：從反比例到二次

都知道下一步要做什么吧??

不過，為了降低難度，我決定把定義式\(y=ax^2+bx+c\)先換成特殊情況（\(a=1,b=c=0\)）：\(y=x^2\)。

現在，探究以下問題：

1. 畫出\(y=x^2\)的圖像。
2. 其圖像是一條直線嗎？請說明理由。
3. 增減性如何？請證明。
4. 對稱性如何？請證明。
5. 有最大 / 最小值嗎？是多少？
6. 你覺得圖像里有某個特殊點嗎？

每一個都奇長無比，不過我們還是得證，證完就更容易記住，并且可以由證明過程引申很多。

直線還是曲線？

通過描幾個點，我們很容易發現它們都不在一條直線上。

\(x\)	\(1\)	\(-1\)	\(2\)
\(y\)	\(1\)	\(1\)	\(4\)

但是我們不能以偏概全，要想證明它整體的圖像是個曲線，就要仿照反比例函數。

有三個二次函數上的點前來\(\_\_\)。我們設為\(A(a, a^2)\)，\(B(b, b^2)\)，\(C(c, c^2)\)。不妨設\(a<b<c\)，其實這一步是要排除\(a=b=c\)的情況。

法\(1\)：距離公式爆肝\(AB+BC>AC\)

這種方法我是試過的，你也可以試試。到最后一堆根號化不完，在目前看來這種情況必須舍去。可謂是“試試就逝世”。

法\(2\)：\(k_{AB}\neq k_{BC}\)

這種方法還是和以前一樣好用啊。

\[k_{AB}=\frac {\Delta y}{\Delta x}=\frac {b^2-a^2}{b-a}=\frac {(b+a)(b-a)} {b-a}=b+a \]

（這句要講清因為\(a<b\)才可以把\(b-a\)約掉的。）

\[k_{BC}=\frac {\Delta y}{\Delta x}=\frac {c^2-b^2}{c-b}=\frac {(c+b)(c-b)} {c-b}=c+b \]

（同理。）

\[\because a<c\therefore b+a<c+b \]

\[k_{AB}\neq k_{BC} \]

\[\therefore 圖像上任意三點都不在一條直線上 \]

\[\text {Q.E.D.} \]

注中注：\(\text {Q.E.D.}\)是證明完畢的意思。考試不要用啊！被老師罵了別找我。

接下來給各位引入一種新方法。它比法\(2\)更快，并且可以直接解決一般定義式（\(y=ax^2+bx+c\)）的證明！

法\(3\)：一元二次方程，啟動！

假設有一條直線\(y=kx+d(k\neq 0)\)，滿足二次函數\(y=ax^2+bx+c(a\neq 0)\)上至少三個點在直線上。如果我們找不出這樣的一條直線，則二次函數圖像必定非直線。

聯立。

\[\left\{ \begin{aligned} &y=kx+d \\ &y=ax^2+bx+c\\ \end{aligned} \right. \]

右側連等，我們的目的是找到連等后方程解的個數，根據我們探究出的方程與函數關系，就可以看出直線與二次函數交點的個數。

\[ax^2+bx+c=kx+d \]

注意到是一元二次方程，因此整理：

\[ax^2+(b-k)x+(c-d)=0\ \ \ \ (a\neq 0) \]

這個一元二次方程全是參數，我們無法確定\(b^2-4ac\)的大小，但是我們可以肯定，

這個方程最多只有兩個解。

\[\text {耶！反證法得了MVP！} \]

因此我們只能用平滑的曲線去連接我們描出的點。畫出來以后像物理中的拋物線（參見物理必修二：拋體運動），那就把二次函數的圖像叫作：

拋物線（\(\text {parabola}\)）。

增減性

畫出圖像以后我們就很輕松地看出來了。

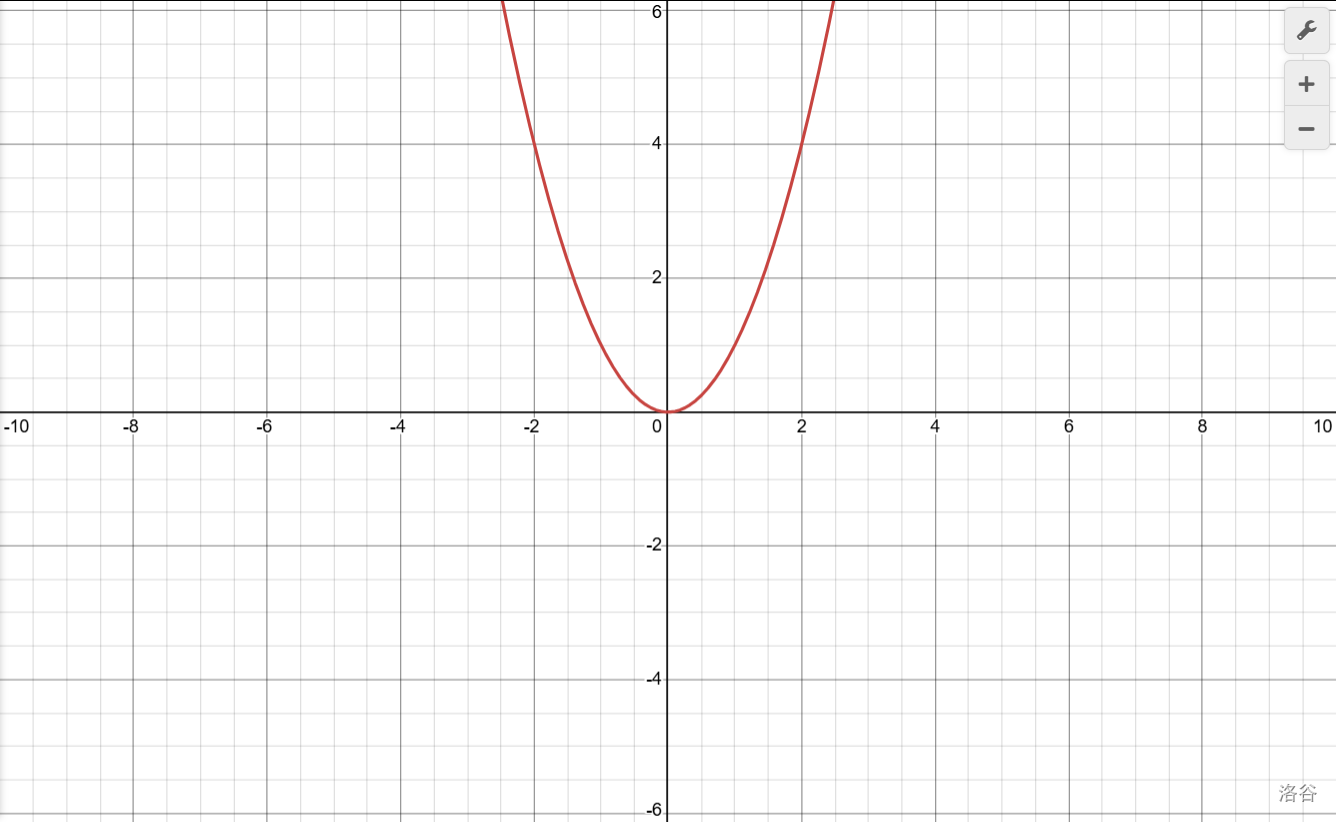
哎呀這不就是當\(x<0\)時\(y\)隨\(x\)增大而減小\(x>0\)時候\(y\)隨\(x\)增大而增大嘛！

上面這句話里有兩個問題。

• 只討論了\(x<0\)和\(x>0\)兩種情況，那\(x=0\)呢？歸誰？
• 證明呢？你說的誰信啊（也就改卷老師不信）。

那我們改一下，把等于\(0\)歸到大于\(0\)里面，順便證明一手。

設拋物線上兩點\(A(a, a^2)\)，\(B(b, b^2)\)，且\(a<b\)。

\(①x<0\)，即\(a<b<0\)：

根據我們之前的思路，我們只要證明\(a^2>b^2\)就行了。

\[\because a^2-b^2=(a+b)(a-b); \]

\[a<0, b<0\Rightarrow a+b<0; \]

\[a<b\Rightarrow a-b<0; \]

\[\therefore (a+b)(a-b)>0 \]

\[\therefore a^2>b^2 \]

\[\text {Q.E.D.} \]

\(②x\geq 0\)，即\(0\leq a<b\)：

同理，只需證\(a^2<b^2\)即可。

\[\because a^2-b^2=(a+b)(a-b); \]

\[a>0, b\geq 0\Rightarrow a+b>0; \]

\[a<b\Rightarrow a-b<0; \]

\[\therefore (a+b)(a-b)<0 \]

\[\therefore a^2<b^2 \]

\[\text {Q.E.D.} \]

對于拋物線\(y=x^2\)：

• 當\(x<0\)時，\(y\)隨\(x\)增大而減小；
• 當\(x\geq 0\)時，\(y\)隨\(x\)增大而增大。

對稱性

借一手之前的圖。

容易看出，拋物線關于\(y\)軸對稱。證明：

設拋物線上一點\(A(a, a^2)\)。

其關于\(y\)軸的對稱點為\(A'(-a, a^2)\)。

\[\because (-a)^2=a^2 \]

\[\therefore 點A'在拋物線上 \]

\[\therefore y=x^2圖像關于y軸對稱 \]

沒有其它對稱軸了。那么，思考所有拋物線都關于\(y\)軸對稱嗎？如果不是，它們的對稱軸分別是哪條直線？

最值（取值范圍）

\[\because x^2\ge 0 \]

\[\therefore 當x=0時，y=x^2有最小值為0 \]

或者可以寫成：

\[對于函數y=x^2，當x=0時，y_{min}=0 \]

這里我們利用平方的非負性解決（記住了！后面要考）。

另外，

• 自變量\(x\)的取值范圍是全體實數；
• 函數\(y\)的取值范圍是\(y\geq 0\)。

特殊點

如果你現在仍然判斷不出來哪個點是特殊點，請按照以下思路思考：

• 一次函數中\(y\)有最值嗎？
• 反比例函數中\(y\)有最值嗎？
• 二次函數中\(y\)有最值嗎？有，那最值點是哪一點？

我們剛剛說當\(x=0\)時\(y_{min}=0\)，因此該最小值對應圖像上的一個點，即\((0, 0)\)。

我們看看該點包含了哪些信息。

• 有了這個點你可以大致確定拋物線的位置。
• 該點左側\(y\)隨\(x\)增大而減小，右側相反。
• 該點通過的垂直于\(x\)軸的直線是拋物線的對稱軸。
• 該點是最值點，在\(y=x^2\)中是最小值。
• ……

可以看出這個點很重要。我們把它稱為頂點（\(\text {vertex}\)）。

從圖像來看，這個名字是很形象的。

推廣：從特殊到一般

直線還是曲線？（一般定義式）

這一段沒有什么思維含量，所以直接給過程。

設拋物線\(y=ax^2+bx+c(a\neq 0)\)上有三點\(A(x_1, ax_1^2+bx_1+c), B(x_2, ax_2^2+bx_2+c), C(x_3, ax_3^2+bx_3+c)\)，且\(x_1<x_2<x_3\)。

考慮法\(2\)，證明\(k_{AB}\neq k_{BC}\)。

\[k_{AB}=\frac {(ax_2^2+bx_2+c)-(ax_1^2+bx_1+c)} {x_2-x_1} \]

\[=\frac {a(x_2+x_1)(x_2-x_1)+b(x_2-x_1)} {x_2-x_1} \]

\[\because x_2>x_1\Rightarrow x_2-x_1>0 \]

\[\therefore k_{AB}=a(x_2+x_1)+b \]

\[k_{BC}=\frac {(ax_3^2+bx_3+c)-(ax_2^2+bx_2+c)} {x_3-x_2} \]

\[=\frac {a(x_3+x_2)(x_3-x_2)+b(x_3-x_2)} {x_3-x_2} \]

\[同理，k_{BC}=a(x_3+x_2)+b \]

\[x_1<x_3\Rightarrow x_1+x_2<x_3+x_2 \]

\[\Rightarrow x_1+x_2\neq x_3+x_2 \]

\[\because a\neq 0 \]

\[\therefore a(x_2+x_1)+b\neq a(x_3+x_2)+b \]

\[k_{AB}\neq k_{BC} \]

\[\text {Q.E.D.} \]

接下來讓我們換個順序，先把最值研究掉。

最值（一般定義式）

當時說后面要考的東西，你還記得嗎？

利用平方的非負性，可以快速求出最大值或最小值。

我們先舉個特例，\(y=2x^2+4x-4\)，它有平方嗎？
類似的話你可能在哪里看過。沒錯，就是這里。

配方法：耶！我的用武之地！

\[y=2x^2+4x-4 \]

\[=2(x^2+2x-2) \]

\[=2(x^2+2x+1-3) \]

\[=2(x+1)^2-6 \]

容易看出，當\(x=-1\)時，\(y_{min}=-6\)。

這種是簡單的配方，全程不出現分數的那種。如果出現分數，這種過程很明顯會耗時間（因為常數項先并進括號再乘出去，運算了兩次）。因此，遵循大道至簡的原則，我們把單純的配方法壓成兩步：

幾個問題明確一下。

• 內心\(\text {OS}\)步驟描述：

思考	寫到的步驟
把\(2\)提取出來	\(=2(x^2+2x\)
配完全平方式（一次項一半平方）	\(=2(x^2+2x+1^2)\)
常數項照抄	\(=2(x^2+2x+1^2)-4\)
后面減掉多配的常數項，分配律乘出來	\(=2(x^2+2x+1^2)-4-2\times 1\)
整理，一步得結果	\(=2(x+1)^2-6\)

• 注意！括號內\(1^2\)是為了后面變成平方時方便。如果我們配出的常數項是\((\frac {25} {16})^2=\frac {625}{256}\)，再把\(\frac {625}{256}\)填進括號，第二步又要開方，非常麻煩。
• 括號外\(1\)是為了后面計算方便。事先在配完全平方式時就把常數項算好，整理時就可以直接乘，減少出錯的可能性。
• 腦子必須跟上你的手。相信你親手做一題就明白了。

練習：配方法求函數\(y=x^2-3x+4\)的最值。

參考答案：\(\textcolor{grey}{當x=\frac 3 2時，y_{min}=\frac 7 4。}\)

頂點和頂點式

在上面的特例中，顯然該拋物線的頂點就是\((\frac 3 2, \frac 7 4)\)。現在，讓我們從特殊到一般，探究一下\(y=ax^2+bx+c(a\neq 0)\)的頂點坐標和最值。

很簡單，就是把配方的過程換成純字母嘛。照樣兩步！

拋物線\(y=ax^2+bx+c(a\neq 0)\)的頂點坐標為\((-\frac b {2a}, \frac {4ac-b^2} {4a})\)。

再討論一下最值。為什么用“討論”，應該是很清楚的。

\(①a>0\)：當\(x=-\frac b {2a}\)時，\(y_{min}=\frac {4ac-b^2} {4a}\)；

\(②a<0\)：當\(x=-\frac b {2a}\)時，\(y_{max}=\frac {4ac-b^2} {4a}\)。

最后，隆重介紹一下，我們剛剛化出來的形式

就是蘇科版課本第二種，也是最后一種承認的二次函數形式：

頂點式（\(\text {vertex form}\)）。

由于某些原因（做題你就明白了），它在實際運用中一般寫成

增減性（一般定義式）

根據假設，拋物線頂點左側（即\(x<-\frac b {2a}\)時），\(y\)隨\(x\)的增大而減小；右側（即\(x\ge -\frac b {2a}\)時）相反。

設拋物線\(y=ax^2+bx+c(a\neq 0)\)上有兩點\(A(m, am^2+bm+c), B(n, an^2+bn+c)\)，且\(m<n\)。

\[(am^2+bm+c)-(an^2+bn+c) \]

\[=a(m^2-n^2)+b(m-n) \]

\[=a(m+n)(m-n)+b(m-n) \]

\[=(m-n)[a(m+n)+b] \]

\(①m<n<-\frac b {2a}\)：

\[\because m<-\frac b {2a}, n<-\frac b {2a}\Rightarrow m+n<-\frac b a; \]

\[\Rightarrow a(m+n)+b\dots \]

等等！\(a\)的正負決定了這個多項式的正負！還要討論。

\(1\degree a>0\)：

\[\Rightarrow a(m+n)+b<a\cdot (-\frac b a)+b=0 \]

\[m<n\Rightarrow m-n<0; \]

\[\therefore (m-n)[a(m+n)+b]>0 \]

\[\therefore am^2+bm+c>an^2+bn+c \]

\[y隨x的增大而減小 \]

\(2\degree a<0\)：

\[\Rightarrow a(m+n)+b>a\cdot (-\frac b a)+b=0 \]

\[m<n\Rightarrow m-n<0; \]

\[\therefore (m-n)[a(m+n)+b]<0 \]

\[\therefore am^2+bm+c<an^2+bn+c \]

\[y隨x的增大而增大 \]

\(②-\frac b {2a}\leq m<n\)：

\[\because m\ge -\frac b {2a}, n>-\frac b {2a}\Rightarrow m+n>-\frac b a; \]

\(1\degree a>0\)：

\[\Rightarrow a(m+n)+b>a\cdot (-\frac b a)+b=0 \]

\[m<n\Rightarrow m-n<0; \]

\[\therefore (m-n)[a(m+n)+b]<0 \]

\[\therefore am^2+bm+c<an^2+bn+c \]

\[y隨x的增大而增大 \]

\(2\degree a<0\)：

\[\Rightarrow a(m+n)+b<a\cdot (-\frac b a)+b=0 \]

\[m<n\Rightarrow m-n<0; \]

\[\therefore (m-n)[a(m+n)+b]>0 \]

\[\therefore am^2+bm+c>an^2+bn+c \]

\[y隨x的增大而減小 \]

是的，證明過程就是巨長無比。

結論：對于拋物線\(y=ax^2+bx+c(a\neq 0)\)：

• 當\(a>0\)時：
  • 當\(x<-\frac b {2a}\)時，\(y\)隨\(x\)增大而減小；
  • 當\(x\ge -\frac b {2a}\)時，\(y\)隨\(x\)增大而增大；
• 當\(a>0\)時：
  • 當\(x<-\frac b {2a}\)時，\(y\)隨\(x\)增大而增大；
  • 當\(x\ge -\frac b {2a}\)時，\(y\)隨\(x\)增大而減小；

看來有的時候，我們的假設也會出現錯誤，這是不可避免的。驗證或推翻假設的方法除了證明，還有畫圖。通過圖像我們可以直觀看出函數\(y=-2x^2+3x+4\)的增減性與我們最初的猜想不符。

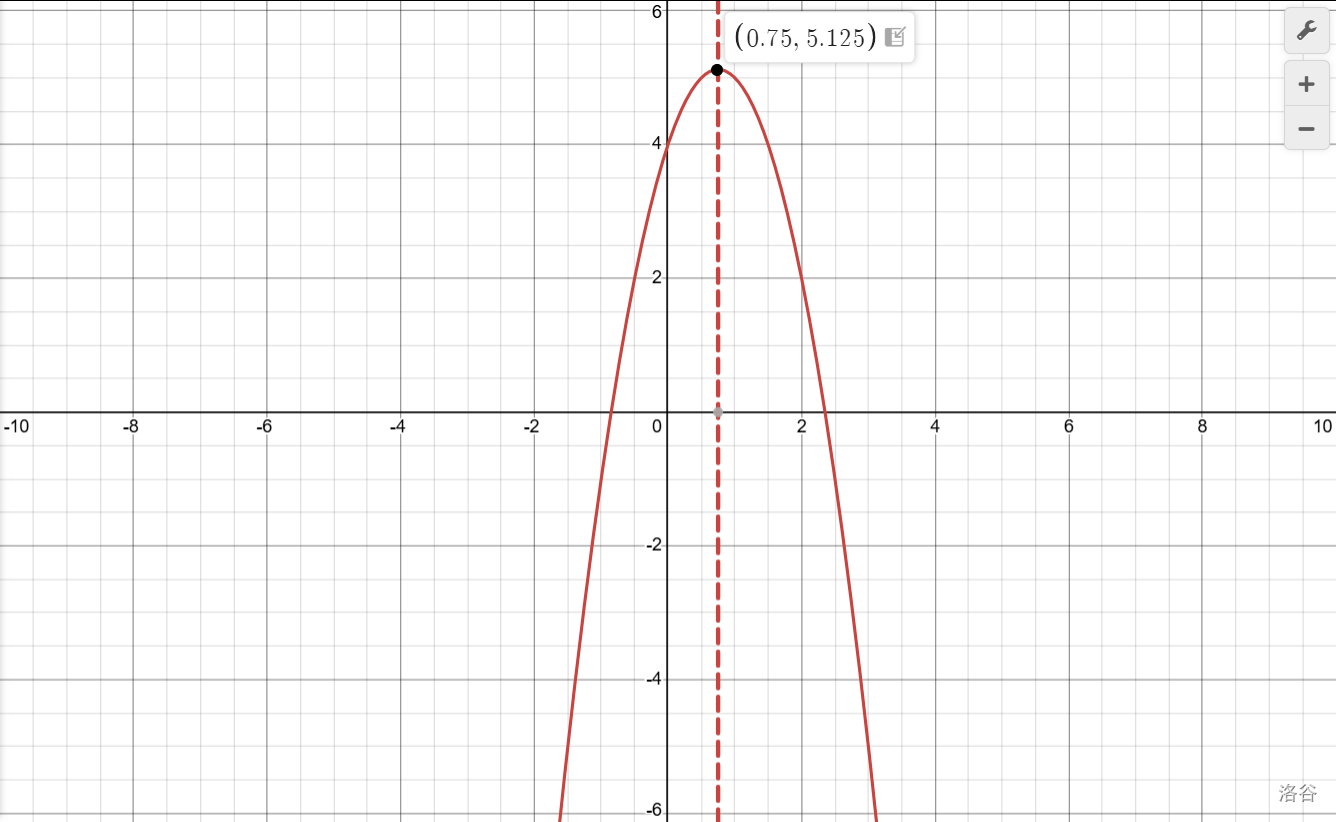
對稱性（一般定義式）

根據假設，我們認為拋物線的對稱軸為通過其頂點的垂直于\(x\)軸的直線，即直線\(x=-\frac b {2a}\)。

設拋物線\(y=ax^2+bx+c(a\ne 0)\)上有一點\(A(m, am^2+bm+c)\)。

點\(A\)關于直線\(x=-\frac b {2a}\)的對稱點是……

算了，如果你沒學過口訣（中間兩倍減頭）的話，那還是老老實實設成\(A'(x, am^2+bm+c)\)。根據中點公式，有：

\[\frac {m+x} 2=-\frac b {2a} \]

\[x=-\frac b a-m=-\frac {am+b} a \]

\[\therefore A'(-\frac {am+b} a, am^2+bm+c) \]

\[\because a(-\frac {am+b} a)^2+b(-\frac {am+b} a)+c \]

\[=\frac {(am+b)^2} a-\frac {b(am+b)} a+c \]

\[=\frac {a^2m^2+2abm+b^2-abm-b^2} a+c \]

\[=\frac {a(am^2+bm)} a+c \]

\[a\neq 0\Rightarrow 原式=am^2+bm+c \]

\[\therefore 點A'在直線x=-\frac b {2a}上 \]

\[\text {Q.E.D.} \]

開口大小和方向

拿書上的探究舉例子吧，我們研究\(y=ax^2(a\ne 0)\)的圖像隨\(a\)取值變化的變化情況。

準備好我們的實驗器材方格紙，打好坐標系。

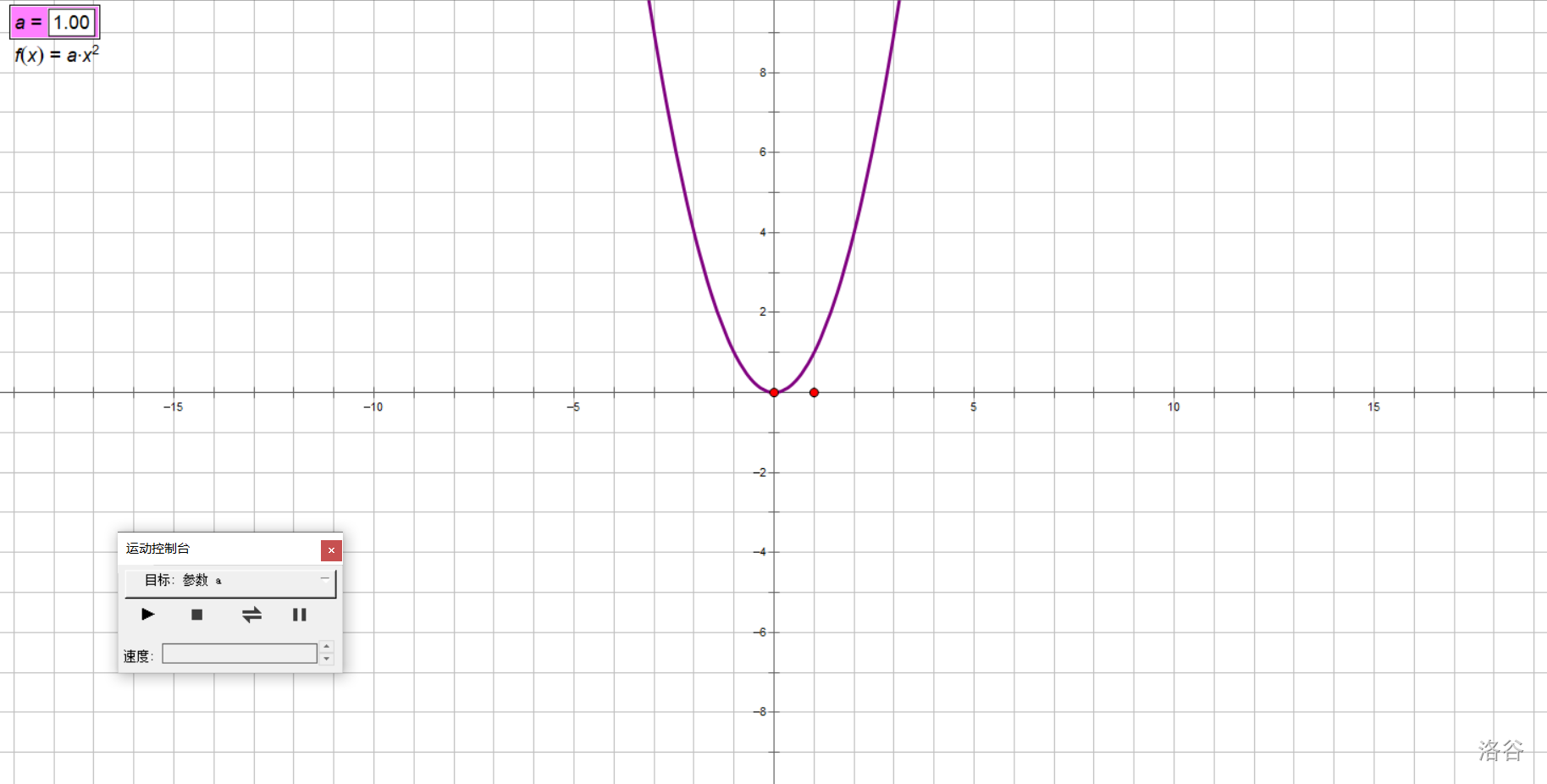
讓\(a\)動起來！

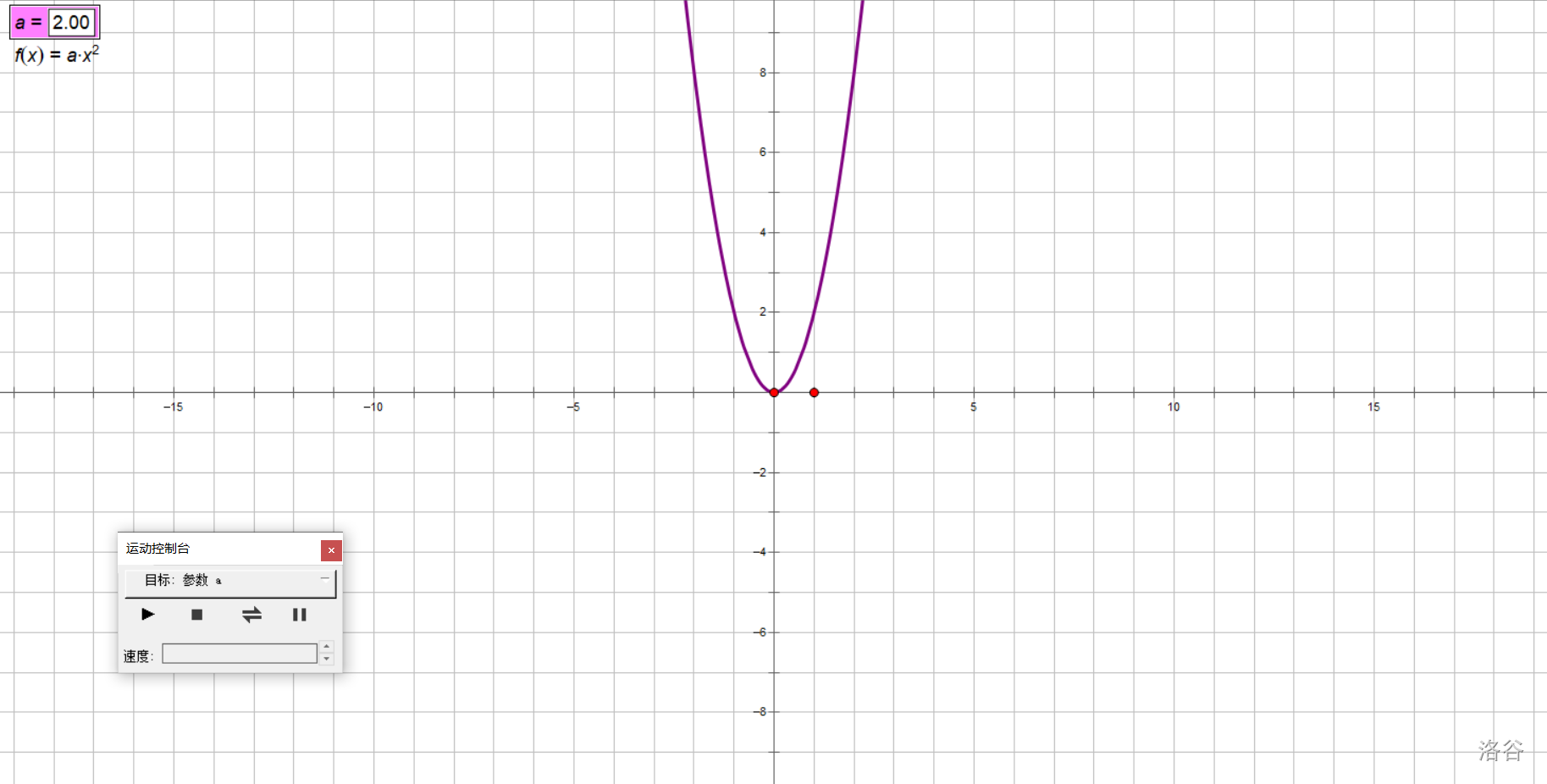
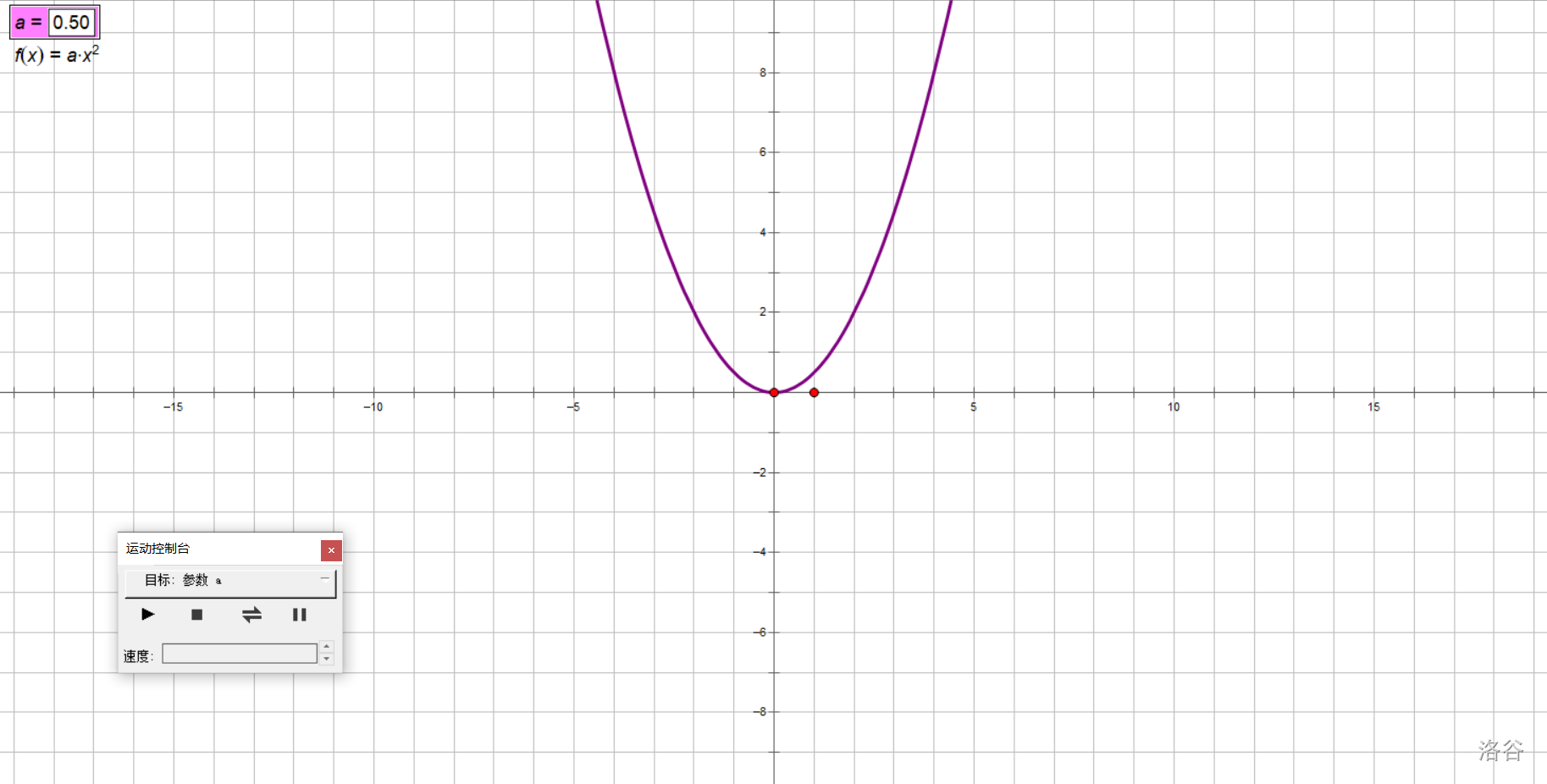
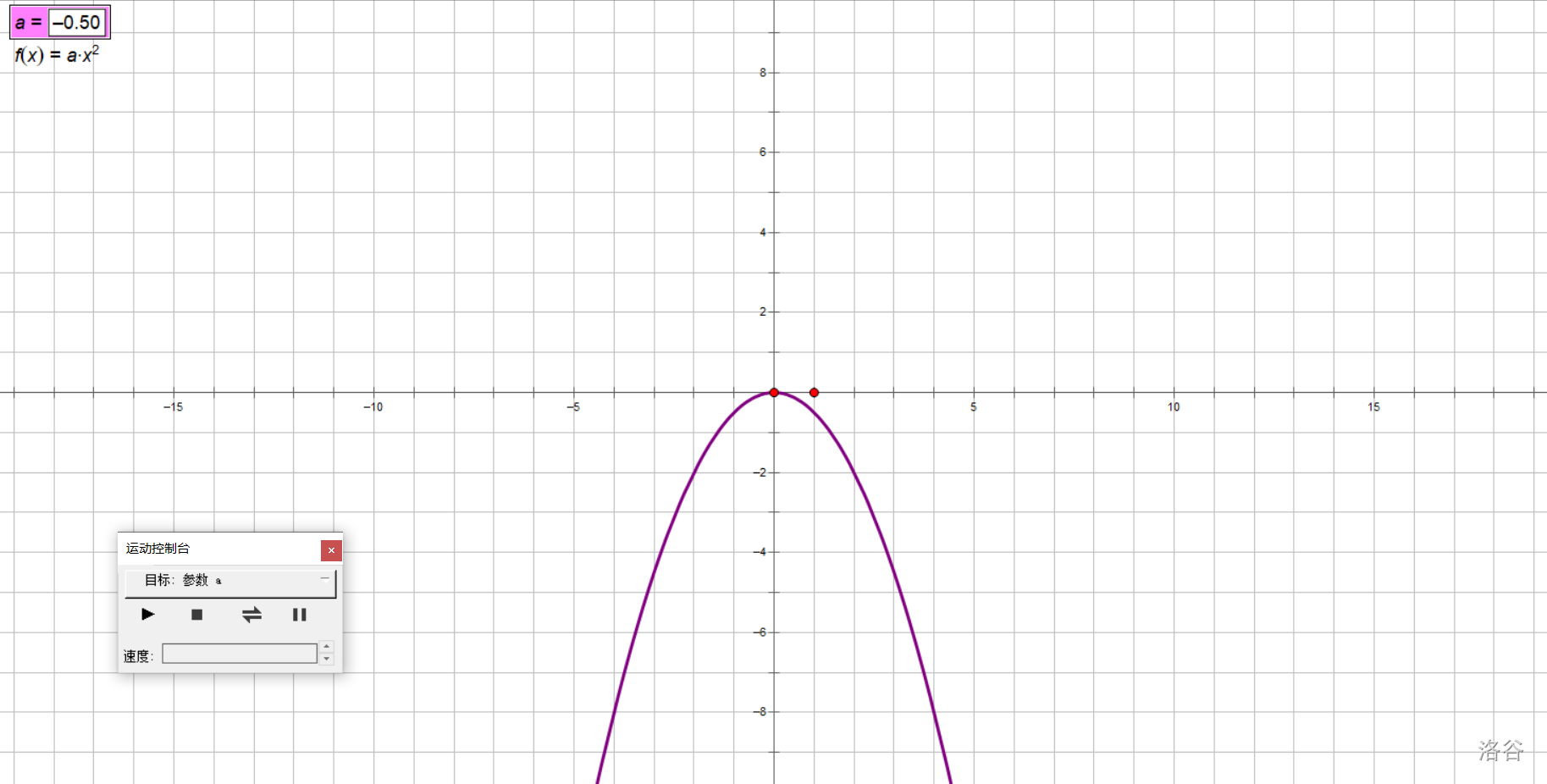
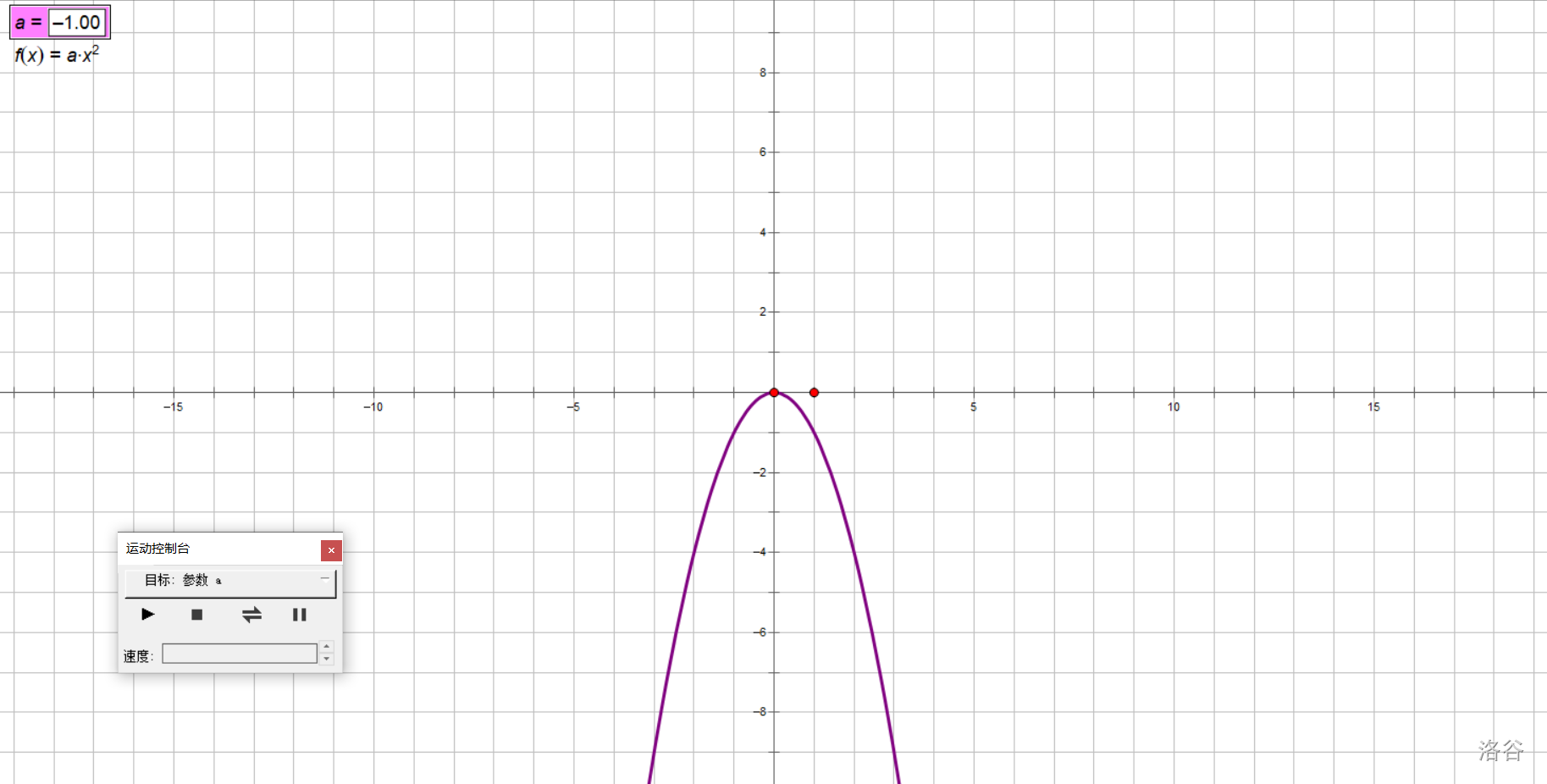
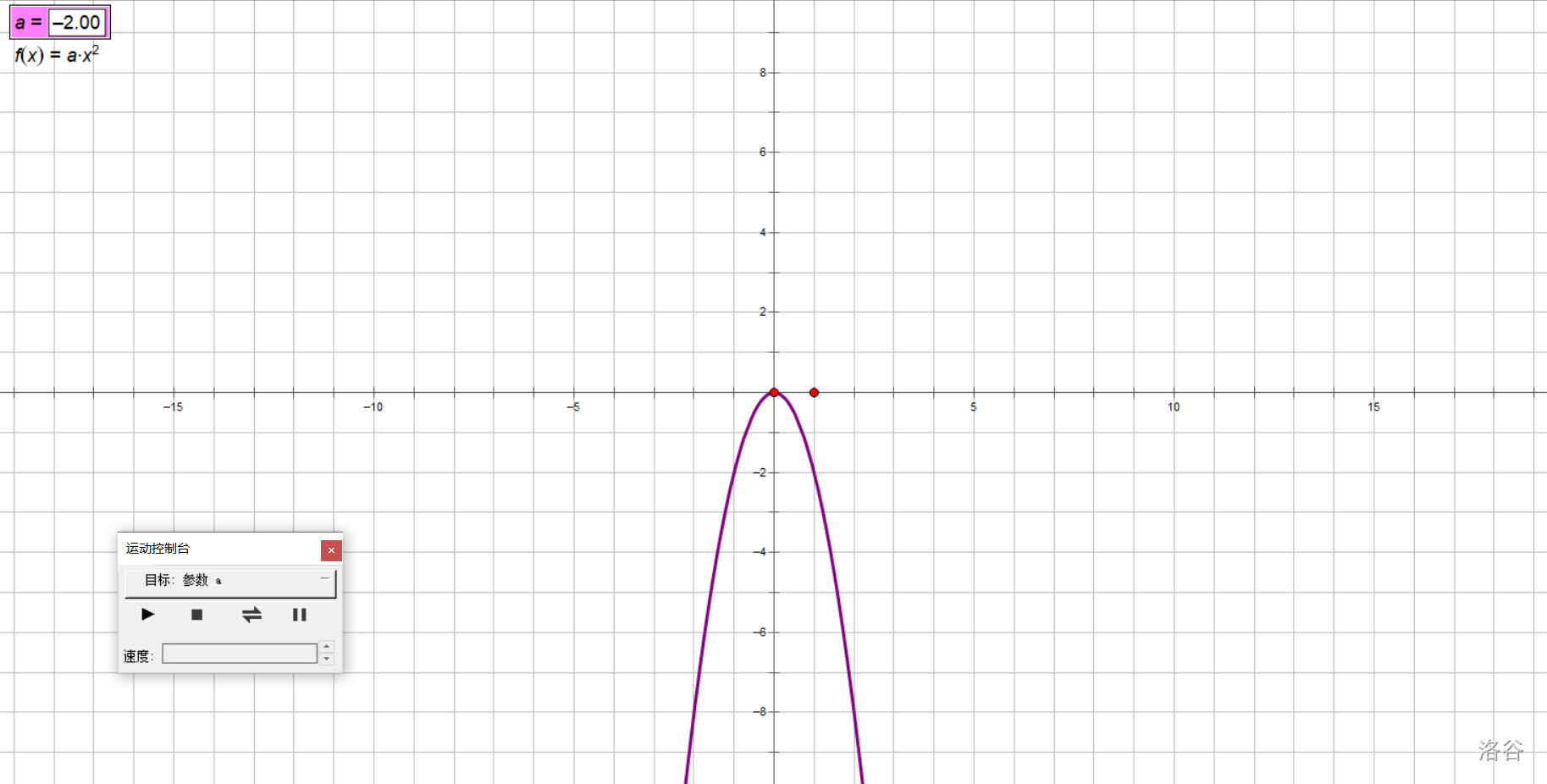
在實驗中，我們讓\(a\)從大到小，從正到負變化，得出以下結論：

對于拋物線\(y=ax^2(a\neq 0)\)：

• 當\(a>0\)時，開口朝上，\(a\)越小，開口越大；
• 當\(a<0\)時，開口朝下，\(a\)越大，開口越大。

兩句話的后半部分可以合并為：

• （無論\(a\)正負）\(|a|\)越小，開口越大；\(|a|\)越大，開口越小。

至于這個結論能否應用于所有的拋物線中，請聽下回分解。

變換：“移一移”

左加右減，上加下減，大道也。

函數\(y=(x+3)^2\)的圖像和函數\(y=x^2\)的圖像有什么關系？
聰明的你一定能想到，向左平移了\(3\)格。

那函數\(y=2(x+3)^2\)的圖像和\(y=2x^2\)的有什么關系？
那當然還是向左平移了\(3\)格。

上難度！函數\(y=2(x+3)^2+114514\)和\(y=2x^2\)呢？
根據“大道”，顯然是向左平移\(3\)格，向上平移\(114514\)格。

最后一問！函數\(y=a(x+h)^2+k\)和\(y=ax^2\)呢……

哦！原來頂點式的本質就是平移！原來的\(y=ax^2\)頂點是\((0,0)\)，向左平移\(h\)格，向上平移\(k\)格就是頂點式！而且，由于頂點也按照這種方式平移，因而我們很快得出，其頂點為\((-h, k)\)。

再由于頂點式都可以被化為定義式：

\[y=a(x+h)^2+k=ax^2+2ahx+k \]

\[(a'=a, b'=2ah, c'=k) \]

因此得到一個驚人結論：

任意拋物線\(y=ax^2+bx+c(a\ne 0)\)，都可以由\(y=ax^2\)平移而來。平移方法我就不贅述了，先化成頂點式即可。

這也解答了上面的疑問，關于開口大小和開口方向的結論適用于任意拋物線。