吳恩達深度學習課程一:神經(jīng)網(wǎng)絡和深度學習 第四周:深層神經(jīng)網(wǎng)絡的關(guān)鍵概念 課后作業(yè)和代碼實踐
此分類用于記錄吳恩達深度學習課程的學習筆記。
課程相關(guān)信息鏈接如下:
- 原課程視頻鏈接:[雙語字幕]吳恩達深度學習deeplearning.ai
- github課程資料,含課件與筆記:吳恩達深度學習教學資料
- 課程配套練習(中英)與答案:吳恩達深度學習課后習題與答案
本篇為第一課第四周的課程練習部分的講解。
1.理論習題
【中英】【吳恩達課后測驗】Course 1 - 神經(jīng)網(wǎng)絡和深度學習 - 第四周測驗
同樣,這是本周理論部分的習題和相應解析,博主已經(jīng)做好了翻譯和解析工作。
這里單獨選出一道題如下:
向量化允許您在L層神經(jīng)網(wǎng)絡中計算前向傳播,而不需要在層(l = 1,2,…,L)上顯式的使用for-loop(或任何其他顯式迭代循環(huán)),正確嗎?
答案:錯誤
通過這道題,我們來總結(jié)一下:
向量化后的神經(jīng)網(wǎng)絡,到底省去了哪些部分的顯式循環(huán)?又有哪些循環(huán)始終不能省去?
1.1 非向量化的神經(jīng)網(wǎng)絡需要定義哪些循環(huán)?
在沒有向量化之前,前向傳播過程通常包含以下顯式循環(huán):
| 循環(huán)類型 | 作用對象 | 描述 |
|---|---|---|
| 輪次循環(huán)(Epoch) | 整個訓練集反復訓練的次數(shù) | 為了不斷優(yōu)化參數(shù),必須多次重復訓練整個訓練集,每一輪稱為一個 Epoch。 |
| 批次循環(huán)(Batch) | 每一個批次 | 若使用小批次梯度下降,則每輪訓練需要對所有批次依次執(zhí)行前向和反向傳播。(一批次訓練所有樣本則不需此行) |
| 樣本循環(huán) | 每個樣本 | 對訓練集中的每個樣本單獨計算前向傳播和損失(在未向量化時存在)。 |
| 層循環(huán) | 每一層 | 逐層計算:當前層的輸出依賴上一層輸出,因此必須按順序執(zhí)行,無法并行消除。 |
| 層內(nèi)神經(jīng)元循環(huán) | 當前層的每個神經(jīng)元 | 計算當前層每個神經(jīng)元的加權(quán)和與激活(可被矩陣運算替代)。 |
| 特征循環(huán) | 某個神經(jīng)元內(nèi)部所有輸入特征 | 對輸入特征逐一乘權(quán)重再求和,即實現(xiàn)一次點乘(可向量化消除)。 |
1.2 向量化的神經(jīng)網(wǎng)絡省去了哪些循環(huán)?
向量化后,再次總結(jié)如下:
| 循環(huán)類型 | 是否被消除 | 原因說明 |
|---|---|---|
| 輪次循環(huán)(Epoch) | 無法消除 | 每一輪訓練都需更新參數(shù),是梯度下降優(yōu)化的外層結(jié)構(gòu),與是否向量化無關(guān)。 |
| 批次循環(huán)(Batch) | 無法消除 | Mini-batch 是訓練策略的一部分,用于節(jié)省顯存與穩(wěn)定梯度,無法用矩陣運算替代。(一批次訓練所有樣本則不需此行) |
| 樣本循環(huán) | 被消除 | 向量化使得矩陣 ( \(X=[x^{(1)}, x^{(2)}, ...]\) ) 可以一次性處理所有樣本,無需逐個 for。 |
| 層循環(huán) | 無法消除 | 每層的輸出依賴上一層結(jié)果,必須逐層計算,屬于模型結(jié)構(gòu)依賴,無法并行消除,只是代碼中可不寫顯式 for。 |
| 層內(nèi)神經(jīng)元循環(huán) | 被消除 | 矩陣乘法 ( \(Z = W A + b\) ) 可一次計算整層所有神經(jīng)元的輸出,無需逐神經(jīng)元循環(huán)。 |
| 特征循環(huán) | 被消除 | 神經(jīng)元加權(quán)求和(點乘)由底層線性代數(shù)庫以矩陣計算形式完成,無需手工遍歷每個特征。 |
這里要單獨說明一下層循環(huán),層循環(huán)不同于輪次和批次,他不會直接使用顯示的 for 語法。
層循環(huán)的本質(zhì)是輸入樣本的處理順序,我們只有在前一層得到結(jié)果后才可以進行下一層的計算,這樣嚴密的串行結(jié)構(gòu)無法并行消除。
因此,我們才說習題里的說法是錯誤的。
1.3表格總結(jié)
| 循環(huán)類型 | 是否可向量化消除 |
|---|---|
| 輪次循環(huán) | 不可消除 |
| 批次循環(huán) | 不可消除 |
| 層循環(huán) | 不可消除 |
| 樣本循環(huán) | 可消除 |
| 層內(nèi)神經(jīng)元循環(huán) | 可消除 |
| 特征循環(huán) | 可消除 |
2.代碼實踐:多層神經(jīng)網(wǎng)絡
吳恩達神經(jīng)網(wǎng)絡實戰(zhàn)第四周同樣先粘貼整理課程習題的博主答案,博主依舊在不借助很多現(xiàn)在流行框架的情況下手動構(gòu)建模型的各個部分,并手動實現(xiàn)傳播,計算過程。
如果希望更扎實地了解原理,更推薦跟隨這位博主的內(nèi)容一步步手動構(gòu)建模型,這樣對之后框架的使用也會更得心應手。
這次實操不同于之前直接使用框架構(gòu)建,我們在本周的理論部分里了解了正向傳播和反向傳播的模塊化,再回看一下定義:
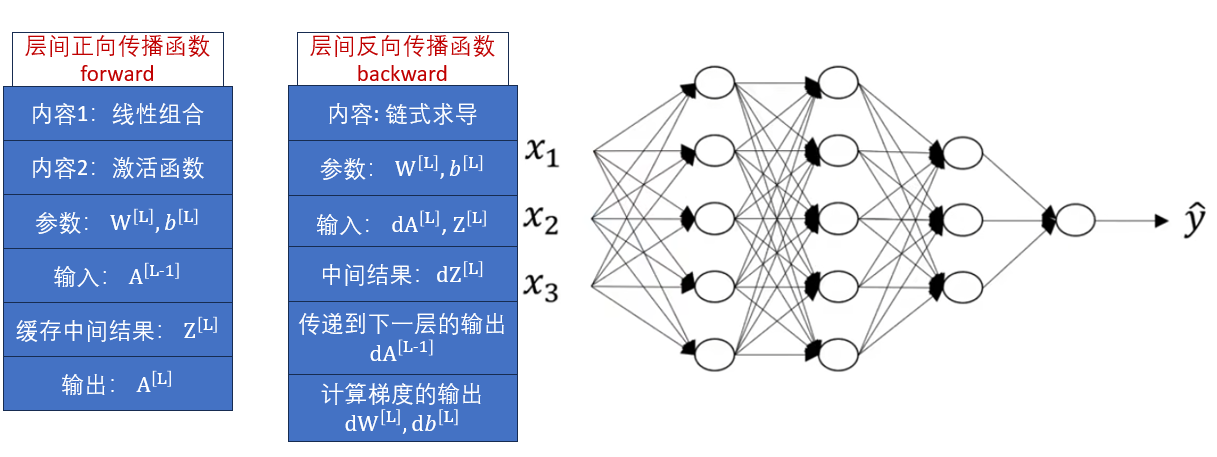
這次,我們按照理論梳理的內(nèi)容,看看如何實現(xiàn)這兩個函數(shù)。
之后,再使用框架來看看多層神經(jīng)網(wǎng)絡對損失,對最終準確率的影響。
2.1 手工實現(xiàn)傳播
1.正向傳播
import numpy as np
# 1.定義ReLU激活函數(shù)用于隱藏層
def ReLU(Z):
return np.maximum(0, Z),Z # 返回格式:(層輸出,加權(quán)和)
# 2.定義Sigmoid 激活函數(shù)用于輸出層
def sigmoid(Z):
return 1/(1+np.exp(-Z)),Z # 返回格式:(層輸出,加權(quán)和)
# 3.向前傳播函數(shù),實現(xiàn)線性組合+激活函數(shù)
def forward(A_prev, W, b, activation):
"""
參數(shù)介紹:
A_prev : 上一層輸出 A^[L-1]
W : 當前層權(quán)重 W^[L]
b : 當前層偏置 b^[L]
activation : 本層使用的激活函數(shù)
"""
# 3.1 線性組合 Z = W*A_prev + b
Z = np.dot(W, A_prev) + b
# 3.2 激活函數(shù)
if activation == "sigmoid":
A, Z_cache = sigmoid(Z)
elif activation == "ReLU":
A, Z_cache = ReLU(Z)
else:
raise ValueError("未定義該激活函數(shù)")
# 3.3 保存中間值供 backward 使用
cache = (A_prev, W, b, Z_cache)
return A, cache
"""
返回:
A : 當前層輸出 A^[L]
cache : 緩存中間結(jié)果 (A_prev, W, b, Z),用于反向傳播
"""
2.反向傳播
import numpy as np
# 1. 激活函數(shù)的導數(shù)實現(xiàn)
def dReLU(dA, Z):
"""
ReLU 導數(shù):
f(Z) = max(0, Z)
f'(Z) = 1, 若 Z > 0
0, 若 Z <= 0
"""
# dZ = dA*f'(Z)
dZ = np.array(dA, copy=True) # **確保修改dZ時不會影響到原始的dA
dZ[Z <= 0] = 0 # 只有 Z>0 時梯度能傳遞
return dZ
def dSigmoid(dA, Z):
"""
Sigmoid 導數(shù):
A = σ(Z) = 1/(1 + e^-Z)
f'(Z) = A * (1 - A)
"""
A = 1 / (1 + np.exp(-Z))
# dZ = dA*f'(Z)
dZ = dA * A * (1 - A)
return dZ
# 2. 反向傳播函數(shù)(鏈式求導得到參數(shù)梯度)
def backward(dA, cache, activation):
"""
參數(shù):
dA : 當前層損失對激活輸出 A^[L] 的梯度
cache : 前向傳播保存的中間結(jié)果 (A_prev, W, b, Z)
activation : 本層使用的激活函數(shù)
"""
# 2.1取出前向傳播緩存
A_prev, W, b, Z = cache
m = A_prev.shape[1] # 樣本數(shù)量 m
# 2.2 根據(jù)激活函數(shù)計算 dZ
if activation == "ReLU":
dZ = dReLU(dA, Z)
elif activation == "sigmoid":
dZ = dSigmoid(dA, Z)
else:
raise ValueError("未定義的激活函數(shù)")
# 2.3 線性部分梯度(公式對應):
# dW = 1/m * dZ * A_prev^T
# db = 1/m * ∑(dZ)
# dA_prev = W^T * dZ
dW = (1/m) * np.dot(dZ, A_prev.T)
db = (1/m) * np.sum(dZ, axis=1, keepdims=True)
dA_prev = np.dot(W.T, dZ)
return dA_prev, dW, db
"""
返回:
dA_prev : 傳遞給上一層的梯度
dW : 當前層權(quán)重的梯度
db : 當前層偏置的梯度
"""
這樣,我們就實現(xiàn)了多層神經(jīng)網(wǎng)絡層間的正向傳播和反向傳播函數(shù),如有更多興趣可以去最開始推薦的博主的博客內(nèi),看看手工搭建整個神經(jīng)網(wǎng)絡的過程。
2.2 搭建多層神經(jīng)網(wǎng)絡
我們在第三周的代碼實踐中搭建的淺層神經(jīng)網(wǎng)絡的代碼如下:
class ShallowNeuralNetwork(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten() #
# 隱藏層:輸入128*128*3維特征,輸出4個神經(jīng)元
self.hidden = nn.Linear(128 * 128 * 3, 4)
# 隱藏層激活函數(shù):ReLU,作用是加入非線性特征
self.ReLU = nn.ReLU()
# 輸出層:將隱藏層的 4 個輸出映射為 1 個加權(quán)和
self.output = nn.Linear(4, 1)
self.sigmoid = nn.Sigmoid()
# 前向傳播方法
def forward(self, x):
# 輸入 x 的維度為 [32, 3, 128, 128]
x = self.flatten(x)
# 展平后 x 的維度為 [32, 128 * 128 * 3]
x = self.hidden(x)
# 通過隱藏層線性變換后,x 的維度為 [32, 4]
x = self.ReLU(x)
# 經(jīng)過 ReLU 激活后形狀不變,仍為 [32, 4]
x = self.output(x)
# 通過輸出層得到加權(quán)和,形狀變?yōu)?[32, 1]
x = self.sigmoid(x)
# 經(jīng)過 sigmoid 激活后得到 0~1 的概率值,形狀仍為 [32, 1]
return x
現(xiàn)在,我們再按本周理論內(nèi)容里的多層神經(jīng)網(wǎng)絡修改一下,不改變其他部分:
經(jīng)過三次代碼實踐,本周的內(nèi)容里也總結(jié)了層級間維度變化的規(guī)律,想必對這部分的代碼內(nèi)容已經(jīng)很熟悉了。這次就不再添加詳細注釋。
class ShallowNeuralNetwork(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
# 隱藏層
self.hidden1 = nn.Linear(128 * 128 * 3, 5)
self.hidden2 = nn.Linear(5, 5)
self.hidden3 = nn.Linear(5, 3)
self.ReLU = nn.ReLU()
# 輸出層
self.output = nn.Linear(3, 1)
self.sigmoid = nn.Sigmoid()
def forward(self, x):
x = self.flatten(x)
x = self.hidden1(x)
x = self.ReLU(x)
x = self.hidden2(x)
x = self.ReLU(x)
x = self.hidden3(x)
x = self.ReLU(x)
x = self.output(x)
x = self.sigmoid(x)
return x
其構(gòu)建的網(wǎng)絡結(jié)構(gòu)為:

很容易就可以對應出來。
2.3 結(jié)果分析
從淺層神經(jīng)網(wǎng)絡到多層神經(jīng)網(wǎng)絡,網(wǎng)絡的規(guī)模再次擴大,帶來的效果是什么樣的呢?
我們還是先看結(jié)果:
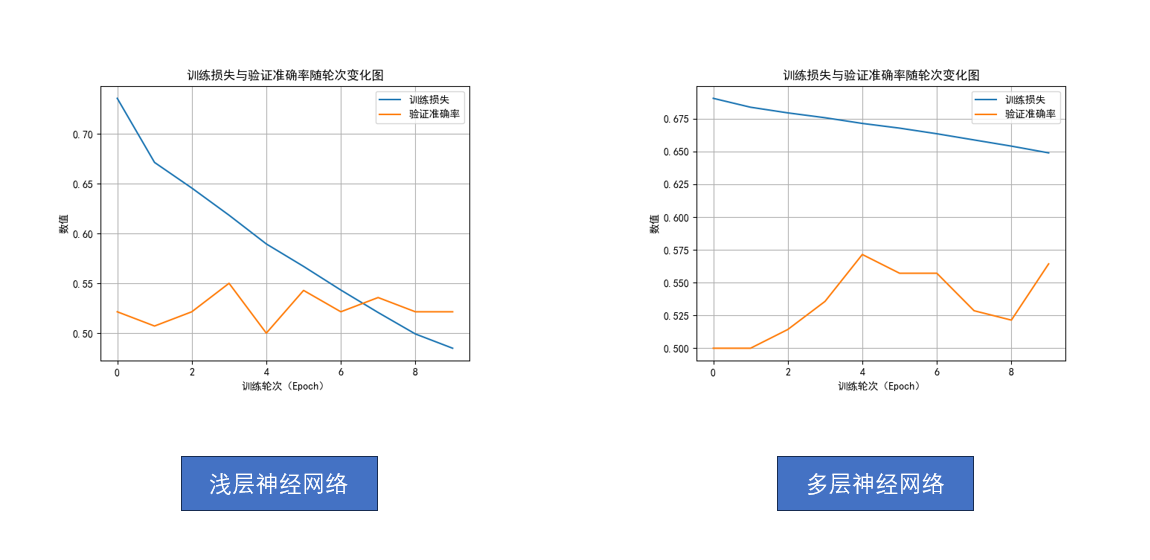
不對。
不是哥們,多了兩層隱藏層,準確率沒怎么升,損失收斂速度還變慢了?
先別急,回憶一下,在第三周,我們對比的是邏輯回歸和淺層神經(jīng)網(wǎng)絡,從結(jié)果上我們得到的是淺層神經(jīng)網(wǎng)絡極大降低了損失。
當時為了控制變量,我們統(tǒng)一設置訓練輪次為10輪。
但有個容易忽略的前提——
當時的網(wǎng)絡結(jié)構(gòu)比較簡單,10輪訓練足夠讓它收斂。
而現(xiàn)在我們提升到了多層神經(jīng)網(wǎng)絡,模型容量更大、表達的函數(shù)更復雜,再加上學習率設置得不高,僅僅訓練10輪,根本不足以發(fā)揮出它的潛力。
我們可以把它想象成:一場賽跑,淺層網(wǎng)絡和多層網(wǎng)絡都跑10圈,淺層網(wǎng)絡更快,但它已經(jīng)精疲力竭了,而后者剛剛結(jié)束熱身。
為了讓復雜的網(wǎng)絡得到更充分的訓練,現(xiàn)在我們把訓練輪次增加到100輪。
再次分別運行兩個網(wǎng)絡模型,來對比一下:
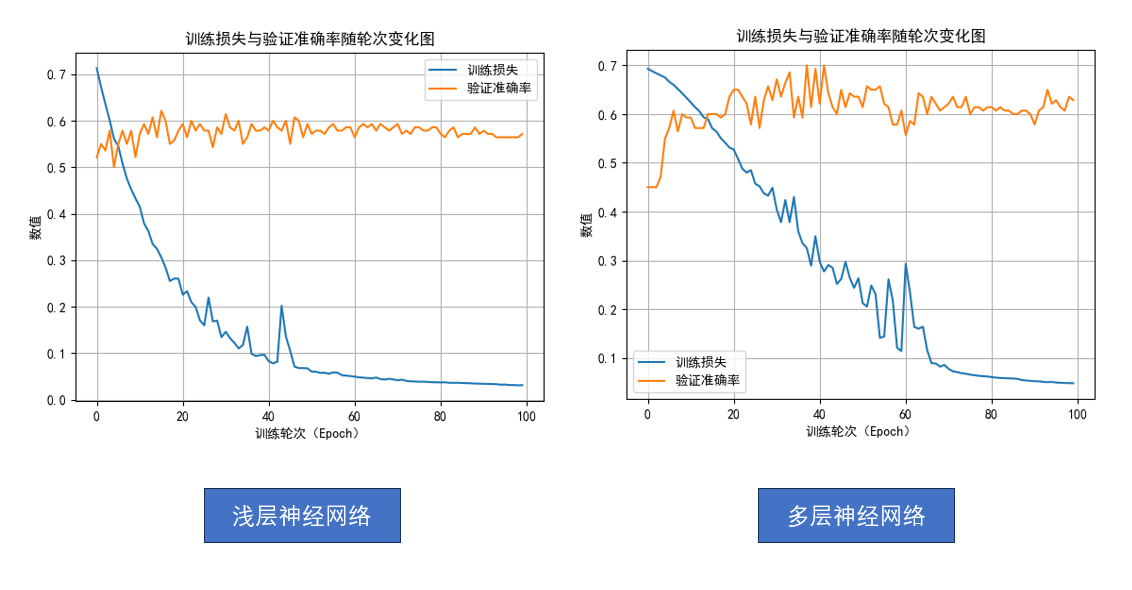
現(xiàn)在,是不是就能發(fā)現(xiàn)差別了?
- 淺層神經(jīng)網(wǎng)絡:即使訓練到100輪,準確率依舊徘徊在 60% 左右,最高也難突破。
- 多層神經(jīng)網(wǎng)絡:在大約第30輪后準確率迅速提升,最高甚至接近 70%,之后也很少跌回 60% 以下。
這就是我們之前提到的模型的“想象力”。
網(wǎng)絡越深、參數(shù)越多,它越有能力去刻畫復雜的函數(shù)關(guān)系,但反過來,它也需要更多時間和數(shù)據(jù)去學習,否則就像一位天賦很高但沒受過訓練的選手,潛力被埋沒了。
這就是多層神經(jīng)網(wǎng)絡的效果。
3.總結(jié)
自此,吳恩達老師的深度學習第一課的筆記內(nèi)容就結(jié)束了。
最后簡單總結(jié)一下:
第一周,神經(jīng)網(wǎng)絡簡介,從概念上簡單介紹了神經(jīng)網(wǎng)絡。
第二周,用邏輯回歸這個單神經(jīng)元網(wǎng)絡講解最簡單的神經(jīng)網(wǎng)絡的傳播過程。
第三周,從邏輯回歸網(wǎng)絡擴展到淺層神經(jīng)網(wǎng)絡,講解隱藏層的作用和傳播過程。
第四周,從淺層神經(jīng)網(wǎng)絡擴展到多層神經(jīng)網(wǎng)絡,補充更多細節(jié)和直觀效果。
總的來說,第一課還是比較基礎(chǔ)的內(nèi)容。
之后的第二課開始就會以神經(jīng)網(wǎng)絡為基礎(chǔ),以實際網(wǎng)絡運行為引,介紹其中的各種問題和解決方案,技術(shù),會更加偏實踐一些,也會更有“訓練AI”的感覺。
最后附一下這次的多層神經(jīng)網(wǎng)絡完整代碼:
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms
from torch.utils.data import DataLoader, random_split
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score
transform = transforms.Compose([
transforms.Resize((128, 128)),
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))
])
dataset = datasets.ImageFolder(root='./cat_dog', transform=transform)
train_size = int(0.8 * len(dataset))
val_size = int(0.1 * len(dataset))
test_size = len(dataset) - train_size - val_size
train_dataset, val_dataset, test_dataset = random_split(dataset, [train_size, val_size, test_size])
train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True)
val_loader = DataLoader(val_dataset, batch_size=32, shuffle=False)
test_loader = DataLoader(test_dataset, batch_size=32, shuffle=False)
class ShallowNeuralNetwork(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
# 隱藏層
self.hidden1 = nn.Linear(128 * 128 * 3, 5)
self.hidden2 = nn.Linear(5, 5)
self.hidden3 = nn.Linear(5, 3)
self.ReLU = nn.ReLU()
# 輸出層
self.output = nn.Linear(3, 1)
self.sigmoid = nn.Sigmoid()
def forward(self, x):
x = self.flatten(x)
x = self.hidden1(x)
x = self.ReLU(x)
x = self.hidden2(x)
x = self.ReLU(x)
x = self.hidden3(x)
x = self.ReLU(x)
x = self.output(x)
x = self.sigmoid(x)
return x
model = ShallowNeuralNetwork()
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model.to(device)
criterion = nn.BCELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)
epochs =10
train_losses = []
val_accuracies = []
for epoch in range(epochs):
model.train()
epoch_train_loss = 0
for images, labels in train_loader:
images, labels = images.to(device), labels.to(device).float().unsqueeze(1)
outputs = model(images)
loss = criterion(outputs, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
epoch_train_loss += loss.item()
avg_train_loss = epoch_train_loss / len(train_loader)
train_losses.append(avg_train_loss)
model.eval()
val_true, val_pred = [], []
with torch.no_grad():
for images, labels in val_loader:
images = images.to(device)
outputs = model(images)
preds = (outputs.cpu().numpy() > 0.5).astype(int).flatten()
val_pred.extend(preds)
val_true.extend(labels.numpy())
val_acc = accuracy_score(val_true, val_pred)
val_accuracies.append(val_acc)
print(f"輪次: [{epoch + 1}/{epochs}], 訓練損失: {avg_train_loss:.4f}, 驗證準確率: {val_acc:.4f}")
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.plot(train_losses, label='訓練損失')
plt.plot(val_accuracies, label='驗證準確率')
plt.title("訓練損失與驗證準確率隨輪次變化圖")
plt.xlabel("訓練輪次(Epoch)")
plt.ylabel("數(shù)值")
plt.legend()
plt.grid(True)
plt.show()
model.eval()
y_true, y_pred = [], []
with torch.no_grad():
for images, labels in test_loader:
images = images.to(device)
outputs = model(images)
preds = (outputs.cpu().numpy() > 0.5).astype(int).flatten()
y_pred.extend(preds)
y_true.extend(labels.numpy())
acc = accuracy_score(y_true, y_pred)
print(f"測試準確率: {acc:.4f}")



 浙公網(wǎng)安備 33010602011771號
浙公網(wǎng)安備 33010602011771號