吳恩達(dá)深度學(xué)習(xí)課程一:神經(jīng)網(wǎng)絡(luò)和深度學(xué)習(xí) 第三周:淺層神經(jīng)網(wǎng)絡(luò)(一)正向傳播
此分類用于記錄吳恩達(dá)深度學(xué)習(xí)課程的學(xué)習(xí)筆記。
課程相關(guān)信息鏈接如下:
- 原課程視頻鏈接:[雙語字幕]吳恩達(dá)深度學(xué)習(xí)deeplearning.ai
- github課程資料,含課件與筆記:吳恩達(dá)深度學(xué)習(xí)教學(xué)資料
- 課程配套練習(xí)(中英)與答案:吳恩達(dá)深度學(xué)習(xí)課后習(xí)題與答案
本篇為第一課第三周,3.1到3.5部分的筆記內(nèi)容。
經(jīng)過第二周的基礎(chǔ)補(bǔ)充,本周內(nèi)容的理解難度可以說有了很大的降低,主要是從邏輯回歸擴(kuò)展到淺層神經(jīng)網(wǎng)絡(luò),講解相關(guān)內(nèi)容,我們按部就班梳理課程內(nèi)容即可,當(dāng)然,依舊會盡可能地創(chuàng)造一個較為絲滑的理解過程。
1.神經(jīng)網(wǎng)絡(luò)
1.1 邏輯回歸的網(wǎng)絡(luò)結(jié)構(gòu)
在第二周我們已經(jīng)知道,邏輯回歸是通過一次線性組合和sigmoid激活函數(shù)來進(jìn)行二分類的算法,現(xiàn)在,我們用神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)來描述一下邏輯回歸,如下圖所示:
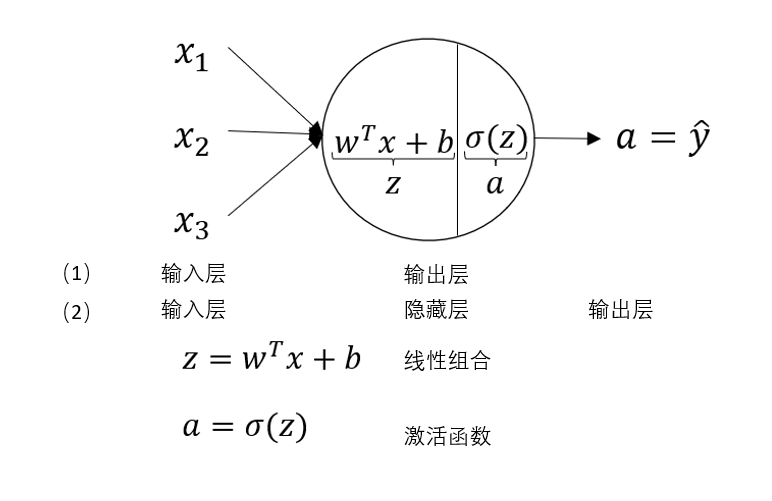
對于輸入層,隱藏層,輸出層,我們在第一周的內(nèi)容里就已經(jīng)進(jìn)行過相關(guān)介紹。
為什么在這里寫了兩種層級劃分形式呢?
我們回到之前總結(jié)的內(nèi)容:邏輯回歸 =線性組合+sigmoid
一般來說,對于二分類問題,我們會在輸出層設(shè)置 sigmoid 激活函數(shù),來對隱藏層的輸出再進(jìn)行最終的組合和映射。
但邏輯回歸的結(jié)構(gòu)過于簡單,它的內(nèi)容只有一次線性組合和sigmoid,而這二者在一個神經(jīng)元里即可完成設(shè)置。
因此,我們可以把邏輯回歸的網(wǎng)絡(luò)看作沒有隱藏層,又或者輸出層不做任何處理。
這些都是結(jié)構(gòu)上的劃分,我們明白意思,知道算法的內(nèi)容即可。
最后總結(jié)一下邏輯回歸,可以說,邏輯回歸的核心還是對數(shù)據(jù)進(jìn)行線性擬合,只是其經(jīng)過sigmoid輸出的是概率而非直接的數(shù)值。
在上周的代碼實踐部分中,我們也能發(fā)現(xiàn),邏輯回歸展現(xiàn)出的性能略顯不足。
我們通過邏輯回歸了解了一個最簡單的神經(jīng)網(wǎng)絡(luò)的運行過程,而現(xiàn)在就需要更進(jìn)一步了。
1.2 一個淺層神經(jīng)網(wǎng)絡(luò)的網(wǎng)絡(luò)結(jié)構(gòu)
來看這樣一個稍復(fù)雜點的神經(jīng)網(wǎng)絡(luò):
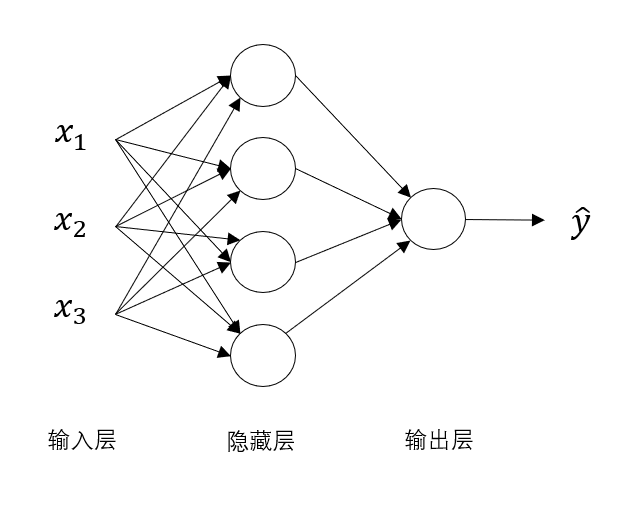
很明顯,隱藏層神經(jīng)元從一個變成了四個,每一個神經(jīng)元的結(jié)構(gòu)都和剛剛包含線性組合和激活函數(shù)的神經(jīng)元一樣。
一直以來,我們都有這樣的認(rèn)知:更復(fù)雜的神經(jīng)網(wǎng)絡(luò)能擬合更復(fù)雜的數(shù)據(jù),得到更好的模型。
而現(xiàn)在,面對這個比邏輯回歸復(fù)雜了一些的淺層神經(jīng)網(wǎng)絡(luò),它又是如何做到更好的擬合效果呢?
我們用淺層神經(jīng)網(wǎng)絡(luò)再來一次傳播。
2.淺層神經(jīng)網(wǎng)絡(luò)的正向傳播
在之前的向量化學(xué)習(xí)內(nèi)容中,我們知道了邏輯回歸,即只有一個隱藏神經(jīng)元的神經(jīng)網(wǎng)絡(luò)的正向傳播過程,而現(xiàn)在我們來看一下淺層神經(jīng)網(wǎng)絡(luò)的正向傳播。
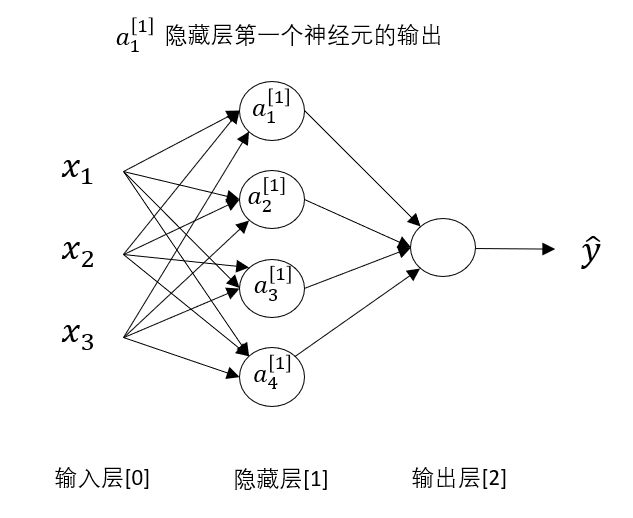
先引入一些新的符號。
在之前的內(nèi)容里,我們知道:
- \(x^{(i)}\) 中的 \(i\) 代表第 \(i\) 個樣本
- \(x_i\) 中的 \(i\) 代表某個樣本的第 \(i\) 個變量
現(xiàn)在,我們對神經(jīng)網(wǎng)絡(luò)的層級進(jìn)行劃分,規(guī)定:\(x^{[i]}\) 中的 \(i\) 代表這個量來自第 \(i\) 層。
我們按照課程內(nèi)容對各層劃分,規(guī)定輸入層為第0層,此后依次增加。
要說明的是并非隱藏層就是第1層,輸出就是第2層,只是這個淺層神經(jīng)網(wǎng)絡(luò)中只有一層隱藏層,所以輸出是第2層。
因此,如圖所示: \(a^{[1]}_1\) 就代表第一層第一個神經(jīng)元的輸出。
現(xiàn)在,我們系統(tǒng)地梳理一遍淺層神經(jīng)網(wǎng)絡(luò)的向量化正向傳播過程:
2.1 輸入特征
沒有變化:
- 對于單個樣本:
- 對于一個批次,\(m\) 個樣本:
2.2 隱藏層的參數(shù)設(shè)置
這里我們按上面的網(wǎng)絡(luò)結(jié)構(gòu)定為4個隱藏神經(jīng)元:
- 對于單個神經(jīng)元,其權(quán)重向量為:
- 現(xiàn)在,我們把4個神經(jīng)元的權(quán)重向量組合在一起得到隱藏層權(quán)重矩陣\(W^{[1]}\),其中每一行 \(\mathbf{w^{[1]}_i}\)
是連接輸入層到第 \(i\) 個隱藏神經(jīng)元的權(quán)重向量。
- 同理,我們得到偏置矩陣:
要說明的是,我們已經(jīng)知道了廣播機(jī)制,所以現(xiàn)在\(\mathbf{b^{[1]}}\)中的每個量都是標(biāo)量,在進(jìn)行加權(quán)和運算時會自動向右復(fù)制為 \(m\) 列來配合運算,不直接定義為一個標(biāo)量是因為每個神經(jīng)元的偏置不同。
2.3 隱藏層的線性加權(quán)和
最終,我們向量化的線性組合公式如下:
我們展開來看一下\(\mathbf{Z^{[1]}}\) 的具體內(nèi)容:
再細(xì)化一下:
這樣,我們就得到了一批次樣本在分別在四個隱藏神經(jīng)元上線性組合得到的加權(quán)和。
2.4 隱藏層的激活函數(shù)
每個隱藏神經(jīng)元的輸出為:
其中 \(g(x)\) 是激活函數(shù)(例如 ReLU、tanh、sigmoid)。
到這里,我們就得到了隱藏層的輸出,同時,這也是輸出層的輸入。
2.5 輸出層的參數(shù)設(shè)置
輸出層只有一個神經(jīng)元,用來生成最終的預(yù)測值。
我們先再看一眼輸入\(\mathbf{A^{[1]}}\) ,他代表的是一批次樣本在分別在四個隱藏神經(jīng)元上的輸出,其中每一個元素就代表一個樣本經(jīng)過一個隱藏層神經(jīng)元的輸出。
再說到行列:
\(\mathbf{A^{[1]}}\) 的一行代表所有樣本在一個隱藏神經(jīng)元上的輸出,一列代表一個樣本在所有隱藏神經(jīng)元上的輸出。
按計算的位置來說,在這里一個樣本在每個隱藏神經(jīng)元上的輸出和之前的每個樣本的輸入特征相同
我們再次進(jìn)行線性組合,依然要以樣本為單位。
- 權(quán)重向量如下,再次強(qiáng)調(diào)區(qū)分: 隱藏層存在多個神經(jīng)元,所以 \(\mathbf{W^{[1]}}\)里的每個元素是向量,而輸出層只有一個神經(jīng)元,所以 \(\mathbf{W^{[2]}}\)里的每個元素是標(biāo)量。
- 偏置矩陣如下,其列數(shù)和該層神經(jīng)元數(shù)量相同。
2.6 輸出層的線性組合和激活
公式如下:
如果說 \(\mathbf{A^{[1]}}\) 的每個元素代表了一個樣本在經(jīng)過各個輸入特征加權(quán)后的中間表達(dá)結(jié)果,那么 \(\mathbf{A^{[2]}}\) 的每個元素便進(jìn)一步綜合了該樣本在所有隱藏神經(jīng)元上的響應(yīng),得到該樣本在輸出層的最終預(yù)測值。
從這句話,或許便可以從邏輯上來幫助理解更復(fù)雜的網(wǎng)絡(luò)能得到更好的擬合效果的原因。
2.7 總結(jié)
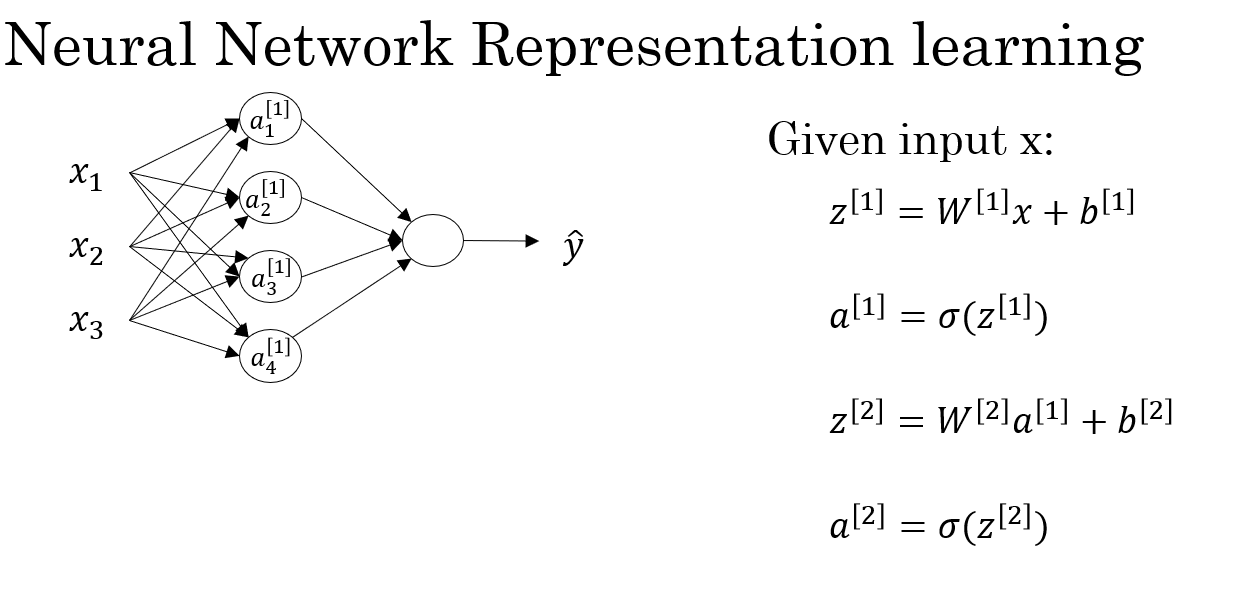
這便是課程中給出的總結(jié)部分,一次正向傳播實際上便是四個公式的運算,我們也總結(jié)一下本次過程中各種量的變化如下:
| 層級 | 符號 | 含義 | 維度 |
|---|---|---|---|
| 輸入層 | ?? | 所有輸入樣本 | (n × m) |
| 隱藏層權(quán)重 | \(W^{[1]}\) | 輸入→隱藏層連接 | (4 × n) |
| 隱藏層偏置 | \(b^{[1]}\) | 每個神經(jīng)元偏置 | (4 × 1) |
| 隱藏層線性輸出 | \(Z^{[1]}\) | 加權(quán)和 | (4 × m) |
| 隱藏層激活 | \(A^{[1]}\) | 非線性輸出 | (4 × m) |
| 輸出層權(quán)重 | \(W^{[2]}\) | 隱藏層→輸出層連接 | (1 × 4) |
| 輸出層偏置 | \(b^{[2]}\) | 輸出層偏置 | (1 × 1) |
| 輸出層線性輸出 | \(Z^{[2]}\) | 加權(quán)和 | (1 × m) |
| 最終輸出 | \(A^{[2]}\) | 模型預(yù)測 | (1 × m) |
下一篇會再展開一下激活函數(shù)來敘述復(fù)雜網(wǎng)絡(luò)提高擬合能力的原因,并梳理淺層神經(jīng)網(wǎng)絡(luò)如何應(yīng)用梯度下降,即反向傳播的過程。



 浙公網(wǎng)安備 33010602011771號
浙公網(wǎng)安備 33010602011771號