??奇異值分解是一個有著很明顯的物理意義的一種方法,它可以將一個比較復(fù)雜的矩陣用更小更簡單的幾個子矩陣的相乘來表示,這些小矩陣描述的是矩陣的重要的特性。就像是描述一個人一樣,給別人描述說這個人長得濃眉大眼,方臉,絡(luò)腮胡,而且?guī)€黑框的眼鏡,這樣寥寥的幾個特征,就讓別人腦海里面就有一個較為清楚的認(rèn)識,實際上,人臉上的特征是有著無數(shù)種的,之所以能這么描述,是因為人天生就有著非常好的抽取重要特征的能力,讓機(jī)器學(xué)會抽取重要的特征,SVD是一個重要的方法。
??所以SVD不僅是一個數(shù)學(xué)問題,在工程應(yīng)用方面很多地方都有其身影,如PCA,推薦系統(tǒng)、任意矩陣的滿秩分解。
??博主整理這篇博客就是為后面深度神經(jīng)網(wǎng)絡(luò)的模型壓縮做準(zhǔn)備。
參考論文:A Singularly Valuable Decomposition The SVD of a Matrix
1、特征值
如果說一個向量v是方陣A的特征向量,將一定可以表示成下面的形式:
??????????
這時候λ被稱為特征向量v對應(yīng)的特征值,一個矩陣的一組特征向量是一組正交向量。特征值分解是將一個矩陣分解成以下形式:
??????????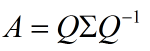
??其中Q是這個矩陣A的特征向量組成的矩陣,Σ是一個對角陣,每個對角線上的元素就是一個特征值。和矩陣相乘其實就是一次線性變換。如一下兩個例子:
??????????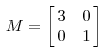
其對應(yīng)的線形變換是一下形式:
??????????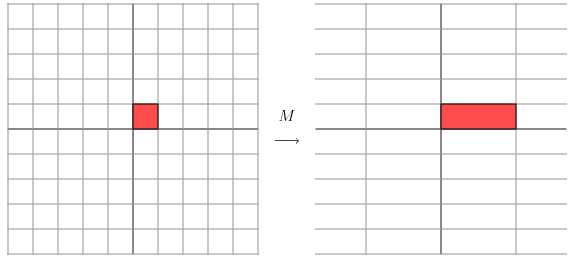
我們可以根據(jù)數(shù)學(xué)的計算看到更加直觀的結(jié)果:
??????????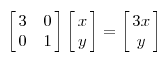
注意兩點:
1、對角陣對角線上的特征值的絕對值大于1時,特征值越大拉伸的幅度越大,特征值絕對值小于1,特征值越小壓縮的幅度越大;
2、這只是矩陣為對角陣的情況下,拉伸和收縮都是沿著坐標(biāo)軸(也就是特征向量)的方向,而對于非對稱的非對角陣,會有非坐標(biāo)軸方向的拉伸和收縮
??我們想要描述好一個變換,那我們就描述好這個變換主要的變化方向就好了,而對角陣Σ里面的特征值是由大到小排列的,特征值對應(yīng)的特征向量就是描述矩陣的變化方向。
??當(dāng)矩陣是高緯度的時候,矩陣就是高緯度空間下的線形變換,通過特征值分解得到的前N個向量就是矩陣最主要的N個變化的方向。利用這N個方向的變化來近似這個矩陣。也就是:提取這個矩陣最重要的一部分特征。(而特征值分解的局限就是變換的矩陣必須為方陣)
2、正交矩陣
??正交矩陣是在歐幾里得空間里的叫法,在酉空間里叫酉矩陣,一個正交矩陣對應(yīng)的變換叫正交變換,這個變換的特點是不改變向量的尺寸和向量間的夾角。下圖是一個直觀的認(rèn)識: 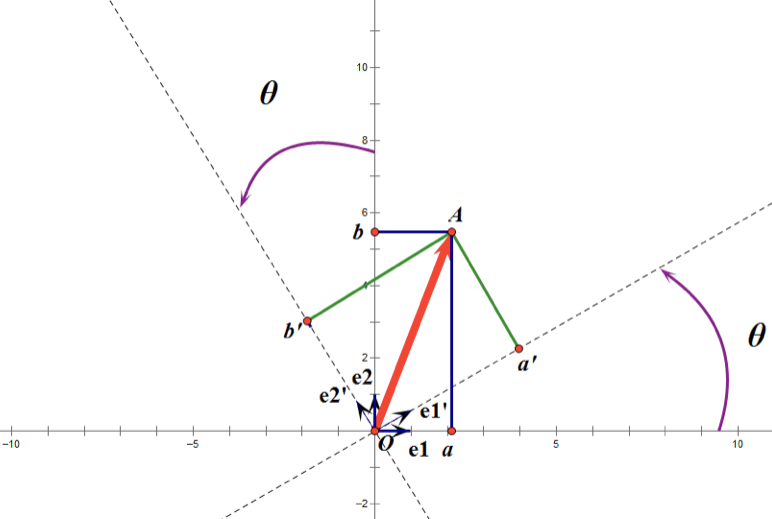
??假設(shè)二維空間中的向量OA,它在標(biāo)準(zhǔn)坐標(biāo)系(也就是e1和e2表示的坐標(biāo)系)中的表示為(a,b)’(‘表示轉(zhuǎn)置);現(xiàn)在用另一組坐標(biāo)e1’、e2’表示為(a’,b’)’;那么存在矩陣U使得(a’,b’)’=U(a,b)’,而矩陣U就是正交矩陣。
??通過上圖可知,正交變換只是將變換向量用另一組正交基來表示,在這個過程中并沒有罪向量作拉伸,也不改變向量的空間位置,對兩個向量同時做正交變換,變換的前后兩個向量的夾角顯然也不會改變。上圖是一個旋轉(zhuǎn)的正交變換,可以把e1’、e2’坐標(biāo)系看做是e1、e2坐標(biāo)系經(jīng)過旋轉(zhuǎn)某個θ角度得到,具體的旋轉(zhuǎn)規(guī)則如下:
????????????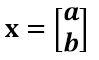
????????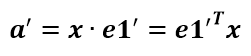
????????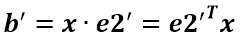
a’和b’實際上是x在e1’和e2’軸上投影的大小,所以直接做內(nèi)積可得:
????????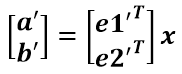
從圖中可以看到:
????????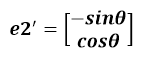
所以:
????????
??正交矩陣U的行(列)之間都是單位正交向量,它對向量做旋轉(zhuǎn)變換。這里解釋一下:旋轉(zhuǎn)是相對的,就那上面的圖來說,我們可以說向量的空間位置沒有變,標(biāo)準(zhǔn)參考系向左旋轉(zhuǎn)了θ角度,而如果我選擇了e1’、e2’作為新的標(biāo)準(zhǔn)坐標(biāo)系,那么在新坐標(biāo)系中OA(原標(biāo)準(zhǔn)坐標(biāo)系的表示)就變成了OA’,這樣看來就好像坐標(biāo)系不動,把OA往順時針方向旋轉(zhuǎn)了θ角度,這個操作實現(xiàn)起來很簡單:將變換后的向量坐標(biāo)仍然表示在當(dāng)前坐標(biāo)系中。
??正交變換的另一個方面是反射變換,也即e1’的方向與圖中方向相反。
??總結(jié):正交矩陣的行(列)向量都是兩兩正交的單位向量,正交矩陣對應(yīng)的變換為正交變換,它有兩種表現(xiàn):旋轉(zhuǎn)和反射。正交矩陣將標(biāo)準(zhǔn)正交基映射為標(biāo)準(zhǔn)正交基(即圖中從e1、e2到e1’、e2’)。
3、特征值的分解 - EVD
??在討論SVD之前,先了解矩陣的特征值分解(EVD),這里選擇特殊的矩陣——對角陣,對稱矩陣又一個性質(zhì)就是總能相似對角化,對稱矩陣不同特征值對應(yīng)的特征向量兩兩正交。一個矩陣能能相似對角化即說明其特征子空間即為其列空間,若不能對角化則其特征子空間為列空間的子空間。現(xiàn)在假設(shè)存在m * m的滿秩對稱矩陣A,它有m個不同的特征值,設(shè)特征值為:
??????????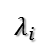
對應(yīng)的單位特征向量:
??????????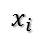
則有:
????????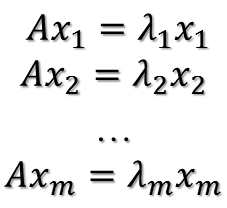
進(jìn)而:
????????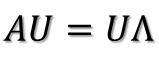
????????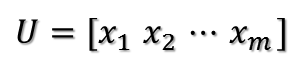
????????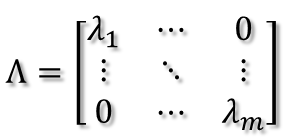
所以可得到A的特征值分解(由于對稱陣特征向量兩兩正交,所以U為正交陣,正交陣的逆矩陣等于其轉(zhuǎn)置):
????????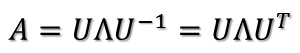
這里假設(shè)A有m個不同的特征值,實際上,只要A是對稱陣其均有如上分解。
矩陣A分解了,相應(yīng)的,其對應(yīng)的映射也分解為三個映射。現(xiàn)在假設(shè)有x向量,用A將其變換到A的列空間中,那么首先由UT先對x做變換:
????????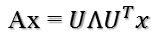
U是正交陣UT也是正交陣,所以UT對x的變換是正交變換,它將x用新的坐標(biāo)系來表示,這個坐標(biāo)系就是A的所有正交的特征向量構(gòu)成的坐標(biāo)系。比如將x用A的所有特征向量表示為:
????????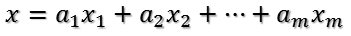
則通過第一個變換就可以把x表示為[a1 a2 … am]T: 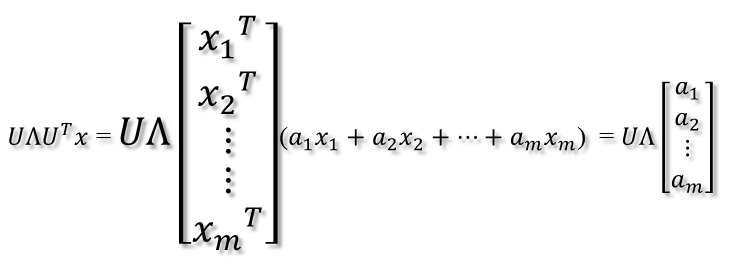
緊接著,在新的坐標(biāo)系表示下,由中間那個對角矩陣對新的向量坐標(biāo)換,其結(jié)果就是將向量往各個軸方向拉伸或壓縮: 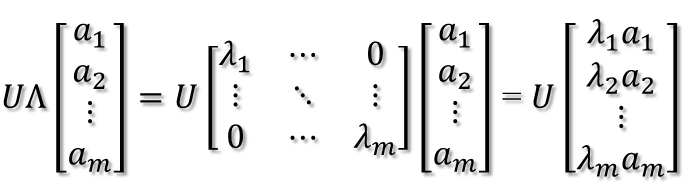
從上圖可以看到,如果A不是滿秩的話,那么就是說對角陣的對角線上元素存在0,這時候就會導(dǎo)致維度退化,這樣就會使映射后的向量落入m維空間的子空間中。
最后一個變換就是U對拉伸或壓縮后的向量做變換,由于U和UT是互為逆矩陣,所以U變換是UT變換的逆變換。
因此,從對稱陣的分解對應(yīng)的映射分解來分析一個矩陣的變換特點是非常直觀的。假設(shè)對稱陣特征值全為1那么顯然它就是單位陣,如果對稱陣的特征值有個別是0其他全是1,那么它就是一個正交投影矩陣,它將m維向量投影到它的列空間中。
根據(jù)對稱陣A的特征向量,如果A是2 * 2的,那么就可以在二維平面中找到這樣一個矩形,是的這個矩形經(jīng)過A變換后還是矩形: 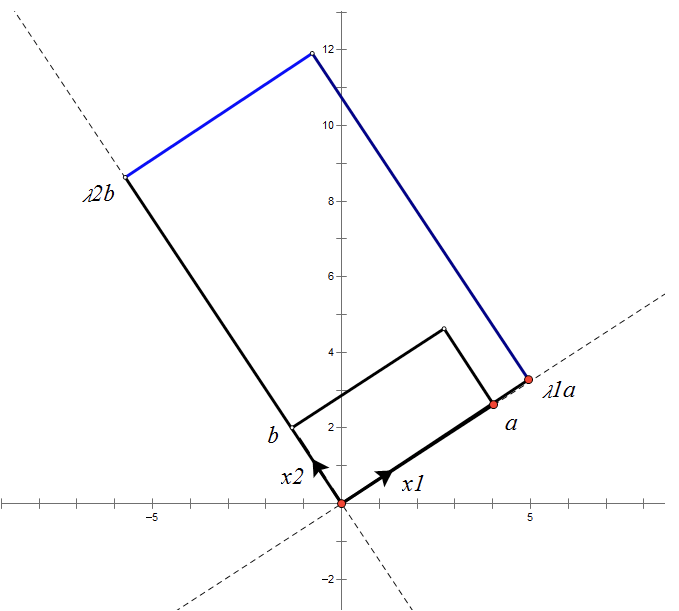
這個矩形的選擇就是讓其邊都落在A的特征向量方向上,如果選擇其他矩形的話變換后的圖形就不是矩形了!
4、奇異值
??上面說過了特征值分解是提取矩陣特征很不錯的方法,但這只是針對方陣而言的,在現(xiàn)實世界中大部分的矩陣并不是方針,這時描述這些普通矩陣的重要特征就會用到:奇異值分解。他是可以適應(yīng)任意矩陣分解的方法:
??????????????
??假設(shè)A是一個M * N的矩陣,那么得到的U是一個M * M的方陣(里面的向量是正交的,U里面的向量稱為左奇異向量),Σ是一個M * N的矩陣(除了對角線的元素都是0,對角線上的元素稱為奇異值),V’(V的轉(zhuǎn)置)是一個N * N的矩陣,里面的向量也是正交的,V里面的向量稱為右奇異向量),從圖片來反映幾個相乘的矩陣的大小可得下面的圖片: 
那么矩陣A的奇異值和方陣的特征值是如何對應(yīng)的?
我們將一個矩陣AT * A,將會得到一個方陣,我們用這個方陣求特征值可以得到:
??????????
這里得到的Vi就是上面的右奇異向量,此外,我們可以得到:
??????????
這里的σi就是上面說的奇異值。ui就是上面的左奇異向量。奇異值σ跟特征值相似,在矩陣Σ中也是按從大到小的方式排列,而且σ的值減小的特別的快,在很多的情況下前10%甚至1%的奇異值之和就占了全部奇異值之和的99%以上。也就是說可以用前r個大的奇異值來近似的描述矩陣,這里定義奇異值的分解:
??????????
r是一個遠(yuǎn)遠(yuǎn)小于m和n的值,矩陣的乘法看起來是這個樣子: 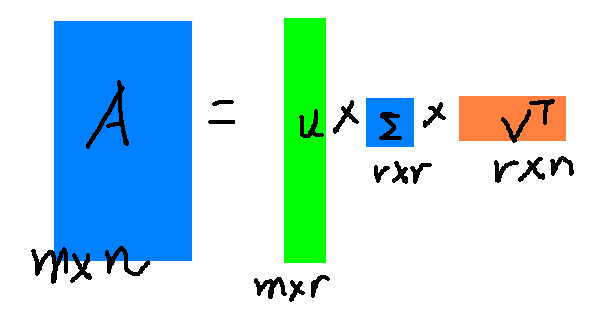
??右邊的三個矩陣相乘的結(jié)果將會是一個接近于A的矩陣,在這兒,r越接近于n,則相乘的結(jié)果越接近于A。而這三個矩陣的面積之和(在存儲觀點來說,矩陣面積越小,存儲量就越小)要遠(yuǎn)遠(yuǎn)小于原始的矩陣A,我們?nèi)绻胍獕嚎s空間來表示原矩陣A,我們存下這里的三個矩陣:U、Σ、V就好了。
5、奇異值分解 - SVD
??上面的特征值分解的A矩陣是對稱陣,根據(jù)EVD可以找到一個(超)矩形使得變換后還是(超)矩形,也即A可以將一組正交基映射到另一組正交基!那么現(xiàn)在來分析:對任意M*N的矩陣,能否找到一組正交基使得經(jīng)過它變換后還是正交基?答案是肯定的,它就是SVD分解的精髓所在。
??現(xiàn)在假設(shè)存在M*N矩陣A,事實上,A矩陣將n維空間中的向量映射到k(k<=m)維空間中,k=Rank(A)。現(xiàn)在的目標(biāo)就是:在n維空間中找一組正交基,使得經(jīng)過A變換后還是正交的。假設(shè)已經(jīng)找到這樣一組正交基:
??????????????{v1,v2,v3,…,vn}
則A矩陣將這組基映射為:
??????????????{Av1,Av2,Av3,…,Avn}
如果要使他們兩兩正交,即:
??????????????Avi · Avj = (Avi)TAvj = viTATAvj = 0
根據(jù)假設(shè),存在:
??????????????viTvj = vivj = 0
所以如果正交基v選擇為ATA的特征向量的話,由于ATA是對稱陣,v之間兩兩正交,那么:
??????????????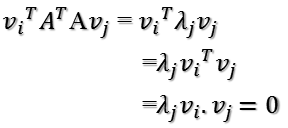
這樣就找到了正交基使其映射后還是正交基了,現(xiàn)在,將映射后的正交基單位化,因為:
??????????????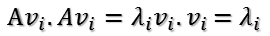
所以有:
??????????????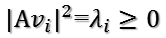
所以取單位向量:
??????????????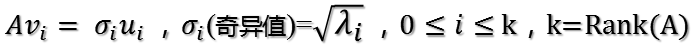
當(dāng)k < i <= m時,對u1,u2,…,uk進(jìn)行擴(kuò)展u(k+1),…,um,使得u1,u2,…,um為m維空間中的一組正交基,即將{u1,u2,…,uk}正交基擴(kuò)展成{u1,u2,…,um}Rm空間的單位正交基,同樣的,對v1,v2,…,vk進(jìn)行擴(kuò)展v(k+1),…,vn(這n-k個向量存在于A的零空間中,即Ax=0的解空間的基),使得v1,v2,…,vn為n維空間中的一組正交基,即:
在A的零空間中選擇{vk+1,vk+2,…,vn}使得AvI = 0,i > k并取σ = 0則可得到:
繼而得到A矩陣的奇異值分解:
??????????????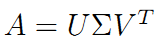
V是n*n的正交矩陣,U是m*m的正交矩陣,Σ是m*n的對角陣
現(xiàn)在可以來對A矩陣的映射過程進(jìn)行分析了:如果在n維空間中找到一個(超)矩形,其邊都落在ATA的特征向量的方向上,那么經(jīng)過A變換后的形狀仍然為(超)矩形!
vi為ATA的特征向量,稱為A的右奇異向量,ui=Avi實際上為AAT的特征向量,稱為A的左奇異向量。下面利用SVD證明文章一開始的滿秩分解:
利用矩陣分塊乘法展開得:
可以看到第二項為0,有: 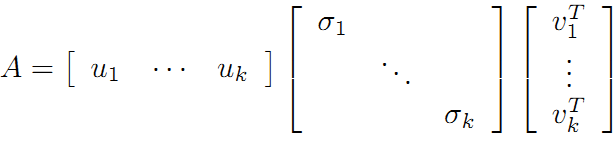
令: 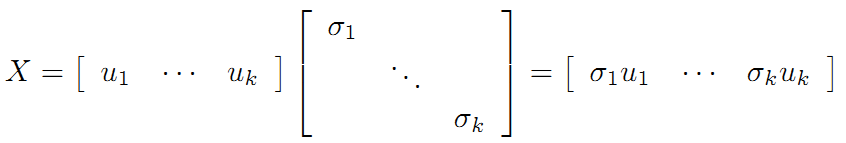
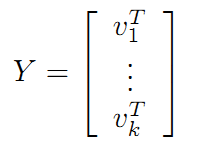
則A=XY即是A的滿秩分解。


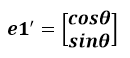
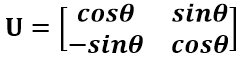
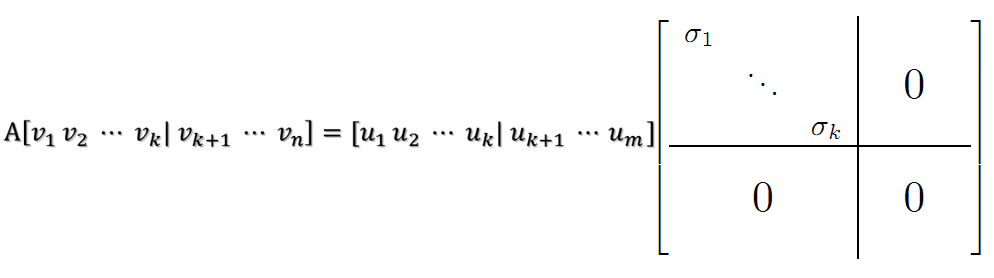
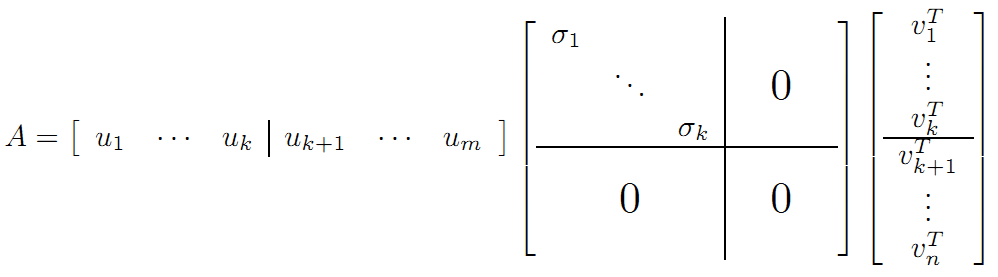
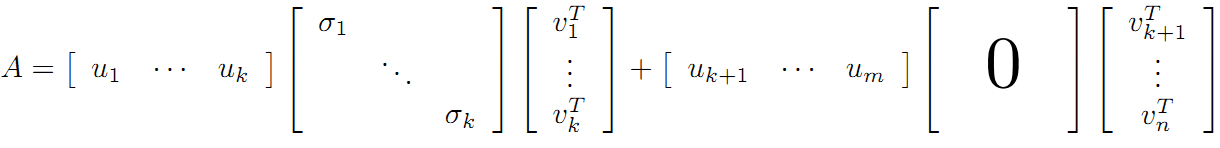

 浙公網(wǎng)安備 33010602011771號
浙公網(wǎng)安備 33010602011771號