數據結構·字符串和圖

1.字符串的存儲

1.1.字符數組和STL`string`

`char s[N]`

strlen(s+i)：$O(n)$。返回從 s[0+i] 開始直到 '\0' 的字符數。
strcmp(s1,s2)：$O(\min(n_1,n_2))$。若 s1 字典序更小返回負值，兩者一樣返回 0，s1 字典序更大返回正值。
strcat(s1,s2)：$O(n_2)$。將s2接到s1的結尾，用*s2替換s1末尾的'\0'返回s1。
s[i]：$O(1)$。訪問s[i]。

不可使用==，不會報錯，但會警告，運行會得到錯誤的結果。

`string s`

s.length()：$O(1)$。返回字符串字符個數。
s1<=>s2：$O(\min(n_1,n_2))$。string重載了比較邏輯運算符。
s1=s1+s2;：$O(n_2)$。將s2接到s1結尾，返回連接后的string。
s[i]：$O(1)$。訪問s[i]。

《C++語言.4.1.字符串 string》

1.2.$Trie$樹

1.2.1.$Trie$樹

int n;
int son[N][26],cnt[N],idx;
char str[N];

void insert(){
    int p=0;
    for(int i=0;str[i];i++){
        int u=str[i]-'a';
        if(!son[p][u]) son[p][u]=++idx;
        p=son[p][u];
    }
    cnt[p]++;
    return ;
}

int query(){
    int p=0;
    for(int i=0;str[i];i++){
        int u=str[i]-'a';
        if(!son[p][u]) return 0;
        p=son[p][u];
    }
    return cnt[p];
}

int main(){
    cin>>n;
    while(n--){
        char op[2];
        scanf("%s%s",op,str);
        if(op[0]=='I'){
            insert();
        }
        else {
            printf("%d\n",query());
        }
    }
    return 0;
}

1.2.2.$01Trie$樹

適用條件：存儲二進制數以得知是否存在某類滿足依次按位要求的數。

代碼類似于《數據結構·字符串和圖1.2.1.Trie樹》，只不過只有0、1兩條字母邊。

1.2.2.1.求$a\operatorname{xor}b_i$的最值

例題。

方法一：$01Trie$樹$O(N\log N)$

優點：復雜度更低。

方法二：$01Trie$思想+值域線段樹$O(N\log^2 N)$

優點：適用范圍廣，可以解決更多的約束條件。

01trie樹的作用：得知是否存在某類滿足依次按位要求的數。值域線段樹也可以做到！

假設當前5位的數已經枚舉了2位10***，現在要枚舉第3位為1，則只需查詢[10100,10111]是否存在數。

從大到小枚舉數的每一位。根據上文，查詢滿足要求的區間是否存在滿足要求的數。然后思想中模擬01Trie樹選擇決策，枚舉下一位。

2.字符串的表示

2.1.字符串$Hash$

《基礎算法6.2.字符串Hash》

基礎算法

2.2.字符串的最小表示法

1個字符串s有$s_{len}$個循環同構（$e.g.$abc：abc、bca、cab），其中字典序最小的一個稱為s的最小表示法。

雙指針算法。

以判定2個字符串是否可以通過循環同構而相等為例：

int len;
char a[N],b[N];

int get_min(char s[])
{
    int i=1,j=2;//錯開i和j
    while(i<=len && j<=len)
    {
        int k=0;
        while(k<len && s[i+k]==s[j+k]) k++;
        if(k==len) break;//說明原串是一個循環串，（假設i<j）s[i..j-1]是循環節。又因為j走過了s[i..j-1]遍歷了整個循環節，所以起點i或j一定是最小表示法
        if(s[i+k]>s[j+k]) i+=k+1;//說明起點[i,i+k]不可能成為最小表示法。證明：對于任意一個起點i'\in[i,i+k]，都可以找到j'=j+(i'-i)，使得s[i'..i+k]>s[j'..j+k]
        else j+=k+1;
        if(i==j) j++;//錯開i和j
    }
    int k=min(i,j);//min：可能其中一個指針走到了盡頭而跳出循環，所以要去除該指針
    s[k+len]=0; //方便下面strcmp判定，注意不要多加1！
    return k;   //從s[k]開始是最小表示
}

int main()
{
    scanf("%s%s",a+1,b+1);
    len=strlen(a+1);
    memcpy(a+1+len,a+1,len);    //破環成鏈
    memcpy(b+1+len,b+1,len);
    int x=get_min(a),y=get_min(b);  //從a[x]開始是最小表示
    if(strcmp(a+x,b+y)) puts("No");
    else
    {
        puts("Yes");
        puts(a+x);
    }
    return 0;
}

3.字符串組前綴問題

$\operatorname{lcp}(s,t)$：字符串s和t的最長公共前綴的長度。

Trie樹
按字典序排序

排序后的性質：
- $\max\limits_{j\in[1,i)\cup(i,n]}\operatorname{lcp}(s_i,s_j)=\max(\operatorname{lcp}(s_i,s_{i-1}),\operatorname{lcp}(s_i,s_{i+1}))$。
- $\operatorname{lcp}(s_i,s_j)=\min\limits_{k\in]i,j]}(\operatorname{lcp}(s_i,s_k),\operatorname{lcp}(s_k,s_j))=\min\limits_{k\in[i,j)}\operatorname{lcp}(s_k,s_{k+1})$。
動態規劃

4.字符串組匹配問題和字符串子串周期問題

4.1.一匹一：KMP算法

4.1.1.KMP$O(N)$

真前綴函數ne[i]=k：對于i最大的$k\in[1,i-1]$使得s[1..k]=s[i-k+1..i]，即s[1..i]的最長公共真前后綴。

下標從1開始。

如果要在字符串后面接字符，KMP可以從新字符開始繼續求出ne。

復雜度分析：i的整個循環中，1.j最多加n次；2.由于第1條且j非負，j最多減n次。故復雜度為$O(N)$。

cin>>n>>p+1>>m>>s+1;
for(int i=2/*真前綴*/,j=0;i<=n;i++){
    while( j && p[i]!=p[j+1]) j=ne[j];
    if(p[i]==p[j+1]) j++;
    ne[i]=j;
}
for(int i=1,j=0;i<=m;i++){
    while( j && s[i]!=p[j+1]) j=ne[j];
    if(s[i]==p[j+1]) j++;
    if(j==n){//P與模版串S中的一個子串匹配成功
        //printf("%d ",i-n);//輸出P在模版串S中作為子串（可以交叉）所有出現的位置的起始下標
        j=ne[j];
    }
}

字符串子串周期問題

類似于KMP，根據周期性和相等區間的傳遞性。

KMP解決最小循環節問題

ans=n-ne[n];
if(n%ans!=0) ans=n;//字符串末尾是不完整的循環節

4.1.2.擴展KMP（Z函數）$O(N)$

下標從1開始。

Z函數：給定長度為n的字符串s，定義一個數組z[]，其中z[i]表示LCP(s[i_n],s[1n])，LCP的意思是最大公共前綴。

l、r：r=l+z[l]-1。l為1~i-1中最大的$r_i$的l。

初始條件：定義z[1]=0（或者根據題意定義為n），l=r=1。

假設已經處理出z[1~i-1]求z[i]。

如果i>r，直接暴力匹配。
如果i≤r，可以利用i'=i-l+1的信息。
- 證明
  
  顯然i>l，所以$i\in(l,r]$。
  
  因為s[l_{r]一定和s[1}r-l+1]相同，為表示方便，設l'=1,r'=r-l+1，所以我們可以找到一個i'=i-l+1，顯然s[i_r]和s[i'r']相同。
1. 如果z[i'] <r-i+1，直接令z[i]=z[i']，并結束這次計算。
  - 證明
    
    假設z[i]>z[i']，又因為s[i_r]和s[i-l+1r-l+1]相同，z[i'] <r-i+1說明z[i']失配是在第r個之前的字符，矛盾。
2. 如果z[i'] ≥r-i+1，先令z[i]=z[i']，由于還沒有掃描到s[r]之后的字符，所以直接繼續暴力匹配。
匹配完i之后，及時更新l和r。

由于r只會增大，所以復雜度是$O(N)$的。

void exkmp(char s[])
{
    int len=strlen(s+1);
    z[1]=len;
    for(int i=2,l=1,r=1;i<=len;i++)
    {
        if(i<=r) z[i]=min(z[i-l+1],r-i+1);
        else z[i]=0;
        while(i+z[i]<=len && s[i+z[i]]==s[1+z[i]]) z[i]++;
        if(i+z[i]-1>=r) l=i,r=i+z[i]-1;
    }
    return ;
}

應用

給定字符串A和B，求B的每個后綴和A匹配的最長長度，即對于每一個$i\in[1,len(B)]$，求出LCP(B[i~len(B)],A)。$O(N+M)$

構造字符串C=A+ch+B，其中ch是一個從未在A,B中出現過的字符，對于每一個$i\in[len(A)+2,len(A)+1+len(B)]$求出$Z_C[i]$即可。
求出A的本質不同的子串個數，并支持操作：在A末尾增加某個字符或刪去尾字符。$O(QN)$

只考慮增加字符。設$s_{bef}$表示增加前的字符串，$s_{aft}$表示增加后的字符串。

把A倒過來，那么原本在末尾增加就是在前面增加。

增加一個字符，就增加$len(s_{bef})$個子串。

因此只要知道新增加的子串有多少個之前已經算過的，就可以計算出有多少個新增加的本質不同子串。對$s_{bef}$跑一遍擴展KMP，找出最大的i≠1的z[i]，那么新增加的子串僅有z[i]個串已經計算過。
給定某個串s，求出它的嚴格循環節。$O(N)$

跑出s的Z函數，若i+z[i]-1=len(s)，且(i-1)|z[i]，則s[1~i-1]就是一個嚴格循環節。

4.2.一匹多：AC自動機

類比KMP。

功能

給定n個串$s_i$和串t，統計每個串$s_i$在串t中的出現次數。

int n;
char s[N];
int pos[N]; //pos[i]：串s_i在AC自動機上的節點編號
int idx;
struct AC
{
    int son[26],fail;   //fail：深度最大的fail使得tr[0->fail]是tr[0->u]的后綴
    int in,f;   //in：入度；f：要求的值，此處是根節點到點u的串在串t中出現了多少次
}tr[N];
int q[N],hh,tt;

//與字典樹插入字符串一模一樣
void insert(int id)
{
    int u=0;
    for(int i=1;s[i];i++)
    {
        int c=s[i]-'a';
        if(!tr[u].son[c]) tr[u].son[c]=++idx;
        u=tr[u].son[c];
    }
    pos[id]=u;
    return ;
}

//建立fail
void build()
{
    hh=1,tt=0;
    for(int c=0;c<26;c++) if(tr[0].son[c]) q[++tt]=tr[0].son[c];
    while(hh<=tt)
    {
        int u=q[hh];
        hh++;
        for(int c=0;c<26;c++)
        {
            //理解：在循環第i層時，前i-1層一定都求對了，tr[tr[u].fail].son[c]是一定正確的，這是一個類路徑壓縮的遞歸的過程
            //后面串t在走的過程中，原串有tr[u].son[c]（匹配）走tr[u].son[c]，沒有tr[u].son[c]（失配）看有沒有tr[tr[u].fail].son[c]
            if(!tr[u].son[c]) tr[u].son[c]=tr[tr[u].fail].son[c];   //失配了，此時應該執行類路徑壓縮，它最終應該跳到的位置是tr[tr[u].fail].son[c]
            else    //匹配，此時應該求出fail并繼續往下走
            {
                //因為串s匹配，串s的后綴也一定匹配，所以建立fail的有向邊：tr[u].son[c]->tr[tr[u].fail].son[c]
                tr[tr[tr[u].fail].son[c]].in++;
                tr[tr[u].son[c]].fail=tr[tr[u].fail].son[c];
                q[++tt]=tr[u].son[c];
            }
        }
    }
    return ;
}

//串t開始匹配s_1,...s_n
/*
正確性：
根據fail的定義，串t在AC自動機上一定盡可能地往深度大的走，利用了盡可能長的后綴的信息。
根據build()，串t在走的過程中，原串有tr[u].son[c]走tr[u].son[c]，沒有tr[u].son[c]看有沒有tr[tr[u].fail].son[c]，這是一個遞歸過程。
所以此時深度更大的節點一定不是t的子串，深度更小的節點（fail的fail）一定是t的子串。
為了保證復雜度，先把貢獻加到t走到的點u，之后拓撲排序再把貢獻加到tr[u].fail。
所以先讓串t沿著AC自動機走并打標記，再拓撲排序一定是正確的。
*/
void solve()
{
    //串t沿著AC自動機走并打標記
    int u=0;
    for(int i=1;s[i];i++)
    {
        int c=s[i]-'a';
        u=tr[u].son[c];
        tr[u].f++;
    }
    
    //拓撲排序，DAG上轉移求出tr[u].f
    hh=1,tt=0;
    for(int u=1;u<=idx;u++) if(!tr[u].in) q[++tt]=u;
    while(hh<=tt)
    {
        int u=q[hh];
        hh++;
        int v=tr[u].fail;
        tr[v].f+=tr[u].f;
        tr[v].in--;
        if(!tr[v].in) q[++tt]=v;
    }
    
    return ;
}

scanf("%d",&n);
for(int i=1;i<=n;i++)
{
    scanf("%s",s+1);
    insert(i);
}
build();
scanf("%s",s+1);
solve();
//此后tr[pos[i]].f=串s_i在t中的出現次數

應用

fail樹

插入AC自動機的字符串x在另外一個插入AC自動機的字符串y中出現了多少次$\Leftrightarrow$從根到y的末尾的路徑上的所有節點中有多少個節點通過fail指針直接或間接指向了x的末尾。

對于fail指針v→u，建立有向邊u→v。顯然會構成一棵有向樹。所以“直接或間接指向”$\Leftrightarrow$“在子樹內”。

注意建邊時要記得給指向點0的fail指針也建邊：從點0向在加入初始隊列時的點建邊。

利用fail樹，將原字符串問題轉化為樹上問題。
AC自動機上dp

5.字符串子串問題

5.1.后綴數組

性質：

設lcp(i,j)表示后綴編號為i和j的最長公共前綴，h(i)表示后綴編號為i的后綴與排名是rk[i]-1的后綴的最長公共前綴。
lcp(i,j)=lcp(j,i)；lcp(i,i)=len(i)；若i和j已經排好序：lcp(i,j)=min(lcp(i,k),lcp(k,j)),(i≤k≤j)。height[i]=lcp(sa[i-1],sa[i])；h(i)=height[rk[i]]；h(i)≥h(i-1)-1；
所有非空后綴的非空前綴集合$\Leftrightarrow$所有非空子串的集合。
先用后綴數組排序，排好序后，所有互不相同的非空子串個數$=\sum\limits_{i=1}^{n} (len_i-height_i)$；
排序后，一個后綴與前面的后綴的最大公共前綴長度$≤height_i$。

下面使用倍增求后綴數組，$O(n\log n)$，常數較小。

int n;
int sa[N],rk[N],height[N];  //sa[i]：排名是i的后綴編號；rk[i]：后綴編號是i的排名；height[i]：排名是i的后綴與排名是i-1的后綴的最長公共前綴
int c[N],sec[N],seidx,Hash[N],hidx,backup[N]; //基數排序的變量。c：桶；sec[i]：按第二關鍵字的排名是i的后綴編號；Hash[i]：后綴編號為i的前k個字符的哈希值
char s[N];

void get_sa()
{
    //先按首字符基數排序
    for(int i=1;i<=n;i++/*編號*/)
    {
        Hash[i]=(int)s[i];
        c[Hash[i]]++;
    }
    for(int i=2;i<=hidx;i++) c[i]+=c[i-1];
    for(int i=n;i>=1;i--/*編號*/) sa[c[Hash[i]]--]=i;
    
    //倍增計算sa
    for(int k=1;k<=n;k<<=1) //第1~k字符是第一關鍵字，第k+1~2k字符是第二關鍵字
    {
        //上一輪k已經求出本輪k<<1前k個字符的哈希值
        
        //按第二關鍵字排序
        seidx=0;
        for(int i=n-k+1;i<=n;i++/*編號*/) sec[++seidx]=i;   //第二關鍵字為空的情況
        for(int i=1;i<=n;i++/*排名*/) if(sa[i]>k) sec[++seidx]=sa[i]-k; //這里借助了循環sa和++seidx來確定相對排名，后綴編號為sa[i]-k的第二關鍵字的相對排名等于上一輪k的后綴編號為sa[i]的相對排名
        
        //最終seidx=n
        //按第一關鍵字排序
        for(int i=1;i<=hidx;i++) c[i]=0;    //注意別忘了初始化桶
        for(int i=1;i<=seidx;i++/*編號*/) c[Hash[sec[i]]]++;//注意這里可不帶sec[]
        for(int i=2;i<=hidx;i++) c[i]+=c[i-1];
        for(int i=seidx;i>=1;i--/*第二關鍵字排名*/) sa[c[Hash[sec[i]]]--]=sec[i];    //注意這里要帶個sec[i]
        
        //開始計算下一輪k<<2后綴編號為i的前k<<1個字符的哈希值
        memcpy(backup,Hash,sizeof backup);
        Hash[sa[1]]=1,hidx=1;
        for(int i=2;i<=n;i++/*排名*/) Hash[sa[i]]= (backup[sa[i]]==backup[sa[i-1]]/*前k個字符相等*/ && backup[sa[i]+k]==backup[sa[i-1]+k]/*后k個字符相等*/) ? hidx : ++hidx;
        if(hidx==n) return ;    //排名完成
    }
    
    return ;
}

void get_height()
{
    //求rk數組
    for(int i=1;i<=n;i++/*排名*/) rk[sa[i]]=i;
    
    //利用h[i]>=h[i-1]-1求height數組
    for(int i=1,k=0;i<=n;i++/*編號*/)
    {
        if(rk[i]==1) continue;
        if(k) k--;  //運用了上一輪的信息
        int j=sa[rk[i]-1];
        while(i+k<=n && j+k<=n && s[i+k]==s[j+k]) k++;
        height[rk[i]]=k;    //注意這里別忘了帶rk[]
    }
    
    return ;
}

int main()
{
    scanf("%s",s+1);
    n=strlen(s+1);
    hidx=(int)'z';
    get_sa();
    get_height();
    for(int i=1;i<=n;i++/*排名*/) printf("%d ",sa[i]);
    puts("");
    for(int i=1;i<=n;i++/*排名*/) printf("%d ",height[i]);
    puts("");
    return 0;
}

例題1：動態統計所有互不相同的非空子串個數

S最初為空串，每次向S的結尾加入一個字符，并求出此時S中所有互不相同的非空子串的個數。

后綴數組的性質：
1. 設lcp(i,j)表示后綴編號為i和j的最長公共前綴，h(i)表示后綴編號為i的后綴與排名是rk[i]-1的后綴的最長公共前綴。
  若i和j已經排好序：lcp(i,j)=min(lcp(i,k),lcp(k,j)),(i≤k≤j)；
2. 所有后綴的前綴集合$\Leftrightarrow$所有子串的集合。
  先用后綴數組排序，排好序后，所有互不相同的子串個數$=\sum\limits_{i=1}^{n} (len_i-height_i)$；
3. 排序后，一個后綴與前面的后綴的最大公共前綴長度$≤height_i$。
所有互不相同的子串個數$=\sum\limits_{i=1}^{n} (len_i-height_i)$。

每次插入1個數都會改變所有的后綴，麻煩！我們逆向思考：開始給定一個“逆”串，每次刪除1個首字符，這樣只會刪除1個后綴。由lcp(i,j)=min(lcp(i,k),lcp(k,j)),(i≤k≤j)，相當于答案：

res-=(n-sa[k]+1)-height[k];
res-=(n-sa[j]+1)-height[j];
height[j]=min(height[j],height[k]);
res+=(n-sa[j]+1)-height[j];

#include<bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N=1e5+5;
int n;
int s[N];
int sa[N],rk[N],height[N];
int c[N],sec[N],sidx,h[N],hidx,backup[N];
int l[N],r[N];
LL ans[N],res;
unordered_map<int,int> ha;

int Hash(int x)
{
    if(ha.count(x)==0) ha[x]=++hidx;
    return ha[x];
}

void get_sa()
{
    for(int i=1;i<=n;i++)
    {
        h[i]=s[i];
        c[h[i]]++;
    }
    for(int i=2;i<=hidx;i++) c[i]+=c[i-1];
    for(int i=n;i>=1;i--) sa[c[h[i]]--]=i;
    
    for(int k=1;k<=n;k<<=1)
    {
        sidx=0;
        for(int i=n-k+1;i<=n;i++) sec[++sidx]=i;
        for(int i=1;i<=n;i++) if(sa[i]>k) sec[++sidx]=sa[i]-k;
        
        for(int i=1;i<=hidx;i++) c[i]=0;
        for(int i=1;i<=sidx;i++) c[h[sec[i]]]++;
        for(int i=2;i<=hidx;i++) c[i]+=c[i-1];
        for(int i=sidx;i>=1;i--) sa[c[h[sec[i]]]--]=sec[i];
        
        memcpy(backup,h,sizeof backup);
        h[sa[1]]=1,hidx=1;
        for(int i=2;i<=n;i++) h[sa[i]]= (backup[sa[i]]==backup[sa[i-1]] && backup[sa[i]+k]==backup[sa[i-1]+k]) ? hidx : ++hidx;
        if(hidx==n) return ;
    }
    
    return ;
}

void get_height()
{
    for(int i=1;i<=n;i++) rk[sa[i]]=i;
    
    for(int i=1,k=0;i<=n;i++)
    {
        if(rk[i]==1) continue;
        if(k) k--;
        int j=sa[rk[i]-1];
        while(i+k<=n && j+k<=n && s[i+k]==s[j+k]) k++;
        height[rk[i]]=k;
    }
    
    return ;
}

int main()
{
    scanf("%d",&n);
    for(int i=n;i>=1;i--) scanf("%d",&s[i]),s[i]=Hash(s[i]);
    get_sa();
    get_height();
    for(int i=1;i<=n;i++)
    {
        res+=(n-sa[i]+1)-height[i];
        l[i]=i-1,r[i]=i+1;
    }
    l[n+1]=n,r[0]=1;
    for(int i=1;i<=n;i++)
    {
        ans[i]=res;
        int k=rk[i],j=r[k];
        res-=(n-sa[k]+1)-height[k];
        res-=(n-sa[j]+1)-height[j];
        height[j]=min(height[j],height[k]);
        res+=(n-sa[j]+1)-height[j];
        r[l[k]]=r[k],l[r[k]]=l[k];
    }
    for(int i=n;i>=1;i--) printf("%lld\n",ans[i]);
    return 0;
}

5.2.后綴自動機

解決的問題：子串問題。

一、SAM的構造過程extend

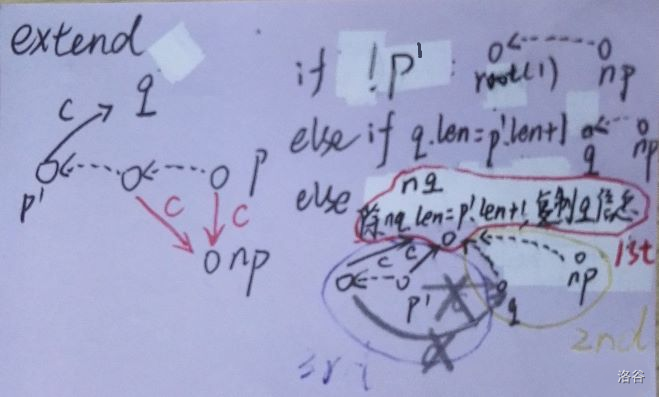
通過這樣的構造過程，可以保證下面的性質全部成立！

包括但不限于：當多個字符串的endpos集合完全相同時，稱他們為同一個等價類。每一個等價類與后綴自動機的一個點一一對應，同一個等價類都在后綴自動機的同一個點，后綴自動機的每一個點只對應一個等價類，且所有的點恰好完全覆蓋所有等價類。

二、SAM的性質:

SAM是個狀態機。一個起點，若干終點。原串的所有子串和從SAM起點開始的所有路徑一一對應，不重不漏。所以終點就是包含后綴的點。
每個點包含若干子串，每個子串都一一對應一條從起點到該點的路徑。且這些子串一定是里面最長子串的連續后綴。
SAM問題中經常考慮兩種邊：
(1) 普通邊，類似于Trie。表示在某個狀態所表示的所有子串的后面添加一個字符。
(2) Link、Father。表示將某個狀態所表示的最短子串的首字母刪除。這類邊構成一棵樹。

后綴自動機的點數最多2N，邊數最多3N。
三、SAM的構造思路及endpos的性質

endpos(s)：子串s所有出現的位置（尾字母下標）集合。SAM中的每個狀態都一一對應一個endpos的等價類。
endpos的性質：
(1) 令 s1,s2 為 S 的兩個子串，不妨設 |s1|≤|s2| （我們用 |s| 表示 s 的長度，此處等價于 s1 不長于 s2 ）。則 s1 是 s2 的后綴當且僅當 endpos(s1)?endpos(s2) ，s1 不是 s2 的后綴當且僅當 endpos(s1)∩endpos(s2)=?　。
(2) 兩個不同子串的endpos，要么有包含關系，要么沒有交集。
(3) 兩個子串的endpos相同，那么短串為長串的后綴。
(4) 對于一個狀態 st ，以及任意的 longest(st) 的后綴 s ，如果 s 的長度滿足：|shortest(st)|≤|s|≤|longsest(st)| ，那么 s∈substrings(st) 。

后綴自動機的點數最多2N，邊數最多3N。
因為同一個等價類中的所有子串一定是里面最長子串的連續后綴，所以后綴自動機每一個點（同一個等價類）代表的不同字串個數=$i_{len_{max}}$$-$$i_{len_{min}}$$+1$，其中$i_{len_{min}}=fa_{len_{max}}+1$；
注意建邊的方向e.g. 1->z->yz\xyz\wxyz->...vwxyz...

功能

求不同子串的數量。
判斷一個字符串是否是某個子串，如果是求某它出現的次數。
求多個最長公共子串。（思想類似于KMP移動“指針”）

復雜度

若字符集大小$|\Sigma|$可看作常數，則時空復雜度是$O(n)$。

否則，從一個結點出發的轉移需要存儲在支持快速查詢和插入的平衡樹中，時間復雜度是$O(n\log|\Sigma|)$，空間復雜度是$O(n)$。

C++代碼

//同一個等價類都在后綴自動機的同一個點，后綴自動機的每一個點只對應一個等價類，且所有的點恰好完全覆蓋所有等價類！！！
int res;
char str[N],query[N];

int tot=1,last=1;   //1是起點（代表的字符為空）
struct Node
{
    int len,fa; //len：最長長度
    int ch[26];
}node[N*2];
int h[N*3],e[N*3],ne[N*3],idx;    //fa邊的dfs遍歷統計信息

int f[N*2];    //f[i]：endpos[i]的大小，i為一個等價類對應的后綴自動機的點
int now[N*2],ans[N*2];  //now：當前字符串與第一個字符串的最長公共子串；ans：所有字符串的最長公共子串

void extend(int c)
{
    int p=last,np=last=++tot;
    f[np]=1;
    node[np].len=node[p].len+1;
    for(;p && !node[p].ch[c];p=node[p].fa) node[p].ch[c]=np;
    if(!p) node[np].fa=1;
    else
    {
        int q=node[p].ch[c];
        if(node[q].len==node[p].len+1) node[np].fa=q;
        else
        {
            int nq=++tot;
            node[nq]=node[q],node[nq].len=node[p].len+1;
            node[np].fa=node[q].fa=nq;
            for(;p && node[p].ch[c]==q;p=node[p].fa) node[p].ch[c]=nq;
        }
    }
    return ;
}

void add(int u,int v)
{
    e[++idx]=v;
    ne[idx]=h[u];
    h[u]=idx;
    return ;
}
//e.g.  1->z->yz\xyz\wxyz->...vwxyz\...

//計算出endpose[i]的大小
void dfs(int u)
{
    for(int i=h[u];i!=0;i=ne[i])
    {
        dfs(e[i]);
        f[u]+=f[e[i]];  //節點u所代表的等價類中的所有整個字符串，肯定是e[i]中等價類中的所有字符串的子串
    }
    return ;
}

int find()
{
    int p=1;
    for(int i=0;query[i];i++)
    {
        int c=query[i]-'a';
        if(node[p].ch[c]) p=node[p].ch[c];
        else return -1;
    }
    return p;
}

void dfs2(int u)
{
    for(int i=h[u];i!=0;i=ne[i])
    {
        dfs2(e[i]);
        now[u]=max(now[u],now[e[i]]);
    }
    return ;
}

int main()
{
    //建立后綴自動機
    scanf("%s",str);
    for(int i=0;str[i];i++) extend(str[i]-'a');
    for(int i=2;i<=tot;i++) add(node[i].fa,i);  //注意方向
    
    //功能1：求不同子串的數量
    res=0;
    for(int i=1;i<=tot;i++) res+=node[i].len-(node[node[i].fa].len+1)+1;    //后綴自動機的每個節點能表示的字符串數=i_{len_{max}}-i_{len_{min}}+1，其中i_{len_{min}}=fa_{len_{max}}+1
    printf("%d\n",res);
    
    //功能2：判斷一個字符串是否是某個子串，如果是求某它出現的次數
    dfs(1);//計算出endpose[i]的大小
    scanf("%s",query);
    res=find(); //這個子串的邊界就是find()。沿著路徑找就可以，別把問題想復雜
    if(res==-1) puts("-1");
    else printf("%d\n",f[res]);
    
    //功能3：求多個最長公共子串
    int q;
    scanf("%d",&q);
    for(int i=1;i<=tot;i++) ans[i]=node[i].len;
    for(int i=1;i<=q;i++)
    {
        memset(now,0,sizeof now);
        scanf("%s",query);
        int p=1;
        res=0;
        for(int j=0;query[j];j++)
        {
            int c=query[j]-'a';
            while(p>1 && !node[p].ch[c])//！！！關鍵之處！！！
            {
                p=node[p].fa;
                res=node[p].len;//注意不是在循環外面執行該行代碼。因為len表示等價類的最長長度。
            }
            if(node[p].ch[c]) p=node[p].ch[c],res++;
            now[p]=max(now[p],res);
        }
        dfs2(1);
        for(int j=1;j<=tot;j++) ans[j]=min(ans[j],now[j]);
    }
    res=0;
    for(int i=1;i<=tot;i++) res=max(res,ans[i]);
    printf("%d\n",res);
    
    return 0;
}

6.字符串回文子串問題

6.1.manacher算法 $O(n)$

先將原串每個字符間插入特殊字符，兩邊插入不同特殊字符哨兵。$e.g.$abaabaaba→$#a#b#a#a#b#a#a#b#a#^。循環時借助之前信息跳，再向兩邊拓展，得到數組p[i]：在新串中以str[i]為中心最大回文串的半徑（長度為1的回文串的半徑為1）。最后在原串中每個回文子串的長度=p[i]-1。

int len,ans;
char s[N],str[N*2];//s：原串；str：新串（注意開2倍）
int p[N*2];//p[i]：以str[i]為中心最大回文串的半徑

void init()//建立新串
{
    str[len]='$';//哨兵
    str[++len]='#';
    for(int i=0;s[i];i++) str[++len]=s[i],str[++len]='#';
    str[++len]='^';//哨兵
    return ;
}

void manacher()
{
    int mid,rmax=0;//已知rmax最大的回文字符串[mid*2-rmax,rmax]的信息
    for(int i=1;i<len;i++)
    {
        if(i<rmax) p[i]=min(p[mid*2-i],rmax-i+1);//mid*2-i：i關于mid的對稱點
        else p[i]=1;
        
        while(str[i-p[i]]==str[i+p[i]]) p[i]++;//向兩邊擴展
        
        if(i+p[i]-1>=rmax)
        {
            rmax=i+p[i]-1;
            mid=i;
        }
    }
    return ;
}

scanf("%s",s);
init();
manacher();
for(int i=1;i<len;i++) ans=max(ans,p[i]);
printf("%d\n",ans-1);//注意最后減1

6.2.hash $O(nlogn)$

int n,c;
ULL h1[N],h2[N],q[N];
char str[N];

ULL get(ULL h[],int l,int r){
    return h[r]-h[l-1]*q[r-l+1];
}

int main(){
    while(scanf("%s",str+1),str[1]!='E'){
        n=strlen(str+1);
        n<<=1;
        for(int i=n;i!=0;i-=2){
            str[i]=str[i>>1];
            str[i-1]='a'+26;
        }
        q[0]=1;
        for(int i=1,j=n;i<=n;i++,j--){
            h1[i]=h1[i-1]*mo+str[i]-'a'+1;
            h2[i]=h2[i-1]*mo+str[j]-'a'+1;
            q[i]=q[i-1]*mo;
        }
        int res=0;
        for(int i=1;i<=n;i++){
            int l=0,r=min(i-1,n-i);
            while(l<r){
                int mid=(l+r+1)>>1;
                if(get(h1,i-mid,i-1)!=get(h2,n-(i+mid)+1,n-(i+1)+1)) r=mid-1;
                else l=mid;
            }
            if(str[i-l]<='z') res=max(res,l+1);
            else res=max(res,l);
        }
        printf("Case %d: %d\n",++c,res);
    }
    return 0;
}

6.3.dp$O(N^2)$

適用條件：有約束條件。

區間dp：$f_{len,i}$：長度為len，以s[i]為第一個字符的字符串是否為回文串。

轉移：$f_{len,i}=\begin{cases}f_{len-2,i+1}&s[i]==s[i+len-1]\\\text{false}&s[i]\not=s[i+len-1]\end{cases}$。

邊界：$f_{0,i}=f_{1,i}=\text{true}$。

7.鄰接表

樹與圖的一種存儲方式。

int h[N],e[M],w[M],ne[M],idx;

void add(int u,int v,int wor){
    //idx：邊的編號
    e[++idx]=v;   //e：編號為idx的邊所指向的終點
    w[idx]=wor;   //w：編號為idx的邊的權值
    ne[idx]=h[u];   //ne：以head為起點，編號為idx的邊的下一條邊
    h[u]=idx;   //h：以點a為起點，最后一條邊的編號
    return ;
}

//初始化
idx=0;
memset(h,0,sizeof h);

//遍歷每條邊且要知道起終點
for(int u=1;u<=n;u++)
    for(int i=h[u];i!=0;i=ne[i])
        cout<<u<<' '<<e[i]<<' '<<w[i]<<endl;

8.并查集（無向圖的連通性、動態維護傳遞性關系）

8.1.并查集的優化方式

8.1.1.路徑壓縮并查集

int fa[N];

//初始化，不要忘記！！！
for(int i=1;i<=n;i++) fa[i]=i;

//find
int find(int x)
{
    if(x!=fa[x]) fa[x]=find(fa[x]);
    return fa[x];
}

//find：涉及到合并信息
int find(int x)
{
    if(x!=fa[x]){
        //注意下面的順序
        int root=find(fa[x]);
        dis[x]+=dis[fa[x]];
        fa[x]=root;
    }
    return fa[x];
}
for(int i=1;i<=n;i++) dis[i]=1;

//merge
//注意，并查集大小可以不在路徑壓縮時更新
siz[find(y)]+=siz[find(x)];
fa[find(x)]=find(y);

//并查集的換根操作
//并查集不支持刪除根節點的操作，但是并查集中多余了一個點不會影響其他點，因此我們令原根節點指向新根節點，新根節點指向自己
p[rt]=new_rt,p[new_rt]=new_rt;

8.1.2.按秩合并并查集

秩dep[i]：當i作為根節點時，它到葉子節點的距離。只有根節點的秩對于復雜度有意義。

按秩合并：每次合并時令秩大的并查集是秩小的并查集的父親，盡量不改變秩的大小。但是當兩個并查集的秩的大小一樣時，其中被令為另一個并查集的父親的并查集的秩的大小要改變+1。

int p[N],dep[N];

//初始化，不要忘記！！！
for(int i=1;i<=n;i++) p[i]=i；

//find
int find(int x)
{
    while(x!=p[x]) x=p[x];
    return x;
}

//merge
void merge(int x,int y)
{
    x=find(x),y=find(y);
    if(x==y) return ;
    if(dep[x]>dep[y]) swap(x,y);    //按秩合并，每次合并時令秩大的并查集是秩小的并查集的父親，盡量不改變秩的大小
    p[x]=y;
    if(dep[x]==dep[y]) dep[y]++;    //當原先x、y秩的大小一樣，現令y是x的父親時，y的秩的大小改變+1
    return ;
}

8.2.并查集的拓展方式

8.2.1.“擴展域”并查集（思路更簡潔，但是空間更大）

$x$是同類域；$x+n$是敵人域……

8.2.2.“邊帶權”并查集

2種關系→異或：路徑壓縮時，對x到樹根路徑上的所有邊權做異或運算，即可得到x與樹根的奇偶性關系：d[x]為0 <-> x與樹根奇偶性相同。如果x與y在同一個集合，若(d[l]^{d[r])!=flag即x與y關系與回答矛盾，小A撒謊；不在同一個集合，則合并兩個集合，令d[fl]=d[l]}d[r]^flag（使連接滿足x、y之間新奇偶關系）。

3種關系→對3取模：

int find(int x){
    if(x!=fa[x]){
        //注意下面的順序
        int root=find(fa[x]);
        dis[x]+=dis[fa[x]];
        fa[x]=root;
    }
    return fa[x];
}

int fx=find(x),fy=find(y);
if(d==1){   //X與Y互為同類域
    if(fx==fy){ //此處不可以寫成fx==fy && (dis[x]-dis[y])%3!=0，否則下面的else判斷條件會出問題
        if((dis[x]-dis[y])%3!=0){   //如果X與Y不互為同類域，矛盾，假話
            ans++;
            continue;
        }
    }
    else{
        fa[fx]=fy;
        dis[fx]=dis[y]-dis[x];
    }
}
else{   //Y的天敵域有x，x的捕食域有y
    if(fx==fy){ 
        if((dis[x]-dis[y]-1)%3!=0)   //如果Y的天敵域沒有x，x的捕食域沒有y，矛盾，假話
        ans++;
        continue;
    }
    else{
        fa[fx]=fy;
        dis[fx]=dis[y]-dis[x]+1;
    }
}

9.樹上問題

9.1.樹上莫隊

數據結構·序列

9.2. 樹上分治算法

非常適合求解與無根樹統計信息相關的內容。

但是樹的形態不能改變，否則使用LCT。

9.2.1.點分治

思考暴力枚舉根節點依次遍歷整棵樹怎么解決原問題。
當前層，找重心u。（達到分治效果保證層數復雜度$O(\log N)$層）
以u為根，直接$O(F_1(N))$暴力遍歷u的每棵子樹統計信息（如果后面合并信息是把信息放到一起雙指針，此時遍歷完一棵子樹后要容斥減去兩端在同一子樹的方案）。
遍歷完所有的子樹后$O(F_2(N))$合并信息：以點u為根……/經過點u的路徑……，貢獻到答案。

所有的方案只有三種情況：
- 子樹內部：遞歸求解。
- 跨子樹（兩端在不同子樹）
  - 方法一：把信息放到一起，排序，雙指針。缺點是可能會出現兩端在同一子樹的方案，需要此時遍歷完一棵子樹后容斥減去。優點是雙指針使得多組詢問復雜度是$O((N\log N+QN)\log N)$。
    
    任意兩點的方案-兩端在同一子樹的方案。
    
    任意兩點的計算：拆成兩個一端到當前重心的路徑。
    
    若計算時，一端不動一端動，則不動的一端到當前重心的路徑的計算=動的一端的個數*不動的一段到當前重心路徑的值。
  - 方法二：每次遍歷完一棵子樹后，子樹向點u合并信息。優點是不需要容斥。缺點是不能套用雙指針，多組詢問復雜度是$O((N\log N+QN\log N)\log N)$。
    
    方案+=一端在舊子樹的方案*一端在新子樹的方案。
- 其中一端是重心：特殊求解（一般利用前面的信息加個特判即可）
刪除重心u（給重心u打標記），遞歸到點u的每棵子樹繼續求解。

雖然每一層都直接$O(F_1(N))$暴力遍歷整棵樹以及$O(F_2(N))$合并信息，但是一共只有$O(\log N)$層。因此總的復雜度是$O((F_1(N)+F_2(N))\log N)$。

距離一般定義為到當前層重心的距離。

bool vis[N];    //刪除標記
int qidx,sidx;
Node q[N],subq[N];//q：當前重心合并的信息；subq：子樹統計的信息

//求u所在的子樹大小
int get_size(int u,int fa)
{
    int siz=1;
    for(int i=h[u];i!=0;i=ne[i])
    {
        int v=e[i];
        if(v==fa || vis[v]/*防止越過該子樹根節點，只遍歷當前子樹*/) continue;
        siz+=get_size(v,u);
    }
    return siz;
}

//求u所在的子樹重心
int get_wc(int u,int fa,int tot,int &wc)
{
    int siz=1,res=0;    //siz：以u為根的樹 的節點數（包括u）；res：刪掉某個節點之后，最大的連通子圖節點數
    for(int i=h[u];i!=0;i=ne[i])
    {
        int v=e[i];
        if(v==fa || vis[v]) continue;
        int son_size=get_wc(v,u,tot,wc);    //子樹v的節點數
        siz+=son_size;  //統計以u為根的樹 的節點數
        res=max(res,son_size);  //記錄最大連通子圖的節點數
    }
    res=max(res,tot-siz);   //選擇u節點為重心，最大的 連通子圖節點數
    if(res<=tot/2) wc=u;    //只要res<=tot/2，就達到了分治的目的，可以狹義理解u就是重心
    return siz;
}

//統計信息，儲存在subq里
void dfs(int u,int fa,int dis)

//合并信息，貢獻到答案。
void solve(int x[],int up,int sign)

//分治主體
void divide(int u)
{
    //當前層，找重心u
    get_wc(u,-1,get_size(u,-1),u);
    
    qidx=0;//記得到達新的重心后清空
    //以u為根，直接O(F_1(N))暴力遍歷u的每棵子樹統計信息
    for(int i=h[u];i!=0;i=ne[i])
    {
        int v=e[i];
        if(vis[v]) continue;
        sidx=0;//記得統計完一棵子樹后要清空
        dfs(v,u);
        //solve(s,sidx,-1);//如果后面合并信息是把信息放到一起，排序，雙指針，則此時需要遍歷完一棵子樹后容斥減去兩端在同一子樹的方案
        for(int i=1;i<=sidx;i++) q[++qidx]=subq[i];
    }
    
    //遍歷完所有的子樹后O(F_2(N))合并信息：以點u為根……/經過點u的路徑……，貢獻到答案
    solve(q,qidx,1);
    
    //刪除重心u（給重心u打標記），遞歸到點u的每棵子樹繼續求解
    vis[u]=true;
    for(int i=h[u];i!=0;i=ne[i])
    {
        int v=e[i];
        if(vis[v]) continue;
        divide(v);
    }
    
    return ;
}

divide(1);

例題1：AcWing 252. 樹

例題2：AcWing 264. 權值

常用技巧

單調隊列按秩合并

求長度為[l,r]的路徑的權值最大值：子樹依次向重心合并信息到桶maxw[dis]：長度為dis的路徑的權值最大值。正在遍歷一棵子樹時中的路徑dis需要在已合并信息的子樹中查找長度為[l-dis,r-dis]的路徑的權值最大值，并與之配對形成跨子樹路徑更新答案。使用bfs+單調隊列可以做到線性。

但是如果以任意順序遍歷子樹，單調隊列的初始化的復雜度是假的（$e.g.$假設R特別大，遍歷的第一棵子樹的深度也特別大，那么在遍歷剩余子樹前單調隊列的初始化的復雜度都是一次$O(N)$，總共$O(N^2)$。）。如果按照子樹內節點的最大深度從小到大的順序遍歷子樹，總的復雜度是$O(\sum dep_{max})=O(N)$。

9.2.2.動態點分治（點分樹）

適用條件：多組詢問的點分治，每個詢問的根節點不同。或者是在線修改的點分治。點分治的結構不變（樹的形態不變）。

若樹的形態改變，則使用LCT。

預處理

點分治。

在divide()中的get_dis(v,fa,wc,dis)中記錄子樹的祖先（當前的重心）和子孫（子樹）的信息。

struct Father
{
    int u,id;//u：祖先節點的編號；id：u在祖先節點的哪棵子樹
    LL dis;//u到祖先的距離
};
vector<Father> fa[N];//fa[u]：u的各個祖先的信息
struct Son
{
    LL dis;//u到子孫的距離
};
vector<vector<son>> son[N];//son[u][id]：u的第id棵子樹中各個子孫的信息

//在divide()中的get_dis(v,fa,wc,dis)中記錄子樹的祖先（當前的重心）和子孫（子樹）的信息。
void get_dis(int u,int father,int wc,int id,int dis)
{
    if(vis[u]) return ;
    fa[u].push_back({wc,id,dis});
    son[wc][id].push_back(dis);
    for(int i=h[u];i!=0;i=ne[i])
    {
        int v=e[i];
        if(v==father) continue;
        get_dis(v,u,wc,id,dis+w[i]);
    }
    return ;
}

void divide(int u)
{
    if(vis[u]) return ;
    get_wc(u,-1,get_size(u,-1),u);
    vis[u]=true;
    for(int i=h[u],id=0;i!=0;i=ne[i])   //id：第id棵子樹
    {
        int v=e[i];
        if(vis[v]) continue;
        get_dis(v,-1,u,id,w[i]);
        //abaabaaba
        id++;//注意不可以放在上面，因為有些v會continue掉
    }
    for(int i=h[u];i!=0;i=ne[i]) divide(e[i]);
    return ;
}

詢問

貢獻分成在u的子樹的和不在u子樹的（也就是祖先和祖先的非u所在子樹的子樹）。

對于不在u子樹的，遍歷u的祖先和祖先的非u所在子樹的子樹。利用fa[u]和son[fa[u]]計算。

對于在u子樹的，遍歷u的子樹。利用son[u]計算。

int query(int u,int l,int r)
{
    int res=0;

    //對于不在u子樹的，遍歷u的祖先和祖先的非u所在子樹的子樹
    for(auto it1 : fa[u])
    {
        res+=calc1(it1.u);    //特判計算重心
        for(int i=0;son[it1.u][i].size()!=0/*祖先有第i棵子樹*/;i++)
        {
            if(i==it1.id) continue;//遍歷祖先的非u所在子樹的子樹
            for(auto it2 : son[it1.u][i]) res+=calc2(it2);
        }
    }
    
    //對于在u子樹的，遍歷u的子樹
    for(int i=0;son[u][i].size()!=0;i++) for(auto it2 : son[u][i]) res+=calc2(it2);
    
    return res;
}

9.3.樹鏈剖分

9.3.1.重鏈剖分

模板題

https://questoj.cn/problem/2251

如果題目是所有區間操作結束后再進行詢問，請考慮$O(N)$的樹上差分而不是復雜度又高代碼又長的樹剖。

樹鏈剖分：適用于路徑、子樹、鄰域的修改和查詢。

歐拉路徑：適用于靜態莫隊算法，不能用于修改。

注意：只有在線段樹上時才采用dfs序編號cnt，其余時候（比如說lca）采用原編號u。

名詞

dfs序：優先遍歷重兒子，即可保證重鏈上所有點的編號是連續的

定理：樹上任意一條路徑均可拆分成$O(\log n)$條重鏈（區間）。

預處理

dfs1：預處理所有節點的重兒子、父節點、深度以及子樹內節點的數量。

dfs2：樹鏈剖分，找出每個節點所屬重鏈的頂點，dfs序的編號（而不是每個點屬于哪條重鏈，用重鏈的頂點來辨別兩點是否在同一重鏈上），并建立 u 到 id 的 w 映射。

路徑→$O(\log n)$條重鏈（區間）

通過重鏈向上爬，找到最近公共重鏈，最后加上在相同重鏈里的區間部分。

子樹→1個區間

以u為根的子樹：[dfn[u],dfn[u]+siz[u]-1]。

鄰域

直接修改/查詢父親和重兒子。

對于輕兒子，它一定是鏈頂節點：

對于修改，在該點打上懶標記，表示該點的輕兒子待修改。在后面的查詢中，鏈頂節點結合其父親的懶標記，額外單點查詢。

對于查詢，在前面的修改中，鏈頂節點額外更新其父親的信息。

代碼

int n,m;
int w[N];
int h[N],e[M],ne[M],idx;

//第一次dfs：預處理
int dep[N],siz[N],fa[N],son[N];  //以原編號u作為編號。dep：深度；siz:子樹節點個數；fa:父節點；son:重兒子

//第二次dfs：做剖分
int top[N]; //以原編號u作為編號。top:重鏈的頂點；
int dfn[N],nw[N],num;    //以dfs序num作為編號。dfn:節點的dfs序編號（時間戳）；nw[dfn[i]]：w->nw的映射

struct Tree
{
    int l,r;
    LL sum,add;
}tr[N*4];

void add_edge(int u,int v)
{
    e[++idx]=v;
    ne[idx]=h[u];
    h[u]=idx;
    return ;
}

//預處理
void dfs1(int u)
{
    dep[u]=dep[fa[u]]+1,siz[u]=1;
    for(int i=h[u];i!=0;i=ne[i])
    {
        int v=e[i];
        if(v==fa[u]) continue;
        fa[v]=u;
        dfs1(v);
        siz[u]+=siz[v];
        if(siz[son[u]]<siz[v]) son[u]=v;    //重兒子是子樹節點最多的兒子
    }
    return ;
}

//做剖分（t是重鏈的頂點）
void dfs2(int u,int t)
{
    dfn[u]=++num,nw[num]=w[u],top[u]=t;
    
    //重兒子重鏈剖分
    if(son[u]==0) return ;
    dfs2(son[u],t);
    
    //輕兒子重鏈剖分
    for(int i=h[u];i!=0;i=ne[i])
    {
        int v=e[i];
        if(v==fa[u] || v==son[u]) continue;
        dfs2(v,v);  //輕兒子的重鏈頂點就是他自己
    }
    
    return ;
}

void eval(int u,LL add)
{
    tr[u].sum+=add*(tr[u].r-tr[u].l+1);
    tr[u].add+=add;
    return ;
}

void pushup(int u)
{
    tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
    return ;
}

void pushdown(int u)
{
    eval(u<<1,tr[u].add);
    eval(u<<1|1,tr[u].add);
    tr[u].add=0;
    return ;
}

void build(int u,int l,int r)
{
    tr[u]={l,r,nw[r],0};
    if(l==r) return ;
    int mid=(l+r)>>1;
    build(u<<1,l,mid),build(u<<1|1,mid+1,r);
    pushup(u);
    return ;
}

void modify(int u,int l,int r,LL add)
{
    if(l<=tr[u].l && tr[u].r<=r)
    {
        eval(u,add);
        return ;
    }
    pushdown(u);
    int mid=(tr[u].l+tr[u].r)>>1;
    if(l<=mid) modify(u<<1,l,r,add);
    if(r>mid) modify(u<<1|1,l,r,add);
    pushup(u);
    return ;
}

LL query(int u,int l,int r)
{
    if(l<=tr[u].l && tr[u].r<=r) return tr[u].sum;
    pushdown(u);
    int mid=(tr[u].l+tr[u].r)>>1;
    LL res=0;
    if(l<=mid) res+=query(u<<1,l,r);
    if(r>mid) res+=query(u<<1|1,l,r);
    return res;
}

//類lca思想，將樹上序列轉化為區間序列
void modify_path(int u,int v,LL add){
    while(top[u]!=top[v])   //向上爬找到相同重鏈
    {
        if(dep[top[u]]<dep[top[v]]) swap(u,v);  //注意不是比較u和v的depth
        modify(1,dfn[top[u]],dfn[u],add); //dfs序原因，上面節點的dfn必然小于下面節點的dfn
        u=fa[top[u]];   //爬到上面一條重鏈
    }
    if(dep[u]<dep[v]) swap(u,v);
    modify(1,dfn[v],dfn[u],add);  //在同一重鏈中，處理剩余區間
    return ;
}

void modify_tree(int u,LL add)
{
    modify(1,dfn[u],dfn[u]+siz[u]-1,add); //由于dfs序的原因，可以利用子樹節點個數直接找到區間，注意不是dfn[u+siz[u]-1]
    return ;
}

//詢問路徑的滿足交換律的信息
LL query_path(int u,int v)
{
    LL res=0;
    while(top[u]!=top[v])
    {
        if(dep[top[u]]<dep[top[v]]) swap(u,v);
        res+=query(1,dfn[top[u]],dfn[u]);
        u=fa[top[u]];
    }
    if(dep[u]<dep[v]) swap(u,v);
    res+=query(1,dfn[v],dfn[u]);
    return res;
}

//詢問路徑的不滿足交換律的信息
Type query_path(int u,int v)
{
    vector<pii> qu,qv;
    bool swa=false;
    while(top[u]!=top[v])
    {
        if(dep[top[u]]<dep[top[v]]) swap(u,v),swap(qu,qv),swa^=1;
        qu.push_back({dfn[top[u]],dfn[u]});
        u=fa[top[u]];
    }
    if(dep[u]<dep[v]) swap(u,v),swap(qu,qv),swa^=1;
    qu.push_back({dfn[v],dfn[u]});
    if(swa) swap(qu,qv);
     
    Type res;
    res.unit();
    for(int i=0;i<qu.size();i++) query(1,qu[i].first,qu[i].second,res,1/*使用線段樹上的反向信息*/);
    for(int i=qv.size()-1;i>=0;i--) query(1,qv[i].first,qv[i].second,res,0/*使用線段樹上的正向信息*/);
    return res;
}

LL query_tree(int u)
{
    return query(1,dfn[u],dfn[u]+siz[u]-1);
}

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&w[i]);
    for(int i=1;i<n;i++)
    {
        int u,v;
        scanf("%d%d",&u,&v);
        add_edge(u,v),add_edge(v,u);
    }
    
    //fa[1]=0;//注意初始化fa
    dfs1(1);
    dfs2(1,1);
    
    build(1,1,n);
    scanf("%d",&m);
    while(m--)
    {
        int t,u,v;
        LL k;
        scanf("%d",&t);
        if(t==1)
        {
            scanf("%d%d%lld",&u,&v,&k);
            modify_path(u,v,k);
        }
        else if(t==2)
        {
            scanf("%d%lld",&u,&k);
            modify_tree(u,k);
        }
        else if(t==3)
        {
            scanf("%d%d",&u,&v);
            printf("%lld\n",query_path(u,v));
        }
        else
        {
            scanf("%d",&u);
            printf("%lld\n",query_tree(u));
        }
    }
    
    return 0;
}

9.3.2.長鏈剖分

指針空間要給夠！！！

類此于重鏈剖分和樹上啟發式合并，當前節點繼承長兒子的信息，暴力合并短兒子的信息。

長鏈剖分定義的深度d2：當前節點到以此節點為根的子樹中最遠的葉子節點的距離+1。定義葉子節點的d2為1。

定義

長鏈剖分定義的深度d2：當前節點到以此節點為根的子樹中最遠的葉子節點的距離+1。定義葉子節點的d2為1。

根節點定義的深度d1：當前節點到根節點的距離。依題定義根節點的d1為0還是1。

長兒子：其子節點中子樹深度最大的子結點。如果有多個子樹最大的子結點，取其一。如果沒有子節點，就無長兒子。短兒子：剩余的子結點。

從這個結點到長兒子的邊為長邊。到其他短兒子的邊為短邊。若干條首尾銜接的長邊構成長鏈。把落單的結點也當作長鏈。

類似于重鏈剖分，整棵樹就被剖分成若干條長鏈。優先遍歷長兒子，即可保證一條長鏈是連續遍歷的。

圖片

橙色代表長兒子，紅邊代表長邊，黃色的框代表長鏈，圓圈內的數字代表遍歷順序，綠色的數字代表長鏈剖分定義的深度d2。

長鏈剖分

dfs_son：預處理所有節點的長兒子和長鏈剖分定義的深度d2 。有時根據題目還需要預處理深度d1和子樹大小son。

int d2[N],son[N];//長鏈剖分定義的深度和長兒子
//int d1[N],siz[N];//根節點定義的深度和子樹大小

void dfs_son(int u,int fa)
{
    //d1[u]=d1[fa]+1;
    //siz[u]=1;
    for(int i=h[u];i!=0;i=ne[i])
    {
        int v=e[i];
        if(v==fa) continue;
        dfs_son(v,u);
        //siz[u]+=siz[v];
        if(d2[v]>d2[son[u]]) son[u]=v;
    }
    d2[u]=d2[son[u]]+1;//此行不能放在循環里面，否則會導致葉子節點的d2為0
    return ;
}

性質

一個節點到它所在的長鏈的鏈底部的路徑，為從這個節點到它子樹每個子樹所有節點的路徑中，最長的一條。
一個深度為k 的節點向上跳一條短邊，子樹大小至少增加k+2。
- 證明圖片
一個節點到根節點的路徑，最多經過$O(\sqrt{n})$條短邊。
- 證明
  
  由性質2：一個深度為k 的節點向上跳一條短邊，子樹大小至少增加k+2。
  
  那么如果我們跳了x條短邊，此時樹的大小$>\sum_{i=1}^xi = \frac{x(x+1)}{2}$。
  
  故所有一個節點到根的路徑，最多經過$O(\sqrt{n})$條短邊。類似于重鏈剖分，這個$O(sqrt(n))$一般不滿

9.3.2.1.長鏈剖分求樹上 k 級祖先

在線算法。預處理$O(N \log N)$，詢問$O(1)$。

性質：任意一個點的k級祖先所在長鏈的鏈長一定大于等于k。

證明圖片
思路：長鏈剖分

具體思路：摘取至xht的題解

首先我們進行預處理：
1. 對樹進行長鏈剖分，記錄每個點所在鏈的頂點和深度，$O(n)$。
2. 樹上倍增求出每個點的 $2^n$ 級祖先，$O(n \log n)$。
3. 對于每條鏈，如果其長度為 len，那么在頂點處記錄頂點向上的 len 個祖先和向下的 len$ $個鏈上的兒子，$O(n)$。
4. 對 $i \in [1, n]$ 求出在二進制下的最高位 $h_i$，即$\lfloor \log_2 i \rfloor$，$O(n)$。
對于每次詢問 x 的 k 級祖先：
1. 利用倍增數組先將 x 跳到 x 的 $2^{h_k}$ 級祖先，設剩下還有 $k^{\prime}$ 級，顯然 $k^{\prime} < 2^{h_k}$，因此此時 x 所在的長鏈長度一定 $\ge 2^{h_k} > k^{\prime}$。
2. 由于長鏈長度 $>k^{\prime}$，因此可以先將 x 跳到 x 所在鏈的頂點，若之后剩下的級數為正，則利用向上的數組求出答案，否則利用向下的數組求出答案。

int n,q,root,res;
LL ans;
int h[N],e[N],ne[N],idx;    //已知父親，建單向邊

//長鏈剖分的變量
int son[N],d2[N];    //d2：長鏈剖分定義的深度
int top[N];

//k級祖先的變量
int lg2[N],fa[N][21];
vector<int> up[N],down[N];
int d1[N];//d1：根節點定義的深度

void dfs(int u,int p)
{
    top[u]=p;
    if(u==p)    //在頂點處記錄頂點向上的len個祖先和向下的len個鏈上的兒子
    {
        for(int i=1,v=u;i<=d2[u] && v!=0;i++,v=fa[v][0]) up[u].push_back(v);
        for(int i=1,v=u;i<=d2[u] && v!=0;i++,v=son[v]) down[u].push_back(v);
    }
    if(son[u]) dfs(son[u],p);
    for(int i=h[u];i!=0;i=ne[i]) if(e[i]!=son[u]) dfs(e[i],e[i]);
    return ;
}

int ask(int u,int k)
{
    if(k==0) return u;
    u=fa[u][lg2[k]],k-=1<<lg2[k];   //利用倍增數組先跳到u的2_hk級祖先
    k-=d1[u]-d1[top[u]],u=top[u]; //再跳到u所在鏈的頂點
    if(k>=0) return up[u][k];   //精準降落
    else return down[u][-k];
}

int main()
{
    scanf("%d%d",&n,&q);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&fa[i][0]);
        if(fa[i][0]!=0) add(fa[i][0],i);
        else root=i;
    }
    for(int i=2;i<=n;i++) lg2[i]=lg2[i>>1]+1;   //預處理lg2：x在二進制下的最高位hx
    dfs_son(root);
    dfs(root,root);
    for(int i=1;i<=q;i++)
    {
        scanf("%d%d",&x,&k);
        printf("%lld\n",ask(x,k));
    }
    return 0;
}

9.3.2.2.長鏈優化樹形dp$O(N)$

適用條件：把維護子樹中只與深度有關的信息做到線性的時間復雜度。因為優化的是dp，所以自然是靜態離線的。

長鏈優化樹形dp$O(N) $
維護子樹中只與深度有關的信息

樹上啟發式合并$O(N\log N)$
維護子樹中恒定不變的信息（$e.g.$節點的顏色）

設計狀態轉移方程——長鏈剖分的難點。

長鏈剖分只能優化形如$f[u][calc(i)]=f[son][i]+x,(其中i與d2相關)$的狀態轉移方程，故設計時應向這個方向設計。同時，為了下面更方便，$f[son]$****的第二維應是i，讓$f[u]$的第二維隨$f[son][i]$而定。
長鏈剖分dfs_son。
dp在維護信息的過程中，先O(1)繼承重兒子的信息，再暴力合并其余輕兒子的信息。
1. 在dp遞歸前先申請空間。
  
  指針申請空間——長鏈剖分的核心操作。
  
  定義指針：int space[N*2];int *f[N],*tmp=space;f[N][]實際上是使用space[N2]的空間，tmp“引領”f[i][]在space[N2]的地址。space空間開2倍，對于每一條長鏈申請2倍空間！這樣的話指針可以靈活地往左往右移互相不發生沖突。
  
  對于每一條新長鏈申請新空間。當即將遞歸一條新長鏈的鏈頂時，令tmp+=d2[u],f[u]=tmp,tmp+=d2[u];申請一條長鏈f[u]（由于u是該長鏈的鏈頂，故該長鏈的長度一定是d2[u]，需申請2倍空間）的空間（f[u]的地址指向原tmp），然后移動tmp為下次申請空間做準備，此時已申請空間f[u][d2[u]<<1]。
  
  當即將遞歸一個長兒子時，令f[son[u]]=f[u]+(calc(i)-i); 直接在已申請空間的長鏈上使用空間，根據狀態轉移方程令f[son[u]]地址指向f[u]+(calc(i)-i)，這樣可以自然地將長兒子的信息O(1)合并到當前節點。當即將遞歸其余的短兒子時，其一定是一條新長鏈的鏈頂，為每一條新長鏈申請空間tmp+=d2[v],f[v]=tmp,tmp+=d2[v];。
  - 圖片
    
    下圖是對于上圖那顆樹的“5回溯時”～“6回溯時”時間，操作的順序。
    
    可以發現對于每一個長鏈，其使用的空間是連續的，這樣可以自然地將長兒子的信息O(1)合并到當前節點（$e.g.$f[2][2]會O(1)繼承f[3][1]）。對于其余的短兒子，只需暴力合并即可。
2. 優先遍歷長兒子，回溯時自然地繼承長兒子的信息。
3. 遍歷短兒子，暴力合并信息。注意子結點到父節點深度+1。
上述操作對于優化$f[u][calc(i)]=\sum f[son][i]$已經足夠。但是對于1.$f[u][calc(i)]=\sum \{ f[son][i]+x \}$轉移有常量的方程；2.$f[u][i] \subset f[u][i+1]$；3.詢問的是$f[u][i]$而不是$\sum f[u]$，則可以用懶標記維護常數項保證復雜度。

懶標記正確的原因：雖然f[son][j]不能貢獻答案到f[u][i]（自然也沒有f[u][i]+=f[son][j]+x），但是$f[son][1] \subset f[son][j]$，因此對于每一個son，只需要令tag[u]加一次x即可，不會影響除f[u][0]外其他所有f[u]的正確性。

tag[u]=tag[son]+x;//懶標記（別忘了加上tag[son]），son是所有兒子
f[u][0]=-tag[u];//特判：f[u][0]沒有由任何兒子轉移而來，且不包含其他f[u]，不能加上懶標記
printf("%d\n",f[u][i]+tag[u]);

對于樹上計數類dp，考慮每次把即將要加入的子樹（新）與已加入的子樹（舊）計算貢獻（這樣可以不重不漏地計算答案）。長兒子由于是第一個加入的子樹，直接讓當前節點繼承長兒子信息，無需考慮與其他子樹計算貢獻。
對于詢問每個節點，由于長鏈剖分優化樹形dp是靜態離線的，所以先將詢問放置在各個節點vector，遞歸到當前節點并計算完成時回答。否則回溯后信息就會被父節點利用被其他子樹覆蓋。
長鏈剖分容易維護后綴和，較難維護前綴和。借助后綴和回答區間詢問。

void dp(int u,int fa)
{
    if(son[u])
    {
        f[u][0]+=f[u][1];   //在該if末尾加上該代碼
    }
    for(int i=h[u];i!=0;i=ne[i])
    {
        f[u][0]+=f[v][0];   //在該for末尾加上該代碼
    }
    return ;
}

因為每個點僅屬于一條長鏈，短兒子的d2一定小于當前節點的d2合并時長鏈一定能包含短鏈，且一條長鏈只會在鏈頂位置作為輕兒子暴力合并一次，所以時間復雜度是線性的。

int d2[N],son[N];

//長鏈剖分的核心：指針申請內存，O(1)繼承長兒子信息
int space[N*2]; //空間開2倍，對于每一條長鏈申請2倍空間！！！
int *f[N],*tmp=space;
int tp;//輔助多測清空

//對于每一條新長鏈申請空間
void dp(int u,int fa)
{
    f[u][0]=a[u];

    //優先遍歷長兒子，將長兒子的信息O(1)合并到當前節點
    if(son[u])
    {
        f[son[u]]=f[u]+1;   //對于一個長兒子，直接在已申請空間的長鏈上使用空間，根據狀態轉移方程令f[son[u]]地址指向f[u]+1，這樣可以自然地將長兒子的信息O(1)合并到當前節點
        dp(son[u],u);
        
        //ans[u]=ans[son[u]]+1;   //繼承長兒子的答案（注意深度+1）
        //tag[u]=tag[son[u]]+x;   //懶標記（別忘了加上tag[son[u]]）
    }
    
    //短兒子暴力合并
    for(int i=h[u];i!=0;i=ne[i])
    {
        int v=e[i];
        if(v==fa || v==son[u]) continue;
        
        tmp+=d2[v],f[v]=tmp,tmp+=d2[v];  //對于其余的短兒子，其一定是一條新長鏈的鏈頂，為每一條新長鏈申請空間
        tp+=d2[v]*2;
        dp(v,u);
        
        for(int j=0;j<d2[v];j++)    //注意是[0,d2[v])
        {
            f[u][j+1]+=f[v][j]; //注意深度+1
        }
        //tag[u]+=tag[v]+x;
    }
    
    //f[u][0]=-tag[u];//特判：f[u][0]沒有由任何兒子轉移而來，不能加上懶標記
    //printf("%d\n",f[u][i]+tag[u]);
    return ;
}

//多測清空
for(int u=1;u<=n;u++) son[u]=0;
for(int i=0;i<=tp+1/*多清空一些總沒問題*/;i++) space[i]=0;
tp=0;
tmp=space;

dfs_son(1,-1);

tmp+=d2[1],f[1]=tmp,tmp+=d2[1];  //申請一條長鏈f[1]（由于1是該長鏈的鏈頂，故該長鏈的長度一定是d2[1]，需申請2倍空間）的空間（f[1]的地址指向原tmp），然后移動tmp為下次申請空間做準備，此時已申請空間f[1][d2[1]<<1]
tp+=d2[1]*2;
dp(1,-1);

vector實現指針

思路仍然是用 vector 存下每個點的信息。不過有幾個特殊之處：
1. 按深度遞增的順序存儲的話，因為合并重兒子信息時要在開頭插入元素，效率低下。所以考慮按深度遞減的順序存儲信息。
2. 合并重兒子信息的時候，直接用 swap 交換而不是復制，在時間和空間上都更優（swap 交換 vector 的時間復雜度是 $O(1)$ 的）。

#include<bits/stdc++.h>
using namespace std;

const int N=1e6+10,M=N*2;
int n;
int ans[N];

int h[N],e[M],ne[M],idx;

int son[N],d2[N];
vector<int> f[N];

void dp(int u,int fa)
{
    if(son[u])
    {
        dp(son[u],u);
        
        swap(f[u],f[son[u]]);
        f[u].push_back(1);
        
        ans[u]=ans[son[u]];
        if(f[u][ans[u]]==1) ans[u]=d2[u];
        
        for(int i=h[u];i!=0;i=ne[i])
        {
            int v=e[i];
            if(v==fa || v==son[u]) continue;
            dp(v,u);
            for(int i=d2[v]-1;i>=0;i--)
            {
                int tmp=i+d2[u]-d2[v]-1;
                f[u][tmp]+=f[v][i];
                if(f[u][tmp]>f[u][ans[u]] || (f[u][tmp]==f[u][ans[u]] && tmp>ans[u])) ans[u]=tmp;
            }
        }
    }
    else
    {
        f[u].push_back(1);
        ans[u]=0;
    }
    return ;
}

int main()
{
    scanf("%d",&n);
    for(int i=1;i<n;i++)
    {
        int u,v;
        scanf("%d%d",&u,&v);
        add(u,v),add(v,u);
    }
    dfs_son(1,-1);
    dp(1,-1);
    for(int i=1;i<=n;i++) printf("%d\n",d2[i]-ans[i]);
    return 0;
}

9.4.虛樹$O(cnt_{key}\log cnt_{key}+ F(cnt_{key}))$

適用條件：q組詢問，每組詢問給定若干個關鍵點。答案只與關鍵點及其到根節點之間的鏈有關，其他節點和邊的信息可以且能迅速合并到那些鏈。“$cnt_{key} ≤$”。

建立虛樹的時間復雜度：$O(cnt_{key}\log cnt_{key})$。虛樹的大小：$O(cnt_{key})$。

$O(q*F(N))→O(cnt_{key}\log cnt_{key}+ F(cnt_{key}))$。

思考對于一次詢問正常的樹怎么$O(F(N))$解決。
dfs預處理dfs序、LCA。步驟4的合并信息有時可以在這里直接$O(N)$預處理。
對于每一組詢問，標記關鍵點并建立虛樹。建立虛樹的時間復雜度是$O(cnt_{key}\log cnt_{key})$。注意從此開始要保證復雜度與關鍵點（而不是N）相關，尤其注意初始化的復雜度要與關鍵點（而不是N）相關。

虛樹=關鍵點+任意兩個關鍵點的LCA。

前置知識：《圖論8.4.拓展應用1.點集LCA》。
思考對于虛樹上的一條邊，怎么將其對應的原樹上的鏈上的所有點及其其他子樹的信息合并。
根據步驟1，在虛樹上解決問題。

int n,m,q;
int h[N],e[M],ne[M],idx;    //原樹
int dfn[N],num; //dfs序
int fa[N][19],dep[N];
vector<int> key;
bool is_key[N];
//int st[N],top;  //用單調棧來維護一條虛樹上的鏈
int hc[N],ec[M],nc[M],cidx; //虛樹

bool cmp(int x,int y)
{
    return dfn[x]<dfn[y];
}

//建立虛樹方法一：二次排序+LCA連邊
int build()
{
    sort(key.begin(),key.end(),cmp);
    int backup=key.size();
    for(int i=1;i<backup;i++) key.push_back(lca(key[i-1],key[i]));
    sort(key.begin(),key.end(),cmp);
    key.erase(unique(key.begin(),key.end()),key.end());
    for(auto u : key) hc[u]=0;//在build()函數中要清空虛樹的鄰接表
    for(int i=1;i<key.size();i++) cadd(lca(key[i-1],key[i]),key[i]);
    return key[0];
}

/*建立虛樹方法二：單調棧
//用單調棧來維護一條虛樹上的鏈
//在build()函數中要清空虛樹的鄰接表
int build()
{
    top=0;

    //將關鍵點按照dfs序排序
    sort(key.begin(),key.end(),cmp);
    
    //先將1號節點入棧，清空1號節點的鄰接表
    hc[1]=0;
    st[++top]=1;
    
    for(auto u : key)
    {
        if(u==1) continue;  //不要重復添加1號節點
        
        //先添加LCA。要保證虛樹中任意2個節點的LCA也在虛樹中
        int p=lca(u,st[top]);
        if(p!=st[top])  //如果LCA和棧頂元素不同，則說明當前節點不再當前棧所存的鏈上
        {
            while(dfn[st[top-1]]>dfn[p])    //當次大節點的dfs序大于lca的dfs序時
            {
                cadd(st[top-1],st[top]);
                top--;
            }
            if(st[top-1]==p)    //如果此時次大節點是LCA
            {
                cadd(st[top-1],st[top]);
                top--;
            }
            else    //否則說明LCA從來沒有入過棧
            {
                hc[p]=0;    //清空即將入棧的LCA的鄰接表
                cadd(p,st[top]);    //注意此時st[top]的連邊
                top--;
                st[++top]=p;
            }
        }
        
        //再添加點u
        hc[u]=0;    //清空即將入棧的點u的鄰接表
        st[++top]=u;
    }
    
    //對剩余的最后一條的鏈進行連邊
    while(top-1)
    {
        cadd(st[top-1],st[top]);
        top--;
    }
    
    return 1;
}
*/

scanf("%d",&n);
for(int i=1;i<n;i++)
{
    int u,v;
    scanf("%d%d",&u,&v);
    add(u,v),add(v,u);
}
dep[1]=1;
dfs(1); //dfs預處理dfs序、LCA。步驟4的合并信息有時可以在這里直接O(N)預處理
scanf("%d",&q);
while(q--)
{
    //注意初始化的復雜度要與關鍵點（而不是N）相關
    //在build()函數中再清空虛樹的鄰接表
    cidx=0;
    for(auto u : key)
    {
        is_key[u]=false;
        ans[u]=0;
    }
    key.clear();
    
    scanf("%d",&m);
    for(int i=1;i<=m;i++)
    {
        int k;
        scanf("%d",&k);
        key.push_back(k);
        is_key[k]=true;
    }
    int vr=build();//返回虛樹的根節點
    //根據步驟1，接下來在虛樹上解決問題
}

9.5.Link-Cut-Tree

動態樹問題：
維護一個森林，支持刪除某條邊，加入某條邊，并保證加邊，刪邊后仍是!!森林!!。我們要維護該森林的一些信息。
一般的操作有兩點連通性， 兩點路徑權值和， 連接兩點 和 切斷某條邊、修改信息 等

LCT 則是用多個** Splay** 來維護 多個實鏈，Splay 的特性就使得我們可以進行 樹的合并、分割操作。LCT 基本能代替樹鏈剖分，LCT處理一次詢問的時間復雜度為$ O(log?n)$，但是常數大。

實邊和虛邊可以任意選擇，一個點與他的兒子最多只有1條實邊。只要有邊，兒子都會儲存父親的信息，但父親只會儲存實邊的兒子的信息。

輔助樹splay

輔助樹由多棵 Splay 組成，每棵 Splay 維護原樹中的一條路徑，且中序遍歷這棵 Splay 得到的點序列，從前到后對應原樹“從上到下”的一條路徑。原樹每個節點與輔助樹的 Splay 節點一一對應。
對于每一條實邊路徑，我們用一個splay維護，splay的中序遍歷（而不是左右兒子）就是原樹的路徑。
對于每一條虛邊路徑，各棵 Splay 之間并不是獨立的：每棵 Splay 的根節點的父親節點本應是空，但在 LCT 中每棵 Splay 的根節點的父親節點指向原樹中這條鏈的父親節點（即鏈最頂端的點的父親節點）。這類父親鏈接與通常 Splay 的父親鏈接區別在于兒子認父親，而父親不認兒子，對應原樹的一條虛邊。因此，每個連通塊恰好有一個點的父親節點為空。

輔助樹和原樹的關系

原樹中的實鏈在輔助樹中都在同一顆 Splay 里。
原樹中的虛鏈 : 在輔助樹中，子節點所在 Splay 的 Father 指向父節點，但是父節點的兩個兒子都不指向子節點。
原樹的 Father 指向不等于輔助樹的 Father 指向。
輔助樹是可以在滿足輔助樹、Splay 的性質下任意換根的。
虛實鏈變換可以輕松在輔助樹上完成，這也就是實現了動態維護樹鏈剖分。

make_root()不會影響整顆樹的拓撲結構。

一個小技巧：把帶權的邊拆成點，這樣LCT也能解決帶邊權的問題。

#u      #u (0)
|       |
|w  ->  #i+n (w)
|       |
#v      #v (0)

#define ls tr[u].kid[0]
#define rs tr[u].kid[1]
int n,m;
struct Tree
{
    int kid[2],p;
    int key,sum;
    int rev;
}tr[N];

void eval(int u)
{
    swap(ls,rs);
    tr[u].rev^=1;
    return ;
}

void pushup(int u)
{
    tr[u].sum=tr[ls].sum^tr[u].key^tr[rs].sum;
    return ;
}

void pushdown(int u)
{
    if(tr[u].rev==1)
    {
        eval(ls);
        eval(rs);
        tr[u].rev=0;
    }
    return ;
}

bool is_root(int u)
{
    return tr[tr[u].p].kid[0]!=u && tr[tr[u].p].kid[1]!=u;
}

int dir(int u)
{
    return tr[tr[u].p].kid[1]==u;
}

void rotate(int u)
{
    int y=tr[u].p,z=tr[y].p;
    int tu=dir(u),ty=dir(y);
    if(!is_root(y)) tr[z].kid[ty]=u;    //注意這里的特判，否則會多連一條實邊
    tr[u].p=z;
    tr[y].kid[tu]=tr[u].kid[tu^1],tr[tr[u].kid[tu^1]].p=y;
    tr[u].kid[tu^1]=y,tr[y].p=u;
    pushup(y);  //別忘了這里
    pushup(u);
    return ;
}

void splay(int u)
{
    //先自上而下pushdown
    int top=0,st[N];
    for(int i=u;;i=tr[i].p)
    {
        st[++top]=i;
        if(is_root(i)) break;
    }
    while(top) pushdown(st[top--]);
    
    while(!is_root(u))
    {
        int y=tr[u].p;
        if(!is_root(y))
            if(dir(u)^dir(y)) rotate(u);
            else rotate(y);
        rotate(u);
    }
    
    return ;
}

void access(int u)  //建立一條從原根到u的實邊路徑，同時將u變成splay的根節點，并且將u與u的子節點的邊變為虛邊
{
    int backup=u;
    for(int i=0;u!=0;i=u,u=tr[u].p) //i從0開始：將u與u的子節點的邊變為虛邊
    {
        splay(u);
        tr[u].kid[1]=i;
        pushup(u);  //別忘了這里
    }
    splay(backup);
    return ;
}

void make_root(int u)   //將u變成原樹的根節點，同時access函數將u變成splay的根節點
{
    access(u);
    eval(u);
    return ;
}

int find_root(int u)    //找到u所在原樹的根節點, 再將原樹的根節點旋轉到splay的根節點，并將u到根節點的路徑變為實邊
{
    access(u);
    //access后u是splay的根節點，找原樹的根一直往左兒子找即可
    while(tr[u].kid[0]!=0)
    {
        pushdown(u);    //別忘了這里
        u=tr[u].kid[0];
    }
    splay(u);
    return u;
}

void split(int u,int v) //給u和v之間的路徑建立一個splay，原樹的根是u，splay的根是v
{
    make_root(u);
    access(v);
    return ;
}

void link(int u,int v)  //如果u和v不連通，則加入一條u和v的虛邊，v是u的父節點
{
    make_root(u);
    if(find_root(v)!=u) tr[u].p=v;
    return ;
}

void cut(int u,int v)   //如果u和v之間存在邊，則刪除該邊
{
    make_root(u);
    if(find_root(v)==u/*要把u到v變為實邊路徑*/ && tr[v].p==u && tr[v].kid[0]==0)    //???
    {
        tr[u].kid[1]=tr[v].p=0;
        pushup(u);  //別忘了這里
    }
    return ;
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",&tr[i].key);
    while(m--)
    {
        int op,x,y,w;
        scanf("%d",&op);
        if(op==0)
        {
            scanf("%d%d",&x,&y);
            split(x,y);
            printf("%d\n",tr[y].sum);
        }
        else if(op==1)
        {
            scanf("%d%d",&x,&y);
            link(x,y);
        }
        else if(op==2)
        {
            scanf("%d%d",&x,&y);
            cut(x,y);
        }
        else
        {
            scanf("%d%d",&x,&w);
            splay(x);
            tr[x].key=w;
            pushup(x);
        }
    }
    return 0;
}

9.6.樹形dp

《動態規劃3.樹形dp》

動態規劃

9.7.樹上啟發式合并

《基礎算法12.2.樹上啟發式合并》

10.DLX

10.1.十字鏈表

數據結構

int idx;
int u[N],d[N],l[N],r[N];//十字鏈表。編號為i的點的上、下、左、右的點的編號
int row[N],col[N];//編號為i的點的行和列
int s[N];//第i列有多少個1

精確覆蓋與重復覆蓋的共同函數

初始化表頭init()
逐行插入1add(雙指針hh、tt，插入1的所在的行、列)
主函數
1. 十字鏈表初始化表頭。
2. 根據題目條件逐行插入“1”。

//十字鏈表初始化表頭
void init()
{
    for(int i=0;i<=m;i++)
    {
        l[i]=i-1,r[i]=i+1;
        u[i]=d[i]=i;
        s[i]=0;//多組測試數據
    }
    l[0]=m,r[m]=0;
    idx=m+1;
    return ;
}

//插入十字鏈表
void add(int &hh,int &tt,int x,int y)
{
    row[idx]=x,col[idx]=y,s[y]++;
    u[idx]=y,d[idx]=d[y],u[d[y]]=idx,d[y]=idx;
    r[hh]=idx,l[tt]=idx,r[idx]=tt,l[idx]=hh;
    tt=idx; //不要忘記這里
    idx++;
    return ;
}

scanf("%d%d",&n,&m);
init();
for(int i=1;i<=n;i++)//逐行插入1
{
    int hh=idx,tt=idx;
    for(int j=1;j<=m;j++)
    {
        int x;
        scanf("%d",&x);
        if(x==1) add(hh,tt,i,j);
    }
}

刪除`remove()`+恢復`resume()`的圖解

圖解

注意恢復和刪除要對稱。

注意從l/r/u/d[p]循環刪除時要先刪除p（因為終止條件是i!=p）。

刪除只是把指針指向別的地方，并沒有刪除這個節點本身，因此可以恢復。

10.2.精確覆蓋問題

瓶頸：必須是稀疏矩陣。

ans的儲存使用棧。int ans[N],aidx;

刪除（或恢復）`removee(刪除的列的哨兵（也就是第p列中的p）)`

下面以刪除為例：

傳入的是哨兵removee(刪除的列的哨兵（也就是第p列中的p）)。

刪除p所在的列（此列已被覆蓋，無需再考慮）：直接在表頭刪除。
刪除p這一列所有含1的行（此行已經選過了，或者它不能再選了（再選會導致某一列被覆蓋多次））：在鏈表里刪除。

//刪除p所在的列及p這一列所有含1的行，排除不可能答案剪枝
//從l/r/u/d[p]循環刪除時要先刪除p（因為終止條件是i!=p）
//刪除只是把指針指向別的地方，并沒有刪除這個節點本身，因此可以恢復
void removee(int p)//傳入的是列的表頭（也就是第p列中的p ）
{
    //刪除p所在的列直接在表頭刪除
    r[l[p]]=r[p],l[r[p]]=l[p];
    
    //刪除p所在的行在鏈表里刪除
    for(int i=d[p];i!=p;i=d[i]/*這里及下文極容易誤寫成i=d[p]，要小心！！！*/)
        for(int j=r[i];j!=i;j=r[j])
        {
            s[col[j]]--;
            u[d[j]]=u[j],d[u[j]]=d[j];
        }
        
    return ;
}

//恢復和刪除要對稱
void resume(int p)
{
    for(int i=u[p];i!=p;i=u[i])
        for(int j=l[i];j!=i;j=l[j])
        {
            u[d[j]]=j,d[u[j]]=j;
            s[col[j]]++;
        }
    r[l[p]]=p,l[r[p]]=p;
    return ;
}

深搜`dfs()`

爆搜，直至存儲1的十字鏈表已經沒有1了，成功返回。

選擇1的個數最少的列，記為p。優先搜索分枝少的節點的剪枝。
先刪除p這一列（此列已被覆蓋，無需再考慮）。排除不可能答案剪枝。
枚舉選出行q。將選擇的行q記入答案，刪除行q上所有含1的列（此列已被覆蓋，無需再考慮），繼續向下遞歸。回溯時恢復。若沒有可以選擇的行則失敗返回。

刪除列removee(刪除的列)時，會把p這一列所有含1的行刪除（此行已經選過了，或者它不能再選了（再選會導致某一列被覆蓋多次））。

bool dfs()
{
    if(r[0]==0) return true;    //存儲1的十字鏈表已經沒有1了
    
    //選擇1的個數最少的列，記為p
    int p=r[0];
    for(int i=r[0];i!=0;i=r[i]) if(s[i]<s[p]) p=i;
    
    //先刪除p
    removee(p);
    
    //枚舉選出行q
    for(int i=d[p];i!=p;i=d[i])
    {
        ans[++aidx]=row[i];
        for(int j=r[i];j!=i;j=r[j]) removee(col[j]);
        if(dfs()) return true;
        for(int j=l[i];j!=i;j=l[j]) resume(col[j]);
        aidx--;
    }
    resume(p);
    return false;
}

if(dfs())
{
    for(int i=1;i<=aidx;i++) printf("%d ",ans[i]);
    puts("");
}
else puts("No Solution!");

建模應用

“恰好”，“不重不漏”。

原問題的方案$\Leftrightarrow$精確覆蓋問題的方案

行表示決策，列表示“恰好”限制。

一般來說有三條核心思路建模：

行表示決策，每行（決策）對應著一個這一行所有含1的列的集合（“恰好”限制），也就對應著選 / 不選；
列表示限制，因為第 $i$ 列對應著某個條件 $P_i$。限制條件應抓住“1”這個關鍵字眼，它正好對應著精確覆蓋問題中每一列恰好被某一行覆蓋一次。
“1”：選擇這一行代表選擇這一個決策，會對這一行所有含1的列都產生影響。每一列只能被覆蓋“1”次。

10.3.重復覆蓋問題

由于重復覆蓋較精確覆蓋缺少了許多排除不可能答案剪枝，因此使用IDA*優化。

瓶頸：答案（選擇的行數）不能太大，因為IDA*遞歸的層數不能太多。

ans的儲存靠IDA*中的當前深度。

初始化表頭`init()`

需要額外記錄哨兵所在的列，刪除和恢復的時候要用。col[i]=i;

估價函數`h()`

遍歷當前所有還沒有被覆蓋的列。
對于每一列，把能覆蓋這一列的所有行全部選上，但是只當作選擇了 1 行。

這樣一來，不僅比最優解多選了一些行，還計算了比最優解更小不超過最優解的代價，滿足估價函數≤最優解。

bool vis[M];//vis[col]：第col列有沒有被覆蓋

int h()
{
    int res=0;
    memset(vis,0,sizeof vis);
    for(int i=r[0];i!=0;i=r[i])
    {
        if(vis[col[i]]) continue;
        vis[col[i]]=true;
        res++;
        for(int j=d[i];j!=i;j=d[j])
            for(int k=r[j];k!=j;k=r[k])
                vis[col[k]]=true;
    }
    return res;
}

刪除（或恢復）`removee(點的編號)`

下面以刪除為例：

傳入的是點的編號removee(點的編號)。

只需刪除這一列：把這一列所有點的左右關系改變就行（之后無論是從表頭枚舉還是遍歷一行中含1的列都不會再考慮這一列了，此列已被覆蓋，無需再考慮），不涉及行的刪除（因為可以重復覆蓋）。

注意這里不可以改變傳入的點的編號的左右關系，因為在IDA*中是遍歷一行中含1的列，一個一個刪除左右關系。倘若改變了p的左右關系，就沒有辦法遍歷這一行了。而且少改變這一左右關系不會影響答案。

void removee(int p)//這里傳入的是十字鏈表中任意一點的編號
{
    //重復覆蓋問題：對于一列中的所有點都要改變左右關系，且不涉及行的刪除
    //注意這里不可以改變p的左右關系，因為在IDA*中是遍歷一行中含1的列，一個一個刪除左右關系。倘若改變了p的左右關系，就沒有辦法遍歷這一行了。而且少改變這一左右關系不會影響答案
    for(int i=d[p];i!=p;i=d[i])
    {
        r[l[i]]=r[i];
        l[r[i]]=l[i];
    }
    return ;
}

void resume(int p)//恢復和刪除要對稱
{
    for(int i=u[p];i!=p;i=u[i])
    {
        r[l[i]]=i;
        l[r[i]]=i;
    }
    return ;
}

迭代加深`IDA_star()`

迭代加深，直至存儲1的十字鏈表已經沒有1了，成功返回。

若估價函數h()+當前深度k>規定深度，失敗返回。
選擇1的個數最少的列，記為p。優先搜索分枝少的節點的剪枝。
枚舉選出行q。將選擇的行q記入答案，刪除列p和行q上所有含1的列（此列已被覆蓋，無需再考慮），繼續向下遞歸。回溯時恢復。若沒有可以選擇的行則失敗返回。

刪除列removee(點的編號)時，傳入的是點的編號，只把這一列所有點的左右關系改變就行（之后無論是從表頭枚舉還是遍歷一行中含1的列都不會再考慮這一列了，此列已被覆蓋，無需再考慮），不涉及行的刪除（因為可以重復覆蓋）。

bool IDA_star(int k,int depth)
{
    if(k+h()>depth) return false;
    if(r[0]==0) return true;
    int p=r[0];
    for(int i=r[0];i!=0;i=r[i]) if(s[i]<s[p]) p=i;
    for(int i=d[p];i!=p;i=d[i])
    {
        ans[k]=row[i];
        removee(i);
        for(int j=r[i];j!=i;j=r[j]) removee(j);
        
        if(IDA_star(k+1,depth)) return true;
        for(int j=l[i];j!=i;j=l[j]) resume(j);
        resume(i);
    }
    return false;
}

//注意這里的depth
int depth=0;
while(!IDA_star(0,depth)) depth++;
printf("%d\n",depth);
for(int i=0;i<depth;i++) printf("%d ",ans[i]);  //注意這里不取等號

建模應用

“至少選出多少個……才能滿足”。

原問題的方案$\Leftrightarrow$精確覆蓋問題的方案

行表示決策，列表示“至少……滿足”限制。

行表示決策，每行（決策）對應著一個這一行所有含1的列的集合（“至少……滿足”限制），也就對應著選 / 不選；
列表示限制，因為第 $i$ 列對應著某個條件 $P_i$。
“覆蓋”：限制條件不用再抓住“1”的要素，只需要抓住“覆蓋”要素。

posted @ 2025-10-14 00:52 Brilliance_Z 閱讀(25) 評論(0) 收藏舉報

刷新頁面返回頂部

BrillianceZ

數據結構·字符串和圖

1.字符串的存儲

1.1.字符數組和STLstring

char s[N]

string s

1.2.\(Trie\)樹

1.2.1.\(Trie\)樹

1.2.2.\(01Trie\)樹

1.2.2.1.求\(a\operatorname{xor}b_i\)的最值

方法一：\(01Trie\)樹\(O(N\log N)\)

方法二：\(01Trie\)思想+值域線段樹\(O(N\log^2 N)\)

2.字符串的表示

2.1.字符串\(Hash\)

2.2.字符串的最小表示法

3.字符串組前綴問題

4.字符串組匹配問題和字符串子串周期問題

4.1.一匹一：KMP算法

4.1.1.KMP\(O(N)\)

字符串子串周期問題

4.1.2.擴展KMP（Z函數）\(O(N)\)

應用

4.2.一匹多：AC自動機

功能

應用

5.字符串子串問題

5.1.后綴數組

5.2.后綴自動機

功能

復雜度

C++代碼

6.字符串回文子串問題

6.1.manacher算法 \(O(n)\)

6.2.hash \(O(nlogn)\)

6.3.dp\(O(N^2)\)

7.鄰接表

8.并查集（無向圖的連通性、動態維護傳遞性關系）

8.1.并查集的優化方式

8.1.1.路徑壓縮并查集

8.1.2.按秩合并并查集

8.2.并查集的拓展方式

8.2.1.“擴展域”并查集（思路更簡潔，但是空間更大）

8.2.2.“邊帶權”并查集

9.樹上問題

9.1.樹上莫隊

9.2. 樹上分治算法

9.2.1.點分治

常用技巧

9.2.2.動態點分治（點分樹）

預處理

詢問

9.3.樹鏈剖分

9.3.1.重鏈剖分

名詞

預處理

路徑→\(O(\log n)\)條重鏈（區間）

子樹→1個區間

鄰域

代碼

9.3.2.長鏈剖分

圖片

長鏈剖分

性質

9.3.2.1.長鏈剖分求樹上 k 級祖先

9.3.2.2.長鏈優化樹形dp\(O(N)\)

9.4.虛樹\(O(cnt_{key}\log cnt_{key}+ F(cnt_{key}))\)

9.5.Link-Cut-Tree

9.6.樹形dp

9.7.樹上啟發式合并

10.DLX

10.1.十字鏈表

數據結構

精確覆蓋與重復覆蓋的共同函數

刪除remove()+恢復resume()的圖解

10.2.精確覆蓋問題

刪除（或恢復）removee(刪除的列的哨兵（也就是第p列中的p）)

深搜dfs()

建模應用

10.3.重復覆蓋問題

初始化表頭init()

1.1.字符數組和STL`string`

`char s[N]`

`string s`

刪除`remove()`+恢復`resume()`的圖解

刪除（或恢復）`removee(刪除的列的哨兵（也就是第p列中的p）)`

深搜`dfs()`

初始化表頭`init()`

估價函數`h()`

刪除（或恢復）`removee(點的編號)`

迭代加深`IDA_star()`