圖論指標在認知神經科學或腦科學的研究中，通常作為研究腦網絡表現的描述性指標之一，而圖論指標從全局性來分可以分為：節點指標和全局指標，而根據描述腦網絡整合性表現又可分為：整合指標和分離指標。

該隨筆主要涉及圖論指標中全局指標及整合指標的全局集群系數，英文全稱為Global Clustering coefficient。

在學習該指標前，我們需要先了解一個核心概念——三角形。聽起來，這個概念似乎很簡單。是的！這個概念并不復雜，甚至可以說非常簡單。現在，我們可以在紙上畫出一個三角形，這個三角形有邊，而邊與邊相交處便是交點。在認知神經科學研究中，無論是fMRI、fNIRS或者是EEG，我們在收集腦信號都是基于點的，如fMRI的體素，fNIRS和EEG的通道。這些點邊可以看成是三角形的交點，而但點與點之間存在相關時便可以連成邊，而三個這樣的邊便可以形成三角形。

在整個腦網絡中，能夠形成三角形數量的多少決定了整個網絡傾向于形成緊密連接群體的程度，也即整合程度。

那么問題就來了，為什么我們會選擇三角形作為最基本的元素？
“三人成虎”，一個中國成語可能能很好地解釋這個問題。相比于兩個節點形成的邊，三個節點形成的三角能夠提供更為豐富的信息，它體現了群體效應。三角形形成了完整的閉環關系，這種結構表征了節點間更為復雜的交互模式，它是一種社區結構。最后，在實際中，三角形在信息傳遞和冗余性上有著一定的優勢，例如三角形中即使某一個邊出現問題，信息仍然可以有效傳遞。

回歸正題！那么全局集群系數是怎么計算的？

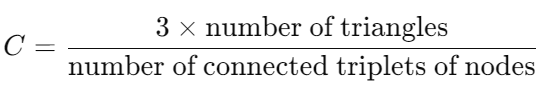
全局聚類系數通常定義為網絡中實際存在的三角形數量與能夠形成三角形的三元組（由三個節點構成，其中至少有兩條邊將它們連接起來）數量的比值。

相應的，既然具有全局集群系數，那就存在局部集群系數，該指標的意義請關注后續更新內容。