邏輯斯蒂回歸
B站視頻鏈接 5 邏輯斯蒂回歸
0 模型引入
該模型主要是一個(gè)分類問(wèn)題,這一次主要用的就是邏輯斯蒂回歸.
在上一屆課程中我們使用了線性回歸,咱們使用的模型是普通的一階線性模型\(\hat{y}=x*\omega+b\),并且使用求和損失的方式計(jì)算損失函數(shù)\(loss=(\hat{y}-y)^{2}=(x\cdot\omega-y)^{2}\)。

但是在很多的學(xué)習(xí)過(guò)程中,我們要做的是分類的處理操作。譬如下面這個(gè)例子,將模型分成各個(gè)數(shù)據(jù)的分類集合,我們需要估算任何一個(gè)圖像屬于哪一種數(shù)據(jù)。

這個(gè)是很難使用線性模型進(jìn)行輸出的,因?yàn)檫@個(gè)玩意兒并非是具體數(shù)據(jù)上的比較,而是抽象的特征上面的類別比較。
我們這里輸出的應(yīng)當(dāng)是個(gè)概率,在這個(gè)例子中,我們輸出的就是該圖像屬于每一個(gè)分類的一個(gè)概率值,最后我們要找到概率最大的一項(xiàng)。
1 數(shù)據(jù)集的使用
這里咱們用的就是\(torch\)中自帶的一些數(shù)據(jù)集可以直接進(jìn)行使用。
1 MNIST dataset
import torchvision
train_set = torchvision.datasets.MNIST(root='../../dataset/mnist', train=True, download=True)
test_set = torchvision.datasets.MNIST(root='../../dataset/mnist', train=False, download=True)
2 CIFAR dataset
import torchvision
train_set = torchvision.datasets.CIFAR10(...)
test_set = torchvision.datasets.CIFAR10(...)
2 初步介紹
2.1 二分模型
之前咱們?cè)谂e例使用線性模型的時(shí)候舉了一個(gè)比較簡(jiǎn)單的例子:
假設(shè)咱們的輸入?yún)?shù)是學(xué)習(xí)的時(shí)間,輸出參數(shù)是該門科目最后期末考試的分?jǐn)?shù)。
現(xiàn)在咱們將這個(gè)分?jǐn)?shù)進(jìn)行一次重新定義,我們將分?jǐn)?shù)大于6的定義成通過(guò)\(pass\),分?jǐn)?shù)小于6的定義成未通過(guò)\(fail\)。
這個(gè)時(shí)候咱們的模型就成了,輸入的是學(xué)習(xí)時(shí)間,輸出的是兩個(gè)類型(要么是1要么是0)。
像是這樣子的只有兩個(gè)類型的分類問(wèn)題就是所謂的二分問(wèn)題。最后我們需要計(jì)算的是這兩個(gè)類別的概率分布。
但是由于他的輸出只有兩個(gè)參數(shù)因此,滿足下面的公式.
因此對(duì)于二分問(wèn)題咱們只需要求解其中一個(gè)類型的概率即可,也就是計(jì)算\(P(\hat{y}=1)\)的概率。
2.2 邏輯斯蒂函數(shù)
之前咱們的線性模型輸出的是一個(gè)實(shí)數(shù)\(R\),但是現(xiàn)在這個(gè)的是一個(gè)概率,因此我們需要將實(shí)數(shù)上的數(shù)用一個(gè)函數(shù)映射到\([0,1]\)之前中,這個(gè)函數(shù)就是在概率論里面經(jīng)常用到的函數(shù):
現(xiàn)在我們看一下這個(gè)函數(shù)的兩個(gè)極限:
- 當(dāng)\(x\)區(qū)域正無(wú)窮時(shí),函數(shù)的極限為\(1\)。
- 當(dāng)\(x\)趨于負(fù)無(wú)窮時(shí),函數(shù)的極限為\(0\)。
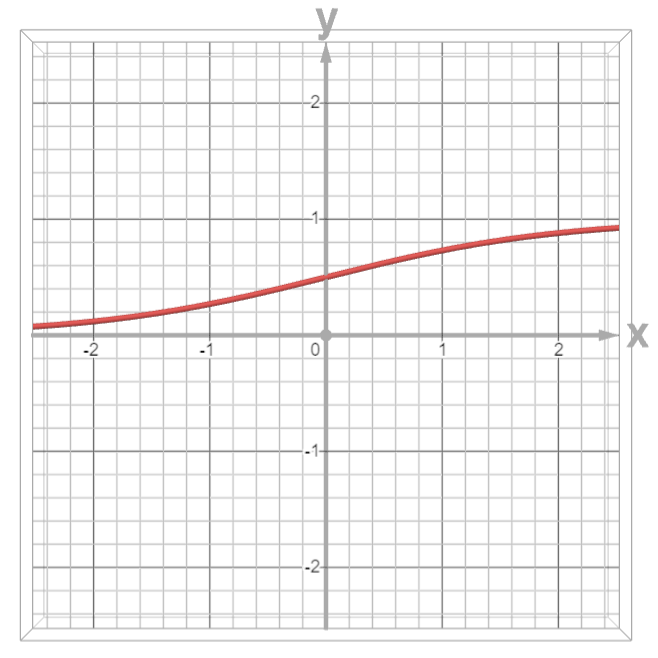
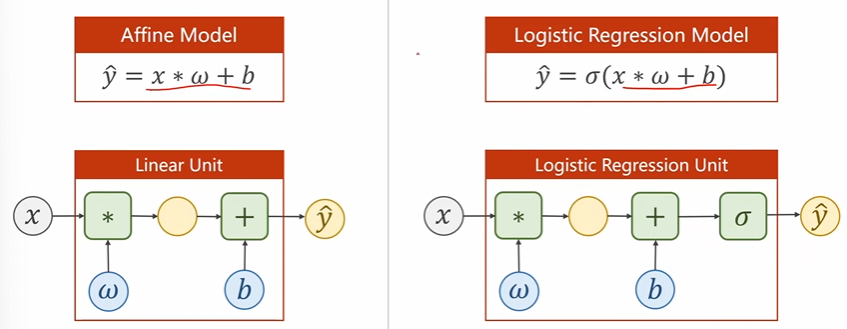
這個(gè)時(shí)候咱們就可以進(jìn)行分類了。咱們現(xiàn)在可以使用線性模型配合這個(gè)函數(shù)進(jìn)行相對(duì)應(yīng)的變換了。將函數(shù)從原本的線性模型變換成這個(gè)邏輯斯蒂模型。,僅僅只是多計(jì)算一個(gè)函數(shù)罷了。
原本的線性模型函數(shù)為:\(\hat{y}={x*\omega+b}\)
現(xiàn)在的邏輯斯蒂模型函數(shù)為:\(\hat{y}=\sigma(x*\omega+b)\)
又因?yàn)檫壿嬎沟俚暮瘮?shù)為:\(f(x) = \frac{1}{1+e^{-x}}\)
因此將其全部帶入可以得到他的基本模型為:
那么他的損失函數(shù)也要相應(yīng)的進(jìn)行變化:
原本的是:
現(xiàn)在的是:
注意:我們這里求解的是分布之間的差異,這里用的就是交叉熵\(corss - entropy\)。
舉個(gè)例子吧:
現(xiàn)在有一個(gè)分布\(P_{D}\):\(\begin{gathered}P_{D}(x=1)=0.2\\P_{D}(x=2)=0.3\\P_{D}(x=3)=0.5\end{gathered}\);另一個(gè)分布\(P_{T}\):\(\begin{gathered}P_{T}(x=1)=0.3\\P_{T}(x=2)=0.4\\P_{T}(x=3)=0.3\end{gathered}\)。
那么就可以用:\(\sum_{i}P_{0}(x-i)\ln P_{T}(x=i)\)來(lái)表示兩個(gè)分布之間的差異大小,我們希望這個(gè)數(shù)據(jù)越大越好,這也就是交叉熵。
而上面用的是二分形的交叉熵:\(loss=-(y\log\hat{y}+(1-y)\log(1-\hat{y}))\)
而這個(gè)損失就是BCE損失函數(shù)。
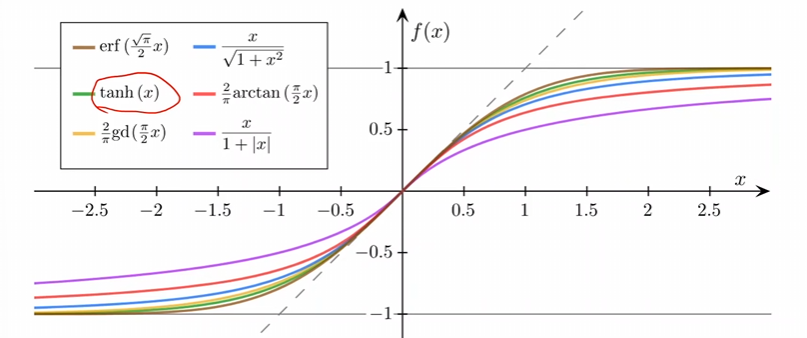
但是實(shí)際上由很多的變換飽和函數(shù)。
這個(gè)函數(shù)由幾個(gè)性質(zhì):
- 是飽和函數(shù);
- 左極限為0,右極限為1;
- 函數(shù)是嚴(yán)格單調(diào)遞增的。
如果有多個(gè)樣本直接求均值即可。
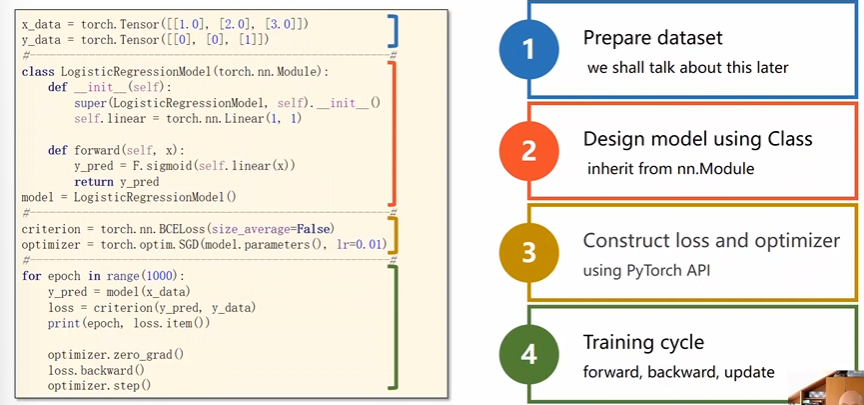
3 代碼說(shuō)明
3.1 分塊說(shuō)明
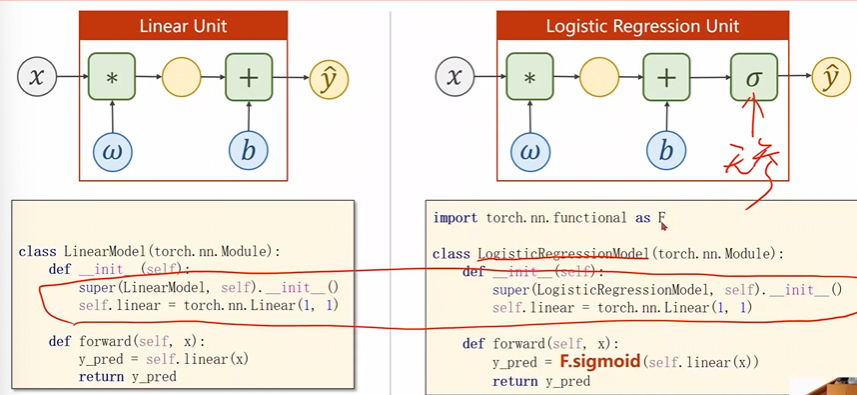
多了一步邏輯斯蒂函數(shù)的變化

原本咱們使用的是\(MSE\)損失現(xiàn)在用的是\(BCE\)損失,這個(gè)\(size_average\)是規(guī)定是否需要求各個(gè)批量的均值,影響的就是學(xué)習(xí)率的選擇。

數(shù)據(jù)準(zhǔn)備上的變化
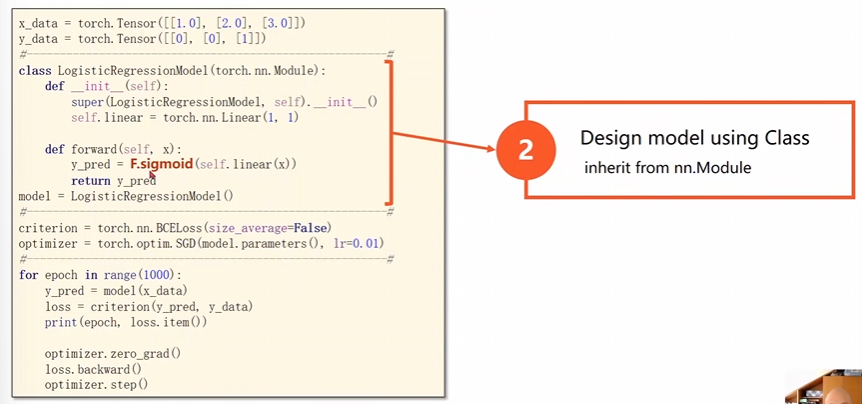


上面就是和之前的線性模型之間的區(qū)別。



 浙公網(wǎng)安備 33010602011771號(hào)
浙公網(wǎng)安備 33010602011771號(hào)