所學(xué)習(xí)的B站視頻鏈接 2 梯度下降算法

0 復(fù)習(xí)

上一次課堂中我們采用了最簡單的線性模型進(jìn)行了嘗試，當(dāng)時我們的輸入維度和輸出的維度均是一維的。

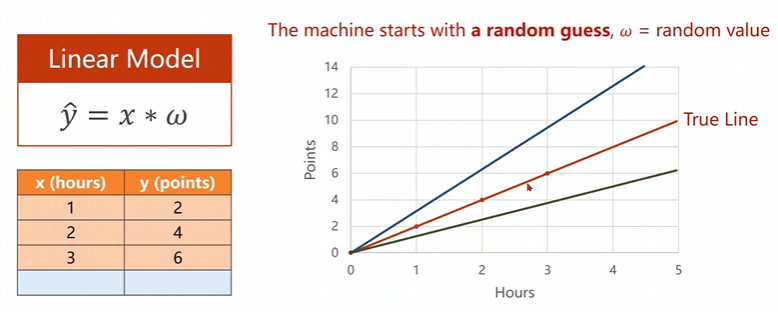
我們隨機猜測我們的權(quán)重，看看什么樣子的權(quán)重是可以讓我們的損失函數(shù)\(MSE\)達(dá)到最小，采用的是一個暴力枚舉法，來得到咱們的曲線。

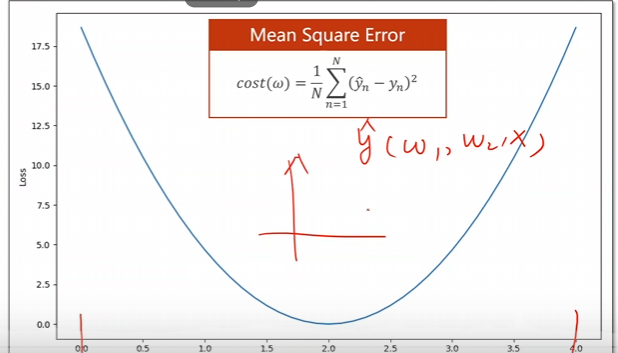
但是這僅僅只是單一權(quán)重的方法，一旦咱們的權(quán)重組合多了，這個時候咱們的程序便非常的難以運行，這個時候需要采用其他的方法和思路進(jìn)行處理。

1 模型原理

1.1 分治思路

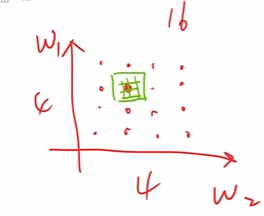
假設(shè)有\(W_1和W_2\)這兩個權(quán)重需要尋找，在進(jìn)行搜索的時候先進(jìn)行一些稀疏的計算，找到可能的最小區(qū)塊，然后在那個區(qū)塊里面進(jìn)行搜索，不斷重復(fù)幾輪即可。

但是這個東西也不一定，因為實際上咱們的真實函數(shù)長得是非常的抽象的，而非普通的凸函數(shù)。上面的那個方法僅僅對比較好的凸函數(shù)才是可以使用的。對于下面這種函數(shù)而言，采用分治法很有可能會錯過一些優(yōu)秀點。

因此需要其他的方法進(jìn)行使用。這種問題就是優(yōu)化問題罷了。

1.2 梯度下降算法

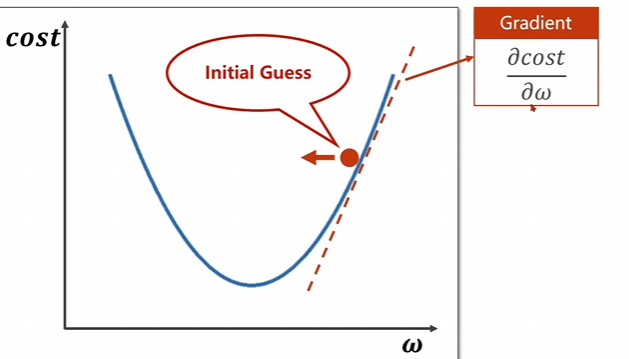
仔細(xì)看上面這個圖片，咱們的紅點是所需要進(jìn)行下降的點，我們需要尋找使得這個點下降的方向，向左還是向右。

對函數(shù)的自變量求偏導(dǎo)，得到的方向是函數(shù)上升的方向，因此我們需要取導(dǎo)數(shù)的一個負(fù)方向進(jìn)行下降，即，

可以看出他一直向著下降速度最快的方向進(jìn)行跑動-貪心，但是這個不一定能找到最優(yōu)解，只能找到一定區(qū)間內(nèi)的局部最優(yōu)點。例如下面這個函數(shù)

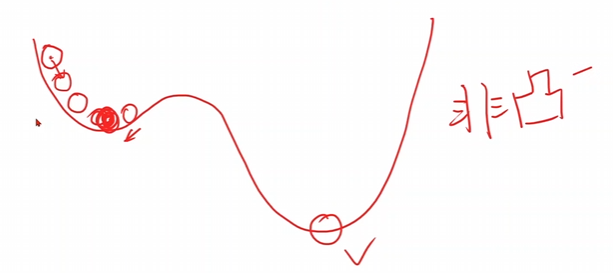
存在很多的局部最優(yōu)點，這個時候采用咱們的梯度下降算法的時候是只能找到局部最優(yōu)點，不能找到全局最優(yōu)點。

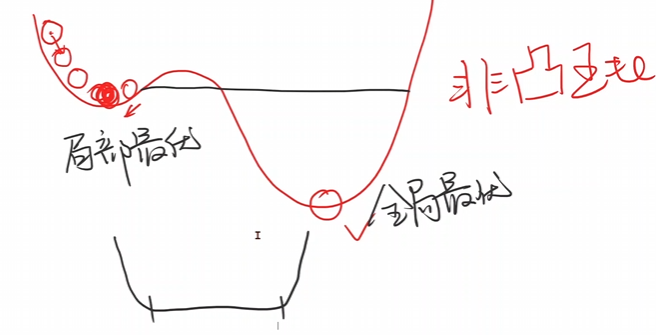
但是實際使用的過程中，咱們在進(jìn)行深度學(xué)習(xí)的過程中，局部最優(yōu)點是比較少的，因此大量的使用梯度下降算法。

但是會存在鞍點也就是所謂的\(f'=0\)的點

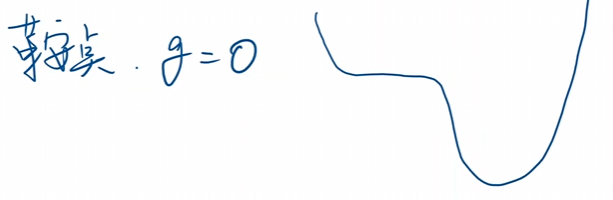
對于這個位置一旦到達(dá)時刻，便會停止迭代，此時會陷入到鞍點無法進(jìn)行運動。畢竟導(dǎo)數(shù)為零了，學(xué)習(xí)率不論是多少都已經(jīng)沒有用了。

可見最大的問題就是鞍點的問題了，我們要盡可能的避免鞍點。

1.3 梯度下降算法的數(shù)學(xué)模型推導(dǎo)

首先先給出上一次課程的損失函數(shù)，咱們用這個函數(shù)進(jìn)行推導(dǎo)

對這個損失函數(shù)進(jìn)行求導(dǎo)可以得到

最后可以求出來咱們的訓(xùn)練過程進(jìn)行更新

這就是咱們的更新函數(shù)\(Update\)

2 代碼編撰

2.1 分塊解答

import numpy as np
import matplotlib.pyplot as plt

引入兩個庫函數(shù)

x_data = [1.0 , 2.0 , 3.0]
y_data = [2.0 , 4.0 , 6.0]

引入需要使用的訓(xùn)練集數(shù)據(jù)

global w
w = 1.0

定義一個猜測，初始化權(quán)重

def forward(x):
    return x*w

定義 \(\hat{y}\) 的公式，令\(\hat{y}=\chi*\omega\)

def cost(xs , ys):
    sum = 0
    for x , y in zip(x_data , y_data):
        sum += forward(x)**2
    return sum/len(xs)

定義這個平均損失函數(shù)\(MSE\)，\(cost(\omega)=\frac{1}{N}\sum_{n=1}^N(\hat{y}_n-y_n)^2\)

def grad(xs , ys):
    sum = 0
    for x , y in zip(xs , ys):
        sum += 2*x*(forward(x) - y)
    return sum/len(xs)

定義這個梯度函數(shù)\(Gradient\)，\(\frac{\partial cost}{\partial\omega}=\frac{1}{N}\sum_{n=1}^N2\cdot x_n\cdot(x_n\cdot\omega-y_n)\)

for epoch in range(100):
    cost_val = cost(x_data , y_data)
    grad_val = grad(x_data , y_data)
    w -= 0.01*grad_val

開始進(jìn)行學(xué)習(xí)擬合處理，\(\omega=\omega-\alpha\frac{\partial cost}{\partial\omega}\)

訓(xùn)練更新的過程，這個\(0.001\)是學(xué)習(xí)率，這個是自己取得，憑感覺把。

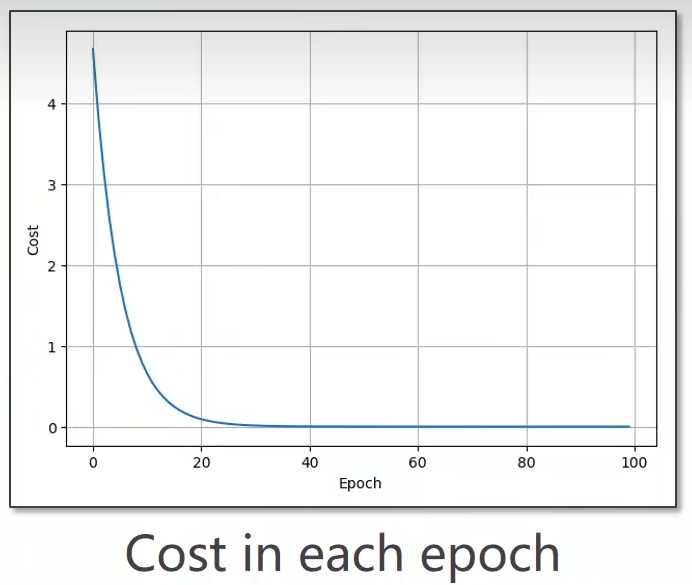
不難看出這個玩意兒是收斂到\(w=2\)的。

只要是總體收斂便就可以了。

當(dāng)然實際上可以采用指數(shù)均值的方式將這個圖像變得更加的平滑。

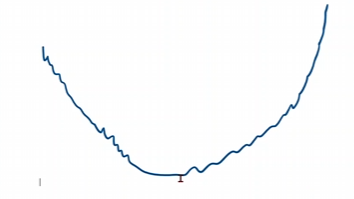
如果你的訓(xùn)練圖像，學(xué)著學(xué)著，成下面這個樣子，那么你就訓(xùn)練失敗了，可以適當(dāng)降低學(xué)習(xí)率。

實際上我們梯度下降用的不多用的是隨機梯度下降多一些。

1. 更新函數(shù)

   • \(Gradient Descent : \omega=\omega-\alpha\frac{\partial cost}{\partial\omega}\)

   • $ Stochastic Gradient Descent : \omega=\omega-\alpha\frac{\partial loss}{\partial\omega}$

2. 梯度求導(dǎo)

   • \(Deribative of Cost Function : \frac{\partial cost}{\partial\omega}=\frac{1}{N}\sum_{n=1}^N2\cdot x_n\cdot(x_n\cdot\omega-y_n)\)

   • \(Derivative of Loss Function : \frac{\partial loss_n}{\partial\omega}=2\cdot x_n\cdot(x_n\cdot\omega-y_n)\)

從里面隨機選擇一個就可以了，就直接拿上單個損失直接用，注意隨機二字

這個有可能可以跨過去鞍點哈，也是有點運氣成分的額。

看看相對于梯度下降而言，這個隨機梯度下降的代碼做了些修改

def loss(x , y):
	y_pred = forward()
    return (y_pred - y)**2

重新計算損失函數(shù)，\(loss=(\hat{y}-y)^{2}=(x*\omega-y)^{2}\)

def grad(x , y)
	return 2 * x * (x*w - y)

重新計算梯度函數(shù)，\(\frac{\partial loss_n}{\partial\omega}=2\cdot x_n\cdot(x_n\cdot\omega-y_n)\)

for epoch in range(100):
    for x,y in zip(x_data ,  y_data):
        gradient = grad(x , y)
		w = w - 0.001 * gradient
        print("\tgradient:" , x , y , gradient)
        l = loss(x , y)

重新進(jìn)行學(xué)習(xí)更新

不過在真正的深度學(xué)習(xí)的過程中，梯度下降中每一個\(f(X_i)\)是相互獨立的，是可以并行求解的。因此他的時間復(fù)雜度低，代碼的效率高。但是由于計算量過大因此性能很低。

但是隨機梯度下降中的\(w\)是從上一個哪來的，前后兩個是由依賴的，算法的效率過低時間復(fù)雜度高，但是他的性能比較高

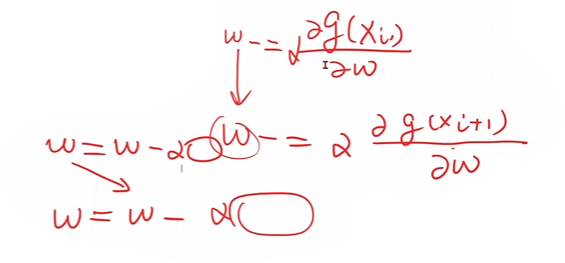
因此我們會使用\(Batch或是Mini-Batch\)進(jìn)行兩種算法的一個這種，一部分進(jìn)行隨機梯度下降，一部分進(jìn)行梯度下降。分組進(jìn)行使用。

2.2 代碼綜合

首先是最原始的梯度下降算法的代碼

'''
@name:  梯度下降算法
'''

import numpy as np
import matplotlib.pyplot as plt

x_data = [1.0 , 2.0 , 3.0 , 4.0]
y_data = [2.0 , 4.0 , 6.0 , 8.0]

w = 1.0

def forward(x):# 前饋相乘求假設(shè)
    global w
    return x*w

def cost(xs , ys):# 計算平均誤差和
    res = 0
    for x,y in zip(xs , ys):
        res += (x*w - y)**2
    res = res /len(xs)
    return res

def gradient(xs , ys):# 求解相應(yīng)的梯度
    sum = 0
    for x , y in zip(xs , ys):
        sum = 2*x*(x*w-y)
    sum = sum/len(xs)
    return sum 

epc_list = []
cos_list = []

for epoch in range(0 , 100 , 1):# 進(jìn)行程序深度學(xué)習(xí)
    epc_list.append(epoch)
    cost_val = cost(x_data , y_data)
    cos_list.append(cost_val)
    grad_val = gradient(x_data , y_data)
    w -= alpha * grad_val

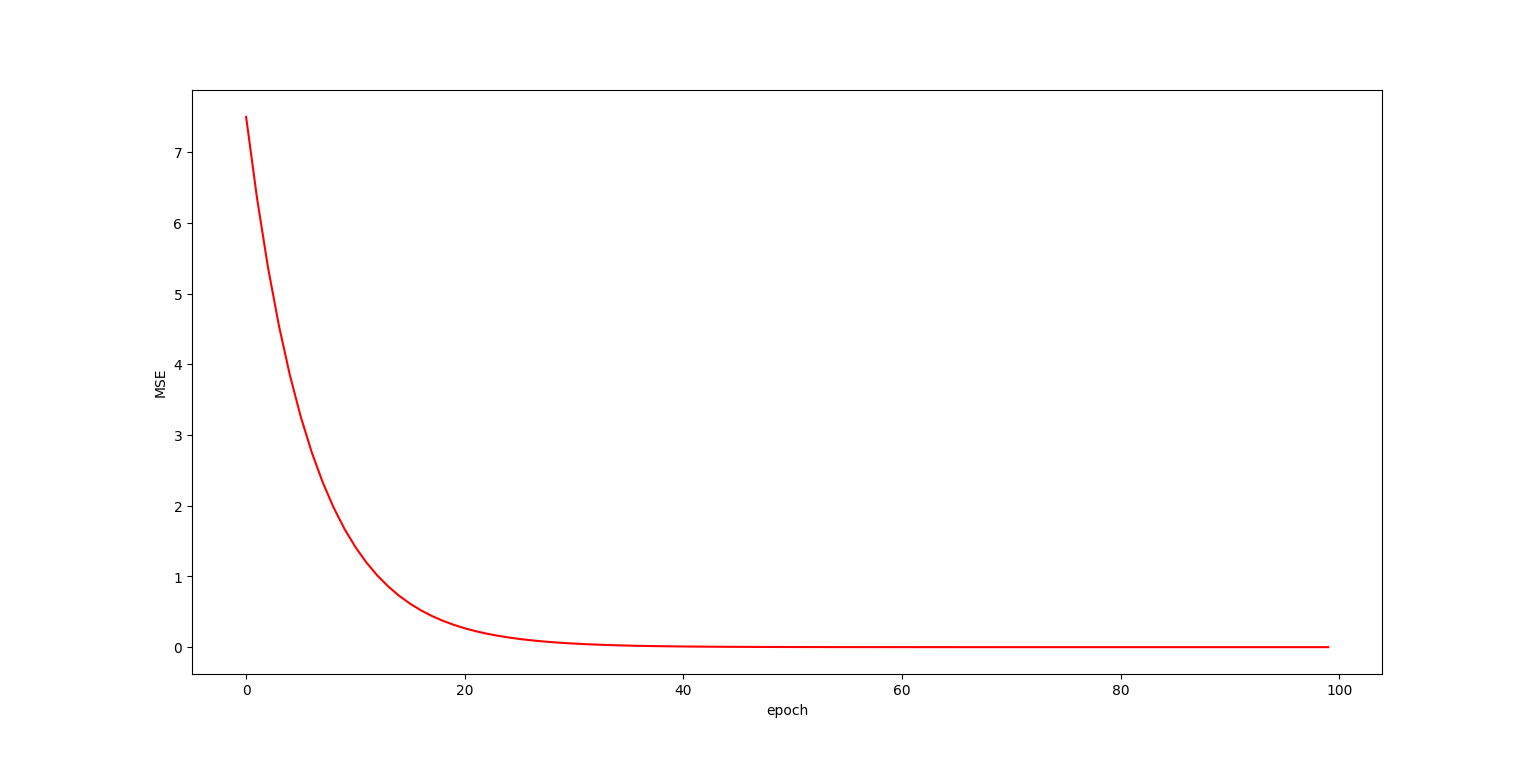
plt.plot(epc_list , cos_list , 'r')
plt.xlabel('epoch')
plt.ylabel('MSE')
plt.show()  

其次是更新后的隨機梯度下降算法的代碼

'''
@name:  隨機梯度下降算法
'''

import numpy as np
import matplotlib.pyplot as plt

def forward(x):# 前饋相乘求假設(shè)
    global w
    return x*w

def loss(x , y):# 計算平均誤差和
    return (forward(x) - y)**2

def gradient(x , y):# 求解相應(yīng)的梯度
    return (2*x*(forward(x) - y))

x_data = [1.0 , 2.0 , 3.0 , 4.0]
y_data = [2.0 , 4.0 , 6.0 , 8.0]

w = 1.0
alpha = 0.01 # learning rate

epc_list = []
loss_list = []
for epoch in range(0 , 100 , 1):# 進(jìn)行程序深度學(xué)習(xí)
    epc_list.append(epoch)
    n = 0.0
    sum = 0.0
    for x,y in zip(x_data ,  y_data):
        n+=1
        grad = gradient(x , y)
        w = w - 0.01 * grad
        l = loss(x , y)
        sum += l
    sum =sum / n
    loss_list.append(sum)

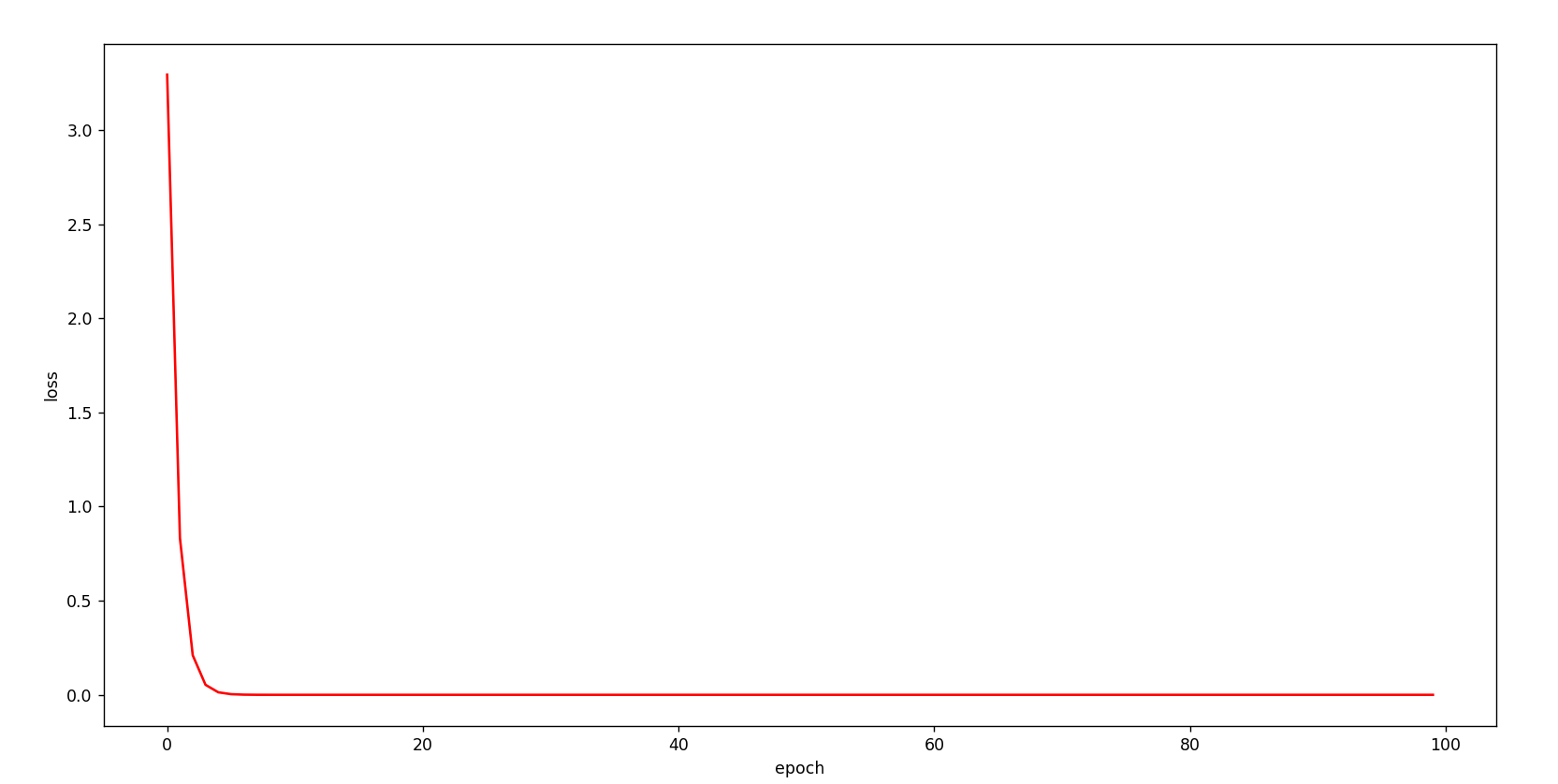
plt.plot(epc_list ,  loss_list , 'r')
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()