3 線性代數
[!IMPORTANT]
B站視頻鏈接05 線性代數動手學深度學習v2
1 線性代數基本知識
1.1 標量
標量在之前的學習過程中便已經知道,只是一些所謂的數據而已,譬如1,2,3之類的單個元素,同我們小時候學習的并無任何的不同。同樣滿足普通數學的四則運算法則,注意哈標量是不帶箭頭的哈!!
現在看一下標量支持的一些普通運算法則
1.1.1 基本運算
普通元素的加法: \(c = a+b\)
普通元素的減法: \(c=a-b\)
普通元素的乘法: \(c = a \times b\)
普通元素的除法: \(c=a \div b\)
1.1.2 長度運算
取絕對值 : \(\left| a \right|=\left\{ \begin{array}{l} a\ \ \ \ \ \ a\ \ge \ 0\\ -a\ \ \ a\ \le 0\\ \end{array} \right.\)
絕對值不等式: \(|a+b| \le |a|+|b|\)
絕對值 乘法:\(|a \cdot b| = |a| \cdot|b|\)
1.2 向量
向量相對于標量而言多了一個維度的空間,向量是一個有方向和長度的東西,而標量只有長度沒有方向,也可以說向量是由許許多多的標量組合而成的。
向量和小時候學習的數據是完全不相同的,它滿足加減但不支持乘除,向量的乘法和除法需要滿足前行后列的要求才可以對應相乘,即向量的內積。
1.2.1 基本運算
- 普通向量的加法:$\vec{c} = \vec{a}+\vec{b} \rightarrow c_i = a_i +b_i $
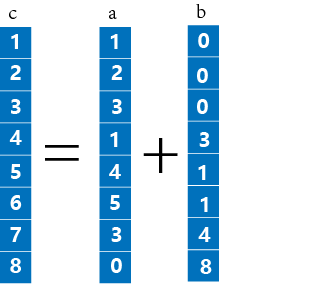
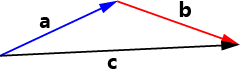
-
普通向量的減法:\(\vec{c} = \vec{a} - \vec{b} \rightarrow c_i = a_i - b_i\) 其表現形式和加法如出一轍便不進行適當的演示了。
-
普通向量的函數:\(\vec{c} = sin \vec{a}\) 這就相當于對向量里面的每一個元素都進行了\(sin\)函數的調用,即\(c_i = sina_i\)
-
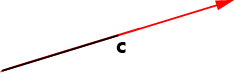
向量和標量的相乘:\(\vec{c} = a \times \vec{\alpha}\) 這就相當于將該向量的長度按照\(a\)倍進行縮放同時不改變其原本向量的方向。
- 向量之間的點乘:\(\vec{\alpha}^T \cdot \vec{\beta} = \sum_{i}{\alpha_i \cdot \beta_i}\) 不難看出向量之間的點乘是有一定要求的這里我們假設向量\(\vec{\alpha} 和 \vec{\beta}\)的形狀均為\(m\)行1列\(即m \times 1\)。現在將\(\vec{\alpha}\)進行轉置則現在他的形狀為\(1 \times m\),此時這兩個向量才可以進行相乘\((1 \times m) \cdot (m \times 1) = 1 \times 1\)最終得到一個單位的數據,這就是向量之間的點乘。
- 向量點乘如果等于零:\(\vec{\alpha}^T \cdot \vec{\beta} =0\),此時可以說明向量\(\vec{\alpha}和向量\vec{\beta}\)相互正交。
1.2.2 長度運算
-
計算長度:\(||\vec{a}||_2 = \sqrt{ \sum_{i=1}^{m} {a_i^2}}\) 也就是對每個元素平方求和后開個方的事情
-
絕對值不等式(也可以說是三角形兩邊之和大于第三邊定理):\(||\vec{a}+\vec{b}|| \le ||\vec{a}||+||\vec{b}||\)
-
絕對值的乘法法則:\(||\vec{a} \cdot \vec{b}|| = ||\vec{a}|| \cdot ||\vec{b}||\)
1.3 矩陣
矩陣是一個非常重要的研究對象對于線性代數而言,同時在考研數學中線性代數主要研究的也是各個矩陣的變換等等,因此矩陣的計算以及研究在深度學習的領域也非常重要的。
在這里我們需要理解,矩陣對于空間變換的影響、矩陣的特征值和特征向量、矩陣的乘法、以及一些特殊矩陣的性質等等問題
1.3.1 基本運算
- 矩陣的加法:\(C = A+B \rightarrow C_{ij} = A_{ij} + B_{ij}\)
- 矩陣的減法:\(C = A-B \rightarrow C_{ij} = A_{ij} - B_{ij}\)
- 矩陣的乘法:$C=A \cdot B \rightarrow \left[ \begin{matrix} C_{11}& C_{12}& C_{13}\ C_{21}& C_{22}& C_{23}\ C_{31}& C_{32}& C_{33} \end{matrix} \right] = \left[ \begin{matrix} A_{11}& A_{12}& A_{13}\ A_{21}& A_{22}& A_{23}\ A_{31}& A_{32}& A_{33} \end{matrix} \right] \cdot \left[ \begin{matrix} B_{11}& B_{12}& B_{13}\ B_{21}& B_{22}& B_{23}\ B_{31}& B_{32}& B_{33} \end{matrix} \right] = \left[ \begin{matrix}
\sum_{i=1}^{3}{A_{1i}\times B_{i1}}&\sum_{i=1}^{3}{A_{1i}\times B_{i2}} &\sum_{i=1}^{3}{A_{1i}\times B_{i3}} \
\sum_{i=1}^{3}{A_{2i}\times B_{i1}}&\sum_{i=1}^{3}{A_{2i}\times B_{i2}} &\sum_{i=1}^{3}{A_{2i}\times B_{i3}} \
\sum_{i=1}^{3}{A_{3i}\times B_{i1}}&\sum_{i=1}^{3}{A_{3i}\times B_{i2}} &\sum_{i=1}^{3}{A_{3i}\times B_{i3}} \
\end{matrix} \right] $ 矩陣乘法遵守前行后列的要求。 - 矩陣的函數:\(C = sinA \rightarrow C_{i j}= sinA_{ij}\)
1.3.2 矩陣性質
- 正交矩陣:\(A\cdot A^T =1\),并且其舉證內部的任意一行均正交
- 特征值和特征向量:\(A\vec{x} = \lambda \vec{x}\),無論矩形A如何進行處理總有一個方向\(\vec{x}\)不會發生方向的變化僅僅只會發生長度的改變。同時實對稱矩陣必定有特征向量。
矩陣這一部分比較難懂因此可以在網絡上面多多學習,我這里推薦知名的數學博主\(3Blue1Brown\)的視頻進行學習
視頻鏈接:[線性代數的本質](【官方雙語/合集】線性代數的本質 - 系列合集_嗶哩嗶哩_bilibili)
2 線性代數的代碼實現
注意下面所有的代碼能夠運行的前提是,自己的計算機已經正確配置好了
pytorch環境,如果環境沒有配置好請一定要耐心配置好后在繼續,環境配置視頻。
環境配置完畢后需要引入自己的庫,下面就不寫這些頭文件了
import torch
import matplotlib.pyplot as plt
import cv2 as cv
import numpy as np

引入成功后便可以進行代碼的編寫啦!
2.1 數組的創建
2.1.1 標量的創建
標量就是一個數字也可以說是一個數據,這個的創建是依托下面的代碼進行實現
x = torch.tensor([3.0]) #創建一個標量x
在編譯器里不難看出他的size僅僅唯1

2.1.2 向量的創建
y = torch.arange(4) #創建一個向量 y
在編譯器中可以看到他的size是4

同時我們可以對向量中各個元素進行適當的索引或是提取的操作
y[0] , y[1] , y[2] , y[3] #逐個提取其中元素
下面是他的數組索引情況,他是從0號開始逐個進行索引的

2.1.3 矩陣的創建
矩陣的創建類型非常的多,可以創建全1的矩陣、全0的矩陣、連續自然數的矩陣等等。
A = torch.ones(20).reshape(4,5) #全1
B = torch.zeros(20).reshape(4,5) #全0
C= torch.arange(20).reshape(4,5) #連續自然數
首先采用函數創建一個比較大的向量,然后將向量的形狀進行修改變成矩陣即可完成創建
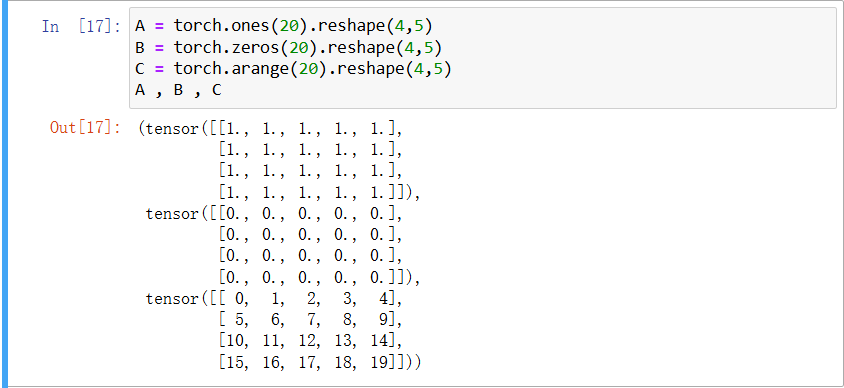
2.2 線性代數的基本運算
2.2.1 標量的基本運算
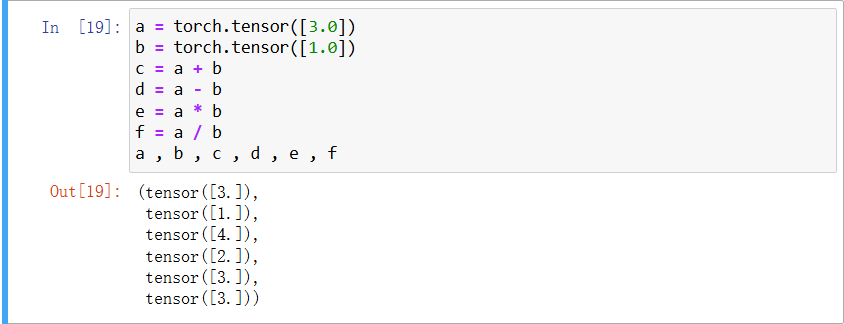
由于標量的基本運算之前已經有過提到因此這次就不詳細的進行說明僅僅將代碼和運行截圖列下。
a = torch.tensor([3.0])
b = torch.tensor([1.0])
c = a + b
d = a - b
e = a * b
f = a / b
2.2.2 向量的點乘
在上面說到,向量的點乘就是兩個長度應該相同的兩個向量進行對應元素相乘后相加,同時要求前一個向量是躺著的,后一個向量是豎著的。
x = torch.arange(5)
y = torch.arange(5)
z = torch.dot(x,y)
x , y , z

如果想要矩陣進行轉置則可以使用下面的代碼命令進行實現
x.T
y.T
z.T
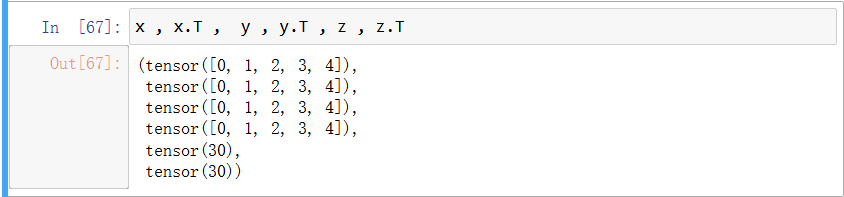
雖然圖片上不大看的出來,但是確實是進行了轉置,可以用矩陣進行查看
C , C.T
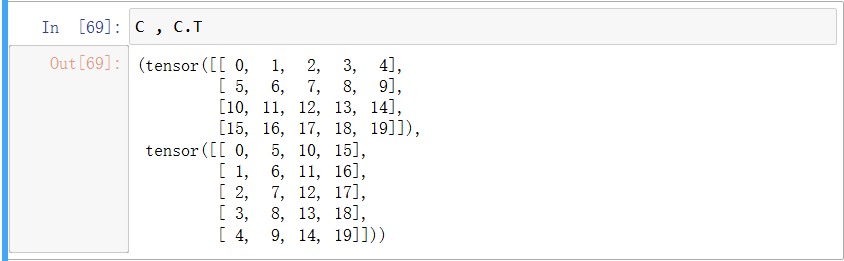
使用矩陣效果就非常的明顯了。
2.2.3 矩陣和向量的乘法
矩陣和向量的乘法主要是下面的這幾個代碼,不過要理解的話需要閱讀相對應的線性代數的教材才可以。
A = torch.arange(12).reshape(3,4)
B = torch.zeros(12).reshape(3,4)
C = torch.tensor([[1,2,3],[9,8,7],[2,5,3],[2,5,6]])
x = torch.arange(4)
y = torch.ones(4)
z = torch.zeros(4)
e1 = torch.mv(A,x)
e2 = torch.mm(A,C)
A , B , C ,x , y , z , e1 ,e2
mm:\(矩陣\times 矩陣\)mv:\(矩陣\times 向量\)
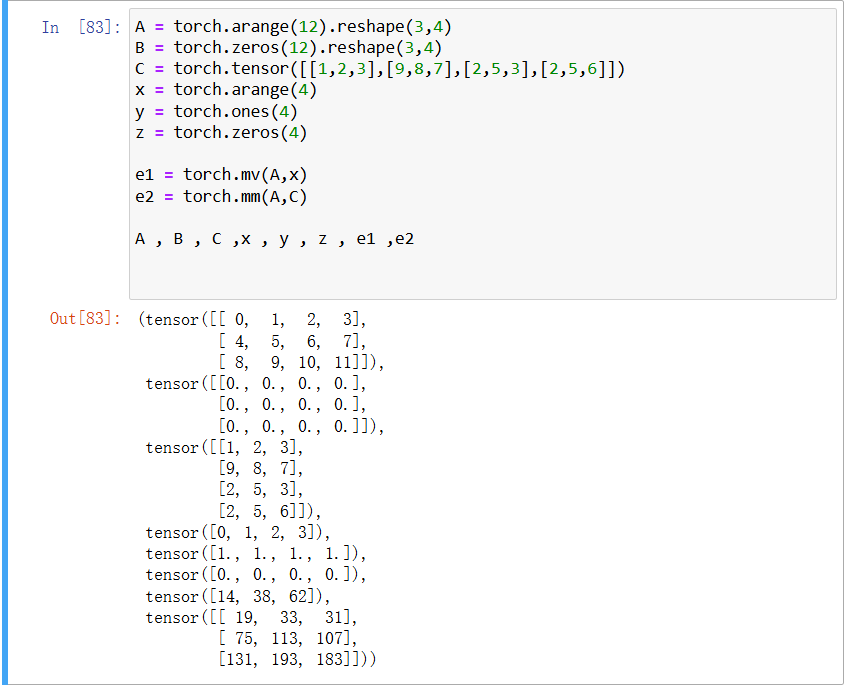
現在基本的一些代碼都已經學的差不多了,現在開始矩陣按照某一固定軸進行求和
2.3 矩陣的按軸求和
矩陣按照固定軸求和,可以看作是空間的壓縮(坍塌)處理,以一個三維的數組為例子
假設有一個數組是一個\(3 \times 8 \times 8\)大小的矩陣,那么他總共有三個軸的方向分別為\(x軸、y軸、z軸\),這三個軸就是所謂的按軸求和的那個軸,我們用圖像來比較直觀的表示一下下。

所謂的\(axis = 0或者axis = 1\)僅僅表示了第幾個軸而已
假設我想要然他按照\(z\)軸進行求和,則和\(z\)軸有關其他直接向著\(z\)軸的方向累加
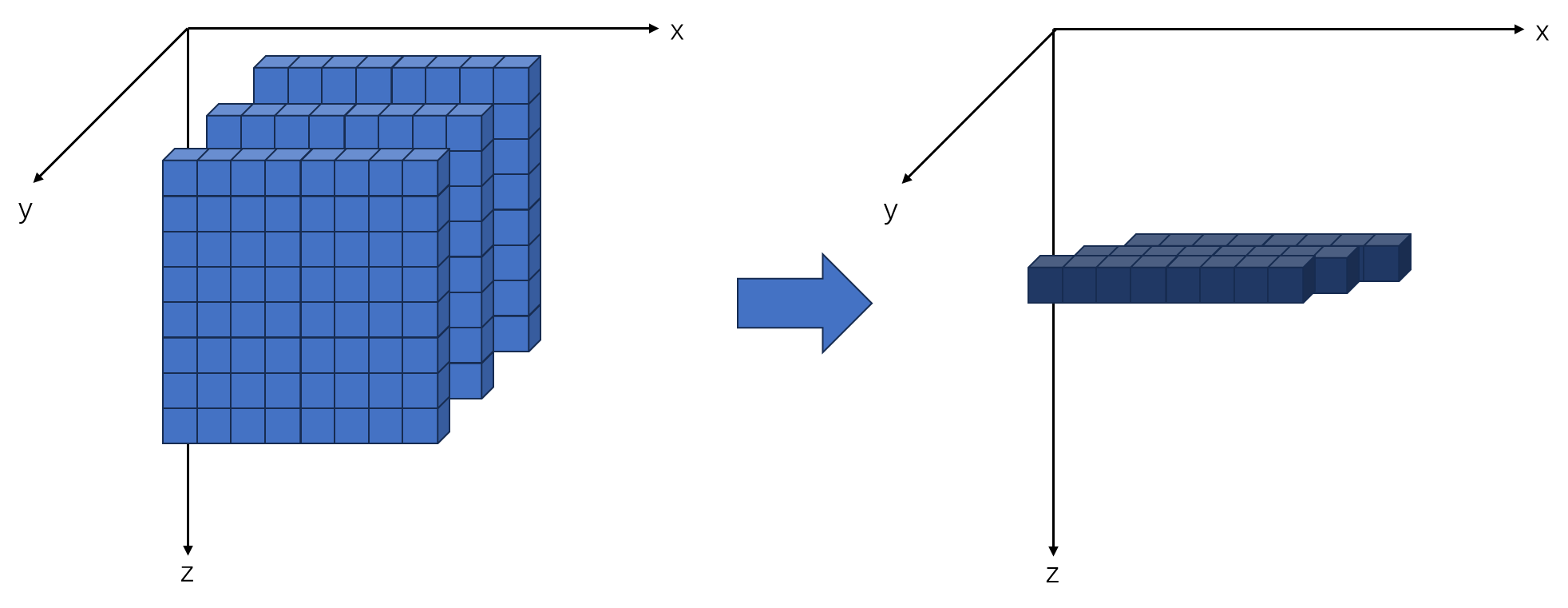
其他的方向也是如此,現在便可以進行代碼的展示
A = torch.arange(24).reshape(2,3,4)
a0 =torch.sum(A,axis = 0)
a1 = torch.sum(A,axis = 1)
a2 = torch.sum(A,axis = 2)
A , a0 , a1 , a2

可以看到情況就是圖片的樣子,按照那個軸進行坍塌,也可以簡單的表示為直接刪去了所求軸的維度。



 浙公網安備 33010602011771號
浙公網安備 33010602011771號