熱傳導方程

問題提出：在三維空間中，考察一均勻、各向同性的物體G，假定其內部有熱源，并且與周圍介質有熱交換，求物體內部溫度的分布和變化規律。

任意一點(x,y,z)在t時刻的溫度為u(x,y,z,t)。

方程推導：

能量守恒定律：物體內部因溫度的變化而吸收的熱量等于通過物體的邊界流入的熱量與由物體內部的熱源所生成的熱量的總和。

取空間中的一個空間微元D，先微分

t=t2時刻的熱量：

 t=t1時刻的熱量：

能量的變化，寫成關于時間t的偏導數的積分。

以下求[t1,t2]時間段通過邊界流入的熱量:

由傅里葉熱傳導定律，即邊界ds的熱量dQ與物體溫度沿曲面的法線方向導數du/dn成正比

積分

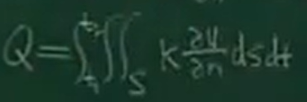
除了外部流入的熱量，還需要求[t1,t2]時間段內部熱源生成的熱量：

設在物體G內熱源的強度為F(x,y,z,t)，則由它生成的熱量為:

由能量守恒，可得：

利用奧高公式，化解可得：

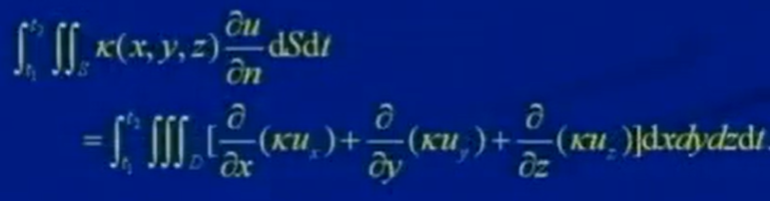
代入上面的能量守恒公式，可得：

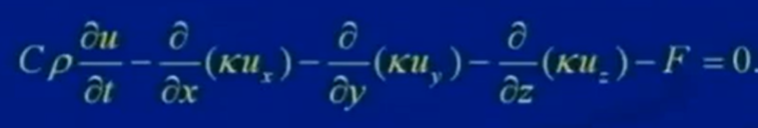
又物體是均勻的且各向同性，則C,ρ,κ都是常數，

令a²=κ/(Cρ), f=F/(Cρ)

則方程可化為

這是帶熱源的三維熱傳導方程。

如果物體內無熱源或熱匯，則方程為：

一維和二維熱傳導方程分別是: