1. 弦振動方程

問題提出：給定一根兩端固定的拉緊的具有彈性的、均勻的、非常柔軟的細線，其長為l, 在外力作用下在平衡位置附近作微小的橫振動，求弦上各點的運動規(guī)律。

基本假設(shè)：
1.密度均勻
2.振動發(fā)生在一個平面，各點位移與平衡位置垂直
3.線是柔軟的，不抵抗彎曲，張力與切線方向一致

方程推導(dǎo)：

動量定理：物體在某-時段內(nèi)的動量的增量等于作用在該物體上所有外力在這一時段內(nèi)產(chǎn)生的沖量。

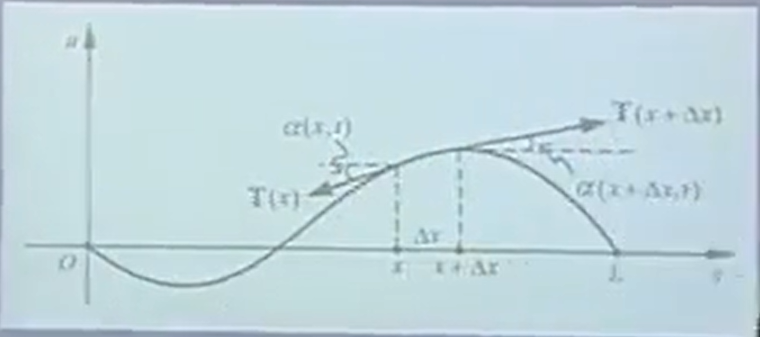
先求某一點的微分，再求整個線的積分。

張力，與時間無關(guān)。所以省略了t，只留下了x。求T(x)與T(x+Δx)的關(guān)系。

彈簧在每一點的張力大小與時間t無關(guān)，只與相鄰的點之間的分子距離有關(guān)。被拉的越長，張力就越大。

按照胡克定律，一根長l的繩子，被拉伸了l+Δl。

已知y=y(x)是光滑曲線，求弧長ds。參考：

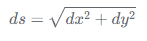
由于y是x的函數(shù)，即y=y(x)，那么dy = y'(x) dx。因此，代入上式：

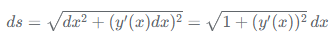
 由微弧長ds，可得某一段的弧長s。

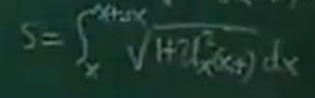
張力分為兩個方向的力：x方向和y方向。

假設(shè)，平行方向x的力不存在，只存在垂直于x方向的y方向的力。

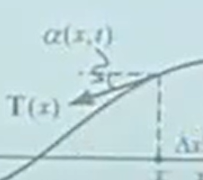
 力的分解。

可以寫成

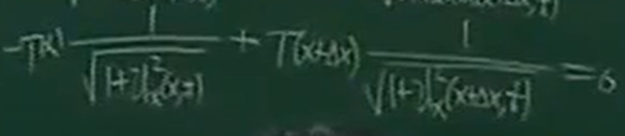
T(x)=T(x+Δx)

現(xiàn)在計算微弦段[x,x+Δx]上，t+△t 時刻的動量：

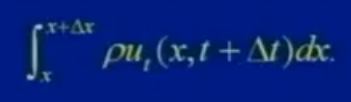
∫(密度*速度)dx

速度是指單位長度的切線速度還是垂直方向的速度？不重要，因為水平速度積分是肯定為0。

在t時刻的動量：

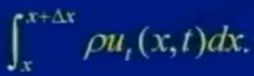
 根據(jù)動量定理，t+Δt時刻的動量減去t時刻的動量：

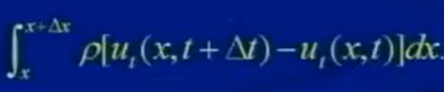
(繩子)動量的變化=(外界)垂直方向的作用力*Δt

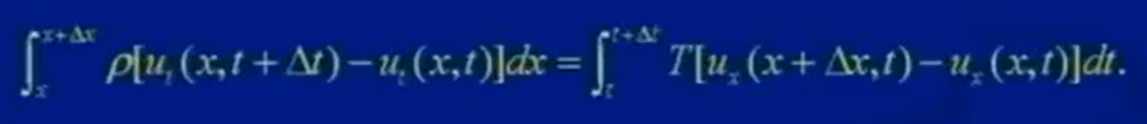
得

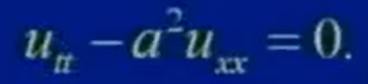
以上方程被稱為一維波動方程，類似地可導(dǎo)出二維波動方程和三維波動方程，它們的形式分別為：

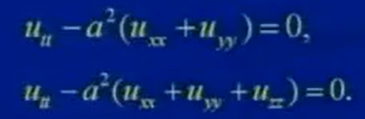
二維波動方程是指一個平面上的震動。

三維波動方程是指聲音在三維空間中的傳播。可以布滿整個三維空間。