[C#] 使用 .NET 的跨平臺SIMD硬件加速功能，將 GEMM（通用矩陣乘法）算法速度提升1080倍，比肩 MKL、OpenBLAS

GEMM（General Matrix Multiply，通用矩陣乘法）是科學計算與深度學習等領域的核心算法。以前用 C# 開發的GEMM程序的性能，比MKL、OpenBLAS差得遠，這是因為那時的 .NET 不支持SIMD硬件加速技術。從2014年開始， .NET 對SIMD硬件加速技術的支持越來越完善了。我潛心研究用該技術來改進 C# GEMM程序的性能，最近有了重大突破——對于1024尺寸矩陣的SGEMM，我的算法比基礎算法的性能提升1080倍，與 MKL、OpenBLAS的測試結果在同一梯隊。

[C#] 使用 .NET 的跨平臺SIMD硬件加速技術，將 GEMM（通用矩陣乘法）程序性能提升1080倍，比肩 MKL、OpenBLAS

GEMM（General Matrix Multiply，通用矩陣乘法）是科學計算與深度學習等領域的核心算法。GEMM的性能越高，對科學計算與深度學習等領域的促進作用越大。對于CPU做GEMM運算，Intel MKL（Math Kernel Library。后面將統一簡稱為 MKL）、OpenBLAS 是第一梯隊的行業翹楚。它們使用了并行、SIMD指令集、手動匯編優化等優化技術，使性能達到行業頂尖水平。

以前用 C# 開發的GEMM程序的性能，比MKL、OpenBLAS差得遠，這是因為那時的 .NET 不支持SIMD硬件加速技術。從2014年開始， .NET 對SIMD硬件加速技術的支持越來越完善了。我潛心研究用該技術來改進 C# GEMM程序的性能，最近有了重大突破——對于1024尺寸矩陣的SGEMM（Single General Matrix Multiply，單精度浮點數通用矩陣乘法），我的算法比基礎算法的性能提升1080倍，與 MKL、OpenBLAS的測試結果在同一梯隊。

它是純 C# 編寫的托管代碼程序，同一套源代碼能在 X86、Arm 等架構上運行，性能均能達到第一梯隊的水平。而且該算法能很容易地改造為DGEMM（Double General Matrix Multiply，雙精度浮點數通用矩陣乘法）運算——因巧妙利用了 using指令，只用復制（SGEMM的）源代碼，無需修改。

MKL 版本：2022.0.0.115
OpenBLAS 版本：2025.1.13

一、基本算法與測試辦法

1.1 矩陣乘法的定義

通用矩陣乘法（General Matrix Multiply，GEMM）是計算兩個矩陣 A 和 B 的乘積 C 的運算，要求 A 的列數等于 B 的行數。假設：

A 是 M * K 矩陣（M 行，K 列），
B 是 K * N 矩陣（K 行，N 列），
則乘積 C = A * B 是 M * N 矩陣，其中每個元素 $C_{i,j}$ 為：$C_{i,j} = \sum_{k=1}^K A_{i,k} \cdot B_{k,j}$。即 A 的第 i 行與 B 的第 j 列的點積。

MultiplyMatrix_basic

1.1.1 矩陣形狀與運算復雜度

時間復雜度：O(M * N * K)，共需 M * N * K 次乘法和加法運算。
空間復雜度：輸入矩陣需 O(M * K + K * N) 存儲空間，輸出矩陣需 O(M * N)。

若 M、N、K 都相同，即 A、B、C都是 N*N 的方陣時——

時間復雜度：O(N^3)，共需 N^3 次乘法和加法運算。
空間復雜度：輸入矩陣需 O(2 * N^2) 存儲空間，輸出矩陣需 O(N^2)。

當 N 為 1024時，乘法總次數為：1024^3 = 1073741824 = 1 Giga。

浮點運算總次數是N^3 次乘法和加法運算，即 2 * 1024^3 = 2 * 1073741824 = 2 Giga。

此時（ N 為 1024時）可以比較方便的算出每秒浮點運算次數 GFOPS (Giga Floating-point Operations Per Second)。假設程序耗時為 t 秒(s)，那么它每秒浮點運算次數為——

每秒浮點運算次數 = 浮點運算總次數 / 耗時 = 2 / t (GFOPS)

1.2 C++ 開發的矩陣乘法最基礎實現

根據上面的矩陣乘法定義，可以編程實現它。例如用 C++ 開發的矩陣乘法最基礎實現如下。

void gemmVanilla(const std::vector<float> &matA, const std::vector<float> &matB,
  std::vector<float> &matC, size_t matSize) {
  // Clear matC.
  for (size_t i = 0; i < matC.size(); i++) {
    matC[i] = 0;
  }

  // Matrix matrix multiply.
  for (size_t i = 0; i < matSize; i++) {
    for (size_t j = 0; j < matSize; j++) {
      size_t cIdx = i * matSize + j;
      for (size_t k = 0; k < matSize; k++) {
        size_t aIdx = i * matSize + k;
        size_t bIdx = k * matSize + j;
        matC[cIdx] += matA[aIdx] * matB[bIdx];
      }
    }
  }
}

這段代碼出自【深緩中字】為什么6層嵌套循環讓這個算法快了120倍？。這個視頻是學習矩陣算法優化的優秀教程，推薦讀者觀看。

這段代碼使用 std::vector<float> 類型來傳遞矩陣數據。雖然 std::vector<float> 本身僅能存儲一維數據，而這段代碼隱式約定了其存儲了 matSize * matSize 個數據，正好是二維的矩陣數據。由于 std::vector<float> 是線性存儲數據的，所以此時存儲的矩陣，可看作行主序的矩陣。

這段代碼的開頭做了“清除矩陣C”（Clear matC）的工作。隨后按照矩陣乘法定義，編寫3層循環，實現了矩陣乘法的功能。

1.3 C# 開發的矩陣乘法最基礎實現（Basic）

1.3.1 矩陣乘法的實現

將上述代碼由 C++ 轉為 C# 語言，便能得到 C# 版矩陣乘法。見下面的 StaticBasic 方法。

// My type.
using TMy = Single;

partial class MultiplyMatrixStatic {

    /// <summary>
    /// Basic on Array.
    /// </summary>
    /// <param name="M">The number of rows in matrix A (矩陣A的行數).</param>
    /// <param name="N">The number of columns in matrix B (矩陣B的列數).</param>
    /// <param name="K">The number of columns in matrix A, or the number of rows in matrix B (矩陣A的列數, 或矩陣B的行數).</param>
    /// <param name="A">Matrix A.</param>
    /// <param name="strideA">Stride of A.</param>
    /// <param name="B">Matrix B.</param>
    /// <param name="strideB">Stride of B.</param>
    /// <param name="C">Matrix C.</param>
    /// <param name="strideC">Stride of C.</param>
    public static void StaticBasic(int M, int N, int K, TMy[] A, int strideA, TMy[] B, int strideB, TMy[] C, int strideC) {
        // Matrix multiply.
        for (int i = 0; i < M; ++i) {
            for (int j = 0; j < N; ++j) {
                int cIdx = i * strideC + j;
                C[cIdx] = 0;
                for (int k = 0; k < K; ++k) {
                    int aIdx = i * strideA + k;
                    int bIdx = k * strideB + j;
                    C[cIdx] += A[aIdx] * B[bIdx];
                }
            }
        }
    }
}

上述代碼位于 MultiplyMatrixStatic.Single.cs.

C# 版代碼做了3個改造——

使用using語句定義了別名（using TMy = Single）。這能便于將代碼改造為DGEMM（Double General Matrix Multiply，雙精度浮點數通用矩陣乘法），那時僅需將 TMy指向Double類型就行。
簡化了代碼。移除了“清除矩陣C”（Clear matC）的工作，改為每次在 j 循環時將C矩陣的對應元素清零。
修改了函數參數列表，參考 BLAS(Basic Linear Algebra Subprograms)的sgemm函數的參數列表。明確傳遞了 M、N、K 這3種尺寸參數，便于支持非方形的矩陣。且明確傳遞了各個矩陣的跨距（strideA），它類似 sgemm函數的 lda參數。

參數說明——

M：矩陣A和矩陣C的行數.
N：矩陣B和矩陣C的列數.
K：矩陣A和矩陣B的列數.
A：矩陣A. 即左矩陣.
strideA：矩陣A每一行的跨距.
B：矩陣B. 即右矩陣.
strideB ：矩陣B每一行的跨距.
C：矩陣C. 即結果矩陣.
strideC：矩陣C每一行的跨距.

由于二維數組的性能比較差，于是這里使用了一維數組（TMy[]）。隨后像 C++ 代碼那樣，手動計算索引，從而實現了對二維矩陣數據的計算。

1.3.2 基準測試方法

本文統一使用 BenchmarkDotNet 做基準測試。

對于上面的StaticBasic方法，它的基準測試代碼如下。

[Benchmark(Baseline = true)]
public void Basic() {
    StaticBasic(MatrixM, MatrixN, MatrixK, arrayA!, StrideA, arrayB!, StrideB, arrayC!, StrideC);
    if (CheckMode) {
        dstTMy = GetCheckSum();
        baselineTMy = dstTMy;
        BenchmarkUtil.WriteItem("# Basic", string.Format("{0}", baselineTMy));
    }
}

上述代碼位于 MatrixNMultiplyBenchmark_Single.cs.

該方法內的第一行，調用了StaticBasic方法，從而實現了對它基準測試。MatrixM, MatrixN, MatrixK, arrayA 等參數都是事先初始化好的，這樣能避免每次重新分配帶來的開銷。

后面的 CheckMode 分支，是在做矩陣運算結果檢查。得益于現代CPU的分支預測能力，該分支不會影響基準測試。讀者若對矩陣運算結果檢查或arrayA初始化感興趣的話，可自行查閱相關源代碼。

注：本項目開啟了可空引用檢查（Nullable），因arrayA等數組可能為空，若直接使用會有警告，但其實這些數組已經做好初始化了。于是可以在數組變量后面加“!”（感嘆號），提醒編譯器此時數組已經非空，以此消除警告。

1.4 增加MathNet、MKL、OpenBLAS的基準測試

本程序還引入了下列矩陣運算庫，用于做基準測試成績的對比。

MathNet 版本：6.0.0-beta2
OpenBLAS 版本：2025.1.13
MKL 版本：2022.0.0.115

1.4.1 引入庫

在 nuget.org 上，可以找到這些庫的 C# 包。

MathNet：使用“MathNet.Numerics”包。它由托管代碼組成，支持在各種CPU架構、各種操作系統上運行。
MKL：使用“MKL.NET”等包。它僅提供了X86架構的原生動態庫，支持在 Windows、MacOS等操作系統。
OpenBLAS：使用“OpenBlasSharp”等包。雖然OpenBLAS支持多種CPU架構，但該包僅提供了X86架構、Windows平臺的原生動態庫。

雖然使用 Visual Studio 的 Nuget包管理功能可以添加這些包，但原生動態庫僅支持部分平臺。為了跨平臺測試方便，于是我在 MatrixBenchmarkCs.csproj 里編寫了條件分支來引入這些包。

<PropertyGroup Condition=" '$(ExUseNativeDll)' == '' AND '$(TargetFramework)' == 'net9.0' AND '$(OS)' == 'Windows_NT' ">
    <ExUseNativeDll>true</ExUseNativeDll>
</PropertyGroup>
<PropertyGroup Condition="'$(ExUseNativeDll)' == ''">
    <ExUseNativeDll>false</ExUseNativeDll>
</PropertyGroup>
<PropertyGroup Condition="'$(ExUseNativeDll)' == 'true'">
    <DefineConstants>$(DefineConstants);USE_NATIVE_DLL</DefineConstants>
</PropertyGroup>
<ItemGroup Condition="'$(ExUseNativeDll)' == 'true'">
    <PackageReference Include="MKL.NET" Version="$(MKLNETVersion)" />
    <PackageReference Include="OpenBlasSharp" Version="$(OpenBlasSharpVersion)" />
</ItemGroup>
<Choose>
    <When Condition=" '$(ExUseNativeDll)' == 'true' AND '$(OS)' == 'Windows_NT' ">
        <ItemGroup>
            <PackageReference Include="MKL.NET.win-x64" Version="$(MKLNETwinx64Version)" />
            <PackageReference Include="OpenBlasSharp.Windows" Version="$(OpenBlasSharpWindowsVersion)" />
            <!--
            <PackageReference Include="MKL.NET.win-86" Version="$(MKLNETwinx64Version)" />
            -->
        </ItemGroup>
    </When>
    <When Condition=" '$(ExUseNativeDll)' == 'true' AND '$([System.Runtime.InteropServices.RuntimeInformation]::IsOSPlatform($([System.Runtime.InteropServices.OSPlatform]::Linux)))' ">
        <ItemGroup>
            <PackageReference Include="MKL.NET.linux-x64" Version="$(MKLNETlinuxx64Version)" />
        </ItemGroup>
    </When>
    <When Condition=" '$(ExUseNativeDll)' == 'true' AND '$([System.Runtime.InteropServices.RuntimeInformation]::IsOSPlatform($([System.Runtime.InteropServices.OSPlatform]::OSX)))' ">
        <ItemGroup>
            <PackageReference Include="MKL.NET.osx-x64" Version="$(MKLNETosxx64Version)" />
        </ItemGroup>
    </When>
    <Otherwise>
    </Otherwise>
</Choose>

上面配置為——僅 .NET 9.0、Windows操作系統時，才使用原生動態庫。若你想在其他平臺上測試，可以修改 <ExUseNativeDll>false</ExUseNativeDll> 中的值。將它改為“true”。

版本號是在 Directory.Build.props 里定義的。

<MathNetNumericsVersion>6.0.0-beta2</MathNetNumericsVersion>

<MKLNETVersion>1.6.0</MKLNETVersion>
<MKLNETwinx64Version>2022.0.0.115</MKLNETwinx64Version>
<MKLNETlinuxx64Version>2022.0.1.117</MKLNETlinuxx64Version>
<MKLNETosxx64Version>2022.0.0.105</MKLNETosxx64Version>

<OpenBlasSharpVersion>0.3.4</OpenBlasSharpVersion>
<OpenBlasSharpWindowsVersion>2025.1.13</OpenBlasSharpWindowsVersion>

1.4.2 這些庫的基準測試方法

1.4.2.1 MathNet的基準測試方法（UseMathNet）

由于 MathNet 的矩陣運算函數不直接支持數組，而需要用它提供的矩陣類型。于是按它要求，定義了相關變量，并進行了初始化。

protected MathNet.Numerics.LinearAlgebra.Matrix<TMy>? matA;
protected MathNet.Numerics.LinearAlgebra.Matrix<TMy>? matB;
protected MathNet.Numerics.LinearAlgebra.Matrix<TMy>? matC;

protected override void GlobalSetupCore() {
    base.GlobalSetupCore();
    try {
        matA = MathNet.Numerics.LinearAlgebra.Matrix<TMy>.Build.DenseOfRowMajor(MatrixM, MatrixK, arrayA);
        matB = MathNet.Numerics.LinearAlgebra.Matrix<TMy>.Build.DenseOfRowMajor(MatrixK, MatrixN, arrayB);
        matC = MathNet.Numerics.LinearAlgebra.Matrix<TMy>.Build.Dense(MatrixM, MatrixN);
    } catch (Exception ex) {
        BenchmarkUtil.WriteItem("# Setup-error", string.Format("{0}", ex.Message));
    }
}

MathNet的基準測試的方法如下。

[Benchmark]
public void UseMathNet() {
    //MathNet.Numerics.Control.UseMultiThreading(); // Default is UseMultiThreading.
    matA!.Multiply(matB, matC);
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("UseMathNet");
    }
}

//[Benchmark]
public void UseMathNetSingleThread() {
    MathNet.Numerics.Control.UseSingleThread();
    matA!.Multiply(matB, matC);
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("UseMathNet");
    }
}

使用Matrix類型的Multiply方法進行矩陣乘法運算。

注意 MathNet 默認是執行多線程運算的。若想對比 MathNet的單線程時的性能，可以將UseMathNetSingleThread中 //[Benchmark] 的注釋移除，并將UseMathNet中 //MathNet.Numerics.Control.UseMultiThreading 的注釋移除。測試后會發現 UseMathNetSingleThread的成績很差，且多線程的UseMathNet的性能也下降了。應該是 MathNet.Numerics.Control.UseMultiThreading 開銷比較大，故本程序注釋了UseMathNetSingleThread方法，僅測試多線程，不用切換。

由于 MathNet 的矩陣運算函數不直接支持數組，而是需要用它提供的矩陣類型，使用繁瑣。CheckMode分支目前其實是不起作用的。因我們重點是做性能的基準測試，可忽略這一點。

1.4.2.2 OpenBLAS的基準測試方法（UseOpenBLAS）

OpenBLAS的基準測試的方法如下。

[Benchmark]
public unsafe void UseOpenBLAS() {
    fixed (TMy* pA = &arrayA![0], pB = &arrayB![0], pC = &arrayC![0]) {
        OpenBlasSharp.Blas.Sgemm(OpenBlasSharp.Order.RowMajor, OpenBlasSharp.Transpose.NoTrans, OpenBlasSharp.Transpose.NoTrans, MatrixM, MatrixN, MatrixK, 1, pA, StrideA, pB, StrideB, 0, pC, StrideC);
    }
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("UseOpenBLAS");
    }
}

使用該庫的Sgemm方法進行矩陣乘法運算。因它僅支持原生指針參數，于是需要使用 fixed 關鍵字來獲取原生指針。

1.4.2.3 MKL的基準測試方法（UseMKL）

MKL的基準測試的方法如下。

[Benchmark]
public void UseMKL() {
    MKLNET.Blas.gemm(MKLNET.Layout.RowMajor, MKLNET.Trans.No, MKLNET.Trans.No, MatrixM, MatrixN, MatrixK, 1, arrayA!, StrideA, arrayB!, StrideB, 0, arrayC!, StrideC);
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("UseMKL");
    }
}

使用該庫的gemm方法進行矩陣乘法運算。它支持數組參數，使用簡單。

1.4.3 目前的基準測試結果

我的CPU是 “AMD Ryzen 7 7840H”，操作系統是 “Windows 11”。對于 1024 * 1024 矩陣的SGEMM，目前的基準測試結果如下。

BenchmarkDotNet v0.15.2, Windows 11 (10.0.26100.4946/24H2/2024Update/HudsonValley)
AMD Ryzen 7 7840H w/ Radeon 780M Graphics 3.80GHz, 1 CPU, 16 logical and 8 physical cores
.NET SDK 9.0.301
  [Host]    : .NET 9.0.6 (9.0.625.26613), X64 AOT AVX-512F+CD+BW+DQ+VL+VBMI
  MediumRun : .NET 9.0.6 (9.0.625.26613), X64 RyuJIT AVX-512F+CD+BW+DQ+VL+VBMI

Method	N	Mean	Error	StdDev	Median	Ratio	RatioSD	Code Size
Basic	1024	4,712,905,103.3 ns	35,792,824.68 ns	53,573,019.05 ns	4,722,569,850.0 ns	1.000	0.02	954 B
UseMathNet	1024	53,205,723.8 ns	836,527.21 ns	1,226,170.84 ns	52,803,610.0 ns	0.011	0.00	7,575 B
UseOpenBLAS	1024	2,932,070.9 ns	117,359.68 ns	160,643.26 ns	2,864,316.2 ns	0.001	0.00	NA
UseMKL	1024	4,379,927.2 ns	58,880.02 ns	88,128.84 ns	4,340,348.8 ns	0.001	0.00	508 B

Basic 耗時4,712,905,103.3 ns，即 4.7 秒左右。而最快的UseOpenBLAS僅需 2,932,070.9 ns，即0.0029 秒左右，快了很多倍。

對測試結果進行仔細對比——

Basic: 耗時 4,712,905,103.3 ns, 故 GFOPS 為 2 / 4.7129051033 ≈ 0.42.
UseMathNet: 耗時 53,205,723.8 ns, 故 GFOPS 為 2 / 0.0532057238 ≈ 37.59, 性能是Basic的 4,712,905,103.3 / 53,205,723.8 ≈ 88.58 倍.
UseOpenBLAS: 耗時 2,932,070.9 ns, 故 GFOPS 為 2 / 0.0029320709 ≈ 682.11, 性能是Basic的 4,712,905,103.3 / 2,932,070.9 ≈ 1607.36 倍.
UseMKL: 耗時 4,379,927.2 ns, 故 GFOPS 為 2 / 0.0043799272 ≈ 456.63, 性能是Basic的 4,712,905,103.3 / 4,379,927.2 ≈ 1076.02 倍.

可以看到，基礎算法比起MKL、OpenBLAS，有上千倍的性能差距。雖然差距大，但這也表示優化的空間很大。

二、標量算法優化

首先可以在標量算法的范疇內，多多考慮優化辦法。

2.1 循環順序由ijk改為ikj（TileRow）

對于矩陣乘法，有一種簡單且實用的優化辦法，它就是——循環順序由ijk改為ikj。

這么簡單的辦法真的有效嗎？實際測試一下就知道了。

2.1.1 算法的實現

public static void StaticTileRow(int M, int N, int K, TMy[] A, int strideA, TMy[] B, int strideB, TMy[] C, int strideC) {
    // Clear matrix C.
    //C.AsSpan().Clear();
    MatrixUtil.Fill((TMy)0, M, N, C, strideC);
    // Matrix multiply.
    for (int i = 0; i < M; ++i) {
        for (int k = 0; k < K; ++k) {
            int aIdx = i * strideA + k;
            for (int j = 0; j < N; ++j) {
                int bIdx = k * strideB + j;
                int cIdx = i * strideC + j;
                C[cIdx] += A[aIdx] * B[bIdx];
            }
        }
    }
}

因現在循環順序由ijk改為ikj，導致循環內不適合做 C矩陣元素的清零。于是需要在循環前對C矩陣整體做清零處理。

2.1.1.1 矩陣清零

對數組做清零處理，目前最方便的辦法是將數組轉為Span，再執行Clear方法。即 C.AsSpan().Clear()。

考慮到這個參數具有 strideC 參數，應根據該參數的含義，僅對范圍內的數據執行清零。于是我寫了一個工具方法 “MatrixUtil.Fill”來實現該功能，源代碼如下。

/// <summary>
/// Fill value (填充值).
/// </summary>
/// <typeparam name="T">The element type (元素的類型).</typeparam>
/// <param name="value">The value (值).</param>
/// <param name="rows">The number of rows in matrix (矩陣的行數).</param>
/// <param name="cols">The number of columns in matrix (矩陣的列數).</param>
/// <param name="matrix">The matrix (矩陣).</param>
/// <param name="stride">The stride of matrix. When it is 0, use cols (矩陣的跨距. 為 0 時 使用 cols).</param>
/// <param name="start">The start index of matrix (矩陣的開始索引).</param>
public static void Fill<T>(T value, int rows, int cols, Span<T> matrix, int stride = 0, int start = 0) {
    if (0 == stride) {
        stride = cols;
    }
    int idx0 = start;
    for (int i = 0; i < rows; i++) {
        Span<T> span = matrix.Slice(idx0, cols);
        span.Fill(value);
        // Next.
        idx0 += stride;
    }
}

這個工具函數，是逐行對數組進行處理的。對于每一行的內容，轉為Span做清零處理。當一行處理完畢時，會根據stride參數移動到下一行的起始索引。

2.1.2 基準測試方法

對于上面的方法，它的基準測試代碼如下。

[Benchmark]
public void TileRow() {
    StaticTileRow(MatrixM, MatrixN, MatrixK, arrayA!, StrideA, arrayB!, StrideB, arrayC!, StrideC);
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("TileRow");
    }
}

2.1.3 基準測試結果

基準測試結果如下。

Method	N	Mean	Error	StdDev	Median	Ratio	RatioSD	Code Size
Basic	1024	4,712,905,103.3 ns	35,792,824.68 ns	53,573,019.05 ns	4,722,569,850.0 ns	1.000	0.02	954 B
TileRow	1024	780,626,575.0 ns	5,970,550.33 ns	8,562,785.59 ns	778,917,250.0 ns	0.166	0.00	1,238 B

對測試結果進行對比——

Basic: 耗時 4,712,905,103.3 ns, 故 GFOPS 為 2 / 4.7129051033 ≈ 0.42.
TileRow: 耗時 780,626,575.0 ns, 故 GFOPS 為 2 / 0.7806265750 ≈ 2.56, 性能是Basic的 4,712,905,103.3 / 780,626,575.0 ≈ 6.04 倍.

簡單來說，耗時從 4.7 秒，降低到 0.77 秒左右，速度提升了6.09倍。而改變僅是“循環順序由ijk改為ikj”。

2.2 性能為什么會有這么大提升呢？

有些讀者可能會疑惑——只是調換循環次序，甚至多了矩陣清零操作，性能為什么會有這么大提升呢？

現在來仔細分析一下。

2.2.1 循環次序ijk（Basic）

Basic算法的循環次序是ijk，即它的最內層循環是k的循環。此時分析一下3個矩陣的數據訪問情況。

A（左矩陣）：優。最內層循環每處理一次，A的索引僅需+1，是連續的內存訪問。
B（右矩陣）：劣。最內層循環每處理一次，B的索引僅需+strideB，即移動到下一行，不是連續的內存訪問。
C（結果矩陣）：最優。最內層循環處理期間，C的索引保持不變。

因矩陣乘法的時間復雜度是 O(N^3)，使用立方體圖片來表示矩陣乘法的運算過程，是比較直觀的。例如下圖表示了循環次序ijk時矩陣乘法的內循環。

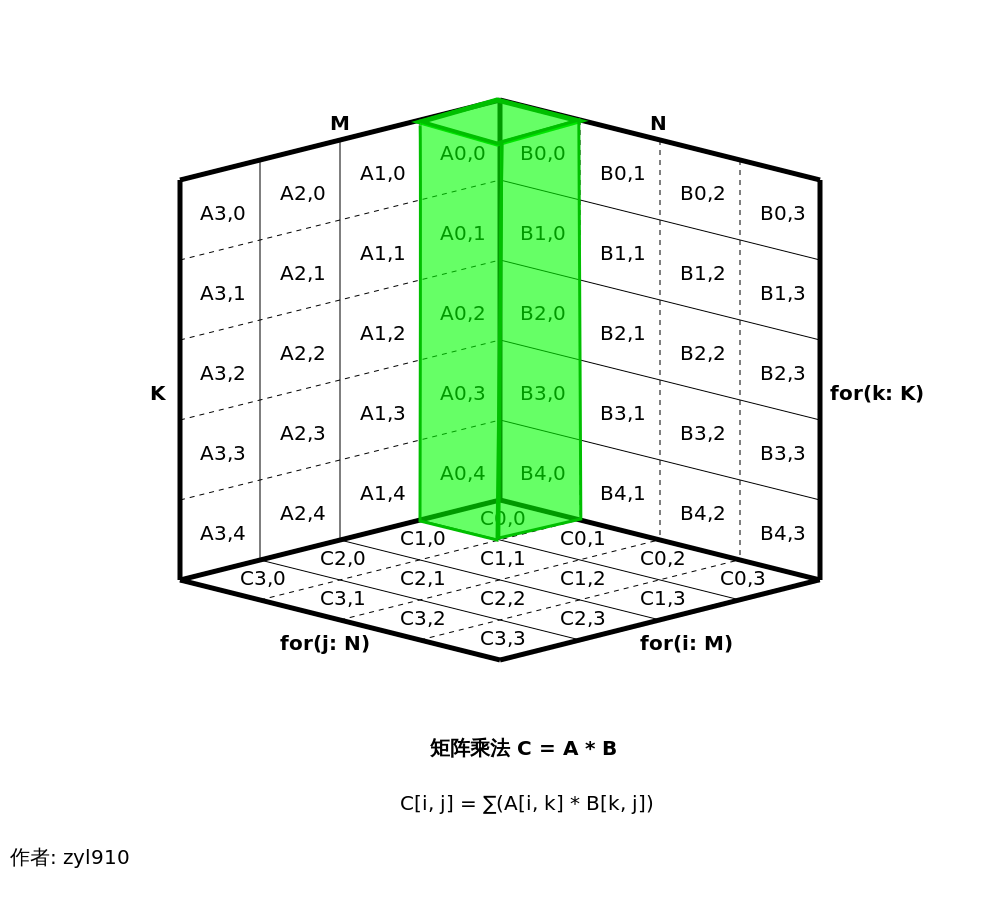
multiplymatrix4_ijk

A矩陣在左側，旋轉了90度；B矩陣在右側；C矩陣在下側。矩陣元素采取了“矩陣列號,行號”的命名風格，例如“A1,2”表示“A矩陣的第1列第2行元素”。

綠色的長方體，表示最內層循環所影響的元素。目前展示了 C[0,0] = A[0,0]*B[0,0] + A[0,1]*B[1,0] + A[0,2]*B[2,0] + A[0,3]*B[3,0] + A[0,4]*B[4,0] 的計算。這個圖中，A元素的投影與B元素的投影相交的位置，表示這2個元素值做乘法；而C元素的投影，正好覆蓋了上述相交的位置，表示對這些元素值做累加。

同一個矩陣的相鄰元素之間，虛線表示同一行的元素，實線表示同一列的元素。于是可以直觀的看到——

綠色的長方體在A矩陣上僅跨越了虛線，表示它是連續內存訪問；
而它在B矩陣上都是跨越實線，移動到下一行，這不是連續的內存訪問。

2.2.2 循環次序ikj（TileRow）

TileRow算法的循環次序是ikj，即它的最內層循環是j的循環。此時分析一下3個矩陣的數據訪問情況。

A（左矩陣）：最優。最內層循環處理期間，A的索引保持不變。
B（右矩陣）：優。最內層循環每處理一次，B的索引僅需+1，是連續的內存訪問。
C（結果矩陣）：優。最內層循環每處理一次，C的索引僅需+1，是連續的內存訪問。

我們再用立方體圖片來觀察循環次序ikj時矩陣乘法的內循環。

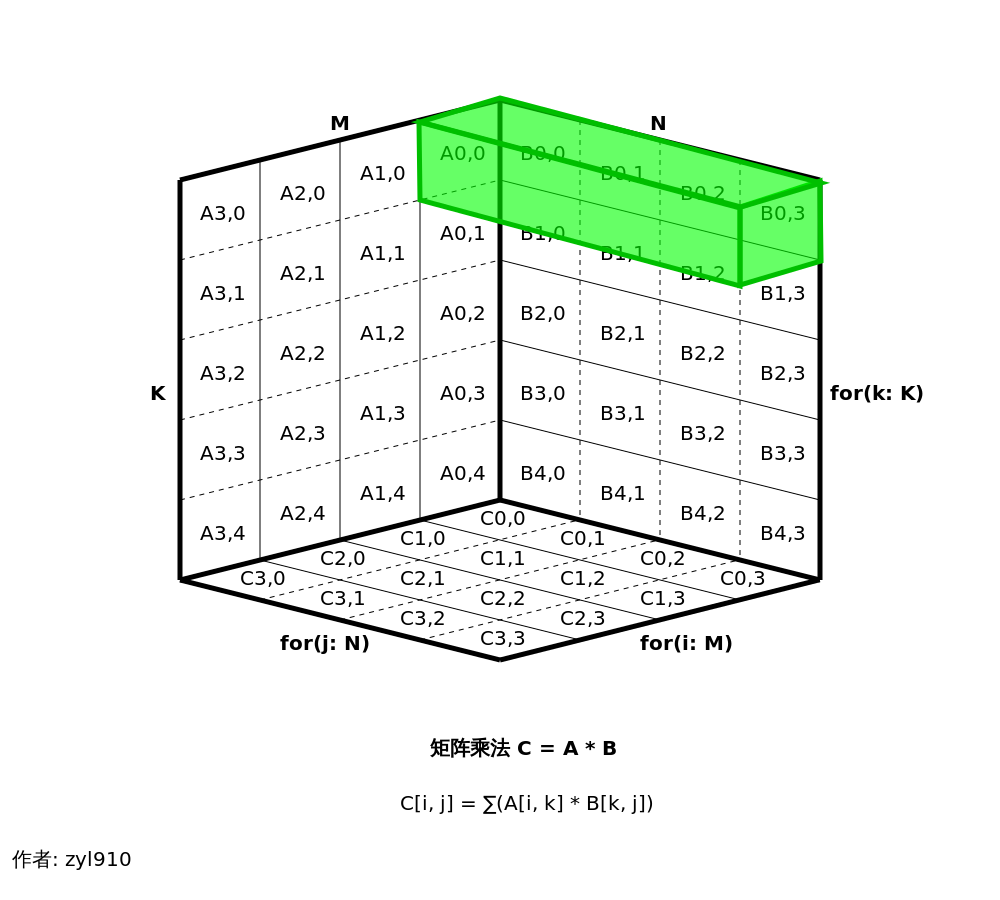
multiplymatrix4_ikj

于是可以直觀的看到——綠色的長方體在B矩陣、C矩陣上，均僅跨越了虛線，表示它們都是連續內存訪問。

對比后可以發現，ikj比ijk次序在內存訪問方面具有優勢，這就是它性能更好的原因。

2.3 使用Span及消除索引計算時的乘法開銷（TileRowSpan）

觀察上一個算法，會發現在內循環里，除了矩陣乘法運算所需的乘法，還用到2次乘法——用乘法來計算索引（bIdx、cIdx）。也就是說上一個算法至少有 3 * N^3次乘法運算，而標準矩陣乘法是 N^3次乘法運算，它多了 2倍的 N^3次乘法運算。

消除索引計算時的乘法開銷，能夠提高性能。具體辦法是根據循環的特點，在各級循環里做合適的累加操作，便能算出各索引的值。

另外，還可以用Span代替數組，使該方法不僅能支持數據等托管數據，還能支持非托管的數據。

2.3.1 算法的實現

public static void StaticTileRowSpan(int M, int N, int K, Span<TMy> A, int strideA, Span<TMy> B, int strideB, Span<TMy> C, int strideC) {
    // Clear matrix C.
    MatrixUtil.Fill((TMy)0, M, N, C, strideC);
    // Matrix multiply.
    int aIdx0 = 0;
    int cIdx0 = 0;
    for (int i = 0; i < M; ++i) {
        int aIdx = aIdx0;
        int bIdx0 = 0;
        for (int k = 0; k < K; ++k) {
            int bIdx = bIdx0;
            int cIdx = cIdx0;
            for (int j = 0; j < N; ++j) {
                C[cIdx] += A[aIdx] * B[bIdx];
                ++bIdx;
                ++cIdx;
            }
            ++aIdx;
            bIdx0 += strideB;
        }
        aIdx0 += strideA;
        cIdx0 += strideC;
    }
}

可見，現在消除了索引計算時的乘法開銷。僅在做矩陣計算時用了乘法。

2.3.2 基準測試方法

對于上面的方法，它的基準測試代碼如下。

[Benchmark]
public void TileRowSpan() {
    StaticTileRowSpan(MatrixM, MatrixN, MatrixK, arrayA!, StrideA, arrayB!, StrideB, arrayC!, StrideC);
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("TileRowSpan");
    }
}

由于Span支持數組的隱式轉換，所以基準測試方法的寫法，與上一算法相同。

2.3.3 基準測試結果

基準測試結果如下。

Method	N	Mean	Error	StdDev	Median	Ratio	RatioSD	Code Size
Basic	1024	4,712,905,103.3 ns	35,792,824.68 ns	53,573,019.05 ns	4,722,569,850.0 ns	1.000	0.02	954 B
TileRowSpan	1024	613,236,262.1 ns	6,326,567.15 ns	9,273,400.86 ns	610,494,600.0 ns	0.130	0.00	1,358 B

對測試結果進行對比——

TileRowSpan: 耗時 613,236,262.1 ns, 故 GFOPS 為 2 / 0.6132362621 ≈ 3.26, 性能是Basic的 4,712,905,103.3 / 613,236,262.1 ≈ 7.69 倍.

性能是Basic的 7.69 倍了。

2.4 使用托管指針進一步降低地址計算的開銷（TileRowRef）

上面已經消除索引計算時的乘法開銷了，但是使用索引訪問數據的本身是有一定開銷的。將索引訪問，改造為指針訪問，能進一步降低地址計算的開銷。

C/C++ 的指針，在 C# 里叫做“原生指針”（Native pointer）或“非托管指針”（Unmanaged pointer），可以在unsafe關鍵字申明的“非安全代碼”里使用，且需使用 fixed 語句鎖定數據獲取指針。

從 C# 7.3開始，可以用引用代替原生指針, 擺脫unsafe關鍵字與fixed語句，它也被稱作 “托管指針”（Managed pointer）。其編程思路與原生指針是差不多的，只是個別地方需要換一種寫法。具體辦法可參考《C# 使用SIMD向量類型加速浮點數組求和運算（4）：用引用代替指針, 擺脫unsafe關鍵字，兼談Unsafe類的使用》。

2.4.1 算法的實現

public static void StaticTileRowRef(int M, int N, int K, ref readonly TMy A, int strideA, ref readonly TMy B, int strideB, ref TMy C, int strideC) {
    // Clear matrix C.
    MatrixUtil.Fill((TMy)0, M, N, ref C, strideC);
    // Matrix multiply.
    ref TMy pA0 = ref Unsafe.AsRef(in A);
    ref TMy pC0 = ref C;
    for (int i = 0; i < M; ++i) {
        ref TMy pA = ref pA0;
        ref TMy pB0 = ref Unsafe.AsRef(in B);
        for (int k = 0; k < K; ++k) {
            TMy aValue = pA;
            ref TMy pB = ref pB0;
            ref TMy pC = ref pC0;
            for (int j = 0; j < N; ++j) {
                pC += aValue * pB;
                pB = ref Unsafe.Add(ref pB, 1);
                pC = ref Unsafe.Add(ref pC, 1);
            }
            pA = ref Unsafe.Add(ref pA, 1);
            pB0 = ref Unsafe.Add(ref pB0, strideB);
        }
        pA0 = ref Unsafe.Add(ref pA0, strideA);
        pC0 = ref Unsafe.Add(ref pC0, strideC);
    }
}

它的算法與上一算法（StaticTileRowSpan）完全相同，只是將索引計算，改為了托管指針的地址計算。

簡單說明一下，“= ref”表示托管指針地址的賦值。例如 pA = ref Unsafe.Add(ref pA, 1)，相當于原生指針的 pA += 1。雖然語法啰嗦了一些，但功能與原生指針是一樣的，且JIT編譯生成的機器碼是相同的，故性能也是相同的。

而“=”（等于符號）右邊沒有“ref”關鍵字時，這表示是普通賦值。會使用托管指針（ref）所指向的實際數據。例如 TMy aValue = pA，相當于原生指針的 TMy aValue = *pA。

Unsafe類的大部分方法僅支持“ref”，而不支持“ref readonly”。面對“ref readonly”，需使用Unsafe類的AsRef方法，對引用取消只讀（類似C++的 const_cast）。例如 ref TMy pA0 = ref Unsafe.AsRef(in A)，相當于C++指針的 TMy* pA0 = const_cast<TMy*>(A)。

2.4.1.1 矩陣清零

因現在使用了托管指針，這就沒法使用先前的Span版參數的“MatrixUtil.Fill”方法。于是新增了一個托管指針版參數的 “MatrixUtil.Fill”方法。

public static void Fill<T>(T value, nint rows, nint cols, ref T matrix, nint stride = 0) {
    if (0 == stride) {
        stride = cols;
    }
    int colsInt = (int)cols;
#if NETSTANDARD2_1_OR_GREATER || NETCOREAPP2_1_OR_GREATER
    bool useSpan = (long)cols < int.MaxValue;
#else
    bool useSpan = false;
#endif
    ref T p0 = ref matrix;
    for (nint i = 0; i < rows; i++) {
        if (useSpan) {
#if NETSTANDARD2_1_OR_GREATER || NETCOREAPP2_1_OR_GREATER
            Span<T> span = MemoryMarshal.CreateSpan(ref p0, colsInt);
            span.Fill(value);
#endif
        } else {
            ref T p = ref p0;
            for (nint j = 0; j < cols; j++) {
                p = value;
                p = ref Unsafe.Add(ref p, 1);
            }
        }
        // Next.
        p0 = ref Unsafe.Add(ref p0, stride);
    }
}

從 .NET Standard 2.1 或 .NET Core 2.1開始，能夠將托管指針轉為Span，隨后便可以利用Span的Fill方法。而對于之前的版本，需自行使用托管指針來實現功能。

Span的索引是int類型的，故它最多僅能處理 int.MaxValue (2G) 范圍內的數據。當 cols 大于該范圍時，還得使用托管指針來處理。

2.4.2 基準測試方法

對于上面的方法，它的基準測試代碼如下。

[Benchmark]
public void TileRowRef() {
    StaticTileRowRef(MatrixM, MatrixN, MatrixK, ref arrayA![0], StrideA, ref arrayB![0], StrideB, ref arrayC![0], StrideC);
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("TileRowRef");
    }
}

因StaticTileRowRef使用了托管指針，于是這里需傳遞托管指針。例如 ref arrayA![0] 表示傳遞“矩陣A首個元素的托管指針”。

2.4.3 基準測試結果

基準測試結果如下。

Method	N	Mean	Error	StdDev	Median	Ratio	RatioSD	Code Size
Basic	1024	4,712,905,103.3 ns	35,792,824.68 ns	53,573,019.05 ns	4,722,569,850.0 ns	1.000	0.02	954 B
TileRowRef	1024	332,063,973.2 ns	4,375,391.05 ns	6,275,055.62 ns	329,953,500.0 ns	0.070	0.00	1,512 B

對測試結果進行對比——

TileRowRef: 耗時 332,063,973.2 ns, 故 GFOPS 為 2 / 0.3320639732 ≈ 6.02, 性能是Basic的 4,712,905,103.3 / 332,063,973.2 ≈ 14.19 倍.

性能是Basic的 14.19 倍了。可見，即使限制在標量算法的范疇內，優化也能取得不小成果的。

三、向量算法優化與并行加速

接下來介紹 SIMD向量算法、并行加速等優化手段。

3.1 使用SIMD硬件加速技術的向量算法（TileRowSimd）

回顧一下“[2.2.2 循環次序ikj（TileRow）](#2.2.2 循環次序ikj（TileRow）)”，可以注意到——每一次內循環中，A的索引保持不變，且B、C的索引僅需+1，是連續的內存訪問。

這種情況，是能容易地改造為SIMD向量算法的。設向量寬度 W 為 Vector<TMy>.Count 的值，那么SIMD向量算法的關鍵思路如下。

“A的索引保持不變”：使用 Vector<TMy> vA = new Vector<TMy>(pA)，就能根據當前A矩陣中的元素，廣播到向量變量里（vA[i] = pA）。
“B、C的索引僅需+1”：例如使用 ref Vector<TMy> pB = ref Unsafe.As<TMy, Vector<TMy>>(ref pB0)，就能直接將 TMy 的引用，重新解釋為 Vector<TMy>的引用。繼而能夠從 pB0 這個地址開始，依次將“W個連續值”加載到向量變量里（(pB[i]) = pB0[i]）。同理可這樣加載pC。

隨后執行 pC = Vector.Add(Vector.Multiply(vA, pB), pC)，便能對這“W個連續值”中的每個元素執行 pC += vA * pB 的操作。

標量算法每次僅能處理1個值，而SIMD向量算法每次能處理 W個值，故它的理論計算性能是標量算法的 W倍。

若讀者對 .NET SIMD硬件加速技術不熟悉，可查閱 “C# 使用SIMD向量類型加速浮點數組求和運算（1）：使用Vector4、Vector<T>” 等文章。

multiplymatrix4_ikj

假設現在的向量類型是128位（如X86的SSE指令集、Arm的AdvSimd指令集），那么向量類型的字節尺寸為 128 / 8 = 16。因Single類型的尺寸是4個字節，那么向量類型里可以存儲 16 / 4 = 4個元素。即 W（Vector<TMy>.Count）的值為4，很適合處理N（B、C矩陣的列數）為4時的矩陣。例如上圖，它就是4時的矩陣，綠色長方體在標量算法時需要寫循環來實現，而用了SIMD向量算法后能一次性算出這4個值。

當N為W的整數倍時，可以多次執行上述的SIMD向量算法，使整行的數據處理完畢。若不是整數倍，則需專門處理尾部數據，下面的源代碼里使用“尾部覆蓋”的策略。

3.1.1 算法的實現

public static void StaticTileRowSimd(int M, int N, int K, ref readonly TMy A, int strideA, ref readonly TMy B, int strideB, ref TMy C, int strideC) {
    if (N < Vector<TMy>.Count || !Vector.IsHardwareAccelerated) {
        StaticTileRowRef(M, N, K, in A, strideA, in B, strideB, ref C, strideC);
        return;
    }
    int cntRem = N % Vector<TMy>.Count; // Remainder count.
    int cntBlockRaw = N / Vector<TMy>.Count; // Block count raw.
    int cntBlock = cntBlockRaw;
    if (0 == cntRem) {
        --cntBlock; // Use vCLast.
    }
    // Clear matrix C.
    MatrixUtil.Fill((TMy)0, M, N, ref C, strideC);
    // Matrix multiply.
    ref TMy pA0 = ref Unsafe.AsRef(in A);
    ref TMy pC0 = ref C;
    for (int i = 0; i < M; ++i) {
        ref TMy pA = ref pA0;
        ref TMy pB0 = ref Unsafe.AsRef(in B);
        for (int k = 0; k < K; ++k) {
            TMy aValue = pA;
            Vector<TMy> vA = new Vector<TMy>(aValue);
            // Last.
            int pos = N - Vector<TMy>.Count;
            ref Vector<TMy> pBLast = ref Unsafe.As<TMy, Vector<TMy>>(ref Unsafe.Add(ref pB0, pos));
            ref Vector<TMy> pCLast = ref Unsafe.As<TMy, Vector<TMy>>(ref Unsafe.Add(ref pC0, pos));
            Vector<TMy> vCLast = Vector.Add(Vector.Multiply(vA, pBLast), pCLast);
            // SIMD for.
            if (cntBlock >= 0) {
                ref Vector<TMy> pB = ref Unsafe.As<TMy, Vector<TMy>>(ref pB0);
                ref Vector<TMy> pC = ref Unsafe.As<TMy, Vector<TMy>>(ref pC0);
                for (int j = 0; j < cntBlock; ++j) {
                    pC = Vector.Add(Vector.Multiply(vA, pB), pC); // pC += vA * pB;
                    pB = ref Unsafe.Add(ref pB, 1);
                    pC = ref Unsafe.Add(ref pC, 1);
                }
            }
            pCLast = vCLast; // Overrride remainder items. 
            // Next.
            pA = ref Unsafe.Add(ref pA, 1);
            pB0 = ref Unsafe.Add(ref pB0, strideB);
        }
        pA0 = ref Unsafe.Add(ref pA0, strideA);
        pC0 = ref Unsafe.Add(ref pC0, strideC);
    }
}

該方法的開頭做了檢查，若發現 N < Vector<TMy>.Count（N小于向量寬度）或沒有硬件加速時，便進行回退，調用標量算法 StaticTileRowRef。

注意 pB、pC 都是 Vector<TMy> 類型的托管指針，所以在 Unsafe.Add(ref pB, 1)時，并不是對單個 TMy 元素移動指針（增加 sizeof(TMy)字節），而是對整塊 Vector<TMy> 移動指針（增加 sizeof(Vector<TMy>)字節）。

3.1.2 基準測試方法

對于上面的方法，它的基準測試代碼如下。

[Benchmark]
public void TileRowSimd() {
    StaticTileRowSimd(MatrixM, MatrixN, MatrixK, ref arrayA![0], StrideA, ref arrayB![0], StrideB, ref arrayC![0], StrideC);
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("TileRowSimd");
    }
}

3.1.3 基準測試結果

基準測試結果如下。

Method	N	Mean	Error	StdDev	Median	Ratio	RatioSD	Code Size
Basic	1024	4,712,905,103.3 ns	35,792,824.68 ns	53,573,019.05 ns	4,722,569,850.0 ns	1.000	0.02	954 B
TileRowSimd	1024	71,736,249.5 ns	2,768,453.89 ns	3,880,986.03 ns	69,775,500.0 ns	0.015	0.00	1,258 B

對測試結果進行對比——

TileRowSimd: 耗時 71,736,249.5 ns, 故 GFOPS 為 2 / 0.0717362495 ≈ 27.88, 性能是Basic的 4,712,905,103.3 / 71,736,249.5 ≈ 65.70 倍.

性能是Basic的 65.70 倍了。

3.2 基于TileRowSimd的并行加速（TileRowSimdParallel）

上面的代碼是單線程的代碼，僅能利用一個CPU核心，而現代CPU一般有多個核心。可使用并行計算，讓每一個CPU核心都分攤計算工作，從而實現了加速。

3.2.1 基準測試方法

從 .NET Framework 4.0 開始，提供了 Parallel.For 方法，用它能方便的執行并行循環。

矩陣乘法是很容易并行化的，可以將最外層的i循環，分別交給不同的線程去處理，即可看作對C（結果）矩陣每一行去做并行處理。由于TileRowSimd算法的參數定義的很靈活，于是現在調整 M的值，以及 A、C矩陣的起始位置，便能實現讓矩陣每一行去做并行處理。

所以我們不用修改TileRowSimd算法，僅需修改基準測試方法，便能增加它的并行加速的基準測試方法。

[Benchmark]
public void TileRowSimdParallel() {
    int M = MatrixM;
    bool allowParallel = (M >= 16) && (Environment.ProcessorCount > 1);
    if (allowParallel) {
        Parallel.For(0, M, i => {
            StaticTileRowSimd(1, MatrixN, MatrixK, ref arrayA![StrideA * i], StrideA, ref arrayB![0], StrideB, ref arrayC![StrideC * i], StrideC);
        });
    } else {
        StaticTileRowSimd(MatrixM, MatrixN, MatrixK, ref arrayA![0], StrideA, ref arrayB![0], StrideB, ref arrayC![0], StrideC);
    }
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("TileRowSimdParallel");
    }
}

在開始時做了一個檢查，若M的值太小，或是僅有1個處理器時，便回退為單線程算法。

3.2.2 基準測試結果

基準測試結果如下。

Method	N	Mean	Error	StdDev	Median	Ratio	RatioSD	Code Size
Basic	1024	4,712,905,103.3 ns	35,792,824.68 ns	53,573,019.05 ns	4,722,569,850.0 ns	1.000	0.02	954 B
TileRowSimdParallel	1024	11,576,096.3 ns	447,403.26 ns	669,652.19 ns	11,727,672.3 ns	0.002	0.00	8,549 B

對測試結果進行對比——

TileRowSimdParallel: 耗時 11,576,096.3 ns, 故 GFOPS 為 2 / 0.0115760963 ≈ 172.77, 性能是Basic的 4,712,905,103.3 / 11,576,096.3 ≈ 407.12 倍.

性能是Basic的 407.12 倍了。

3.3 使用FusedMultiplyAdd（TileRowSimdFmaBcl）

從 .NET 9.0 開始，向量類型增加了 FusedMultiplyAdd（融合乘加）方法。它用于計算 (left * right) + addend。它的縮寫是FMA。

現代X86及Arm處理器的向量指令集里，均支持FMA操作，可以在一條指令中完成FusedMultiplyAdd運算。它有這些優點——

速度快。在1條指令中同時計算乘法與加法。若用它來處理數據的乘法與加法，理論上是分開計算的2倍。
節省寄存器。分開計算時，需要再用一個寄存器來保存中間結果。而FMA因融合了乘法與加法，無需保存中間結果，故節省了1個寄存器。
簡化代碼。分開計算時，需要分別調用向量類型的Multiply、Add方法。而改造后，僅需調用FusedMultiplyAdd這1個方法。
精度高。通過單次舍入實現運算，相比分步計算具有更高精度。

矩陣運算中有很多乘法與加法，正好可以用上它。

3.1.1 算法的實現

#if NET9_0_OR_GREATER
public static void StaticTileRowSimdFmaBcl(int M, int N, int K, ref readonly TMy A, int strideA, ref readonly TMy B, int strideB, ref TMy C, int strideC) {
    if (N < Vector<TMy>.Count || !Vector.IsHardwareAccelerated) {
        StaticTileRowRef(M, N, K, in A, strideA, in B, strideB, ref C, strideC);
        return;
    }
    int cntRem = N % Vector<TMy>.Count; // Remainder count.
    int cntBlockRaw = N / Vector<TMy>.Count; // Block count raw.
    int cntBlock = cntBlockRaw;
    if (0 == cntRem) {
        --cntBlock; // Use vCLast.
    }
    // Clear matrix C.
    MatrixUtil.Fill((TMy)0, M, N, ref C, strideC);
    // Matrix multiply.
    ref TMy pA0 = ref Unsafe.AsRef(in A);
    ref TMy pC0 = ref C;
    for (int i = 0; i < M; ++i) {
        ref TMy pA = ref pA0;
        ref TMy pB0 = ref Unsafe.AsRef(in B);
        for (int k = 0; k < K; ++k) {
            TMy aValue = pA;
            Vector<TMy> vA = new Vector<TMy>(aValue);
            // Last.
            int pos = N - Vector<TMy>.Count;
            ref Vector<TMy> pBLast = ref Unsafe.As<TMy, Vector<TMy>>(ref Unsafe.Add(ref pB0, pos));
            ref Vector<TMy> pCLast = ref Unsafe.As<TMy, Vector<TMy>>(ref Unsafe.Add(ref pC0, pos));
            Vector<TMy> vCLast = Vector.FusedMultiplyAdd(vA, pBLast, pCLast);
            // SIMD for.
            if (cntBlock >= 0) {
                ref Vector<TMy> pB = ref Unsafe.As<TMy, Vector<TMy>>(ref pB0);
                ref Vector<TMy> pC = ref Unsafe.As<TMy, Vector<TMy>>(ref pC0);
                for (int j = 0; j < cntBlock; ++j) {
                    pC = Vector.FusedMultiplyAdd(vA, pB, pC); // pC += vA * pB;
                    pB = ref Unsafe.Add(ref pB, 1);
                    pC = ref Unsafe.Add(ref pC, 1);
                }
            }
            pCLast = vCLast; // Overrride remainder items. 
            // Next.
            pA = ref Unsafe.Add(ref pA, 1);
            pB0 = ref Unsafe.Add(ref pB0, strideB);
        }
        pA0 = ref Unsafe.Add(ref pA0, strideA);
        pC0 = ref Unsafe.Add(ref pC0, strideC);
    }
}
#endif // NET9_0_OR_GREATER

代碼改動很小，僅是將 Vector.Add(Vector.Multiply(vA, pB), pC) 改為了 Vector.FusedMultiplyAdd(vA, pB, pC)。

由于從 .NET 9.0 開始才支持 FusedMultiplyAdd，故需要使用條件編譯判斷一下 .NET 的版本。

3.1.2 基準測試方法

對于上面的方法，它的基準測試代碼如下。

#if NET9_0_OR_GREATER
[Benchmark]
public void TileRowSimdFmaBcl() {
    StaticTileRowSimdFmaBcl(MatrixM, MatrixN, MatrixK, ref arrayA![0], StrideA, ref arrayB![0], StrideB, ref arrayC![0], StrideC);
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("TileRowSimdFmaBcl");
    }
}
#endif // NET9_0_OR_GREATER

3.1.3 基準測試結果

基準測試結果如下。

Method	N	Mean	Error	StdDev	Median	Ratio	RatioSD	Code Size
Basic	1024	4,712,905,103.3 ns	35,792,824.68 ns	53,573,019.05 ns	4,722,569,850.0 ns	1.000	0.02	954 B
TileRowSimd	1024	71,736,249.5 ns	2,768,453.89 ns	3,880,986.03 ns	69,775,500.0 ns	0.015	0.00	1,258 B
TileRowSimdFmaBcl	1024	71,320,997.3 ns	1,540,394.38 ns	2,056,382.42 ns	70,551,614.3 ns	0.015	0.00	1,262 B

對測試結果進行對比——

TileRowSimd: 耗時 71,736,249.5 ns, 故 GFOPS 為 2 / 0.0717362495 ≈ 27.88, 性能是Basic的 4,712,905,103.3 / 71,736,249.5 ≈ 65.70 倍.
TileRowSimdFmaBcl: 耗時 71,320,997.3 ns, 故 GFOPS 為 2 / 0.0713209973 ≈ 28.04, 性能是Basic的 4,712,905,103.3 / 71,320,997.3 ≈ 66.08 倍.

發現一個不對勁的地方——“理論上是分開計算的2倍”，但是為什么 TileRowSimdFmaBcl 與 TileRowSimd 的性能差不多，且個別時候還更慢了？

3.1.4 加上TileRowSimdFmaX86的測試

為了確認是不是 .NET 的編譯質量問題，我又編寫了一個基準測試函數 TileRowSimdFmaX86。它直接使用 X86的 Fma.MultiplyAdd 指令，使其不再受到編譯質量的影響。源代碼如下。

#if NETCOREAPP3_0_OR_GREATER
public static void StaticTileRowSimdFmaX86(int M, int N, int K, ref readonly TMy A, int strideA, ref readonly TMy B, int strideB, ref TMy C, int strideC) {
    if (N < Vector<TMy>.Count || !Vector.IsHardwareAccelerated || !Fma.IsSupported) {
        StaticTileRowRef(M, N, K, in A, strideA, in B, strideB, ref C, strideC);
        return;
    }
    // Clear matrix C.
    MatrixUtil.Fill((TMy)0, M, N, ref C, strideC);
    // Matrix multiply.
    int cntRem = N % Vector<TMy>.Count; // Remainder count.
    int cntBlockRaw = N / Vector<TMy>.Count; // Block count raw.
    int cntBlock = cntBlockRaw;
    if (0 == cntRem) {
        --cntBlock; // Use vCLast.
    }
    ref TMy pA0 = ref Unsafe.AsRef(in A);
    ref TMy pC0 = ref C;
    for (int i = 0; i < M; ++i) {
        ref TMy pA = ref pA0;
        ref TMy pB0 = ref Unsafe.AsRef(in B);
        for (int k = 0; k < K; ++k) {
            TMy aValue = pA;
            Vector<TMy> vA = new Vector<TMy>(aValue);
            // Last.
            int pos = N - Vector<TMy>.Count;
            ref Vector<TMy> pBLast = ref Unsafe.As<TMy, Vector<TMy>>(ref Unsafe.Add(ref pB0, pos));
            ref Vector<TMy> pCLast = ref Unsafe.As<TMy, Vector<TMy>>(ref Unsafe.Add(ref pC0, pos));
            Vector<TMy> vCLast = Vector.Add(Vector.Multiply(vA, pBLast), pCLast);
            // SIMD for.
            if (cntBlock >= 0) {
                ref Vector<TMy> pB = ref Unsafe.As<TMy, Vector<TMy>>(ref pB0);
                ref Vector<TMy> pC = ref Unsafe.As<TMy, Vector<TMy>>(ref pC0);
                for (int j = 0; j < cntBlock; ++j) {
                    // pC += vA * pB;
                    if (Vector<byte>.Count == Vector256<byte>.Count) {
                        pC = Fma.MultiplyAdd(vA.AsVector256(), pB.AsVector256(), pC.AsVector256()).AsVector();
                    } else if (Vector<byte>.Count == Vector256<byte>.Count) {
                        pC = Fma.MultiplyAdd(vA.AsVector128(), pB.AsVector128(), pC.AsVector128()).AsVector();
                    } else {
                        pC = Vector.Add(Vector.Multiply(vA, pB), pC);
                    }
                    pB = ref Unsafe.Add(ref pB, 1);
                    pC = ref Unsafe.Add(ref pC, 1);
                }
            }
            pCLast = vCLast; // Overrride remainder items. 
            // Next.
            pA = ref Unsafe.Add(ref pA, 1);
            pB0 = ref Unsafe.Add(ref pB0, strideB);
        }
        pA0 = ref Unsafe.Add(ref pA0, strideA);
        pC0 = ref Unsafe.Add(ref pC0, strideC);
    }
}
#endif // NETCOREAPP3_0_OR_GREATER

3.1.4.1 TileRowSimdFmaX86的測試結果

測試之后發現 TileRowSimdFmaBcl 的性能與 TileRowSimdFmaX86 很接近。且均與 TileRowSimd 差不多。

這就表示先前并不是編譯質量問題。而是因為現在的CPU流水線調度效率已經非常高了，能夠掩蓋“乘法與加法依次計算”時的延遲，使其與FMA的性能差不多。

測試結果的稍快與稍慢，僅是測試誤差。

因耗時差不多，為了減少總測試時間，于是默認屏蔽了TileRowSimdFmaX86的基準測試。有興趣的讀者可以自行嘗試。

3.4 將乘加運算封裝為函數且測試并行加速（TileRowSimdFma、TileRowSimdFmaParallel）

雖然 FusedMultiplyAdd 很好用，能簡化矩陣乘法的代碼。可它需要 .NET 9.0 或更高版本，早期版本的 .NET 用不了它。

于是可以將乘加運算封裝為函數， .NET 9.0使用FusedMultiplyAdd，早期的 .NET 便回退為乘法與加法。這樣便能在矩陣運算法時放心的使用該函數了。

且對它進行并行加速的基準測試，檢查它會不會拖慢性能。

3.4.1 乘加運算封裝為函數

由于回退為分開計算乘法與及加法，不再是融合（Fused）計算。故這個函數命名為“MultiplyAdd”比較好。

建立 VectorHelper 類，增加“MultiplyAdd”方法。

[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static Vector<float> MultiplyAdd(Vector<float> left, Vector<float> right, Vector<float> addend) {
#if NET9_0_OR_GREATER
    return Vector.FusedMultiplyAdd(left, right, addend);
#else
    return Vector.Add(addend, Vector.Multiply(left, right));
#endif // NET9_0_OR_GREATER
}

該函數設置了MethodImpl特性，并傳遞了 MethodImplOptions.AggressiveInlining 標識，使該函數能盡可能地內聯。這能避免調用函數的開銷與內存傳值的開銷。

3.4.2 矩陣乘法的代碼

使用 VectorHelper.MultiplyAdd，能像FusedMultiplyAdd一樣簡化矩陣乘法的代碼。

public static void StaticTileRowSimdFma(int M, int N, int K, ref readonly TMy A, int strideA, ref readonly TMy B, int strideB, ref TMy C, int strideC) {
    if (N < Vector<TMy>.Count || !Vector.IsHardwareAccelerated) {
        StaticTileRowRef(M, N, K, in A, strideA, in B, strideB, ref C, strideC);
        return;
    }
    int cntRem = N % Vector<TMy>.Count; // Remainder count.
    int cntBlockRaw = N / Vector<TMy>.Count; // Block count raw.
    int cntBlock = cntBlockRaw;
    if (0 == cntRem) {
        --cntBlock; // Use vCLast.
    }
    // Clear matrix C.
    MatrixUtil.Fill((TMy)0, M, N, ref C, strideC);
    // Matrix multiply.
    ref TMy pA0 = ref Unsafe.AsRef(in A);
    ref TMy pC0 = ref C;
    for (int i = 0; i < M; ++i) {
        ref TMy pA = ref pA0;
        ref TMy pB0 = ref Unsafe.AsRef(in B);
        for (int k = 0; k < K; ++k) {
            TMy aValue = pA;
            Vector<TMy> vA = new Vector<TMy>(aValue);
            // Last.
            int pos = N - Vector<TMy>.Count;
            ref Vector<TMy> pBLast = ref Unsafe.As<TMy, Vector<TMy>>(ref Unsafe.Add(ref pB0, pos));
            ref Vector<TMy> pCLast = ref Unsafe.As<TMy, Vector<TMy>>(ref Unsafe.Add(ref pC0, pos));
            //Vector<TMy> vCLast = Vector.FusedMultiplyAdd(vA, pBLast, pCLast);
            Vector<TMy> vCLast = VectorHelper.MultiplyAdd(vA, pBLast, pCLast);
            // SIMD for.
            if (cntBlock >= 0) {
                ref Vector<TMy> pB = ref Unsafe.As<TMy, Vector<TMy>>(ref pB0);
                ref Vector<TMy> pC = ref Unsafe.As<TMy, Vector<TMy>>(ref pC0);
                for (int j = 0; j < cntBlock; ++j) {
                    //pC = Vector.FusedMultiplyAdd(vA, pB, pC); // pC += vA * pB;
                    pC = VectorHelper.MultiplyAdd(vA, pB, pC); // pC += vA * pB;
                    pB = ref Unsafe.Add(ref pB, 1);
                    pC = ref Unsafe.Add(ref pC, 1);
                }
            }
            pCLast = vCLast; // Overrride remainder items. 
            // Next.
            pA = ref Unsafe.Add(ref pA, 1);
            pB0 = ref Unsafe.Add(ref pB0, strideB);
        }
        pA0 = ref Unsafe.Add(ref pA0, strideA);
        pC0 = ref Unsafe.Add(ref pC0, strideC);
    }
}

3.4.3 基準測試方法

對于上面的方法，它的基準測試代碼如下。

[Benchmark]
public void TileRowSimdFma() {
    StaticTileRowSimdFma(MatrixM, MatrixN, MatrixK, ref arrayA![0], StrideA, ref arrayB![0], StrideB, ref arrayC![0], StrideC);
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("TileRowSimdFma");
    }
}

public void TileRowSimdFmaParallel() {
    int M = MatrixM;
    bool allowParallel = (M >= 16) && (Environment.ProcessorCount > 1);
    if (allowParallel) {
        Parallel.For(0, M, i => {
            StaticTileRowSimdFma(1, MatrixN, MatrixK, ref arrayA![StrideA * i], StrideA, ref arrayB![0], StrideB, ref arrayC![StrideC * i], StrideC);
        });
    } else {
        StaticTileRowSimdFma(MatrixM, MatrixN, MatrixK, ref arrayA![0], StrideA, ref arrayB![0], StrideB, ref arrayC![0], StrideC);
    }
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("TileRowSimdParallel");
    }
}

上面同時給出了單線程與并行版的基準測試代碼。

3.4.4 基準測試結果

基準測試結果如下。

Method	N	Mean	Error	StdDev	Median	Ratio	RatioSD	Code Size
Basic	1024	4,712,905,103.3 ns	35,792,824.68 ns	53,573,019.05 ns	4,722,569,850.0 ns	1.000	0.02	954 B
TileRowSimd	1024	71,736,249.5 ns	2,768,453.89 ns	3,880,986.03 ns	69,775,500.0 ns	0.015	0.00	1,258 B
TileRowSimdFmaBcl	1024	71,320,997.3 ns	1,540,394.38 ns	2,056,382.42 ns	70,551,614.3 ns	0.015	0.00	1,262 B
TileRowSimdFma	1024	72,957,369.2 ns	3,088,652.97 ns	4,329,860.46 ns	71,072,300.0 ns	0.015	0.00	1,262 B
TileRowSimdParallel	1024	11,576,096.3 ns	447,403.26 ns	669,652.19 ns	11,727,672.3 ns	0.002	0.00	8,549 B
TileRowSimdFmaParallel	1024	12,234,503.5 ns	337,579.48 ns	505,273.12 ns	12,306,358.6 ns	0.003	0.00	8,565 B

對測試結果進行對比——

TileRowSimd: 耗時 71,736,249.5 ns, 故 GFOPS 為 2 / 0.0717362495 ≈ 27.88, 性能是Basic的 4,712,905,103.3 / 71,736,249.5 ≈ 65.70 倍.
TileRowSimdFmaBcl: 耗時 71,320,997.3 ns, 故 GFOPS 為 2 / 0.0713209973 ≈ 28.04, 性能是Basic的 4,712,905,103.3 / 71,320,997.3 ≈ 66.08 倍.
TileRowSimdFma: 耗時 72,957,369.2 ns, 故 GFOPS 為 2 / 0.0729573692 ≈ 27.41, 性能是Basic的 4,712,905,103.3 / 72,957,369.2 ≈ 64.60 倍.
TileRowSimdParallel: 耗時 11,576,096.3 ns, 故 GFOPS 為 2 / 0.0115760963 ≈ 172.77, 性能是Basic的 4,712,905,103.3 / 11,576,096.3 ≈ 407.12 倍.
TileRowSimdFmaParallel: 耗時 12,234,503.5 ns, 故 GFOPS 為 2 / 0.0122345035 ≈ 163.47, 性能是Basic的 4,712,905,103.3 / 12,234,503.5 ≈ 385.21 倍.

2種Parallel算法的耗時差不多，且3種單線程算法的耗時也差不多，都在誤差范圍內。看來 VectorHelper.MultiplyAdd 與手動使用 FusedMultiplyAdd 的性能差不多。考慮到它具有簡化代碼等優點，故值得使用。

四、矩陣分塊優化

要想進一步提高矩陣乘法的性能，需要對矩形進行分塊（Block）。對矩形進行分塊后，能利用緩存局部性減少內存訪問次數，從而提高的了性能。

首先分塊策略有許多種，且同一種分塊策略對于不同的矩陣尺寸，效果是不一樣的。即使是同一種分塊策略、同一種矩陣尺寸，也會因為CPU微架構、高速緩存尺寸等情況的不同，而表現不同，甚至還有性能下降的。

需要經過大量測試，才能找到各個處理器的最佳分塊策略。

4.1 4行、1倍向量寬度、ijk順序的分塊算法（`BlockM4Nv1_ijk_M32`、`BlockM4Nv1_ijk_M32Parallel`）

首先回顧一下 [3.1 使用SIMD硬件加速技術的向量算法（TileRowSimd）](#3.1 使用SIMD硬件加速技術的向量算法（TileRowSimd）)

multiplymatrix4_ikj

設向量寬度 W 為 Vector<TMy>.Count 的值，此時向量算法內循環是處理了 1行、W個列的數據。

若向量算法不再僅處理1行數據，而是處理4行數據，便能進一步提高性能。將它稱作“4行、1倍向量寬度”算法。

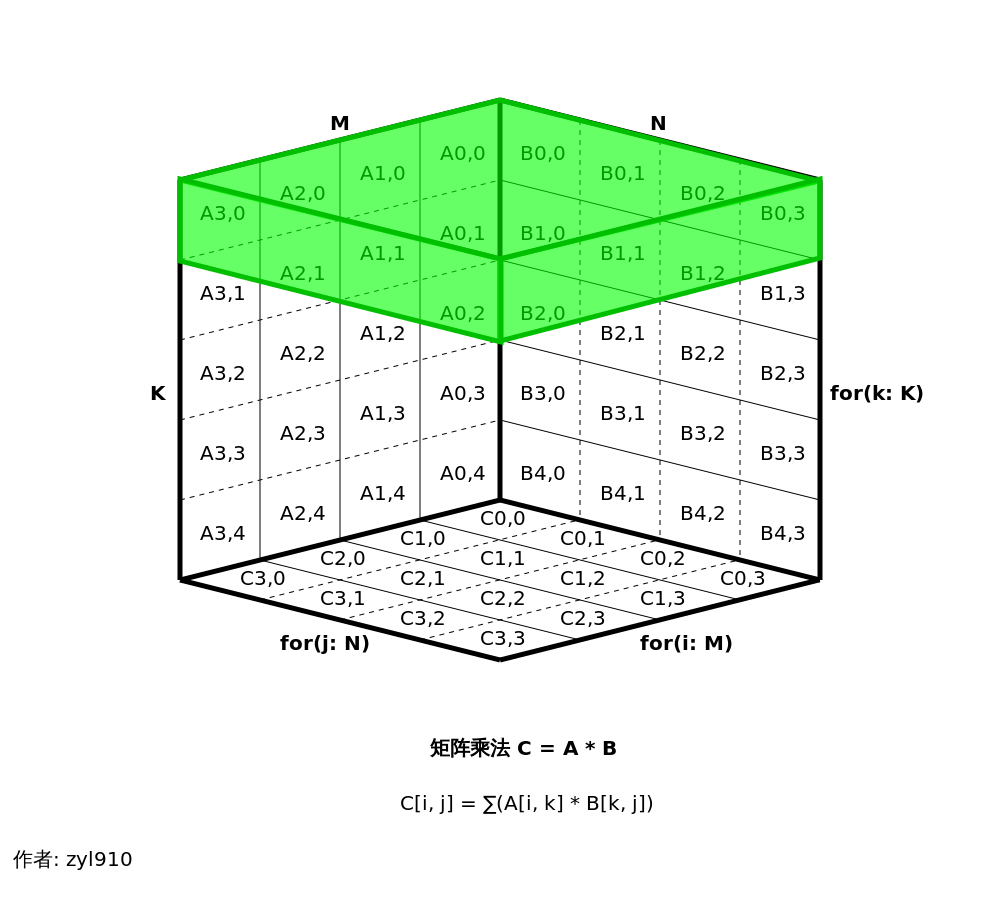
multiplymatrix4_m4n4

上面的立方圖圖片展示了 M、N都是4時的矩陣，且采用的是128位向量，使W的值為4。于是，一筆“4行、1倍向量寬度”數據正好完成了水平方向1整層數據處理，隨后圖中的垂直方向（K的方向）循環對每一層結果的累加操作，便能算出完整的矩陣乘法結果。這種算法被稱作“外積累加”算法，其中水平方向1整層的運算是向量的“外積”運算。該算法也被稱作“kij”或“K-M-N”算法，因最外層是K循環，隨后水平方向1整層的運算可看作“M循環嵌套N循環”。

若直接對大矩陣按“kij”的順序做矩陣乘法的運算，需要頻繁讀寫C矩陣的元素，導致性能很差。但對于“4行、1倍向量寬度”的算法來說，結果矩陣C正好可以用4個向量寄存器來存儲。于是在k循環過程中，完全不需要對C矩陣進行讀寫，全是高效向量寄存器運算操作。直到循環處理完成后，才將向量寄存器中的數據保存到C矩陣，這便大大減少了內存訪問的開銷。

“4行、1倍向量寬度”算法的內循環在行、列這2個方向上都是處理多個數據，導致經典的3層循環將難以處理完整矩陣乘法。此時可將內循環看作“4行、1倍向量寬度”的子矩陣，然后利用矩陣分塊的策略來處理數據。

由于此時矩陣乘法的完整算法比較復雜，故拆分為3個部分來處理比較好——公共方法、內核算法、完整算法。

4.1.1 公共方法的改進

從 .NET 8.0 開始，Vector靜態類增加了 LoadUnsafe、StoreUnsafe 方法，能便于向量類型的加載。

本程序為了對比測試各個 .NET 版本，于是需要對這些方法進行兼容處理。于是在 VectorHelper 類中增加了這些函數

#if NET8_0_OR_GREATER
#else
#define VECTOR_WHERE_STRUCT// Since .NET8, Vector type not have `where T : struct`.
#endif // NET8_0_OR_GREATER

[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static Vector<T> LoadUnsafe<T>(ref readonly T source)
#if VECTOR_WHERE_STRUCT
        where T : struct
#endif // VECTOR_WHERE_STRUCT
        {
#if NET8_0_OR_GREATER
    return Vector.LoadUnsafe(in source);
#else
    return Unsafe.As<T, Vector<T>>(ref Unsafe.AsRef(in source));
#endif // NET8_0_OR_GREATER
}

[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static void StoreUnsafe<T>(
#if !NET8_0_OR_GREATER
    this
#endif // NET8_0_OR_GREATER
    Vector<T> source, ref T destination)
#if VECTOR_WHERE_STRUCT
        where T : struct
#endif // VECTOR_WHERE_STRUCT
        {
#if NET8_0_OR_GREATER
    Vector.StoreUnsafe(source, ref destination);
#else
    Unsafe.As<T, Vector<T>>(ref destination) = source;
#endif // NET8_0_OR_GREATER
}

從 .NET 8.0 開始，向量類型取消了 struct 的約束。于是本類也遵從了這個規則。

4.1.2 矩陣乘法內核算法

將矩陣進行分塊后，對于每個分塊，專門用一個方法來處比較好。這種方法，不再時處理整個矩陣，而僅是單個分塊，故一般稱它為內核算法。

內核算法不用管理矩陣的清零操作，且一般僅需支持固定尺寸的數據。

為了便于測試各種矩陣分塊策略，我這邊會傳遞固定尺寸的整數倍的數據。于是m、n、k這3個參數也需做循環處理，只是不用考慮非整數倍數據。

private static void GemmKernelM4Nv1(int M, int N, int K, ref readonly TMy A, int strideA, ref readonly TMy B, int strideB, ref TMy C, int strideC) {
    const int blockM = 4;
    int vectorWidth = Vector<TMy>.Count;
    int blockN = vectorWidth * 1;
    if (0 != (M % blockM)) {
        throw new ArgumentException(string.Format("The M({0}) of block is not an integer multiple of {1}!", M, blockM));
    }
    if (0 != (N % blockN)) {
        throw new ArgumentException(string.Format("The N({0}) of block is not an integer multiple of {1}!", N, blockN));
    }
    // Matrix multiply.
    ref TMy pA0 = ref Unsafe.AsRef(in A);
    ref TMy pB0 = ref Unsafe.AsRef(in B);
    ref TMy pC0 = ref C;
    for (int i = 0; i < M; i += blockM) {
        ref TMy pCLine = ref pC0;
        for (int j = 0; j < N; j += blockN) {
            ref TMy pC = ref pCLine;
            Vector<TMy> c0;
            Vector<TMy> c1;
            Vector<TMy> c2;
            Vector<TMy> c3;
            c0 = VectorHelper.LoadUnsafe(ref pC); pC = ref Unsafe.Add(ref pC, strideC);
            c1 = VectorHelper.LoadUnsafe(ref pC); pC = ref Unsafe.Add(ref pC, strideC);
            c2 = VectorHelper.LoadUnsafe(ref pC); pC = ref Unsafe.Add(ref pC, strideC);
            c3 = VectorHelper.LoadUnsafe(ref pC);
            // Add.
            ref TMy pALine = ref pA0;
            ref TMy pB = ref Unsafe.Add(ref pB0, j);
            for (int k = 0; k < K; ++k) {
                // pC += pA * pB;
                Vector<TMy> b = VectorHelper.LoadUnsafe(ref pB);
                ref TMy pA = ref pALine;
                c0 = VectorHelper.MultiplyAdd(new Vector<TMy>(pA), b, c0); pA = ref Unsafe.Add(ref pA, strideA);
                c1 = VectorHelper.MultiplyAdd(new Vector<TMy>(pA), b, c1); pA = ref Unsafe.Add(ref pA, strideA);
                c2 = VectorHelper.MultiplyAdd(new Vector<TMy>(pA), b, c2); pA = ref Unsafe.Add(ref pA, strideA);
                c3 = VectorHelper.MultiplyAdd(new Vector<TMy>(pA), b, c3);
                // Next.
                pALine = ref Unsafe.Add(ref pALine, 1);
                pB = ref Unsafe.Add(ref pB, strideB);
            }
            // Store.
            pC = ref pCLine;
            VectorHelper.StoreUnsafe(c0, ref pC); pC = ref Unsafe.Add(ref pC, strideC);
            VectorHelper.StoreUnsafe(c1, ref pC); pC = ref Unsafe.Add(ref pC, strideC);
            VectorHelper.StoreUnsafe(c2, ref pC); pC = ref Unsafe.Add(ref pC, strideC);
            VectorHelper.StoreUnsafe(c3, ref pC);
            // Next.
            pCLine = ref Unsafe.Add(ref pCLine, blockN);
        }
        pA0 = ref Unsafe.Add(ref pA0, strideA * blockM);
        pC0 = ref Unsafe.Add(ref pC0, strideC * blockM);
    }
}

4.1.3 矩陣乘法完整算法

為了便于測試各種分塊尺寸，完整算法增加了 blockM、blockN、blockK 參數。且為了便于并行計算，增加了 allowParallel 參數。

internal unsafe static void StaticBlockM4Nv1_ijk(int M, int N, int K, ref readonly TMy A, int strideA, ref readonly TMy B, int strideB, ref TMy C, int strideC, int blockM, int blockN, int blockK, bool allowParallel = false) {
    if (0 != (M % blockM)) {
        throw new ArgumentException(string.Format("The M({0}) is not an integer multiple of {1}!", M, blockM));
    }
    if (0 != (N % blockN)) {
        throw new ArgumentException(string.Format("The N({0}) is not an integer multiple of {1}!", N, blockN));
    }
    if (0 != (K % blockK)) {
        throw new ArgumentException(string.Format("The K({0}) is not an integer multiple of {1}!", K, blockK));
    }
    // Clear matrix C.
    MatrixUtil.Fill((TMy)0, M, N, ref C, strideC);
    // Body.
    int strideB_blockK = strideB * blockK;
    ref TMy pA0 = ref Unsafe.AsRef(in A);
    ref TMy pB0 = ref Unsafe.AsRef(in B);
    if (allowParallel) {
        fixed (TMy* pA = &pA0, pB = &pB0, pC = &C) {
            nint addressA = (nint)pA;
            nint addressB = (nint)pB;
            nint addressC = (nint)pC;
            int cnt = M / blockM;
            Parallel.For(0, cnt, idx => {
                int i = idx * blockM;
                ref TMy refA = ref Unsafe.AsRef<TMy>((void*)addressA);
                ref TMy refB = ref Unsafe.AsRef<TMy>((void*)addressB);
                ref TMy refC = ref Unsafe.AsRef<TMy>((void*)addressC);
                RunByI(M, N, K, ref refA, strideA, ref refB, strideB, ref refC, strideC, i);
            });
        }
    } else {
        for (int i = 0; i < M; i += blockM) {
            RunByI(M, N, K, ref pA0, strideA, ref pB0, strideB, ref C, strideC, i);
        }
    }

    void RunByI(int M, int N, int K, ref TMy A, int strideA, ref TMy B, int strideB, ref TMy C, int strideC, int i) {
        ref TMy pA0 = ref Unsafe.Add(ref A, strideA * i);
        ref TMy pCLine = ref Unsafe.Add(ref C, strideC * i);
        for (int j = 0; j < N; j += blockN) {
            ref TMy pALine = ref pA0;
            ref TMy pB = ref Unsafe.Add(ref B, j);
            for (int k = 0; k < K; k += blockK) {
                GemmKernelM4Nv1(blockM, blockN, blockK, in pALine, strideA, in pB, strideB, ref pCLine, strideC);
                // Next.
                pALine = ref Unsafe.Add(ref pALine, blockK);
                pB = ref Unsafe.Add(ref pB, strideB_blockK);
            }
            // Next.
            pCLine = ref Unsafe.Add(ref pCLine, blockN);
        }
    }
}

internal static void StaticBlockM4Nv1_ijk_M32(int M, int N, int K, ref readonly TMy A, int strideA, ref readonly TMy B, int strideB, ref TMy C, int strideC, bool allowParallel = false) {
    StaticBlockM4Nv1_ijk(M, N, K, in A, strideA, in B, strideB, ref C, strideC, 32, 32, 32, allowParallel);
}

由于并行算法比較復雜，可以先看單線程的算法，即 allowParallel 為 false的分支。它先使用變量i對M進行循環處理，步長為blockM，逐個調用了 RunByI 方法。RunByI 是一個本地方法，它用了2層循環分別在 N、K方向處理數據，將每一個分塊交給GemmKernelM4Nv1去處理。

隨后再來看并行版算法，即 allowParallel 為 true的分支。它的原理并不復雜，就是使用 Parallel.For 并發的處理數據。但是為了避免 C# 安全檢測“托管指針或原生指針都不能跨越異步方法的邊界”報錯，加了一些繁瑣的轉換，解決了指針傳遞問題。

使用 fixed語句，鎖定數據獲取原生指針（如 pA）。
使用強制類型轉換，將原生指針轉為nint（如 addressA）。
在匿名方法內，使用強制類型轉換，將nint轉為原生指針（如 (void*)addressA）。
最后使用 Unsafe.AsRef，將原生指針轉為托管指針（如 refA）。從而能夠調用 RunByI 等方法了。

這些步驟用 C# 寫起來是比較繁瑣的，但這些不同類型的變量其實是同一個值，運行起來的實際開銷很低。

并增加了 StaticBlockM4Nv1_ijk_M32 方法，專門對 32*32*32 的分塊尺寸進行基準測試。

4.1.4 基準測試方法

對于上面的方法，它的基準測試代碼如下。

[Benchmark]
public void BlockM4Nv1_ijk_M32() {
    StaticBlockM4Nv1_ijk_M32(MatrixM, MatrixN, MatrixK, ref arrayA![0], StrideA, ref arrayB![0], StrideB, ref arrayC![0], StrideC);
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("BlockM4Nv1_ijk_M32");
    }
}

[Benchmark]
public void BlockM4Nv1_ijk_M32Parallel() {
    StaticBlockM4Nv1_ijk_M32(MatrixM, MatrixN, MatrixK, ref arrayA![0], StrideA, ref arrayB![0], StrideB, ref arrayC![0], StrideC, true);
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("BlockM4Nv1_ijk_M32Parallel");
    }
}

這次寫了2個基準測試方法，分別是單線程與并行計算的。由于 StaticBlockM4Nv1_ijk_M32 提供了allowParallel參數，于是基準測試方法寫起來比較簡單，僅需處理好 allowParallel 參數的傳遞。

4.1.5 基準測試結果

基準測試結果如下。

Method	N	Mean	Error	StdDev	Median	Ratio	RatioSD	Code Size
Basic	1024	4,712,905,103.3 ns	35,792,824.68 ns	53,573,019.05 ns	4,722,569,850.0 ns	1.000	0.02	954 B
BlockM4Nv1_ijk_M32	1024	155,479,981.2 ns	925,593.09 ns	1,327,458.06 ns	155,197,087.5 ns	0.033	0.00	NA
BlockM4Nv1_ijk_M32Parallel	1024	18,389,778.0 ns	391,156.50 ns	573,352.18 ns	18,200,718.8 ns	0.004	0.00	NA

對測試結果進行對比——

BlockM4Nv1_ijk_M32: 耗時 155,479,981.2 ns, 故 GFOPS 為 2 / 0.1554799812 ≈ 12.86, 性能是Basic的 4,712,905,103.3 / 155,479,981.2 ≈ 30.31 倍.
BlockM4Nv1_ijk_M32Parallel: 耗時 18,389,778.0 ns, 故 GFOPS 為 2 / 0.0183897780 ≈ 108.76, 性能是Basic的 4,712,905,103.3 / 18,389,778.0 ≈ 256.28 倍.

雖然這些算法也是比較快的，但它未能突破未分塊TileRowSimdParallel算法407.12倍的記錄。這個一方面是分塊策略的影響，另一方面與CPU微架構、高速緩存大小等因素有關。在一些Intel的CPU上測試過，BlockM4Nv1_ijk_M32Parallel與TileRowSimdParallel的性能差不多的，且矩陣越大時BlockM4Nv1_ijk_M32Parallel的領先程度更大。

4.2 4行、1倍向量寬度、ikj順序的分塊算法（`BlockM4Nv1_ikj_M32`、`BlockM4Nv1_ikj_M32Parallel`、`BlockM4Nv1_ikj_M4`、`BlockM4Nv1_ikj_M4Parallel`）

上面算法在進行分塊時，用的是 ijk順序。而ikj順序的對連續內存訪問更加友好，于是可以測試一下。

4.2.1 矩陣乘法內核算法

矩陣乘法內核算法不用修改，仍然沿用。

4.2.2 矩陣乘法完整算法

將 ijk 順序，改為 ikj 順序。

public const int CommonBlockK = 32;

internal unsafe static void StaticBlockM4Nv1_ikj(int M, int N, int K, ref readonly TMy A, int strideA, ref readonly TMy B, int strideB, ref TMy C, int strideC, int blockM, int blockN, int blockK, bool allowParallel = false) {
    if (0 != (M % blockM)) {
        throw new ArgumentException(string.Format("The M({0}) is not an integer multiple of {1}!", M, blockM));
    }
    if (0 != (N % blockN)) {
        throw new ArgumentException(string.Format("The N({0}) is not an integer multiple of {1}!", N, blockN));
    }
    if (0 != (K % blockK)) {
        throw new ArgumentException(string.Format("The K({0}) is not an integer multiple of {1}!", K, blockK));
    }
    // Clear matrix C.
    MatrixUtil.Fill((TMy)0, M, N, ref C, strideC);
    // Body.
    int strideB_blockK = strideB * blockK;
    ref TMy pA0 = ref Unsafe.AsRef(in A);
    ref TMy pB0 = ref Unsafe.AsRef(in B);
    if (allowParallel) {
        fixed (TMy* pA = &pA0, pB = &pB0, pC = &C) {
            nint addressA = (nint)pA;
            nint addressB = (nint)pB;
            nint addressC = (nint)pC;
            int cnt = M / blockM;
            Parallel.For(0, cnt, idx => {
                int i = idx * blockM;
                ref TMy refA = ref Unsafe.AsRef<TMy>((void*)addressA);
                ref TMy refB = ref Unsafe.AsRef<TMy>((void*)addressB);
                ref TMy refC = ref Unsafe.AsRef<TMy>((void*)addressC);
                RunByI(M, N, K, ref refA, strideA, ref refB, strideB, ref refC, strideC, i);
            });
        }
    } else {
        for (int i = 0; i < M; i += blockM) {
            RunByI(M, N, K, ref pA0, strideA, ref pB0, strideB, ref C, strideC, i);
        }
    }

    void RunByI(int M, int N, int K, ref TMy A, int strideA, ref TMy B, int strideB, ref TMy C, int strideC, int i) {
        ref TMy pALine = ref Unsafe.Add(ref A, strideA * i);
        ref TMy pCLine = ref Unsafe.Add(ref C, strideC * i);
        ref TMy pBLine = ref B;
        for (int k = 0; k < K; k += blockK) {
            ref TMy pB = ref pBLine;
            ref TMy pC = ref pCLine;
            for (int j = 0; j < N; j += blockN) {
                GemmKernelM4Nv1(blockM, blockN, blockK, in pALine, strideA, in pB, strideB, ref pC, strideC);
                // Next.
                pB = ref Unsafe.Add(ref pB, blockN);
                pC = ref Unsafe.Add(ref pC, blockN);
            }
            // Next.
            pALine = ref Unsafe.Add(ref pALine, blockK);
            pBLine = ref Unsafe.Add(ref pBLine, strideB_blockK);
        }
    }
}

internal static void StaticBlockM4Nv1_ikj_M32(int M, int N, int K, ref readonly TMy A, int strideA, ref readonly TMy B, int strideB, ref TMy C, int strideC, bool allowParallel = false) {
    //int blockN = 32;
    int blockN = Vector<TMy>.Count * 16;
    if (blockN > N) {
        blockN = N;
    }
    StaticBlockM4Nv1_ikj(M, N, K, in A, strideA, in B, strideB, ref C, strideC, 32, blockN, CommonBlockK, allowParallel);
}

internal static void StaticBlockM4Nv1_ikj_M4(int M, int N, int K, ref readonly TMy A, int strideA, ref readonly TMy B, int strideB, ref TMy C, int strideC, bool allowParallel = false) {
    //int blockN = 32;
    int blockN = Vector<TMy>.Count * 16;
    if (blockN > N) {
        blockN = N;
    }
    StaticBlockM4Nv1_ikj(M, N, K, in A, strideA, in B, strideB, ref C, strideC, 4, blockN, CommonBlockK, allowParallel);
}

這次提供了2種分塊策略——

M4：M為4，N為16倍向量寬度。
M32：M為32，N為16倍向量寬度。

4.2.3 基準測試方法

對于上面的方法，它的基準測試代碼如下。

[Benchmark]
public void BlockM4Nv1_ikj_M32() {
    StaticBlockM4Nv1_ikj_M32(MatrixM, MatrixN, MatrixK, ref arrayA![0], StrideA, ref arrayB![0], StrideB, ref arrayC![0], StrideC);
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("BlockM4Nv1_ikj_M32");
    }
}

[Benchmark]
public void BlockM4Nv1_ikj_M32Parallel() {
    StaticBlockM4Nv1_ikj_M32(MatrixM, MatrixN, MatrixK, ref arrayA![0], StrideA, ref arrayB![0], StrideB, ref arrayC![0], StrideC, true);
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("BlockM4Nv1_ikj_M32Parallel");
    }
}

[Benchmark]
public void BlockM4Nv1_ikj_M4() {
    StaticBlockM4Nv1_ikj_M4(MatrixM, MatrixN, MatrixK, ref arrayA![0], StrideA, ref arrayB![0], StrideB, ref arrayC![0], StrideC);
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("BlockM4Nv1_ikj_M4");
    }
}

[Benchmark]
public void BlockM4Nv1_ikj_M4Parallel() {
    StaticBlockM4Nv1_ikj_M4(MatrixM, MatrixN, MatrixK, ref arrayA![0], StrideA, ref arrayB![0], StrideB, ref arrayC![0], StrideC, true);
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("BlockM4Nv1_ikj_M4Parallel");
    }
}

4.2.4 基準測試結果

基準測試結果如下。

Method	N	Mean	Error	StdDev	Median	Ratio	RatioSD	Code Size
Basic	1024	4,712,905,103.3 ns	35,792,824.68 ns	53,573,019.05 ns	4,722,569,850.0 ns	1.000	0.02	954 B
BlockM4Nv1_ikj_M32	1024	158,203,231.7 ns	1,098,377.31 ns	1,643,999.58 ns	157,511,900.0 ns	0.034	0.00	2,303 B
BlockM4Nv1_ikj_M32Parallel	1024	15,417,779.4 ns	528,972.18 ns	775,360.62 ns	15,101,640.6 ns	0.003	0.00	9,453 B
BlockM4Nv1_ikj_M4	1024	159,175,464.8 ns	2,913,579.61 ns	4,084,432.04 ns	161,698,000.0 ns	0.034	0.00	2,188 B
BlockM4Nv1_ikj_M4Parallel	1024	17,944,453.9 ns	584,658.22 ns	856,984.51 ns	17,830,587.5 ns	0.004	0.00	9,311 B

對測試結果進行對比——

BlockM4Nv1_ikj_M32: 耗時 158,203,231.7 ns, 故 GFOPS 為 2 / 0.1582032317 ≈ 12.64, 性能是Basic的 4,712,905,103.3 / 158,203,231.7 ≈ 29.79 倍.
BlockM4Nv1_ikj_M32Parallel: 耗時 15,417,779.4 ns, 故 GFOPS 為 2 / 0.0154177794 ≈ 129.72, 性能是Basic的 4,712,905,103.3 / 15,417,779.4 ≈ 305.68 倍.
BlockM4Nv1_ikj_M4: 耗時 159,175,464.8 ns, 故 GFOPS 為 2 / 0.1591754648 ≈ 12.56, 性能是Basic的 4,712,905,103.3 / 159,175,464.8 ≈ 29.61 倍.
BlockM4Nv1_ikj_M4Parallel: 耗時 17,944,453.9 ns, 故 GFOPS 為 2 / 0.0179444539 ≈ 111.46, 性能是Basic的 4,712,905,103.3 / 17,944,453.9 ≈ 262.64 倍.

比起 ijk順序，ikj順序要稍微快一些，尤其是在并行運算時。

另外還發現，大多數情況下 M32比M4快一些，證明了32的分塊尺寸是合適的。有興趣的讀者可以自己試試其他的尺寸。

4.3 4行、3倍向量寬度、ijk順序的分塊算法（`BlockM4Nv3_ikj_M32`、`BlockM4Nv3_ikj_M32Parallel`、`BlockM4Nv3_ikj_M4`、`BlockM4Nv3_ikj_M4Parallel`）

sgemm_hsw 是一個用匯編語言編寫的高性能矩陣乘法程序。它的關鍵改進是采用了3倍向量寬度的列數。

為什么3倍向量寬度是更好的選擇呢？這與向量寄存器的數量有關。我們來梳理一下內循環需使用多少個向量寄存器——

首先看C矩陣：因現在每次處理4行，于是在3倍向量寬度時，共需 4*3=12 個寄存器。
隨后看B矩陣：C矩陣處理下一行的數據時，B矩陣還在同一行，故僅需跟列數匹配的向量寄存器就行了。在3倍向量寬度時，共需 3個寄存器。
隨后看A矩陣：每次僅需讀取一個浮點值，廣播到1個向量寄存器里。故僅需1個向量寄存器。

由于FMA指令能夠節省寄存器，沒有保存中間結果的寄存器開銷。故總共需要 12 + 3 + 1 = 16 的向量寄存器。

如今的X86處理器已經普及了AVX指令，它有16個向量寄存器。且Arm的AdvSimd指令集里，現在是最少16個向量寄存器。故上面的算法，正好能將這16個向量寄存器充分利用。

接下來我們用 C# 語言來實現這個算法，并進行基準測試。

4.3.1 公共方法的改進

為了簡化"一次性讀寫3個向量的操作"，VectorHelper 增加了這些公共方法。

[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static void LoadX3Unsafe<T>(ref readonly T source, out Vector<T> data0, out Vector<T> data1, out Vector<T> data2)
#if VECTOR_WHERE_STRUCT
        where T : struct
#endif // VECTOR_WHERE_STRUCT
        {
    ref Vector<T> p = ref Unsafe.As<T, Vector<T>>(ref Unsafe.AsRef(in source));
    data0 = p;
    data1 = Unsafe.Add(ref p, 1);
    data2 = Unsafe.Add(ref p, 2);
}

[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static void StoreX3Unsafe<T>(ref T destination, Vector<T> data0, Vector<T> data1, Vector<T> data2)
#if VECTOR_WHERE_STRUCT
        where T : struct
#endif // VECTOR_WHERE_STRUCT
        {
    ref Vector<T> p = ref Unsafe.As<T, Vector<T>>(ref destination);
    p = data0;
    Unsafe.Add(ref p, 1) = data1;
    Unsafe.Add(ref p, 2) = data2;
}

4.3.2 矩陣乘法內核算法

隨后改進內核算法，讓它一次性處理3倍向量寬度。

private static void GemmKernelM4Nv3(int M, int N, int K, ref readonly TMy A, int strideA, ref readonly TMy B, int strideB, ref TMy C, int strideC) {
    const int blockM = 4;
    int vectorWidth = Vector<TMy>.Count;
    int blockN = vectorWidth * 3;
    if (0 != (M % blockM)) {
        throw new ArgumentException(string.Format("The M({0}) of block is not an integer multiple of {1}!", M, blockM));
    }
    if (0 != (N % blockN)) {
        throw new ArgumentException(string.Format("The N({0}) of block is not an integer multiple of {1}!", N, blockN));
    }
    // Matrix multiply.
    ref TMy pA0 = ref Unsafe.AsRef(in A);
    ref TMy pB0 = ref Unsafe.AsRef(in B);
    ref TMy pC0 = ref C;
    for (int i = 0; i < M; i += blockM) {
        ref TMy pCLine = ref pC0;
        for (int j = 0; j < N; j += blockN) {
            ref TMy pC = ref pCLine;
            Vector<TMy> c0_0, c0_1, c0_2;
            Vector<TMy> c1_0, c1_1, c1_2;
            Vector<TMy> c2_0, c2_1, c2_2;
            Vector<TMy> c3_0, c3_1, c3_2;
            VectorHelper.LoadX3Unsafe(ref pC, out c0_0, out c0_1, out c0_2); pC = ref Unsafe.Add(ref pC, strideC);
            VectorHelper.LoadX3Unsafe(ref pC, out c1_0, out c1_1, out c1_2); pC = ref Unsafe.Add(ref pC, strideC);
            VectorHelper.LoadX3Unsafe(ref pC, out c2_0, out c2_1, out c2_2); pC = ref Unsafe.Add(ref pC, strideC);
            VectorHelper.LoadX3Unsafe(ref pC, out c3_0, out c3_1, out c3_2);
            // Add.
            ref TMy pALine = ref pA0;
            ref TMy pB = ref Unsafe.Add(ref pB0, j);
            for (int k = 0; k < K; ++k) {
                // pC += pA * pB;
                Vector<TMy> b0, b1, b2;
                Vector<TMy> va;
                VectorHelper.LoadX3Unsafe(ref pB, out b0, out b1, out b2);
                ref TMy pA = ref pALine;
                va = new Vector<TMy>(pA); c0_0 = VectorHelper.MultiplyAdd(va, b0, c0_0); c0_1 = VectorHelper.MultiplyAdd(va, b1, c0_1); c0_2 = VectorHelper.MultiplyAdd(va, b2, c0_2); pA = ref Unsafe.Add(ref pA, strideA);
                va = new Vector<TMy>(pA); c1_0 = VectorHelper.MultiplyAdd(va, b0, c1_0); c1_1 = VectorHelper.MultiplyAdd(va, b1, c1_1); c1_2 = VectorHelper.MultiplyAdd(va, b2, c1_2); pA = ref Unsafe.Add(ref pA, strideA);
                va = new Vector<TMy>(pA); c2_0 = VectorHelper.MultiplyAdd(va, b0, c2_0); c2_1 = VectorHelper.MultiplyAdd(va, b1, c2_1); c2_2 = VectorHelper.MultiplyAdd(va, b2, c2_2); pA = ref Unsafe.Add(ref pA, strideA);
                va = new Vector<TMy>(pA); c3_0 = VectorHelper.MultiplyAdd(va, b0, c3_0); c3_1 = VectorHelper.MultiplyAdd(va, b1, c3_1); c3_2 = VectorHelper.MultiplyAdd(va, b2, c3_2);
                // Next.
                pALine = ref Unsafe.Add(ref pALine, 1);
                pB = ref Unsafe.Add(ref pB, strideB);
            }
            // Store.
            pC = ref pCLine;
            VectorHelper.StoreX3Unsafe(ref pC, c0_0, c0_1, c0_2); pC = ref Unsafe.Add(ref pC, strideC);
            VectorHelper.StoreX3Unsafe(ref pC, c1_0, c1_1, c1_2); pC = ref Unsafe.Add(ref pC, strideC);
            VectorHelper.StoreX3Unsafe(ref pC, c2_0, c2_1, c2_2); pC = ref Unsafe.Add(ref pC, strideC);
            VectorHelper.StoreX3Unsafe(ref pC, c3_0, c3_1, c3_2);
            // Next.
            pCLine = ref Unsafe.Add(ref pCLine, blockN);
        }
        pA0 = ref Unsafe.Add(ref pA0, strideA * blockM);
        pC0 = ref Unsafe.Add(ref pC0, strideC * blockM);
    }
}

4.3.3 矩陣乘法完整算法

因內核算法現在是 3倍向量寬度，導致它無法覆蓋尺寸是“2的整數冪”的矩陣。例如 1024 無法被3整除。

而尺寸是“2的整數冪”的矩陣是經常使用的，故需想辦法支持它。

可以采用這個辦法——優先用GemmKernelM4Nv3處理數據，剩余數據用GemmKernelM4Nv1處理。于是RunByI的里面有2個j循環，且實現計算好了各自的循環次數。

internal unsafe static void StaticBlockM4Nv3_ikj(int M, int N, int K, ref readonly TMy A, int strideA, ref readonly TMy B, int strideB, ref TMy C, int strideC, int blockM, int blockN, int blockK, bool allowParallel = false) {
    int vectorWidth = Vector<TMy>.Count;
    int vectorWidth3 = vectorWidth * 3;
    if (0 != (M % blockM)) {
        throw new ArgumentException(string.Format("The M({0}) is not an integer multiple of {1}!", M, blockM));
    }
    if (blockN < vectorWidth3) {
        throw new ArgumentException(string.Format("The blockN({0}) is less {1}!", blockN, vectorWidth3));
    }
    if (0 != (K % blockK)) {
        throw new ArgumentException(string.Format("The K({0}) is not an integer multiple of {1}!", K, blockK));
    }
    int blockN3 = (blockN / vectorWidth3) * vectorWidth3;
    int n;
    int nEnd3;
    int nEnd1;
    n = N / blockN3;
    nEnd3 = n * blockN3;
    n = (N - nEnd3) / vectorWidth;
    nEnd1 = nEnd3 + n * vectorWidth;
    if (nEnd1 != N) {
        throw new ArgumentException(string.Format("The N({0}) is not an integer multiple of {1}!", N, vectorWidth));
    }
    // Clear matrix C.
    MatrixUtil.Fill((TMy)0, M, N, ref C, strideC);
    // Body.
    int strideB_blockK = strideB * blockK;
    ref TMy pA0 = ref Unsafe.AsRef(in A);
    ref TMy pB0 = ref Unsafe.AsRef(in B);
    if (allowParallel) {
        fixed (TMy* pA = &pA0, pB = &pB0, pC = &C) {
            nint addressA = (nint)pA;
            nint addressB = (nint)pB;
            nint addressC = (nint)pC;
            int cnt = M / blockM;
            Parallel.For(0, cnt, idx => {
                int i = idx * blockM;
                ref TMy refA = ref Unsafe.AsRef<TMy>((void*)addressA);
                ref TMy refB = ref Unsafe.AsRef<TMy>((void*)addressB);
                ref TMy refC = ref Unsafe.AsRef<TMy>((void*)addressC);
                RunByI(M, N, K, ref refA, strideA, ref refB, strideB, ref refC, strideC, i);
            });
        }
    } else {
        for (int i = 0; i < M; i += blockM) {
            RunByI(M, N, K, ref pA0, strideA, ref pB0, strideB, ref C, strideC, i);
        }
    }

    void RunByI(int M, int N, int K, ref TMy A, int strideA, ref TMy B, int strideB, ref TMy C, int strideC, int i) {
        ref TMy pALine = ref Unsafe.Add(ref A, strideA * i);
        ref TMy pCLine = ref Unsafe.Add(ref C, strideC * i);
        ref TMy pBLine = ref B;
        for (int k = 0; k < K; k += blockK) {
            ref TMy pB = ref pBLine;
            ref TMy pC = ref pCLine;
            int j = 0;
            for (; j < nEnd3; j += blockN3) {
                GemmKernelM4Nv3(blockM, blockN3, blockK, in pALine, strideA, in pB, strideB, ref pC, strideC);
                // Next.
                pB = ref Unsafe.Add(ref pB, blockN3);
                pC = ref Unsafe.Add(ref pC, blockN3);
            }
            for (; j < nEnd1; j += vectorWidth) {
                GemmKernelM4Nv1(blockM, vectorWidth, blockK, in pALine, strideA, in pB, strideB, ref pC, strideC);
                // Next.
                pB = ref Unsafe.Add(ref pB, vectorWidth);
                pC = ref Unsafe.Add(ref pC, vectorWidth);
            }
            // Next.
            pALine = ref Unsafe.Add(ref pALine, blockK);
            pBLine = ref Unsafe.Add(ref pBLine, strideB_blockK);
        }
    }
}

internal static void StaticBlockM4Nv3_ikj_M32(int M, int N, int K, ref readonly TMy A, int strideA, ref readonly TMy B, int strideB, ref TMy C, int strideC, bool allowParallel = false) {
    //int blockN = 32;
    int blockN = Vector<TMy>.Count * 3 * 4;
    if (blockN > N) {
        blockN = N;
    }
    StaticBlockM4Nv3_ikj(M, N, K, in A, strideA, in B, strideB, ref C, strideC, 32, blockN, CommonBlockK, allowParallel);
}

internal static void StaticBlockM4Nv3_ikj_M4(int M, int N, int K, ref readonly TMy A, int strideA, ref readonly TMy B, int strideB, ref TMy C, int strideC, bool allowParallel = false) {
    //int blockN = 32;
    int blockN = Vector<TMy>.Count * 3 * 4;
    if (blockN > N) {
        blockN = N;
    }
    StaticBlockM4Nv3_ikj(M, N, K, in A, strideA, in B, strideB, ref C, strideC, 4, blockN, CommonBlockK, allowParallel);
}

此時也提供了 M4、M32這2種分塊策略的方法。

4.3.4 基準測試方法

對于上面的方法，它的基準測試代碼如下。

[Benchmark]
public void BlockM4Nv3_ikj_M4() {
    StaticBlockM4Nv3_ikj_M4(MatrixM, MatrixN, MatrixK, ref arrayA![0], StrideA, ref arrayB![0], StrideB, ref arrayC![0], StrideC);
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("BlockM4Nv3_ikj_M4");
    }
}

[Benchmark]
public void BlockM4Nv3_ikj_M4Parallel() {
    StaticBlockM4Nv3_ikj_M4(MatrixM, MatrixN, MatrixK, ref arrayA![0], StrideA, ref arrayB![0], StrideB, ref arrayC![0], StrideC, true);
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("BlockM4Nv3_ikj_M4Parallel");
    }
}

[Benchmark]
public void BlockM4Nv3_ikj_M32() {
    StaticBlockM4Nv3_ikj_M32(MatrixM, MatrixN, MatrixK, ref arrayA![0], StrideA, ref arrayB![0], StrideB, ref arrayC![0], StrideC);
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("BlockM4Nv3_ikj_M32");
    }
}

[Benchmark]
public void BlockM4Nv3_ikj_M32Parallel() {
    StaticBlockM4Nv3_ikj_M32(MatrixM, MatrixN, MatrixK, ref arrayA![0], StrideA, ref arrayB![0], StrideB, ref arrayC![0], StrideC, true);
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("BlockM4Nv3_ikj_M32Parallel");
    }
}

4.3.5 基準測試結果

基準測試結果如下。

Method	N	Mean	Error	StdDev	Median	Ratio	RatioSD	Code Size
Basic	1024	4,712,905,103.3 ns	35,792,824.68 ns	53,573,019.05 ns	4,722,569,850.0 ns	1.000	0.02	954 B
BlockM4Nv3_ikj_M4	1024	52,756,227.9 ns	1,133,938.16 ns	1,626,260.36 ns	53,519,345.5 ns	0.011	0.00	3,766 B
BlockM4Nv3_ikj_M4Parallel	1024	6,234,993.0 ns	450,007.94 ns	645,388.00 ns	5,976,738.7 ns	0.001	0.00	10,419 B
BlockM4Nv3_ikj_M32	1024	51,007,023.1 ns	1,010,156.07 ns	1,448,735.77 ns	51,688,581.8 ns	0.011	0.00	3,819 B
BlockM4Nv3_ikj_M32Parallel	1024	5,851,851.6 ns	266,588.14 ns	390,761.47 ns	5,628,710.9 ns	0.001	0.00	10,563 B

對測試結果進行對比——

BlockM4Nv3_ikj_M4: 耗時 52,756,227.9 ns, 故 GFOPS 為 2 / 0.0527562279 ≈ 37.91, 性能是Basic的 4,712,905,103.3 / 52,756,227.9 ≈ 89.33 倍.
BlockM4Nv3_ikj_M4Parallel: 耗時 6,234,993.0 ns, 故 GFOPS 為 2 / 0.0062349930 ≈ 320.77, 性能是Basic的 4,712,905,103.3 / 6,234,993.0 ≈ 755.88 倍.
BlockM4Nv3_ikj_M32: 耗時 51,007,023.1 ns, 故 GFOPS 為 2 / 0.0510070231 ≈ 39.21, 性能是Basic的 4,712,905,103.3 / 51,007,023.1 ≈ 92.40 倍.
BlockM4Nv3_ikj_M32Parallel: 耗時 5,851,851.6 ns, 故 GFOPS 為 2 / 0.0058518516 ≈ 341.77, 性能是Basic的 4,712,905,103.3 / 5,851,851.6 ≈ 805.37 倍.

性能最好的是 BlockM4Nv3_ikj_M32Parallel，它性能是Basic的 805.37 倍。且它突破了 TileRowSimdFmaParallel 407.12倍的記錄。

4.4 4行、3倍512位向量寬度、ijk順序的分塊算法（`BlockM4Nv3On512_ikj_M32`、`BlockM4Nv3On512_ikj_M32Parallel`、`BlockM4Nv3On512_ikj_M4`、`BlockM4Nv3On512_ikj_M4Parallel`）

目前 MKL、OpenBLAS 都使用了 AVX-512指令集優化。
在 .NET 8.0 開始，C# 也能是用 AVX-512指令集了。大多數情況時，使用 Vector512 靜態類的方法，會更加方便——對于大多數代碼，僅需將 Vector 替換為 Vector512。

4.4.1 公共方法的改進

Vector512 也需要 LoadX3Unsafe等公共方法。于是新增了Vector512Helper類，增加了這些公共方法。

[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static void LoadX3Unsafe<T>(ref readonly T source, out Vector512<T> data0, out Vector512<T> data1, out Vector512<T> data2)
#if VECTOR_WHERE_STRUCT
        where T : struct
#endif // VECTOR_WHERE_STRUCT
        {
    ref Vector512<T> p = ref Unsafe.As<T, Vector512<T>>(ref Unsafe.AsRef(in source));
    data0 = p;
    data1 = Unsafe.Add(ref p, 1);
    data2 = Unsafe.Add(ref p, 2);
}

[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static void StoreX3Unsafe<T>(ref T destination, Vector512<T> data0, Vector512<T> data1, Vector512<T> data2)
#if VECTOR_WHERE_STRUCT
        where T : struct
#endif // VECTOR_WHERE_STRUCT
        {
    ref Vector512<T> p = ref Unsafe.As<T, Vector512<T>>(ref destination);
    p = data0;
    Unsafe.Add(ref p, 1) = data1;
    Unsafe.Add(ref p, 2) = data2;
}

[MethodImpl(MethodImplOptions.AggressiveInlining)]
public static Vector512<float> MultiplyAdd(Vector512<float> left, Vector512<float> right, Vector512<float> addend) {
#if NET9_0_OR_GREATER
    return Vector512.FusedMultiplyAdd(left, right, addend);
#else
    return Vector512.Add(addend, Vector512.Multiply(left, right));
#endif // NET9_0_OR_GREATER
}

4.4.2 矩陣乘法內核算法

僅需將 Vector 改為 Vector512，便能實現 GemmKernelM4Nv3On512。

private static void GemmKernelM4Nv3On512(int M, int N, int K, ref readonly TMy A, int strideA, ref readonly TMy B, int strideB, ref TMy C, int strideC) {
    const int blockM = 4;
    int vectorWidth = Vector512<TMy>.Count;
    int blockN = vectorWidth * 3;
    if (BenchmarkUtil.IsLastRun) {
        Volatile.Write(ref blockN, 0);
        //Debugger.Break();
    }
    blockN = vectorWidth * 3;
    if (0 != (M % blockM)) {
        throw new ArgumentException(string.Format("The M({0}) of block is not an integer multiple of {1}!", M, blockM));
    }
    if (0 != (N % blockN)) {
        throw new ArgumentException(string.Format("The N({0}) of block is not an integer multiple of {1}!", N, blockN));
    }
    // Matrix multiply.
    ref TMy pA0 = ref Unsafe.AsRef(in A);
    ref TMy pB0 = ref Unsafe.AsRef(in B);
    ref TMy pC0 = ref C;
    for (int i = 0; i < M; i += blockM) {
        ref TMy pCLine = ref pC0;
        for (int j = 0; j < N; j += blockN) {
            ref TMy pC = ref pCLine;
            Vector512<TMy> c0_0, c0_1, c0_2;
            Vector512<TMy> c1_0, c1_1, c1_2;
            Vector512<TMy> c2_0, c2_1, c2_2;
            Vector512<TMy> c3_0, c3_1, c3_2;
            Vector512Helper.LoadX3Unsafe(ref pC, out c0_0, out c0_1, out c0_2); pC = ref Unsafe.Add(ref pC, strideC);
            Vector512Helper.LoadX3Unsafe(ref pC, out c1_0, out c1_1, out c1_2); pC = ref Unsafe.Add(ref pC, strideC);
            Vector512Helper.LoadX3Unsafe(ref pC, out c2_0, out c2_1, out c2_2); pC = ref Unsafe.Add(ref pC, strideC);
            Vector512Helper.LoadX3Unsafe(ref pC, out c3_0, out c3_1, out c3_2);
            // Add.
            ref TMy pALine = ref pA0;
            ref TMy pB = ref Unsafe.Add(ref pB0, j);
            for (int k = 0; k < K; ++k) {
                // pC += pA * pB;
                Vector512<TMy> b0, b1, b2;
                Vector512<TMy> va;
                Vector512Helper.LoadX3Unsafe(ref pB, out b0, out b1, out b2);
                ref TMy pA = ref pALine;
                va = Vector512.Create(pA); c0_0 = Vector512Helper.MultiplyAdd(va, b0, c0_0); c0_1 = Vector512Helper.MultiplyAdd(va, b1, c0_1); c0_2 = Vector512Helper.MultiplyAdd(va, b2, c0_2); pA = ref Unsafe.Add(ref pA, strideA);
                va = Vector512.Create(pA); c1_0 = Vector512Helper.MultiplyAdd(va, b0, c1_0); c1_1 = Vector512Helper.MultiplyAdd(va, b1, c1_1); c1_2 = Vector512Helper.MultiplyAdd(va, b2, c1_2); pA = ref Unsafe.Add(ref pA, strideA);
                va = Vector512.Create(pA); c2_0 = Vector512Helper.MultiplyAdd(va, b0, c2_0); c2_1 = Vector512Helper.MultiplyAdd(va, b1, c2_1); c2_2 = Vector512Helper.MultiplyAdd(va, b2, c2_2); pA = ref Unsafe.Add(ref pA, strideA);
                va = Vector512.Create(pA); c3_0 = Vector512Helper.MultiplyAdd(va, b0, c3_0); c3_1 = Vector512Helper.MultiplyAdd(va, b1, c3_1); c3_2 = Vector512Helper.MultiplyAdd(va, b2, c3_2);
                // Next.
                pALine = ref Unsafe.Add(ref pALine, 1);
                pB = ref Unsafe.Add(ref pB, strideB);
            }
            // Store.
            pC = ref pCLine;
            Vector512Helper.StoreX3Unsafe(ref pC, c0_0, c0_1, c0_2); pC = ref Unsafe.Add(ref pC, strideC);
            Vector512Helper.StoreX3Unsafe(ref pC, c1_0, c1_1, c1_2); pC = ref Unsafe.Add(ref pC, strideC);
            Vector512Helper.StoreX3Unsafe(ref pC, c2_0, c2_1, c2_2); pC = ref Unsafe.Add(ref pC, strideC);
            Vector512Helper.StoreX3Unsafe(ref pC, c3_0, c3_1, c3_2);
            // Next.
            pCLine = ref Unsafe.Add(ref pCLine, blockN);
        }
        pA0 = ref Unsafe.Add(ref pA0, strideA * blockM);
        pC0 = ref Unsafe.Add(ref pC0, strideC * blockM);
    }
}

4.4.3 矩陣乘法完整算法

可以將大片區域的數據交給 GemmKernelM4Nv3On512 處理，而尾部剩余交給 GemmKernelM4Nv1 處理，這便能支持各種“2的冪次”的矩陣。

internal unsafe static void StaticBlockM4Nv3On512_ikj(int M, int N, int K, ref readonly TMy A, int strideA, ref readonly TMy B, int strideB, ref TMy C, int strideC, int blockM, int blockN, int blockK, bool allowParallel = false) {
    if (!Vector512.IsHardwareAccelerated || !Vector512<TMy>.IsSupported) {
        throw new NotSupportedException("Vector512.IsHardwareAccelerated is false!");
    }
    int vectorWidth = Vector<TMy>.Count;
    int vectorWidth3 = Vector512<TMy>.Count * 3;
    if (0 != (M % blockM)) {
        throw new ArgumentException(string.Format("The M({0}) is not an integer multiple of {1}!", M, blockM));
    }
    if (blockN < vectorWidth3) {
        throw new ArgumentException(string.Format("The blockN({0}) is less {1}!", blockN, vectorWidth3));
    }
    if (0 != (K % blockK)) {
        throw new ArgumentException(string.Format("The K({0}) is not an integer multiple of {1}!", K, blockK));
    }
    int blockN3 = (blockN / vectorWidth3) * vectorWidth3;
    int n;
    int nEnd3;
    int nEnd1;
    n = N / blockN3;
    nEnd3 = n * blockN3;
    n = (N - nEnd3) / vectorWidth;
    nEnd1 = nEnd3 + n * vectorWidth;
    if (nEnd1 != N) {
        throw new ArgumentException(string.Format("The N({0}) is not an integer multiple of {1}!", N, vectorWidth));
    }
    // Clear matrix C.
    MatrixUtil.Fill((TMy)0, M, N, ref C, strideC);
    // Body.
    int strideB_blockK = strideB * blockK;
    ref TMy pA0 = ref Unsafe.AsRef(in A);
    ref TMy pB0 = ref Unsafe.AsRef(in B);
    if (allowParallel) {
        fixed (TMy* pA = &pA0, pB = &pB0, pC = &C) {
            nint addressA = (nint)pA;
            nint addressB = (nint)pB;
            nint addressC = (nint)pC;
            int cnt = M / blockM;
            Parallel.For(0, cnt, idx => {
                int i = idx * blockM;
                ref TMy refA = ref Unsafe.AsRef<TMy>((void*)addressA);
                ref TMy refB = ref Unsafe.AsRef<TMy>((void*)addressB);
                ref TMy refC = ref Unsafe.AsRef<TMy>((void*)addressC);
                RunByI(M, N, K, ref refA, strideA, ref refB, strideB, ref refC, strideC, i);
            });
        }
    } else {
        for (int i = 0; i < M; i += blockM) {
            RunByI(M, N, K, ref pA0, strideA, ref pB0, strideB, ref C, strideC, i);
        }
    }

    void RunByI(int M, int N, int K, ref TMy A, int strideA, ref TMy B, int strideB, ref TMy C, int strideC, int i) {
        ref TMy pALine = ref Unsafe.Add(ref A, strideA * i);
        ref TMy pCLine = ref Unsafe.Add(ref C, strideC * i);
        ref TMy pBLine = ref B;
        for (int k = 0; k < K; k += blockK) {
            ref TMy pB = ref pBLine;
            ref TMy pC = ref pCLine;
            int j = 0;
            for (; j < nEnd3; j += blockN3) {
                GemmKernelM4Nv3On512(blockM, blockN3, blockK, in pALine, strideA, in pB, strideB, ref pC, strideC);
                // Next.
                pB = ref Unsafe.Add(ref pB, blockN3);
                pC = ref Unsafe.Add(ref pC, blockN3);
            }
            for (; j < nEnd1; j += vectorWidth) {
                GemmKernelM4Nv1(blockM, vectorWidth, blockK, in pALine, strideA, in pB, strideB, ref pC, strideC);
                // Next.
                pB = ref Unsafe.Add(ref pB, vectorWidth);
                pC = ref Unsafe.Add(ref pC, vectorWidth);
            }
            // Next.
            pALine = ref Unsafe.Add(ref pALine, blockK);
            pBLine = ref Unsafe.Add(ref pBLine, strideB_blockK);
        }
    }
}

internal static void StaticBlockM4Nv3On512_ikj_M32(int M, int N, int K, ref readonly TMy A, int strideA, ref readonly TMy B, int strideB, ref TMy C, int strideC, bool allowParallel = false) {
    //int blockN = 32;
    int blockN = Vector512<TMy>.Count * 3 * 4;
    if (blockN > N) {
        blockN = N;
    }
    StaticBlockM4Nv3On512_ikj(M, N, K, in A, strideA, in B, strideB, ref C, strideC, 32, blockN, CommonBlockK, allowParallel);
}

internal static void StaticBlockM4Nv3On512_ikj_M4(int M, int N, int K, ref readonly TMy A, int strideA, ref readonly TMy B, int strideB, ref TMy C, int strideC, bool allowParallel = false) {
    //int blockN = 32;
    int blockN = Vector512<TMy>.Count * 3 * 4;
    if (blockN > N) {
        blockN = N;
    }
    StaticBlockM4Nv3On512_ikj(M, N, K, in A, strideA, in B, strideB, ref C, strideC, 4, blockN, CommonBlockK, allowParallel);
}

4.4.4 基準測試方法

對于上面的方法，它的基準測試代碼如下。

#if NET8_0_OR_GREATER
[Benchmark]
public void BlockM4Nv3On512_ikj_M4() {
    StaticBlockM4Nv3On512_ikj_M4(MatrixM, MatrixN, MatrixK, ref arrayA![0], StrideA, ref arrayB![0], StrideB, ref arrayC![0], StrideC);
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("BlockM4Nv3On512_ikj_M4");
    }
}

[Benchmark]
public void BlockM4Nv3On512_ikj_M4Parallel() {
    StaticBlockM4Nv3On512_ikj_M4(MatrixM, MatrixN, MatrixK, ref arrayA![0], StrideA, ref arrayB![0], StrideB, ref arrayC![0], StrideC, true);
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("BlockM4Nv3On512_ikj_M4Parallel");
    }
}

[Benchmark]
public void BlockM4Nv3On512_ikj_M32() {
    if (BenchmarkUtil.IsLastRun) {
        Volatile.Write(ref dstTMy, 0);
        //Debugger.Break();
    }
    StaticBlockM4Nv3On512_ikj_M32(MatrixM, MatrixN, MatrixK, ref arrayA![0], StrideA, ref arrayB![0], StrideB, ref arrayC![0], StrideC);
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("BlockM4Nv3On512_ikj_M32");
    }
}

[Benchmark]
public void BlockM4Nv3On512_ikj_M32Parallel() {
    StaticBlockM4Nv3On512_ikj_M32(MatrixM, MatrixN, MatrixK, ref arrayA![0], StrideA, ref arrayB![0], StrideB, ref arrayC![0], StrideC, true);
    if (CheckMode) {
        dstTMy = GetCheckSum();
        CheckResult("BlockM4Nv3On512_ikj_M32Parallel");
    }
}
#endif // NET8_0_OR_GREATER

4.4.5 基準測試結果

基準測試結果如下。

Method	N	Mean	Error	StdDev	Median	Ratio	RatioSD	Code Size
Basic	1024	4,712,905,103.3 ns	35,792,824.68 ns	53,573,019.05 ns	4,722,569,850.0 ns	1.000	0.02	954 B
BlockM4Nv3On512_ikj_M4	1024	44,685,858.1 ns	4,745,584.17 ns	6,652,646.79 ns	41,372,192.9 ns	0.009	0.00	3,835 B
BlockM4Nv3On512_ikj_M4Parallel	1024	4,842,750.9 ns	306,368.06 ns	429,485.26 ns	4,669,524.2 ns	0.001	0.00	10,499 B
BlockM4Nv3On512_ikj_M32	1024	32,179,510.0 ns	206,091.41 ns	275,126.14 ns	32,157,606.2 ns	0.007	0.00	3,666 B
BlockM4Nv3On512_ikj_M32Parallel	1024	4,363,112.2 ns	73,021.25 ns	97,481.28 ns	4,339,956.2 ns	0.001	0.00	10,848 B
UseMathNet	1024	53,205,723.8 ns	836,527.21 ns	1,226,170.84 ns	52,803,610.0 ns	0.011	0.00	7,575 B
UseOpenBLAS	1024	2,932,070.9 ns	117,359.68 ns	160,643.26 ns	2,864,316.2 ns	0.001	0.00	NA
UseMKL	1024	4,379,927.2 ns	58,880.02 ns	88,128.84 ns	4,340,348.8 ns	0.001	0.00	508 B

對測試結果進行對比——

BlockM4Nv3On512_ikj_M4: 耗時 44,685,858.1 ns, 故 GFOPS 為 2 / 0.0446858581 ≈ 44.76, 性能是Basic的 4,712,905,103.3 / 44,685,858.1 ≈ 105.47 倍.
BlockM4Nv3On512_ikj_M4Parallel: 耗時 4,842,750.9 ns, 故 GFOPS 為 2 / 0.0048427509 ≈ 412.99, 性能是Basic的 4,712,905,103.3 / 4,842,750.9 ≈ 973.19 倍.
BlockM4Nv3On512_ikj_M32: 耗時 32,179,510.0 ns, 故 GFOPS 為 2 / 0.0321795100 ≈ 62.15, 性能是Basic的 4,712,905,103.3 / 32,179,510.0 ≈ 146.46 倍.
BlockM4Nv3On512_ikj_M32Parallel: 耗時 4,363,112.2 ns, 故 GFOPS 為 2 / 0.0043631122 ≈ 458.39, 性能是Basic的 4,712,905,103.3 / 4,363,112.2 ≈ 1080.17 倍.
UseMathNet: 耗時 53,205,723.8 ns, 故 GFOPS 為 2 / 0.0532057238 ≈ 37.59, 性能是Basic的 4,712,905,103.3 / 53,205,723.8 ≈ 88.58 倍.
UseOpenBLAS: 耗時 2,932,070.9 ns, 故 GFOPS 為 2 / 0.0029320709 ≈ 682.11, 性能是Basic的 4,712,905,103.3 / 2,932,070.9 ≈ 1607.36 倍.
UseMKL: 耗時 4,379,927.2 ns, 故 GFOPS 為 2 / 0.0043799272 ≈ 456.63, 性能是Basic的 4,712,905,103.3 / 4,379,927.2 ≈ 1076.02 倍.

此時性能最好的并行算法是BlockM4Nv3On512_ikj_M32Parallel，它的性能是Basic的 1080.17 倍。而 MKL是 1076.02 倍，即該算法一般比MKL還稍微快一點。該算法比起 OpenBLAS ，差距在1倍以內，可看作同一梯隊。

此時性能最好的單線程算法是BlockM4Nv3On512_ikj_M32，它的性能是Basic的 146.46 倍，超過了具有并行計算加速的UseMathNet。這說明算法很重要，否則并行計算加速的程序性能，有可能會被單線程程序超過。

五、基準測試結果

現代 .NET的跨平臺功能非常成熟，能跨平臺使用SIMD硬件加速。本章進行全面的基準測試，分別測試 X86、Arm處理器的性能。且不僅會測試Single類型，還會測試 Double類型的性能。

5.1 X86 架構 - .NET 9.0

當前CPU是 “AMD Ryzen 7 7840H”，操作系統是 “Windows 11”。

5.1.1 Single（單精度浮點型）

X86架構上、.NET 9.0 程序、Single類型的基準測試結果如下。

BenchmarkDotNet v0.15.2, Windows 11 (10.0.26100.4946/24H2/2024Update/HudsonValley)
AMD Ryzen 7 7840H w/ Radeon 780M Graphics 3.80GHz, 1 CPU, 16 logical and 8 physical cores
.NET SDK 9.0.301
  [Host]    : .NET 9.0.6 (9.0.625.26613), X64 AOT AVX-512F+CD+BW+DQ+VL+VBMI
  MediumRun : .NET 9.0.6 (9.0.625.26613), X64 RyuJIT AVX-512F+CD+BW+DQ+VL+VBMI

Method	N	Mean	Error	StdDev	Median	Ratio	RatioSD	Code Size
Basic	1024	4,712,905,103.3 ns	35,792,824.68 ns	53,573,019.05 ns	4,722,569,850.0 ns	1.000	0.02	954 B
TileRow	1024	780,626,575.0 ns	5,970,550.33 ns	8,562,785.59 ns	778,917,250.0 ns	0.166	0.00	1,238 B
TileRowSpan	1024	613,236,262.1 ns	6,326,567.15 ns	9,273,400.86 ns	610,494,600.0 ns	0.130	0.00	1,358 B
TileRowRef	1024	332,063,973.2 ns	4,375,391.05 ns	6,275,055.62 ns	329,953,500.0 ns	0.070	0.00	1,512 B
TileRowSimd	1024	71,736,249.5 ns	2,768,453.89 ns	3,880,986.03 ns	69,775,500.0 ns	0.015	0.00	1,258 B
TileRowSimdFmaBcl	1024	71,320,997.3 ns	1,540,394.38 ns	2,056,382.42 ns	70,551,614.3 ns	0.015	0.00	1,262 B
TileRowSimdFma	1024	72,957,369.2 ns	3,088,652.97 ns	4,329,860.46 ns	71,072,300.0 ns	0.015	0.00	1,262 B
TileRowSimdParallel	1024	11,576,096.3 ns	447,403.26 ns	669,652.19 ns	11,727,672.3 ns	0.002	0.00	8,549 B
TileRowSimdFmaParallel	1024	12,234,503.5 ns	337,579.48 ns	505,273.12 ns	12,306,358.6 ns	0.003	0.00	8,565 B
BlockM4Nv1_ijk_M32	1024	155,479,981.2 ns	925,593.09 ns	1,327,458.06 ns	155,197,087.5 ns	0.033	0.00	NA
BlockM4Nv1_ijk_M32Parallel	1024	18,389,778.0 ns	391,156.50 ns	573,352.18 ns	18,200,718.8 ns	0.004	0.00	NA
BlockM4Nv1_ikj_M32	1024	158,203,231.7 ns	1,098,377.31 ns	1,643,999.58 ns	157,511,900.0 ns	0.034	0.00	2,303 B
BlockM4Nv1_ikj_M32Parallel	1024	15,417,779.4 ns	528,972.18 ns	775,360.62 ns	15,101,640.6 ns	0.003	0.00	9,453 B
BlockM4Nv1_ikj_M4	1024	159,175,464.8 ns	2,913,579.61 ns	4,084,432.04 ns	161,698,000.0 ns	0.034	0.00	2,188 B
BlockM4Nv1_ikj_M4Parallel	1024	17,944,453.9 ns	584,658.22 ns	856,984.51 ns	17,830,587.5 ns	0.004	0.00	9,311 B
BlockM4Nv3_ikj_M4	1024	52,756,227.9 ns	1,133,938.16 ns	1,626,260.36 ns	53,519,345.5 ns	0.011	0.00	3,766 B
BlockM4Nv3_ikj_M4Parallel	1024	6,234,993.0 ns	450,007.94 ns	645,388.00 ns	5,976,738.7 ns	0.001	0.00	10,419 B
BlockM4Nv3_ikj_M32	1024	51,007,023.1 ns	1,010,156.07 ns	1,448,735.77 ns	51,688,581.8 ns	0.011	0.00	3,819 B
BlockM4Nv3_ikj_M32Parallel	1024	5,851,851.6 ns	266,588.14 ns	390,761.47 ns	5,628,710.9 ns	0.001	0.00	10,563 B
BlockM4Nv3On512_ikj_M4	1024	44,685,858.1 ns	4,745,584.17 ns	6,652,646.79 ns	41,372,192.9 ns	0.009	0.00	3,835 B
BlockM4Nv3On512_ikj_M4Parallel	1024	4,842,750.9 ns	306,368.06 ns	429,485.26 ns	4,669,524.2 ns	0.001	0.00	10,499 B
BlockM4Nv3On512_ikj_M32	1024	32,179,510.0 ns	206,091.41 ns	275,126.14 ns	32,157,606.2 ns	0.007	0.00	3,666 B
BlockM4Nv3On512_ikj_M32Parallel	1024	4,363,112.2 ns	73,021.25 ns	97,481.28 ns	4,339,956.2 ns	0.001	0.00	10,848 B
UseMathNet	1024	53,205,723.8 ns	836,527.21 ns	1,226,170.84 ns	52,803,610.0 ns	0.011	0.00	7,575 B
UseOpenBLAS	1024	2,932,070.9 ns	117,359.68 ns	160,643.26 ns	2,864,316.2 ns	0.001	0.00	NA
UseMKL	1024	4,379,927.2 ns	58,880.02 ns	88,128.84 ns	4,340,348.8 ns	0.001	0.00	508 B

測試結果對比如下。

Method	耗時	GFOPS	性能倍數
Basic	4,712,905,103.3 ns	0.42	1.00
TileRow	780,626,575.0 ns	2.56	6.04
TileRowSpan	613,236,262.1 ns	3.26	7.69
TileRowRef	332,063,973.2 ns	6.02	14.19
TileRowSimd	71,736,249.5 ns	27.88	65.70
TileRowSimdFmaBcl	71,320,997.3 ns	28.04	66.08
TileRowSimdFma	72,957,369.2 ns	27.41	64.60
TileRowSimdParallel	11,576,096.3 ns	172.77	407.12
TileRowSimdFmaParallel	12,234,503.5 ns	163.47	385.21
BlockM4Nv1_ijk_M32	155,479,981.2 ns	12.86	30.31
BlockM4Nv1_ijk_M32Parallel	18,389,778.0 ns	108.76	256.28
BlockM4Nv1_ikj_M32	158,203,231.7 ns	12.64	29.79
BlockM4Nv1_ikj_M32Parallel	15,417,779.4 ns	129.72	305.68
BlockM4Nv1_ikj_M4	159,175,464.8 ns	12.56	29.61
BlockM4Nv1_ikj_M4Parallel	17,944,453.9 ns	111.46	262.64
BlockM4Nv3_ikj_M4	52,756,227.9 ns	37.91	89.33
BlockM4Nv3_ikj_M4Parallel	6,234,993.0 ns	320.77	755.88
BlockM4Nv3_ikj_M32	51,007,023.1 ns	39.21	92.40
BlockM4Nv3_ikj_M32Parallel	5,851,851.6 ns	341.77	805.37
BlockM4Nv3On512_ikj_M4	44,685,858.1 ns	44.76	105.47
BlockM4Nv3On512_ikj_M4Parallel	4,842,750.9 ns	412.99	973.19
BlockM4Nv3On512_ikj_M32	32,179,510.0 ns	62.15	146.46
BlockM4Nv3On512_ikj_M32Parallel	4,363,112.2 ns	458.39	1080.17
UseMathNet	53,205,723.8 ns	37.59	88.58
UseOpenBLAS	2,932,070.9 ns	682.11	1607.36
UseMKL	4,379,927.2 ns	456.63	1076.02

我們表現最好的算法是 BlockM4Nv3On512_ikj_M32Parallel，它的性能是基礎算法的 1080.17 倍（約為 1080），此時的每秒浮點計算次數是 458.39 GFOPS。

它的性能比 MKL 稍微快了一些。4,379,927.2 / 4,363,112.2 ≈ 1.003854，即快了 0.3854%。

且它與 OpenBLAS的差距在一倍以內，屬于同一梯隊。（2,932,070.9 / 4,363,112.2 ≈ 0.672013，即它能達到 OpenBLAS 67.2012% 的性能）

5.1.2 Double（雙精度浮點型）

通過巧妙地使用 using指令，本程序還能測試DGEMM（Double General Matrix Multiply，雙精度浮點數通用矩陣乘法）的性能。只是為了減少基準測試的時間，本程序默認關閉了它的基準測試。

若想測試 DGEMM，可以修改“MatrixNMultiplyBenchmark_Double.cs”，將第一行的 //#undef BENCHMARKS_OFF 去掉注釋（//），開啟DGEMM的測試。并修改“MatrixNMultiplyBenchmark_Single.cs”，將第一行的 #undef BENCHMARKS_OFF 的前面加注釋（//），關閉SGEMM的測試。

X86架構上、.NET 9.0 程序、Double類型的基準測試結果如下。

BenchmarkDotNet v0.15.2, Windows 11 (10.0.26100.4946/24H2/2024Update/HudsonValley)
AMD Ryzen 7 7840H w/ Radeon 780M Graphics 3.80GHz, 1 CPU, 16 logical and 8 physical cores
.NET SDK 9.0.301
  [Host]    : .NET 9.0.6 (9.0.625.26613), X64 AOT AVX-512F+CD+BW+DQ+VL+VBMI
  MediumRun : .NET 9.0.6 (9.0.625.26613), X64 RyuJIT AVX-512F+CD+BW+DQ+VL+VBMI

Method	N	Mean	Error	StdDev	Median	Ratio	RatioSD	Code Size
Basic	1024	4,667,707,243.3 ns	101,856,765.08 ns	152,454,422.51 ns	4,722,324,950.0 ns	1.001	0.05	955 B
TileRow	1024	785,539,882.8 ns	6,951,632.14 ns	10,189,613.10 ns	781,816,000.0 ns	0.168	0.01	1,238 B
TileRowSpan	1024	612,766,200.0 ns	5,098,750.48 ns	7,312,476.18 ns	611,489,700.0 ns	0.131	0.00	1,358 B
TileRowRef	1024	331,644,776.0 ns	7,293,618.64 ns	9,736,772.22 ns	329,782,100.0 ns	0.071	0.00	1,632 B
TileRowSimd	1024	175,592,405.9 ns	27,847,032.37 ns	39,037,653.46 ns	163,639,500.0 ns	0.038	0.01	946 B
TileRowSimdFmaBcl	1024	165,678,173.1 ns	5,407,093.39 ns	7,401,291.09 ns	163,372,412.5 ns	0.036	0.00	946 B
TileRowSimdFma	1024	164,456,937.7 ns	5,192,151.95 ns	6,931,374.30 ns	162,801,575.0 ns	0.035	0.00	946 B
TileRowSimdParallel	1024	27,533,111.2 ns	351,339.32 ns	525,868.19 ns	27,299,954.7 ns	0.006	0.00	8,146 B
TileRowSimdFmaParallel	1024	27,163,961.1 ns	474,347.60 ns	709,981.21 ns	26,996,106.2 ns	0.006	0.00	8,279 B
BlockM4Nv1_ijk_M32	1024	314,843,932.1 ns	13,838,266.66 ns	19,846,430.18 ns	329,845,200.0 ns	0.068	0.00	NA
BlockM4Nv1_ijk_M32Parallel	1024	34,141,308.7 ns	578,416.74 ns	865,747.01 ns	34,121,580.0 ns	0.007	0.00	NA
BlockM4Nv1_ikj_M32	1024	308,316,596.2 ns	1,245,009.33 ns	1,704,182.97 ns	308,077,750.0 ns	0.066	0.00	NA
BlockM4Nv1_ikj_M32Parallel	1024	29,421,452.7 ns	563,599.63 ns	843,569.46 ns	29,088,087.5 ns	0.006	0.00	9,392 B
BlockM4Nv1_ikj_M4	1024	332,366,150.0 ns	1,675,601.19 ns	2,293,582.02 ns	332,275,700.0 ns	0.071	0.00	NA
BlockM4Nv1_ikj_M4Parallel	1024	35,847,960.5 ns	352,075.27 ns	493,560.39 ns	35,929,240.0 ns	0.008	0.00	9,268 B
BlockM4Nv3_ikj_M4	1024	97,701,496.6 ns	4,138,544.95 ns	5,801,662.51 ns	98,073,216.7 ns	0.021	0.00	3,830 B
BlockM4Nv3_ikj_M4Parallel	1024	11,446,186.9 ns	446,374.98 ns	640,177.71 ns	11,182,593.0 ns	0.002	0.00	10,587 B
BlockM4Nv3_ikj_M32	1024	91,633,206.1 ns	1,885,472.12 ns	2,704,088.00 ns	91,787,078.6 ns	0.020	0.00	3,857 B
BlockM4Nv3_ikj_M32Parallel	1024	10,177,112.8 ns	351,523.74 ns	492,787.22 ns	9,954,175.0 ns	0.002	0.00	10,737 B
BlockM4Nv3On512_ikj_M4	1024	103,019,217.0 ns	1,234,728.32 ns	1,648,326.98 ns	102,917,933.3 ns	0.022	0.00	3,831 B
BlockM4Nv3On512_ikj_M4Parallel	1024	9,567,307.4 ns	314,506.73 ns	430,500.40 ns	9,411,418.8 ns	0.002	0.00	10,654 B
BlockM4Nv3On512_ikj_M32	1024	66,571,730.6 ns	722,460.47 ns	1,058,973.28 ns	66,147,812.5 ns	0.014	0.00	3,689 B
BlockM4Nv3On512_ikj_M32Parallel	1024	9,291,286.4 ns	267,082.18 ns	365,585.13 ns	9,083,106.2 ns	0.002	0.00	10,906 B
UseMathNet	1024	57,825,146.5 ns	823,123.70 ns	1,153,904.57 ns	57,571,922.2 ns	0.012	0.00	7,554 B
UseOpenBLAS	1024	5,834,910.0 ns	419,034.34 ns	600,966.58 ns	5,468,444.9 ns	0.001	0.00	NA
UseMKL	1024	13,417,242.3 ns	585,101.67 ns	857,634.51 ns	13,104,798.4 ns	0.003	0.00	508 B

測試結果對比如下。

Method	耗時	GFOPS	性能倍數
Basic	4,667,707,243.3 ns	0.43	1.00
TileRow	785,539,882.8 ns	2.55	5.94
TileRowSpan	612,766,200.0 ns	3.26	7.62
TileRowRef	331,644,776.0 ns	6.03	14.07
TileRowSimd	175,592,405.9 ns	11.39	26.58
TileRowSimdFmaBcl	165,678,173.1 ns	12.07	28.17
TileRowSimdFma	164,456,937.7 ns	12.16	28.38
TileRowSimdParallel	27,533,111.2 ns	72.64	169.53
TileRowSimdFmaParallel	27,163,961.1 ns	73.63	171.83
BlockM4Nv1_ijk_M32	314,843,932.1 ns	6.35	14.83
BlockM4Nv1_ijk_M32Parallel	34,141,308.7 ns	58.58	136.72
BlockM4Nv1_ikj_M32	308,316,596.2 ns	6.49	15.14
BlockM4Nv1_ikj_M32Parallel	29,421,452.7 ns	67.98	158.65
BlockM4Nv1_ikj_M4	332,366,150.0 ns	6.02	14.04
BlockM4Nv1_ikj_M4Parallel	35,847,960.5 ns	55.79	130.21
BlockM4Nv3_ikj_M4	97,701,496.6 ns	20.47	47.78
BlockM4Nv3_ikj_M4Parallel	11,446,186.9 ns	174.73	407.80
BlockM4Nv3_ikj_M32	91,633,206.1 ns	21.83	50.94
BlockM4Nv3_ikj_M32Parallel	10,177,112.8 ns	196.52	458.65
BlockM4Nv3On512_ikj_M4	103,019,217.0 ns	19.41	45.31
BlockM4Nv3On512_ikj_M4Parallel	9,567,307.4 ns	209.05	487.88
BlockM4Nv3On512_ikj_M32	66,571,730.6 ns	30.04	70.12
BlockM4Nv3On512_ikj_M32Parallel	9,291,286.4 ns	215.26	502.37
UseMathNet	57,825,146.5 ns	34.59	80.72
UseOpenBLAS	5,834,910.0 ns	342.76	799.96
UseMKL	13,417,242.3 ns	149.06	347.89

我們表現最好的算法是 BlockM4Nv3On512_ikj_M32Parallel，它的性能是基礎算法的 502.37 倍，此時的每秒浮點計算次數是 215.26 GFOPS。

它的性能比 MKL 強了不少。13,417,242.3 / 9,291,286.4 ≈ 1.444067，即快了 44.4067%。

且它與 OpenBLAS的差距在一倍以內，屬于同一梯隊。（5,834,910.0 / 9,291,286.4 ≈ 0.627998，即它能達到 OpenBLAS 62.7998% 的性能）

BlockM4Nv3On512_ikj_M32Parallel算法對于 Single 類型是458.39 GFOPS，Double類型是 215.26 GFOPS。Single的性能是Double的2倍左右（458.39 / 215.26 ≈ 2.1295），這與理論值相同（512位向量能同時計算16個Single，或8個Double）。

5.2 X86 架構 - .NET Framework

從 .NET Framework 4.5開始，開始提供了基本的SIMD硬件加速功能。本程序作了一些兼容處理，使得大部分算法，不用修改源代碼，便能在 .NET Framework 上運行。現在來做一下基準測試。

由于 MKL、OpenBLAS 都是使用自己的動態庫，與 .NET 版本無關。故在測試.NET Framework時，沒必要測試 MKL、OpenBLAS。

當前CPU是 “AMD Ryzen 7 7840H”，操作系統是 “Windows 11”。

5.2.1 Single（單精度浮點型）

X86架構上、.NET Framework 程序、Single類型的基準測試結果如下。

BenchmarkDotNet v0.15.2, Windows 11 (10.0.26100.4946/24H2/2024Update/HudsonValley)
AMD Ryzen 7 7840H w/ Radeon 780M Graphics 3.80GHz, 1 CPU, 16 logical and 8 physical cores
  [Host]    : .NET Framework 4.8.1 (4.8.9310.0), X64 RyuJIT VectorSize=256
  MediumRun : .NET Framework 4.8.1 (4.8.9310.0), X64 RyuJIT VectorSize=256

Method	N	Mean	Error	StdDev	Median	Ratio	RatioSD	Code Size
Basic	1024	4,454,702.840 us	96,843.2650 us	144,950.4510 us	4,487,360.900 us	1.001	0.05	5,687 B
TileRow	1024	966,327.050 us	11,170.0099 us	16,019.6958 us	962,294.050 us	0.217	0.01	1,145 B
TileRowSpan	1024	1,661,727.444 us	16,190.1043 us	22,696.2670 us	1,657,810.200 us	0.373	0.01	1,793 B
TileRowRef	1024	313,248.250 us	4,727.8263 us	6,929.9871 us	310,946.100 us	0.070	0.00	512 B
TileRowSimd	1024	83,757.697 us	5,095.7616 us	7,308.1896 us	81,437.767 us	0.019	0.00	736 B
TileRowSimdFma	1024	90,579.311 us	1,557.4982 us	2,183.3951 us	90,123.900 us	0.020	0.00	746 B
TileRowSimdParallel	1024	11,748.538 us	192.8809 us	288.6951 us	11,706.321 us	0.003	0.00	7,799 B
TileRowSimdFmaParallel	1024	12,838.369 us	227.1818 us	340.0350 us	12,874.963 us	0.003	0.00	7,809 B
BlockM4Nv1_ijk_M32	1024	79,924.653 us	523.0694 us	733.2703 us	79,925.500 us	0.018	0.00	NA
BlockM4Nv1_ijk_M32Parallel	1024	10,929.294 us	317.3551 us	475.0022 us	10,924.080 us	0.002	0.00	NA
BlockM4Nv1_ikj_M32	1024	79,275.543 us	393.1614 us	563.8604 us	79,307.186 us	0.018	0.00	NA
BlockM4Nv1_ikj_M32Parallel	1024	9,784.844 us	304.0108 us	436.0032 us	9,644.648 us	0.002	0.00	NA
BlockM4Nv1_ikj_M4	1024	79,669.252 us	665.6703 us	975.7309 us	79,380.671 us	0.018	0.00	NA
BlockM4Nv1_ikj_M4Parallel	1024	11,542.263 us	193.4875 us	283.6115 us	11,452.883 us	0.003	0.00	NA
BlockM4Nv3_ikj_M4	1024	41,454.059 us	544.8342 us	745.7753 us	41,140.408 us	0.009	0.00	NA
BlockM4Nv3_ikj_M4Parallel	1024	7,906.391 us	427.4508 us	639.7883 us	7,604.690 us	0.002	0.00	NA
BlockM4Nv3_ikj_M32	1024	41,720.557 us	659.2914 us	924.2345 us	41,472.992 us	0.009	0.00	NA
BlockM4Nv3_ikj_M32Parallel	1024	6,674.869 us	290.9010 us	407.8025 us	6,521.323 us	0.002	0.00	NA
UseMathNet	1024	54,745.115 us	783.4180 us	1,172.5833 us	54,466.025 us	0.012	0.00	279 B

測試結果對比如下。

Method	耗時	GFOPS	性能倍數
Basic	4,454,702.840 us	0.45	1.00
TileRow	966,327.050 us	2.07	4.61
TileRowSpan	1,661,727.444 us	1.20	2.68
TileRowRef	313,248.250 us	6.38	14.22
TileRowSimd	83,757.697 us	23.88	53.19
TileRowSimdFma	90,579.311 us	22.08	49.18
TileRowSimdParallel	11,748.538 us	170.23	379.17
TileRowSimdFmaParallel	12,838.369 us	155.78	346.98
BlockM4Nv1_ijk_M32	79,924.653 us	25.02	55.74
BlockM4Nv1_ijk_M32Parallel	10,929.294 us	182.99	407.59
BlockM4Nv1_ikj_M32	79,275.543 us	25.23	56.19
BlockM4Nv1_ikj_M32Parallel	9,784.844 us	204.40	455.27
BlockM4Nv1_ikj_M4	79,669.252 us	25.10	55.91
BlockM4Nv1_ikj_M4Parallel	11,542.263 us	173.28	385.95
BlockM4Nv3_ikj_M4	41,454.059 us	48.25	107.46
BlockM4Nv3_ikj_M4Parallel	7,906.391 us	252.96	563.43
BlockM4Nv3_ikj_M32	41,720.557 us	47.94	106.77
BlockM4Nv3_ikj_M32Parallel	6,674.869 us	299.63	667.38
UseMathNet	54,745.115 us	36.53	81.37

我們表現最好的算法是 BlockM4Nv3_ikj_M32Parallel，它的性能是基礎算法的 667.38 倍，此時的每秒浮點計算次數是 299.63 GFOPS。而 .NET 9.0 是 458.39 GFOPS。.NET Framework 下能達到 65%左右的性能（299.63 / 458.39 ≈ 0.653657），表現已經很不錯了。

還可以注意到，TileRowSpan的性能比較慢。這是因為 .NET Framework 下的Span為了保障兼容性，只能采取性能慢的保守做法。改為托管指針后，能避免這一瓶頸。

5.2.2 Double（雙精度浮點型）

X86架構上、.NET Framework 程序、Double類型的基準測試結果如下。

BenchmarkDotNet v0.15.2, Windows 11 (10.0.26100.4946/24H2/2024Update/HudsonValley)
AMD Ryzen 7 7840H w/ Radeon 780M Graphics 3.80GHz, 1 CPU, 16 logical and 8 physical cores
  [Host]    : .NET Framework 4.8.1 (4.8.9310.0), X64 RyuJIT VectorSize=256
  MediumRun : .NET Framework 4.8.1 (4.8.9310.0), X64 RyuJIT VectorSize=256

Method	N	Mean	Error	StdDev	Median	Ratio	RatioSD	Code Size
Basic	1024	5,219,216.603 us	555,505.4296 us	814,252.7230 us	4,593,251.700 us	1.024	0.22	5,687 B
TileRow	1024	976,825.167 us	8,050.6241 us	11,285.8515 us	973,636.700 us	0.192	0.03	1,145 B
TileRowSpan	1024	1,710,756.415 us	15,104.7271 us	20,675.5227 us	1,712,805.450 us	0.336	0.05	1,793 B
TileRowRef	1024	329,519.486 us	4,073.9472 us	5,842.7338 us	326,634.675 us	0.065	0.01	512 B
TileRowSimd	1024	226,359.507 us	8,571.1670 us	12,292.5126 us	221,183.317 us	0.044	0.01	736 B
TileRowSimdFma	1024	233,129.988 us	9,004.9541 us	12,623.6891 us	230,386.867 us	0.046	0.01	746 B
TileRowSimdParallel	1024	28,560.033 us	251.5022 us	376.4366 us	28,418.494 us	0.006	0.00	7,799 B
TileRowSimdFmaParallel	1024	29,554.618 us	340.4174 us	509.5208 us	29,640.494 us	0.006	0.00	7,809 B
BlockM4Nv1_ijk_M32	1024	162,907.984 us	570.6867 us	781.1624 us	162,883.600 us	0.032	0.00	NA
BlockM4Nv1_ijk_M32Parallel	1024	20,194.872 us	437.9025 us	628.0267 us	19,967.569 us	0.004	0.00	NA
BlockM4Nv1_ikj_M32	1024	162,750.319 us	1,913.2804 us	2,618.9201 us	162,468.392 us	0.032	0.00	NA
BlockM4Nv1_ikj_M32Parallel	1024	19,956.415 us	356.5837 us	533.7177 us	19,780.269 us	0.004	0.00	NA
BlockM4Nv1_ikj_M4	1024	162,956.796 us	783.5110 us	1,018.7856 us	163,084.538 us	0.032	0.00	NA
BlockM4Nv1_ikj_M4Parallel	1024	22,891.121 us	381.4015 us	570.8639 us	22,858.144 us	0.004	0.00	NA
BlockM4Nv3_ikj_M4	1024	83,848.352 us	3,621.1132 us	5,419.9123 us	80,793.929 us	0.016	0.00	NA
BlockM4Nv3_ikj_M4Parallel	1024	15,405.993 us	592.3353 us	886.5797 us	15,284.463 us	0.003	0.00	NA
BlockM4Nv3_ikj_M32	1024	80,101.363 us	2,405.1717 us	3,449.4257 us	79,586.886 us	0.016	0.00	NA
BlockM4Nv3_ikj_M32Parallel	1024	13,063.492 us	528.6187 us	758.1291 us	12,659.439 us	0.003	0.00	NA
UseMathNet	1024	62,791.007 us	962.8950 us	1,411.3992 us	62,336.978 us	0.012	0.00	279 B

測試結果對比如下。

Method	耗時	GFOPS	性能倍數
Basic	5,219,216.603 us	0.38	1.00
TileRow	976,825.167 us	2.05	5.34
TileRowSpan	1,710,756.415 us	1.17	3.05
TileRowRef	329,519.486 us	6.07	15.84
TileRowSimd	226,359.507 us	8.84	23.06
TileRowSimdFma	233,129.988 us	8.58	22.39
TileRowSimdParallel	28,560.033 us	70.03	182.75
TileRowSimdFmaParallel	29,554.618 us	67.67	176.60
BlockM4Nv1_ijk_M32	162,907.984 us	12.28	32.04
BlockM4Nv1_ijk_M32Parallel	20,194.872 us	99.04	258.44
BlockM4Nv1_ikj_M32	162,750.319 us	12.29	32.07
BlockM4Nv1_ikj_M32Parallel	19,956.415 us	100.22	261.53
BlockM4Nv1_ikj_M4	162,956.796 us	12.27	32.03
BlockM4Nv1_ikj_M4Parallel	22,891.121 us	87.37	228.00
BlockM4Nv3_ikj_M4	83,848.352 us	23.85	62.25
BlockM4Nv3_ikj_M4Parallel	15,405.993 us	129.82	338.78
BlockM4Nv3_ikj_M32	80,101.363 us	24.97	65.16
BlockM4Nv3_ikj_M32Parallel	13,063.492 us	153.10	399.53
UseMathNet	62,791.007 us	31.85	83.12

我們表現最好的算法是 BlockM4Nv3_ikj_M32Parallel，它的性能是基礎算法的 399.53 倍，此時的每秒浮點計算次數是 153.10 GFOPS。而 .NET 9.0 是 215.26 GFOPS。.NET Framework 下能達到 71%左右的性能（153.10 / 215.26 ≈ 0.711233），表現已經很不錯了。

5.3 Arm 架構 - .NET 9.0

同樣的源代碼，可以在Arm架構的處理器上運行。

由于 MKL 不支持 Arm架構，且目前nuget上沒有Arm架構的OpenBLAS包，故沒有測試它們。

當前CPU是 “Apple M2”，操作系統是 “macOS Sequoia 15.6.1”。

5.3.1 Single（單精度浮點型）

Arm架構上、.NET 9.0 程序、Single類型的基準測試結果如下。

BenchmarkDotNet v0.15.2, macOS Sequoia 15.6.1 (24G90) [Darwin 24.6.0]
Apple M2, 1 CPU, 8 logical and 8 physical cores
.NET SDK 9.0.102
  [Host]    : .NET 9.0.1 (9.0.124.61010), Arm64 AOT AdvSIMD
  MediumRun : .NET 9.0.1 (9.0.124.61010), Arm64 RyuJIT AdvSIMD

Method	N	Mean	Error	StdDev	Median	Ratio	RatioSD
Basic	1024	3,754,237.106 us	2,074.9078 us	3,041.3732 us	3,753,734.041 us	1.000	0.00
TileRow	1024	840,254.040 us	142.7877 us	200.1684 us	840,254.500 us	0.224	0.00
TileRowSpan	1024	761,125.180 us	498.8317 us	715.4096 us	760,974.583 us	0.203	0.00
TileRowRef	1024	330,818.469 us	106.5126 us	152.7572 us	330,825.885 us	0.088	0.00
TileRowSimd	1024	117,413.868 us	90.4758 us	129.7577 us	117,410.512 us	0.031	0.00
TileRowSimdFmaBcl	1024	117,210.060 us	67.9110 us	99.5431 us	117,214.725 us	0.031	0.00
TileRowSimdFma	1024	117,189.597 us	64.3478 us	94.3201 us	117,187.067 us	0.031	0.00
TileRowSimdParallel	1024	26,510.611 us	185.3270 us	277.3887 us	26,510.653 us	0.007	0.00
TileRowSimdFmaParallel	1024	25,593.386 us	211.9040 us	317.1679 us	25,553.712 us	0.007	0.00
BlockM4Nv1_ijk_M32	1024	152,420.390 us	107.9145 us	161.5213 us	152,420.901 us	0.041	0.00
BlockM4Nv1_ijk_M32Parallel	1024	38,359.750 us	243.9897 us	342.0395 us	38,300.182 us	0.010	0.00
BlockM4Nv1_ikj_M32	1024	148,065.516 us	119.2124 us	178.4315 us	148,031.271 us	0.039	0.00
BlockM4Nv1_ikj_M32Parallel	1024	36,589.371 us	249.5473 us	349.8305 us	36,578.652 us	0.010	0.00
BlockM4Nv1_ikj_M4	1024	146,542.856 us	441.5088 us	647.1579 us	146,317.281 us	0.039	0.00
BlockM4Nv1_ikj_M4Parallel	1024	36,993.328 us	268.5206 us	393.5940 us	37,065.863 us	0.010	0.00
BlockM4Nv3_ikj_M4	1024	489,578.227 us	2,903.1298 us	4,069.7828 us	493,334.646 us	0.130	0.00
BlockM4Nv3_ikj_M4Parallel	1024	17,373.172 us	80.5072 us	115.4610 us	17,399.023 us	0.005	0.00
BlockM4Nv3_ikj_M32	1024	487,247.653 us	1,268.0786 us	1,777.6693 us	488,772.104 us	0.130	0.00
BlockM4Nv3_ikj_M32Parallel	1024	17,908.937 us	119.7722 us	179.2693 us	17,917.776 us	0.005	0.00
BlockM4Nv3On512_ikj_M4	1024	NA	NA	NA	NA	?	?
BlockM4Nv3On512_ikj_M4Parallel	1024	NA	NA	NA	NA	?	?
BlockM4Nv3On512_ikj_M32	1024	NA	NA	NA	NA	?	?
BlockM4Nv3On512_ikj_M32Parallel	1024	NA	NA	NA	NA	?	?
UseMathNet	1024	154,141.940 us	837.3170 us	1,253.2568 us	153,909.807 us	0.041	0.00

測試結果對比如下。

Method	耗時	GFOPS	性能倍數
Basic	3,754,237.106 us	0.53	1.00
TileRow	840,254.040 us	2.38	4.47
TileRowSpan	761,125.180 us	2.63	4.93
TileRowRef	330,818.469 us	6.05	11.35
TileRowSimd	117,413.868 us	17.03	31.97
TileRowSimdFmaBcl	117,210.060 us	17.06	32.03
TileRowSimdFma	117,189.597 us	17.07	32.04
TileRowSimdParallel	26,510.611 us	75.44	141.61
TileRowSimdFmaParallel	25,593.386 us	78.15	146.69
BlockM4Nv1_ijk_M32	152,420.390 us	13.12	24.63
BlockM4Nv1_ijk_M32Parallel	38,359.750 us	52.14	97.87
BlockM4Nv1_ikj_M32	148,065.516 us	13.51	25.36
BlockM4Nv1_ikj_M32Parallel	36,589.371 us	54.66	102.60
BlockM4Nv1_ikj_M4	146,542.856 us	13.65	25.62
BlockM4Nv1_ikj_M4Parallel	36,993.328 us	54.06	101.48
BlockM4Nv3_ikj_M4	489,578.227 us	4.09	7.67
BlockM4Nv3_ikj_M4Parallel	17,373.172 us	115.12	216.09
BlockM4Nv3_ikj_M32	487,247.653 us	4.10	7.70
BlockM4Nv3_ikj_M32Parallel	17,908.937 us	111.68	209.63
UseMathNet	154,141.940 us	12.98	24.36

我們表現最好的算法是 BlockM4Nv3_ikj_M4Parallel，它的性能是基礎算法的 216.09 倍，此時的每秒浮點計算次數是 115.12 GFOPS。

AMD Ryzen 7 7840H 的Single運算速度是458.39 GFOPS。故對于單精度浮點數（Single）的運算，現代CPU均能達到每秒千億次（100GFOPS）級別的運算速度。

Apple M2的向量寬度是128位，而AMD Ryzen 7 7840H 的向量寬度是 512位。假設 Apple M2的向量寬度也達到512位的話，那么理論上會有4倍性能提升，即理論上會是 115.12*4=460.48 GFOPS，這與 AMD Ryzen 7 7840H 的成績非常接近。

5.3.2 Double（雙精度浮點型）

Arm架構上、.NET 9.0 程序、Double類型的基準測試結果如下。

BenchmarkDotNet v0.15.2, macOS Sequoia 15.6.1 (24G90) [Darwin 24.6.0]
Apple M2, 1 CPU, 8 logical and 8 physical cores
.NET SDK 9.0.102
  [Host]    : .NET 9.0.1 (9.0.124.61010), Arm64 AOT AdvSIMD
  MediumRun : .NET 9.0.1 (9.0.124.61010), Arm64 RyuJIT AdvSIMD

Method	N	Mean	Error	StdDev	Median	Ratio	RatioSD
Basic	1024	3,979,217.591 us	3,084.0733 us	4,423.0862 us	3,979,746.459 us	1.000	0.00
TileRow	1024	880,127.965 us	571.4544 us	855.3261 us	880,017.875 us	0.221	0.00
TileRowSpan	1024	797,048.246 us	486.5361 us	713.1583 us	797,011.417 us	0.200	0.00
TileRowRef	1024	348,452.077 us	324.7616 us	465.7634 us	348,371.812 us	0.088	0.00
TileRowSimd	1024	242,866.758 us	231.8556 us	325.0292 us	242,941.903 us	0.061	0.00
TileRowSimdFmaBcl	1024	241,862.247 us	306.1996 us	429.2491 us	241,910.333 us	0.061	0.00
TileRowSimdFma	1024	241,918.592 us	195.5033 us	292.6202 us	241,910.924 us	0.061	0.00
TileRowSimdParallel	1024	57,335.473 us	813.2521 us	1,192.0544 us	57,027.893 us	0.014	0.00
TileRowSimdFmaParallel	1024	55,068.792 us	505.7084 us	741.2608 us	54,973.000 us	0.014	0.00
BlockM4Nv1_ijk_M32	1024	268,039.331 us	388.0223 us	580.7736 us	267,957.021 us	0.067	0.00
BlockM4Nv1_ijk_M32Parallel	1024	65,948.754 us	894.1736 us	1,338.3570 us	66,392.143 us	0.017	0.00
BlockM4Nv1_ikj_M32	1024	265,015.397 us	231.9062 us	332.5930 us	265,013.260 us	0.067	0.00
BlockM4Nv1_ikj_M32Parallel	1024	65,237.383 us	958.7143 us	1,434.9585 us	65,071.180 us	0.016	0.00
BlockM4Nv1_ikj_M4	1024	257,808.595 us	340.6194 us	488.5062 us	257,729.927 us	0.065	0.00
BlockM4Nv1_ikj_M4Parallel	1024	65,421.381 us	691.5592 us	1,013.6786 us	65,436.662 us	0.016	0.00
BlockM4Nv3_ikj_M4	1024	594,005.257 us	137,852.8179 us	206,331.6239 us	694,300.630 us	0.149	0.05
BlockM4Nv3_ikj_M4Parallel	1024	35,414.032 us	584.9320 us	875.4988 us	35,398.204 us	0.009	0.00
BlockM4Nv3_ikj_M32	1024	587,200.067 us	134,524.2102 us	201,349.5203 us	685,058.547 us	0.148	0.05
BlockM4Nv3_ikj_M32Parallel	1024	35,606.024 us	439.7341 us	630.6535 us	35,467.028 us	0.009	0.00
BlockM4Nv3On512_ikj_M4	1024	NA	NA	NA	NA	?	?
BlockM4Nv3On512_ikj_M4Parallel	1024	NA	NA	NA	NA	?	?
BlockM4Nv3On512_ikj_M32	1024	NA	NA	NA	NA	?	?
BlockM4Nv3On512_ikj_M32Parallel	1024	NA	NA	NA	NA	?	?
UseMathNet	1024	172,491.316 us	1,034.3648 us	1,415.8503 us	172,643.514 us	0.043	0.00

測試結果對比如下。

Method	耗時	GFOPS	性能倍數
Basic	3,979,217.591 us	0.50	1.00
TileRow	880,127.965 us	2.27	4.52
TileRowSpan	797,048.246 us	2.51	4.99
TileRowRef	348,452.077 us	5.74	11.42
TileRowSimd	242,866.758 us	8.23	16.38
TileRowSimdFmaBcl	241,862.247 us	8.27	16.45
TileRowSimdFma	241,918.592 us	8.27	16.45
TileRowSimdParallel	57,335.473 us	34.88	69.40
TileRowSimdFmaParallel	55,068.792 us	36.32	72.26
BlockM4Nv1_ijk_M32	268,039.331 us	7.46	14.85
BlockM4Nv1_ijk_M32Parallel	65,948.754 us	30.33	60.34
BlockM4Nv1_ikj_M32	265,015.397 us	7.55	15.02
BlockM4Nv1_ikj_M32Parallel	65,237.383 us	30.66	61.00
BlockM4Nv1_ikj_M4	257,808.595 us	7.76	15.43
BlockM4Nv1_ikj_M4Parallel	65,421.381 us	30.57	60.82
BlockM4Nv3_ikj_M4	594,005.257 us	3.37	6.70
BlockM4Nv3_ikj_M4Parallel	35,414.032 us	56.47	112.36
BlockM4Nv3_ikj_M32	587,200.067 us	3.41	6.78
BlockM4Nv3_ikj_M32Parallel	35,606.024 us	56.17	111.76
UseMathNet	172,491.316 us	11.59	23.07

我們表現最好的算法是 BlockM4Nv3_ikj_M4Parallel，它的性能是基礎算法的 112.36 倍，此時的每秒浮點計算次數是 56.47 GFOPS。

該算法對于 Single 類型是115.12 GFOPS，Double類型是 56.47 GFOPS。Single的性能是Double的2倍左右（115.12 / 56.47 ≈ 2.0386），這與理論值相同。

六、結語

我最開始對 C# 的矩陣乘法程序進行優化時，沒料到能取得這么大的進展。前幾個版本的算法，與采用手動匯編優化等優化技術的MKL、OpenBLAS比起來，性能差距望塵莫及。當時覺得我優化的算法，能超過老牌的 MathNet就很不錯了。

經過不斷改進，性能大幅度提升，最終取得了驚人的成果——不僅單線程成績就能超過并行計算的MathNet，而且并行計算的成績能小幅超過MKL，甚至與OpenBLAS的差距在一倍以內，處于同一梯隊。

即純 C# 編寫的托管代碼程序，與采用了手動匯編優化等優化技術的專業矩陣運算庫，達到同一梯隊的性能水平。

首先，這得益于 .NET 9.0 生成的匯編代碼的質量比較高。例如 .NET Framework 生成的匯編代碼就差一些，性能只有 .NET 9.0 的 60%左右。

其次，雖然.NET 9.0 生成的匯編代碼質量比較高，但比起MKL、OpenBLAS里手工優化的匯編代碼，各方面還是差了不少。但得益于現代 CPU的解碼、亂序執行、分支預測等功能的日益強大，即使面對質量稍差匯編代碼，CPU也會盡可能高效地運算。

其實矩陣乘法程序還有很大的優化空間，例如使用各種CPU架構的矩陣運算加速專用指令、為各種矩陣尺寸找出最佳的分塊尺寸等。現在OpenBLAS在很多場合超過 MKL，就是因為這些原因。

希望我的文章能給讀者們帶來啟發。

附錄

源代碼地址: https://github.com/zyl910/MatrixBenchmarkCs/tree/v0.1
【深緩中字】為什么6層嵌套循環讓這個算法快了120倍？
矩陣乘法優化過程（DGEMM）
關于sgemm_hsw的一點解釋說明
通用矩陣乘法（GEMM）原理實現與優化方法總覽
OpenBLAS項目與矩陣乘法優化 | AI 研習社
OpenBLAS
Intel? oneAPI Math Kernel Library (oneMKL)
C# 使用SIMD向量類型加速浮點數組求和運算（1）：使用Vector4、Vector<T>
C# 使用SIMD向量類型加速浮點數組求和運算（4）：用引用代替指針, 擺脫unsafe關鍵字，兼談Unsafe類的使用

posted on 2025-08-31 17:35 zyl910 閱讀(229) 評論(3) 收藏舉報

刷新頁面返回頂部

zyl910

公告

一、基本算法與測試辦法

1.1 矩陣乘法的定義

1.1.1 矩陣形狀與運算復雜度

1.2 C++ 開發的矩陣乘法最基礎實現

1.3 C# 開發的矩陣乘法最基礎實現（Basic）

1.3.1 矩陣乘法的實現

1.3.2 基準測試方法

1.4 增加MathNet、MKL、OpenBLAS的基準測試

1.4.1 引入庫

1.4.2 這些庫的基準測試方法

1.4.2.1 MathNet的基準測試方法（UseMathNet）

1.4.2.2 OpenBLAS的基準測試方法（UseOpenBLAS）

1.4.2.3 MKL的基準測試方法（UseMKL）

1.4.3 目前的基準測試結果

二、標量算法優化

2.1 循環順序由ijk改為ikj（TileRow）

2.1.1 算法的實現

2.1.1.1 矩陣清零

2.1.2 基準測試方法

2.1.3 基準測試結果

2.2 性能為什么會有這么大提升呢？

2.2.1 循環次序ijk（Basic）

2.2.2 循環次序ikj（TileRow）

2.3 使用Span及消除索引計算時的乘法開銷（TileRowSpan）

2.3.1 算法的實現

2.3.2 基準測試方法

2.3.3 基準測試結果

2.4 使用托管指針進一步降低地址計算的開銷（TileRowRef）

2.4.1 算法的實現

2.4.1.1 矩陣清零

2.4.2 基準測試方法

2.4.3 基準測試結果

三、向量算法優化與并行加速

3.1 使用SIMD硬件加速技術的向量算法（TileRowSimd）

3.1.1 算法的實現

3.1.2 基準測試方法

3.1.3 基準測試結果

3.2 基于TileRowSimd的并行加速（TileRowSimdParallel）

3.2.1 基準測試方法

3.2.2 基準測試結果

3.3 使用FusedMultiplyAdd（TileRowSimdFmaBcl）

3.1.1 算法的實現

3.1.2 基準測試方法

3.1.3 基準測試結果

3.1.4 加上TileRowSimdFmaX86的測試

3.1.4.1 TileRowSimdFmaX86的測試結果

3.4 將乘加運算封裝為函數且測試并行加速（TileRowSimdFma、TileRowSimdFmaParallel）

3.4.1 乘加運算封裝為函數

3.4.2 矩陣乘法的代碼

3.4.3 基準測試方法

3.4.4 基準測試結果

四、矩陣分塊優化

4.1 4行、1倍向量寬度、ijk順序的分塊算法（BlockM4Nv1_ijk_M32、BlockM4Nv1_ijk_M32Parallel）

4.1.1 公共方法的改進

4.1.2 矩陣乘法內核算法

4.1.3 矩陣乘法完整算法

4.1.4 基準測試方法

4.1.5 基準測試結果

4.2 4行、1倍向量寬度、ikj順序的分塊算法（BlockM4Nv1_ikj_M32、BlockM4Nv1_ikj_M32Parallel、BlockM4Nv1_ikj_M4、BlockM4Nv1_ikj_M4Parallel）

4.2.1 矩陣乘法內核算法

4.2.2 矩陣乘法完整算法

4.2.3 基準測試方法

4.2.4 基準測試結果

4.3 4行、3倍向量寬度、ijk順序的分塊算法（BlockM4Nv3_ikj_M32、BlockM4Nv3_ikj_M32Parallel、BlockM4Nv3_ikj_M4、BlockM4Nv3_ikj_M4Parallel）

4.3.1 公共方法的改進

4.3.2 矩陣乘法內核算法

4.3.3 矩陣乘法完整算法

4.3.4 基準測試方法

4.3.5 基準測試結果

4.4 4行、3倍512位向量寬度、ijk順序的分塊算法（BlockM4Nv3On512_ikj_M32、BlockM4Nv3On512_ikj_M32Parallel、BlockM4Nv3On512_ikj_M4、BlockM4Nv3On512_ikj_M4Parallel）

4.4.1 公共方法的改進

4.4.2 矩陣乘法內核算法

4.4.3 矩陣乘法完整算法

4.4.4 基準測試方法

4.4.5 基準測試結果

五、基準測試結果

5.1 X86 架構 - .NET 9.0

5.1.1 Single（單精度浮點型）

4.1 4行、1倍向量寬度、ijk順序的分塊算法（`BlockM4Nv1_ijk_M32`、`BlockM4Nv1_ijk_M32Parallel`）

4.2 4行、1倍向量寬度、ikj順序的分塊算法（`BlockM4Nv1_ikj_M32`、`BlockM4Nv1_ikj_M32Parallel`、`BlockM4Nv1_ikj_M4`、`BlockM4Nv1_ikj_M4Parallel`）

4.3 4行、3倍向量寬度、ijk順序的分塊算法（`BlockM4Nv3_ikj_M32`、`BlockM4Nv3_ikj_M32Parallel`、`BlockM4Nv3_ikj_M4`、`BlockM4Nv3_ikj_M4Parallel`）

4.4 4行、3倍512位向量寬度、ijk順序的分塊算法（`BlockM4Nv3On512_ikj_M32`、`BlockM4Nv3On512_ikj_M32Parallel`、`BlockM4Nv3On512_ikj_M4`、`BlockM4Nv3On512_ikj_M4Parallel`）