- [1] 前言
- [2] 設(shè)計(jì)與分析
- [3] 采坑心得
- [4] 改進(jìn)建議
- [5] 總結(jié)
- (1)前言
本篇文章總體分析PTA中題目集5-題目集7:
<1> 題目集5總共5道題目,前四道均為簡(jiǎn)單題,主要考察對(duì)正則表達(dá)式基礎(chǔ)的應(yīng)用,而第五道為算法復(fù)雜的電梯調(diào)度程序;
<2> 題目集6總共3道題,前兩道為算法簡(jiǎn)單的面向?qū)ο箢愒O(shè)計(jì)題,第三道為題目集5電梯調(diào)度程序的重構(gòu)和模塊化設(shè)計(jì),必須符合單一職責(zé)原則(SRP);
<3> 題目集7總共3道題,前兩道為算法簡(jiǎn)單的類設(shè)計(jì)題,第三道為題目集6電梯調(diào)度程序的二次迭代。
- (2)設(shè)計(jì)與分析
1.題目集5電梯單部調(diào)度問題:
SouceMonitor分析圖:

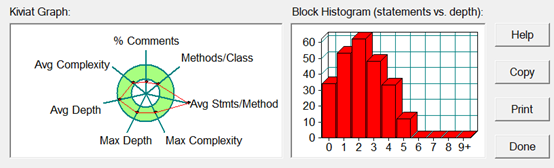
解釋:
根據(jù)左邊的Kiviat圖和上面準(zhǔn)確的Value值可知:每個(gè)方法的平均語句數(shù)Avg Stmts/Method(23.56)遠(yuǎn)超綠色范圍的正常值,說明存在代碼堆積,過度嵌套多重if-else語句。實(shí)際上確實(shí)如此,第一次的電梯算法中還停留在面向過程的解題思維中,源碼中總共也就兩個(gè)類(elevator和Main),許多方法全部堆砌在elevator類中,缺乏模塊化思維。
心得:
合理分析不同算法邏輯的實(shí)現(xiàn)過程,盡量把類里的每個(gè)方法各自獨(dú)立實(shí)現(xiàn)自己的特有功能,把不同的功能放在不同的方法中代碼可讀性也強(qiáng),對(duì)代碼改進(jìn)和優(yōu)化時(shí)也輕松。
2. 題目集6電梯單部調(diào)度問題:
類圖:

SouceMonitor分析圖:


解釋:
根據(jù)左邊的Kiviat圖和上面準(zhǔn)確的Value值可知:對(duì)比上次的題目集5的電梯算法,這次的每個(gè)方法的平均語句數(shù)Avg Stmts/Method(8.35)處于綠色范圍的正常值,說明不存在代碼過度堆積問題。但最大圈復(fù)雜度Max Complexity(11)超過正常值,存在過度嵌套多重if-else語句。分析源代碼中,確實(shí)有兩個(gè)方法getMaxFloor()和getMinFloor(),在分析電梯上行和下行過程中,使用多個(gè)if-else語句判斷樓層和方向。此外我的最終源代碼500行遠(yuǎn)超過PTA的代碼限度,無法正常提交代碼,說明存在許多冗余和無效的代碼量,或者類的設(shè)計(jì)不規(guī)范,不高效,后續(xù)需要進(jìn)一步改進(jìn)與優(yōu)化。
心得:
面對(duì)過于復(fù)雜的算法和邏輯,不宜過多使用if-else語句,后續(xù)需要進(jìn)一步學(xué)習(xí),用面向?qū)ο?/strong>的思維重構(gòu)代碼。
3. 題目集7電梯單部調(diào)度問題:
SouceMonitor分析圖:
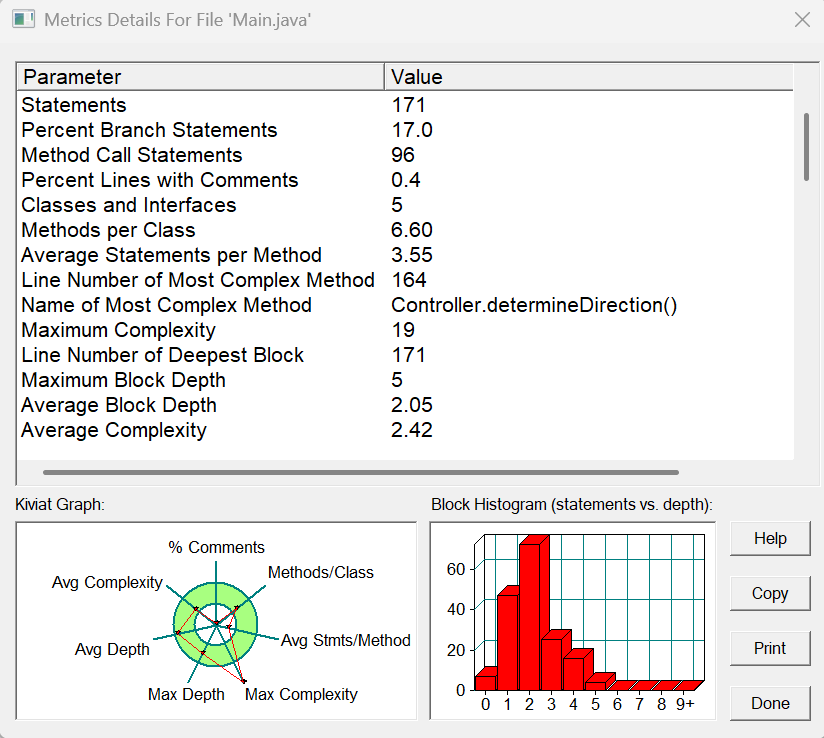
解釋
題目集7目前的電梯程序只實(shí)現(xiàn)了部分測(cè)試數(shù)據(jù)和算法邏輯,對(duì)于當(dāng)前的源碼進(jìn)行分析可知:
最大圈復(fù)雜度Max Complexity遠(yuǎn)超過正常值,后續(xù)仍需要對(duì)源碼進(jìn)行合理優(yōu)化與重構(gòu)。
- (3)采坑心得
1.前部分題目心得
提交的錯(cuò)誤源碼:
點(diǎn)擊查看代碼
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
String input = scanner.nextLine();
if(input.length() <= 4 || input.length() >= 16) {
System.out.print("你輸入的QQ號(hào)驗(yàn)證失敗");
return;
}
if(input.matches("[1-9][\\d]")) {
System.out.print("你輸入的QQ號(hào)驗(yàn)證成功");
}else {
System.out.print("你輸入的QQ號(hào)驗(yàn)證失敗");
}
}
}
(2)不熟練正則表達(dá)式的使用,長(zhǎng)度校驗(yàn)和數(shù)字校驗(yàn)均可隱藏在正則中,
首字符非0 ?[1-9]
全數(shù)字校驗(yàn)和長(zhǎng)度校驗(yàn) ?\d{4,1}
(3)隨機(jī)計(jì)數(shù)的點(diǎn)分布在內(nèi)接圓中為整形(int hits),返回ruturn時(shí)準(zhǔn)確值不夠精確,丟失了部分小數(shù)點(diǎn)后的精確值,導(dǎo)致與π的差值較大。因此需要強(qiáng)制轉(zhuǎn)換會(huì)double類型。
強(qiáng)制轉(zhuǎn)換類型的代碼:
點(diǎn)擊查看代碼
public double simulation(int n) {
int hits = 0;
for(int i = 0;i < n;i++) {
double x = rectangle.coordinate.getAbscissa() + Math.random() * rectangle.getLength();
double y = rectangle.coordinate.getOrdinate() - Math.random() * rectangle.getWidth();
Coordinate randomcoordinate = new Coordinate(x,y);
if(getDistance(circle.getCoordinate(),randomcoordinate) <= circle.getRadius()) {
hits++;
}
}
return (double)(4 * hits) / n;//強(qiáng)制int轉(zhuǎn)換為double
}
2. 單部電梯調(diào)度問題:
提交的問題:


采坑心得體會(huì):
在不斷改進(jìn)和提交源碼的過程中,前部分源碼提交過程大部分出現(xiàn)的問題為運(yùn)行超時(shí),說明算法實(shí)現(xiàn)的邏輯不完整,有漏洞導(dǎo)致死循環(huán),需要改正和調(diào)整正確邏輯和算法;
后部分源碼提交過程出現(xiàn)的問題幾乎全是答案錯(cuò)誤,說明邏輯實(shí)現(xiàn)了閉環(huán),但源碼算法實(shí)現(xiàn)的過程與測(cè)試點(diǎn)實(shí)現(xiàn)的需求不符合,需要更改錯(cuò)誤實(shí)現(xiàn)的邏輯和算法。
- (4)改進(jìn)建議
-
電梯多類設(shè)計(jì)仍然存在不合理和不規(guī)范的情況:代碼集中在Controlle類
(包含addIntenalRequest,addExternalRequest,processRequests,getMaxUpFloor,getMinDownFloor,handleRequestsAtCurrentFloor等方法)中;
其中的addIntenalRequest和addExternalRequest方法應(yīng)該放在RequestsQueue類中才合理,后續(xù)應(yīng)該對(duì)相應(yīng)代碼改進(jìn)與優(yōu)化。 -
電梯類算法設(shè)計(jì)冗長(zhǎng),有一些邏輯可以合并一起處理;
例如如下getMaxUpFloor()方法:
點(diǎn)擊查看代碼
private TargetFloor getMaxUpFloor() {
// 定義候選變量
Integer insideCandidate = null;
Integer outsideCandidate = null;
int currentFloor = elevator.getCurrentFloor();
LinkedList<Integer> outsideUpRequests = queue.getExternalUpRequests();
LinkedList<Integer> outsideDownRequests = queue.getExternalDownRequests();
if (!queue.getInternalRequests().isEmpty() && queue.getInternalRequests().peek() >= currentFloor) {
insideCandidate = queue.getInternalRequests().peek();
}
if (!queue.getExternalRequests().isEmpty() && queue.getExternalRequests().peek() >= currentFloor) {
outsideCandidate = queue.getExternalRequests().peek();
}
if (queue.getInternalRequests().isEmpty()) {
if (queue.getExternalRequests().isEmpty()) {
return null;
}
else if(!queue.getExternalRequests().isEmpty()) {
if(queue.getExternalRequests().peek() == outsideDownRequests.peek()) {
return new TargetFloor(queue.getExternalRequests().peek(), "DOWN");
}
else if(queue.getExternalRequests().peek() == outsideUpRequests.peek()) {
return new TargetFloor(queue.getExternalRequests().peek(), "UP");
}
}
}
else if(!queue.getInternalRequests().isEmpty() && insideCandidate == null) {//內(nèi)部無效
if(queue.getExternalRequests().isEmpty()) {
return new TargetFloor(queue.getInternalRequests().peek(), "DOWN");
}
else if(outsideCandidate != null) {
if(queue.getExternalRequests().peek() == outsideUpRequests.peek()) {
return new TargetFloor(queue.getExternalRequests().peek(), "UP");
}
else if(queue.getExternalRequests().peek() == outsideDownRequests.peek() && queue.getExternalRequests().peek() < outsideDownRequests.peek()) {
return new TargetFloor(queue.getExternalRequests().peek(), "DOWN");
}
else if(queue.getExternalRequests().peek() == outsideDownRequests.peek() && queue.getExternalRequests().peek() > outsideDownRequests.peek()) {
return new TargetFloor(queue.getExternalRequests().peek(), "UP");
}
}
else if(outsideCandidate == null) {//外部無效
if(queue.getInternalRequests().peek() > queue.getExternalRequests().peek()) {
return new TargetFloor(queue.getInternalRequests().peek(), "DOWN");
}
else if(queue.getInternalRequests().peek() == queue.getExternalRequests().peek()) {
if(queue.getExternalRequests().peek() == outsideDownRequests.peek()) {
return new TargetFloor(queue.getExternalRequests().peek(), "DOWN");
}
else if(queue.getExternalRequests().peek() == outsideUpRequests.peek()) {
return new TargetFloor(queue.getExternalRequests().peek(), "DOWN");
}
}
else if(queue.getInternalRequests().peek() < queue.getExternalRequests().peek()) {
if(queue.getExternalRequests().peek() == outsideUpRequests.peek()) {
return new TargetFloor(queue.getInternalRequests().peek(), "DOWN");
}
else if(queue.getExternalRequests().peek() == outsideDownRequests.peek()) {
return new TargetFloor(queue.getExternalRequests().peek(), "DOWN");
}
}
}
}
else if(insideCandidate != null) {
if(queue.getExternalRequests().peek() == null) {
return new TargetFloor(queue.getInternalRequests().peek(), "UP");
}
else if(outsideCandidate == null) {//外部無效
return new TargetFloor(queue.getInternalRequests().peek(), "UP");
}
else if(queue.getInternalRequests().peek() < queue.getExternalRequests().peek()) {
return new TargetFloor(queue.getInternalRequests().peek(), "UP");
}
else if(queue.getInternalRequests().peek() == queue.getExternalRequests().peek()) {
if(queue.getExternalRequests().peek() == outsideUpRequests.peek()) {
return new TargetFloor(queue.getExternalRequests().peek(), "UP");
}
else if(queue.getExternalRequests().peek() == outsideDownRequests.peek()) {
return new TargetFloor(queue.getExternalRequests().peek(), "UP");
}
}
else if(queue.getInternalRequests().peek() > queue.getExternalRequests().peek()) {
if(queue.getExternalRequests().peek() == outsideUpRequests.peek()) {
return new TargetFloor(queue.getExternalRequests().peek(), "UP");
}
else if(queue.getExternalRequests().peek() == outsideDownRequests.peek()) {
return new TargetFloor(queue.getInternalRequests().peek(), "UP");
}
}
}
return null;
}
其它的像getMinDownFloor()方法與上部分方法類似,均可以優(yōu)化處理不必要和無效的代碼量。
- (5)總結(jié)
-
通過3周的Java題目集訓(xùn)練,我基本上能理解和實(shí)現(xiàn)簡(jiǎn)單的Java面向?qū)ο缶幊蹋斫饬祟惻c對(duì)象的封裝特性,初步掌握了基本的模塊化設(shè)計(jì)的實(shí)現(xiàn)方法。
例如,通過電梯調(diào)度系統(tǒng)的開發(fā),實(shí)踐了將復(fù)雜功能拆解為獨(dú)立對(duì)象(如電梯本體、請(qǐng)求隊(duì)列、調(diào)度器)的工程化思維,初步了解了代碼結(jié)構(gòu)化設(shè)計(jì)模式。 -
在面對(duì)復(fù)雜的算法邏輯題時(shí),沒有認(rèn)真分析題目,找到最佳的算法思路,導(dǎo)致浪費(fèi)很多時(shí)間,效率低。
例如:在寫題目集5電梯類時(shí),一開始就直接分析三個(gè)隊(duì)列的不同組合情況(內(nèi)部需求,外部向上需求,外部向下需求),不但草稿演算浪費(fèi)5,6張紙,最后運(yùn)行調(diào)試后發(fā)現(xiàn)電梯算法(與后續(xù)新增的測(cè)試樣例)部分電梯運(yùn)行過程是錯(cuò)的;最后發(fā)現(xiàn)分析兩個(gè)隊(duì)列(內(nèi)部需求,外部需求)僅可,而(向上和向下)只需要判斷一下方向即可。 -
目前的有關(guān)類設(shè)計(jì)的題目,課程組老師均給出了類圖,對(duì)應(yīng)著類圖編程相對(duì)比較輕松。只需要思考每個(gè)類里的方法算法邏輯如何實(shí)現(xiàn)的即可。如果不看對(duì)應(yīng)的類圖直接寫代碼,我目前對(duì)面向?qū)ο缶幊痰乃悸窌?huì)不清晰,沒有邏輯,又會(huì)回到面向過程的編程中去;因此,在后續(xù)的學(xué)習(xí)中,需要進(jìn)一步培養(yǎng)分析對(duì)象和類設(shè)計(jì)的能力,更好的適應(yīng)面向?qū)ο缶幊獭?/p>



 浙公網(wǎng)安備 33010602011771號(hào)
浙公網(wǎng)安備 33010602011771號(hào)