最長(zhǎng)公共子序列圖解、算法實(shí)現(xiàn)和復(fù)雜度分析
LCS和萊文斯坦距離的解決思路非常類(lèi)似,都是利用動(dòng)態(tài)規(guī)劃的方式來(lái)解決。可以參見(jiàn)上一篇“萊文斯坦距離”,兩個(gè)概念對(duì)比著看理解為更深入!
LCS定義
同樣引用百科:
最長(zhǎng)公共子序列(LCS)是一個(gè)在一個(gè)序列集合中(通常為兩個(gè)序列)用來(lái)查找所有序列中最長(zhǎng)子序列的問(wèn)題。與查找最長(zhǎng)公共子串的問(wèn)題不同的地方是:子序列不需要在原序列中占用連續(xù)的位置。最長(zhǎng)公共子序列問(wèn)題是一個(gè)經(jīng)典的計(jì)算機(jī)科學(xué)問(wèn)題,也是數(shù)據(jù)比較程序,比如Diff工具,和生物信息學(xué)應(yīng)用的基礎(chǔ)。它也被廣泛地應(yīng)用在版本控制,比如Git用來(lái)調(diào)和文件之間的改變。
狀態(tài)轉(zhuǎn)移方程
如果產(chǎn)出的是最長(zhǎng)公共子序列的長(zhǎng)度,則方程為:
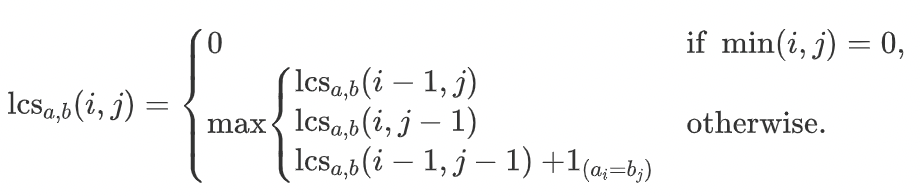
注意:上面狀態(tài)轉(zhuǎn)移方程中,最后的1是一個(gè)指示函數(shù),表示如果a字符串第i個(gè)字符和b字符串第j個(gè)字符相同則為1,否則取0;
如果最終需要產(chǎn)出最長(zhǎng)公共子序列的具體內(nèi)容,則可以在動(dòng)態(tài)規(guī)劃的每一步驟保存當(dāng)前LCS字符串,則最后一步產(chǎn)出的就是兩個(gè)輸入字符串的LCS。對(duì)應(yīng)的狀態(tài)轉(zhuǎn)移方程也要適當(dāng)變一下:
1. min(i, j) == 0時(shí),lcs的取值從0改為空字符串;
2. 最后一行指示函數(shù)的值從1改為ai字符的內(nèi)容。如下所示:
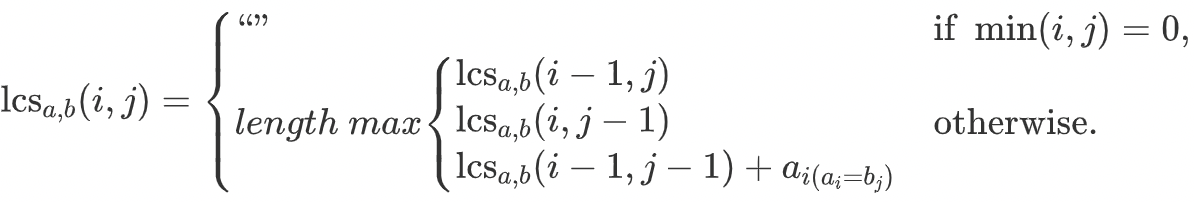
計(jì)算過(guò)程圖解
假設(shè)要計(jì)算str_a = "abcdd" 和 str_b = "aacbd" 的最長(zhǎng)公共子序列,則可以橫向從左向右遍歷(方便起見(jiàn),單元格里記錄的是lcs的長(zhǎng)度,放lcs字符串的話(huà)寫(xiě)不下。。):

如圖所示,按照狀態(tài)轉(zhuǎn)移方程,除了第一行和第一列之外的每個(gè)單元格,都只依賴(lài)其左、上、左上三個(gè)單元格的內(nèi)容,所以每一行的計(jì)算只需要緩存當(dāng)前橫行和上一橫行的內(nèi)容即可。
代碼實(shí)現(xiàn)
python實(shí)現(xiàn)代碼如下:

1 #-*- encoding:utf-8 -*- 2 import sys 3 import pdb 4 5 6 def lcs(str_a, str_b): 7 """最長(zhǎng)公共子序列 8 attributes: 9 str_a: 字符串a(chǎn) 10 str_b: 字符串b 11 return: 12 兩個(gè)字符串的最長(zhǎng)公共子序列內(nèi)容 13 exception: 14 TypeError 15 """ 16 17 # 異常檢測(cè) 18 if not isinstance(str_a, basestring) or not isinstance(str_b, basestring): 19 raise TypeError("Input must be string!") 20 21 # 定義lcs記錄矩陣 22 matrix = [["" for j in range(len(str_b) + 1)] for i in range(len(str_a) + 1)] 23 24 for i in range(1, len(str_a) + 1): 25 for j in range(1, len(str_b) + 1): 26 sub_a = matrix[i - 1][j] # 上方單元格 27 sub_b = matrix[i][j - 1] # 左側(cè)單元格 28 sub_a_b = matrix[i - 1][j - 1] \ 29 + (str_a[i - 1] if str_a[i - 1] == str_b[j - 1] else "") # 左上單元格 30 31 # 記錄下最長(zhǎng)的字符串 32 tmp_str = sub_a if len(sub_a) > len(sub_b) else sub_b 33 matrix[i][j] = tmp_str if len(tmp_str) > len(sub_a_b) else sub_a_b 34 35 return matrix[-1][-1] 36 37 38 def main(str_a, str_b): 39 ret = lcs(str_a, str_b) 40 print("lcs=%s, lcs_length=%s" % (ret, len(ret))) 41 42 43 if __name__ == '__main__': 44 main(sys.argv[1], sys.argv[2])
執(zhí)行結(jié)果
[work@yq01-kg-saa-dev-general0.yq01.baidu.com longest_common_subsequence]$ python lcs_dp.py abcde acdebbbbbb
lcs=acde, lcs_length=4
空間復(fù)雜度優(yōu)化后的代碼。優(yōu)化點(diǎn)有兩個(gè):
1. 只創(chuàng)建一個(gè)2行的記錄矩陣,節(jié)省空間;
2. 記錄矩陣的列選取相對(duì)短的字符串的長(zhǎng)度

1 #-*- encoding:utf-8 -*- 2 import sys 3 import pdb 4 5 6 def lcs(str_a, str_b): 7 """最長(zhǎng)公共子序列 8 attributes: 9 str_a: 字符串a(chǎn) 10 str_b: 字符串b 11 return: 12 兩個(gè)字符串的最長(zhǎng)公共子序列內(nèi)容 13 exception: 14 TypeError: 輸入的不是字符串 15 """ 16 17 # 異常檢測(cè) 18 if not isinstance(str_a, basestring) or not isinstance(str_b, basestring): 19 raise TypeError("Input must be string!") 20 21 # 讓str_b為更短的字符串,這樣空間復(fù)雜度能更小一些 22 if len(str_a) < len(str_b): 23 tmp = str_b 24 str_b = str_a 25 str_a = tmp 26 27 # 定義一個(gè)2 * (len(str_b)+1)的記錄矩陣 28 matrix = [["" for j in range(len(str_b) + 1)] for i in range(2)] 29 curr_i = 1 30 31 for i in range(1, len(str_a) + 1): 32 for j in range(1, len(str_b) + 1): 33 sub_a = matrix[1 - curr_i][j] 34 sub_b = matrix[curr_i][j - 1] 35 sub_a_b = matrix[1 - curr_i][j - 1] \ 36 + (str_a[i - 1] if str_a[i - 1] == str_b[j - 1] else "") 37 38 # 記錄下最長(zhǎng)的字符串 39 tmp_str = sub_a if len(sub_a) > len(sub_b) else sub_b 40 matrix[curr_i][j] = tmp_str if len(tmp_str) > len(sub_a_b) else sub_a_b 41 curr_i = 1 - curr_i 42 43 return matrix[1 - curr_i][-1] 44 45 46 def main(str_a, str_b): 47 ret = lcs(str_a, str_b) 48 print("lcs=%s, lcs_length=%s" % (ret, len(ret))) 49 50 51 if __name__ == '__main__': 52 main(sys.argv[1], sys.argv[2])
執(zhí)行結(jié)果
$ python lcs_dp_opt.py abcde acdeb
lcs=acde, lcs_length=4
復(fù)雜度分析
類(lèi)比萊文斯坦距離的復(fù)雜度:
1. LCS的時(shí)間復(fù)雜度是O(m * n)
2. LCS的空間復(fù)雜度也是O(m * n),但同樣也可以?xún)?yōu)化成O(2 * min(m, n)),即可以達(dá)到O(n)級(jí)別





 浙公網(wǎng)安備 33010602011771號(hào)
浙公網(wǎng)安備 33010602011771號(hào)