探索性數據分析（Exploratory Data Analysis）

本節課程先從統計分析四步驟中的第二步：EDA開始。

課程定義了若干個術語，如果學習過機器學習的同學，應該很容易類比理解：

• population：上節課說過，整體數據集合被稱作population
• individual：其中每個個體，課程里稱之為individual，注意不僅僅指個人，也可以泛指其他集合的其中一條數據
• variable：變量，即描述個體的某個特點，類比機器學習中的特征
• dataset：從population中圈定的一個子集

舉個例子：

這是一個用藥記錄表，其中每一行是一個individual，每一列是一個variable

變量的類型

variable可以細分為兩種：Categorical variables 分類變量（也叫Qualitative variables 定性變量）和 Quantitative variables 定量變量

前者一般就是指離散型變量，后者一般指連續型變量。

課程中還提到另一種變量（或叫特征）的分類方法：

• Nominal variable：名義變量（也叫定類變量），是最不精確的度量方法，只能用來區分差別（difference）。例如生物類別：狗、貓、牛、馬、人、細菌……就是典型的名義變量。其特點是：各個值之間沒有優劣之分，是平等的，自然也無法相互比較和計算。
• Ordinal variable：序數變量，其比Nominal variable精確一些，其可以對不同值進行排序。例如比賽的名次：冠軍、亞軍、季軍、第四名……就是典型的有序變量。這類變量的特點是：各個值之間有順序或者說優劣（如冠軍最好，亞軍次之，最后一名最差等），但是彼此之間的間隔既不固定也不相等（如跳水冠軍123分、亞軍96分、季軍95分）。
• Interval variable：區間變量，其比序數變量更精確一些，其相鄰的值之間的差異是固定或者說相等的。例如溫度計：100攝氏度和99攝氏度、99攝氏度和98攝氏度之間都相差1個攝氏度，可以看到這個差值是固定的，或者說相鄰的兩個值之間的差是相等的。但區間變量中的0不能表示“沒有”這種變量或特征，比如0攝氏度，其并不代表沒有溫度了（因為0度是有意義的，此外還有零下20度、零下100度等）。【個人理解：就是interval variable的特征是可以取0值的，或者說0值是有效的值】
• Ratio：比例/比率。是最精確的度量方法，其比區間變量更精確，與區間變量的差別也就是其中的0可以表示沒有這種變量或特征。比如年齡：0歲就表示沒有年齡；身高：0cm表示沒有身高；體重：0kg表示沒有體重；【個人理解：就是ratio的0值表示的是這一條individual在這個特征上是缺失的，即沒有有效值，但ratio的0是否可以用于分析呢？這個需要繼續往下學習了……】

注意上述四個度量方法之間，能夠用高精度的方法度量的變量，也可以轉為用低精度的方法來度量，比如年齡是ratio，其可以轉為用ordinal variable來度量（比如嬰兒期、幼兒期、青年、中年、老年等）；但反之不行，比如冠軍和亞軍之間無法用interval variable或ratio來度量。

interval variable 和 ratio之間可能比較難區分，多看一些例子可能會好一些：

1. 考試分數是哪種？答案是interval variable，因為0分是可以存在的，考試可以考0分，而不能說成0分表示根本沒參加考試；
2. 老師在課堂上留給學生討論的分鐘數是哪種？答案是ratio，因為0表示老師根本沒留時間給學生討論，而一般不能說成“老師留了0分鐘給學生討論”；

有sense了嗎？interval variable的0表示事情發生了其結果是0（或可以發生結果是0的事情）；而ratio的0表示事情根本沒發生（或根本不存在）。

單個變量的分析

從這里開始，課程闡述了EDA在做什么——可以理解為觀察變量自身的特點、變量之間的關系、變量與結果之間的關系。

所以先從單個變量開始，即只看一個變量自身的特點分析。

單個變量的圖示方法

單個分類變量（Categorical variables）一般可以用餅狀圖（pie chart)表示：

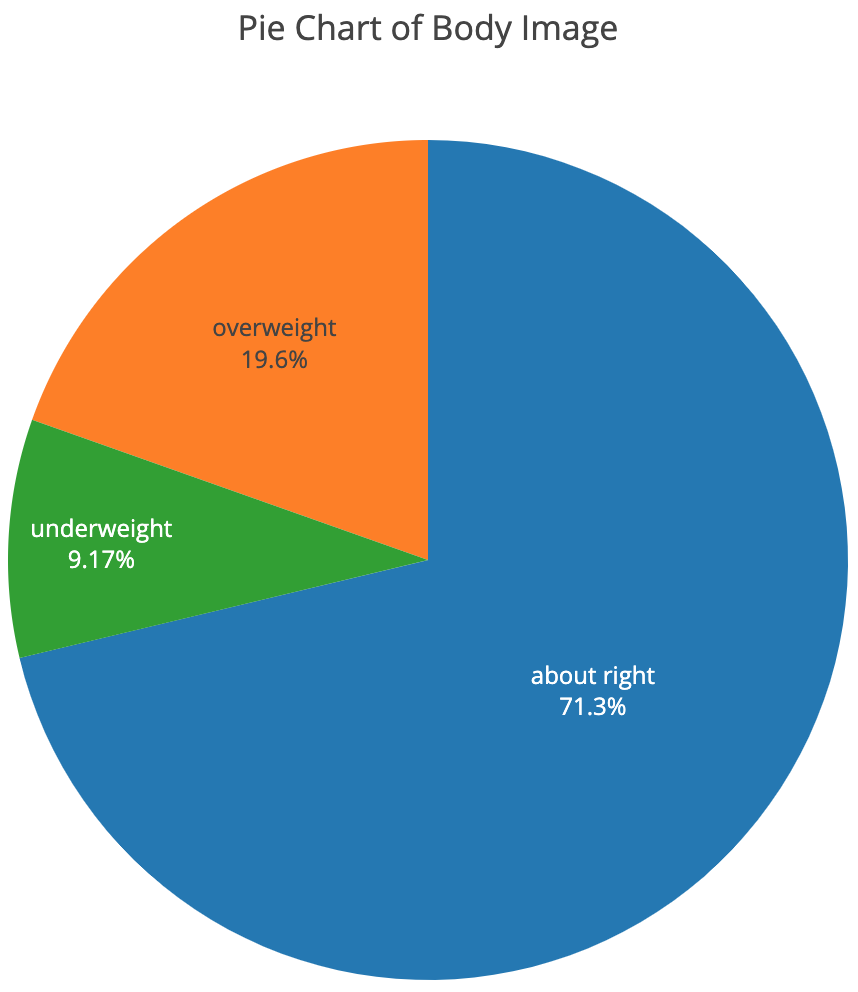
餅狀圖一般適合表示變量的每種取值與全局的關系。

也可以用柱狀圖(bar chart)來表示：

柱狀圖一般適合表示變量的每種取值之間的對比（柱狀圖Y軸的值可以從值value改為百分比percent）。

單個定量變量（Quantitative variables）一般用直方圖(histogram)：

莖葉圖(stemplot)：

或箱線圖(boxplot)表示。

下一篇就從直方圖開始詳細介紹對于單個連續性變量的EDA分析，包括各種術語、概念的方法論。