1.本周學習總結

1.思維導圖

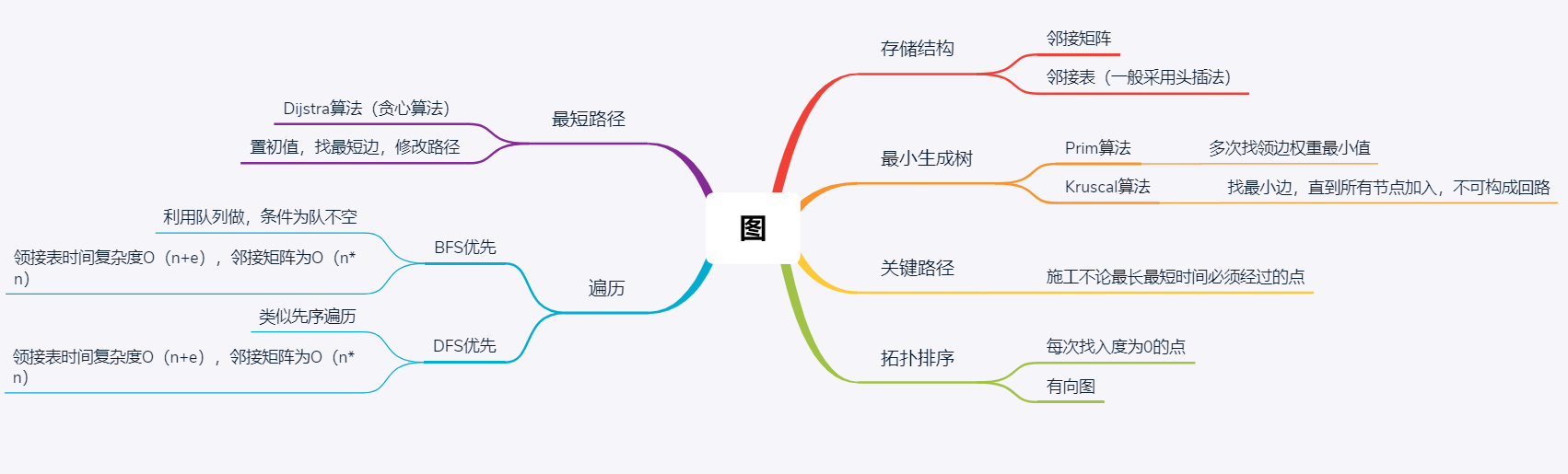
2.談談你對圖結構的認識及學習體會

對圖結構的學習，發現容器超好用，他大大減少了代碼量，庫函數的調用非常方便。下面是總結的一些常用庫函數

1.vector類常用的函數

• vector():創建一個空vector
• vector(begin,end):復制[begin,end)區間內另一個數組的元素到vector中
• void push_back(const T& x):向量尾部增加一個元素X
• iterator insert(iterator it,const T& x):向量中迭代器指向元素前增加一個元素x
• iterator erase(iterator it):刪除向量中迭代器指向元素
• void pop_back():刪除向量中最后一個元素
• void clear():清空向量中所有元素

2.set容器

• 所有元素都會根據元素的鍵值自動排序，set元素的鍵值就是實值，實值就是鍵值。set不允許兩個元素有相同的鍵值
  set成員函數列表如下:
• begin()--返回指向第一個元素的迭代器
• clear()--清除所有元素
• empty()--如果集合為空，返回true
• erase()--刪除集合中的元素
• find()--返回一個指向被查找到元素的迭代器
• insert()--在集合中插入元素
• size()--集合中元素的數目
  　
  3.map容器
  map可以同時擁有實值(value)和鍵值(key)，其余用法和set差不多

此次圖的學習，感覺好像比樹更簡單，實際卻考的更差。平時自己做題要想好久，等考前考后再去做的時候，思路好像更清晰了，不知是見多不怪還是熟能生巧。做題中發現除非要刪除、增加之類的問題，不然還是少用鄰接表吧，用的時候超容易出錯，鄰接矩陣的話，通俗易懂代碼量還更少，當然，能熟練使用容器更好了，非常方便。

2.PTA實驗作業

2.1.題目1：圖著色問題

給定無向圖G=(V,E)，問可否用K種顏色為V中的每一個頂點分配一種顏色，使得不會有兩個相鄰頂點具有同一種顏色？
但本題并不是要你解決這個著色問題，而是對給定的一種顏色分配，請你判斷這是否是圖著色問題的一個解。
輸入格式：
輸入在第一行給出3個整數V（0<V≤500）、E（≥0）和K（0<K≤V），分別是無向圖的頂點數、邊數、以及顏色數。頂點和顏色都從1到V編號。隨后E行，每行給出一條邊的兩個端點的編號。在圖的信息給出之后，
給出了一個正整數N（≤20），是待檢查的顏色分配方案的個數。隨后N行，每行順次給出V個頂點的顏色（第i個數字表示第i個頂點的顏色），數字間以空格分隔。題目保證給定的無向圖是合法的（即不存在自回路和重邊）。
輸出格式：
對每種顏色分配方案，如果是圖著色問題的一個解則輸出Yes，否則輸出No，每句占一行。
輸入樣例：
6 8 3
2 1
1 3
4 6
2 5
2 4
5 4
5 6
3 6
4
1 2 3 3 1 2
4 5 6 6 4 5
1 2 3 4 5 6
2 3 4 2 3 4
輸出樣例：
Yes
Yes
No
No

2.1.1設計思路

- 定義vector和set容器來做
- 根據輸入各店之間的關系來將元素a放在b的后面，b放在a的后面，類似于建鏈接表的的過程
- 依次輸入num組數據
    - flag初始化為1
    - 每次都需將容器 s 清空
    - 依次輸入各點對應的顏色，將顏色插入到容器 s 中（此處相同color只記一次）
    - 如果容器 s 大小不等于顏色總數k
        - flag=0該涂色方案不可行
    - 遍歷每個節點
        - 遍歷與該節點相鄰的節點
            - 如果兩相鄰節點顏色相同
                - 不符合涂色方案，跳出循環
        - 如果flag=0不符合，跳出循環
    - if（flag=1）輸出符合方案
    - 否則，輸出不符合

2.1.2代碼截圖

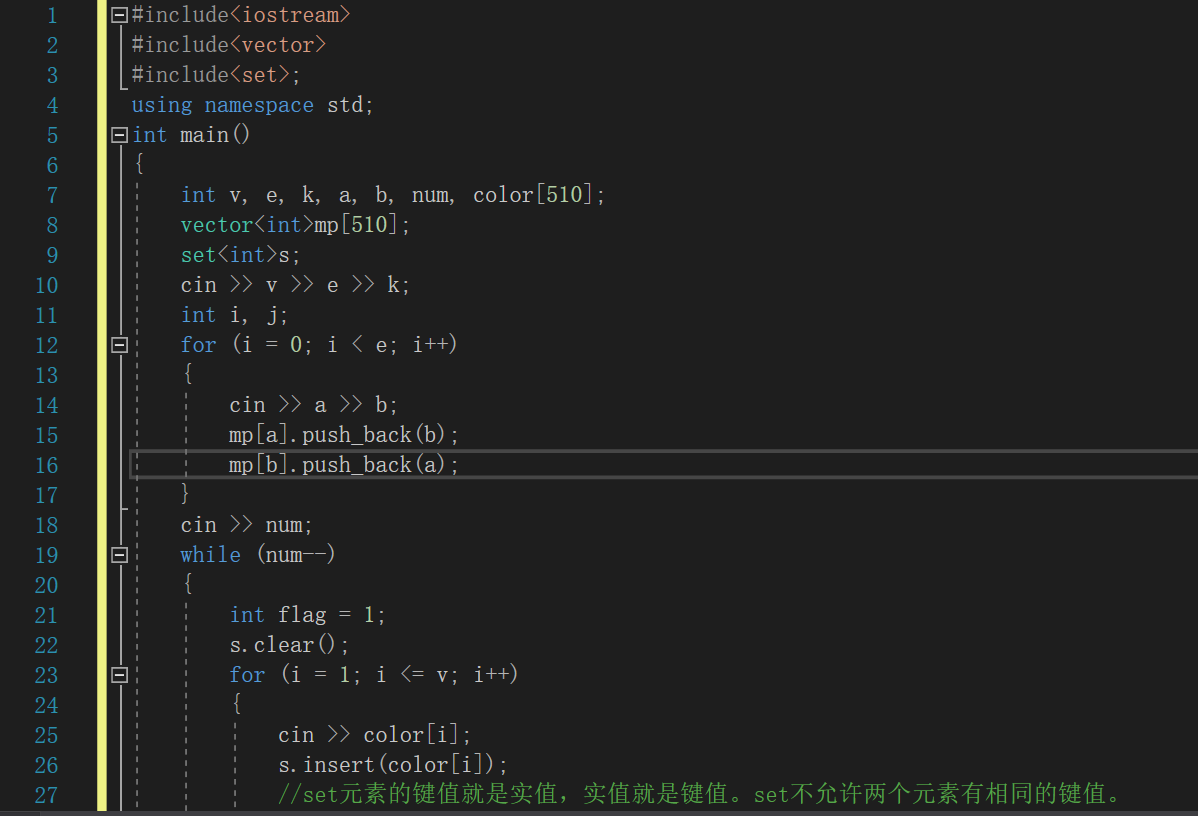
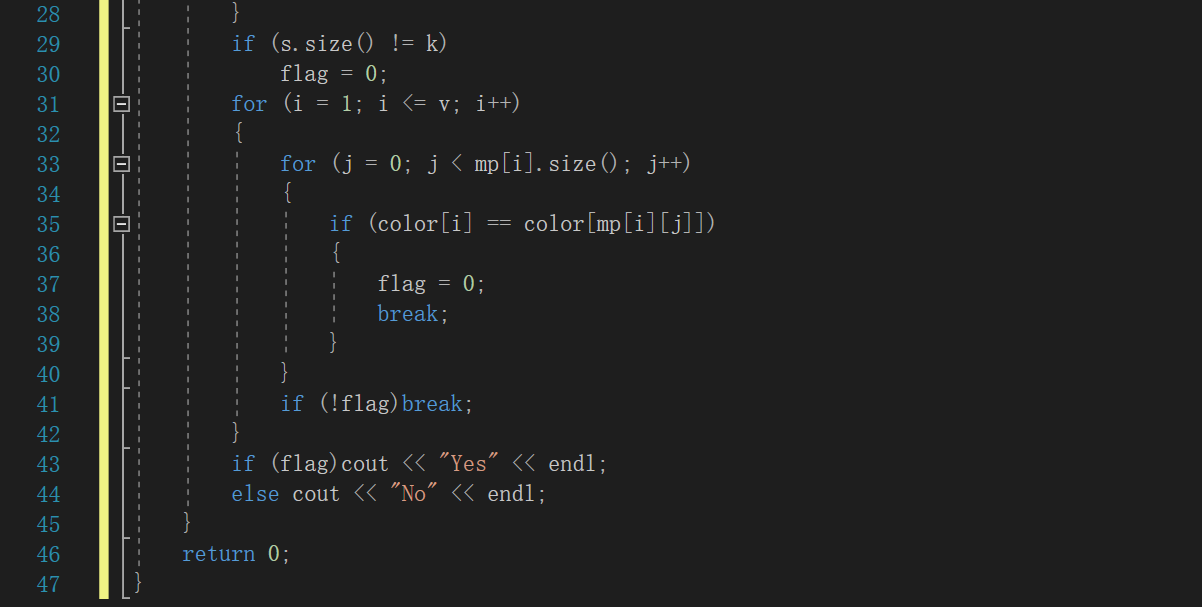
2.1.3本題PTA提交列表說明

• Q1:不知如何將顏色存入節點信息，發現存入data里面待會next又沒有data這個類型
• A1:改成鄰接矩陣，定義中間變量num[i]存儲顏色，并用哈希數組判斷顏色種類是否合理
• A2:發現改成容器做更方便，也不用進行建圖操作什么的，直接調用函數判斷有沒有相等，代碼量減少一半且方便易懂

2.2 題目2：六度空間

“六度空間”理論又稱作“六度分隔（Six Degrees of Separation）”理論。這個理論可以通俗地闡述為：“你和任何一個陌生人之間所間隔的人不會超過六個，也就是說，最多通過五個人你就能夠認識任何一個陌生人。
假如給你一個社交網絡圖，請你對每個節點計算符合“六度空間”理論的結點占結點總數的百分比。
輸入格式:
第1行給出兩個正整數，分別表示社交網絡圖的結點數N（1<N≤10000，表示人數）、邊數M（≤33×N，表示社交關系數）。隨后的M行對應M條邊，每行給出一對正整數，分別是該條邊直接連通的兩個結點的編號（節點從1到N編號）。
輸出格式:
對每個結點輸出與該結點距離不超過6的結點數占結點總數的百分比，精確到小數點后2位。每個結節點輸出一行，格式為“結點編號:（空格）百分比%”。
輸入樣例:
10 9
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10
輸出樣例:
1: 70.00%
2: 80.00%
3: 90.00%
4: 100.00%
5: 100.00%
6: 100.00%
7: 100.00%
8: 90.00%
9: 80.00%
10: 70.00%

2.2.1設計思路

利用廣度遍歷逐層遍歷圖，并記錄層數
該題和前面函數題廣度遍歷差不多，同時結合了樹的按層來劃分思想
- bfs函數：
初始化各點為未訪問狀態
將第一個節點z入隊同時標記他為已訪問狀態
當隊不空的時候
    z記錄隊首元素后即可將隊首出隊
    遍歷其他節點
        if（和該點為相鄰接點且未被訪問過）
            能通過六度空間認識的陌生人加一
            將該節點入隊并標記為已訪問
            tail記住最后一個入隊節點的位置
        if（隊首元素和存放的一層最后一個元素相等）
            層數加一
            last更新為tail的值
        if（層數=6）不符合六度空間要求，此時跳出循環
    return回count

- main函數
循環讀入邊之間關系
遍歷節點
    m接收bfs返回的count
    m/v*100即為輸出的答案

2.2.2代碼截圖

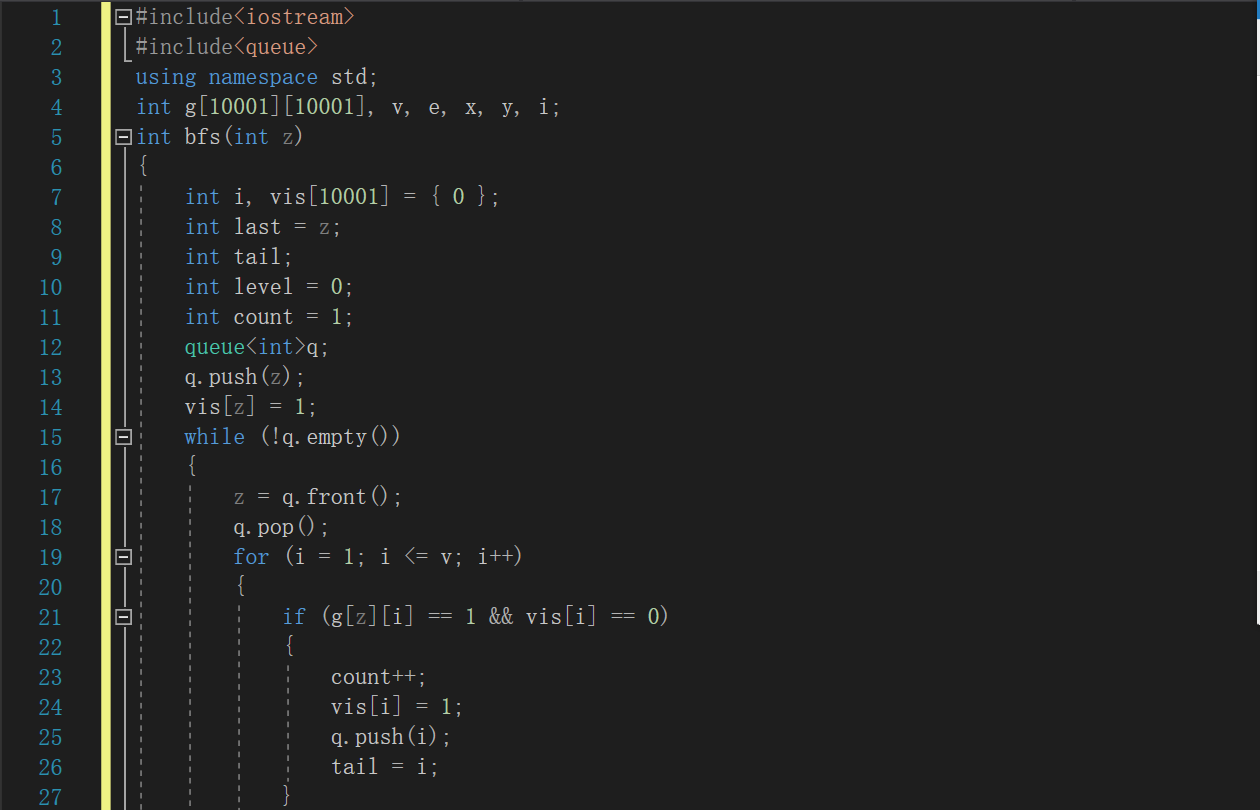
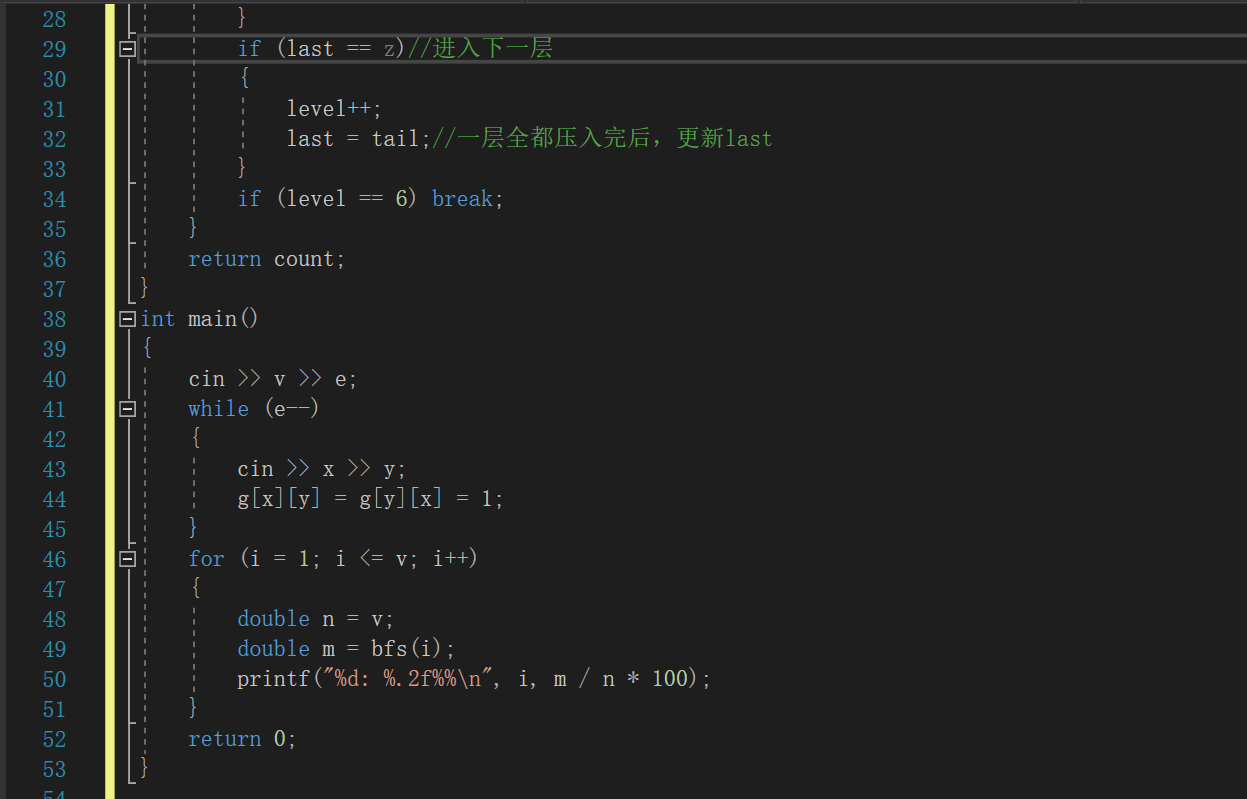
2.2.3ＰＴＡ提交列表及說明

• A1:我發現好幾題我用鄰接表做都錯誤百出，用鄰接矩陣一樣的思路交上去反而對了，所以綜上，還是能用鄰接矩陣就不用鄰接表
• A2:后面我去百度了一下，發現用鄰接表那個運行時錯誤是因為自己直接把函數題代碼復制過來，數組不夠大導致越界
• A3:下面總結幾種運行時錯誤的原因
  • 數組越界訪問（數組開大即可）
  • 除數為零
  • 堆棧溢出（大多是遞歸口出問題）
  • 使用失效的迭代器

2.3 題目3：公路村村通

現有村落間道路的統計數據表中，列出了有可能建設成標準公路的若干條道路的成本，求使每個村落都有公路連通所需要的最低成本。
輸入格式:
輸入數據包括城鎮數目正整數N（≤1000）和候選道路數目M（≤3N）；隨后的M行對應M條道路，每行給出3個正整數，分別是該條道路直接連通的兩個城鎮的編號以及該道路改建的預算成本。為簡單起見，城鎮從1到N編號。
輸出格式:
輸出村村通需要的最低成本。如果輸入數據不足以保證暢通，則輸出?1，表示需要建設更多公路。
輸入樣例:
6 15
1 2 5
1 3 3
1 4 7
1 5 4
1 6 2
2 3 4
2 4 6
2 5 2
2 6 6
3 4 6
3 5 1
3 6 1
4 5 10
4 6 8
5 6 3
輸出樣例:
12

2.３.1設計思路

main函數
初始化權重為無窮
讀入邊之間的權重關系

Prim函數
循環將節點1的相鄰邊之間的權重存入數組lowcost，作為最小權重
for循環找出n-1個節點的最小權重
    for循環遍歷各個節點
        if（權重不為0且不為無窮）
            min記住此時權重，k記住該節點 j
    if（min為無窮）
        非連通圖，返回-1
    num加上此時min，為修路最小花費
    for（遍歷節點調整邊關系）
        if（權重不為0且兩點間權重小于lowcost存的）
            調整lowcost為該權重，同時 j 的closest值改為k
    end for
end for
輸出最小花費num

2.３.2代碼截圖

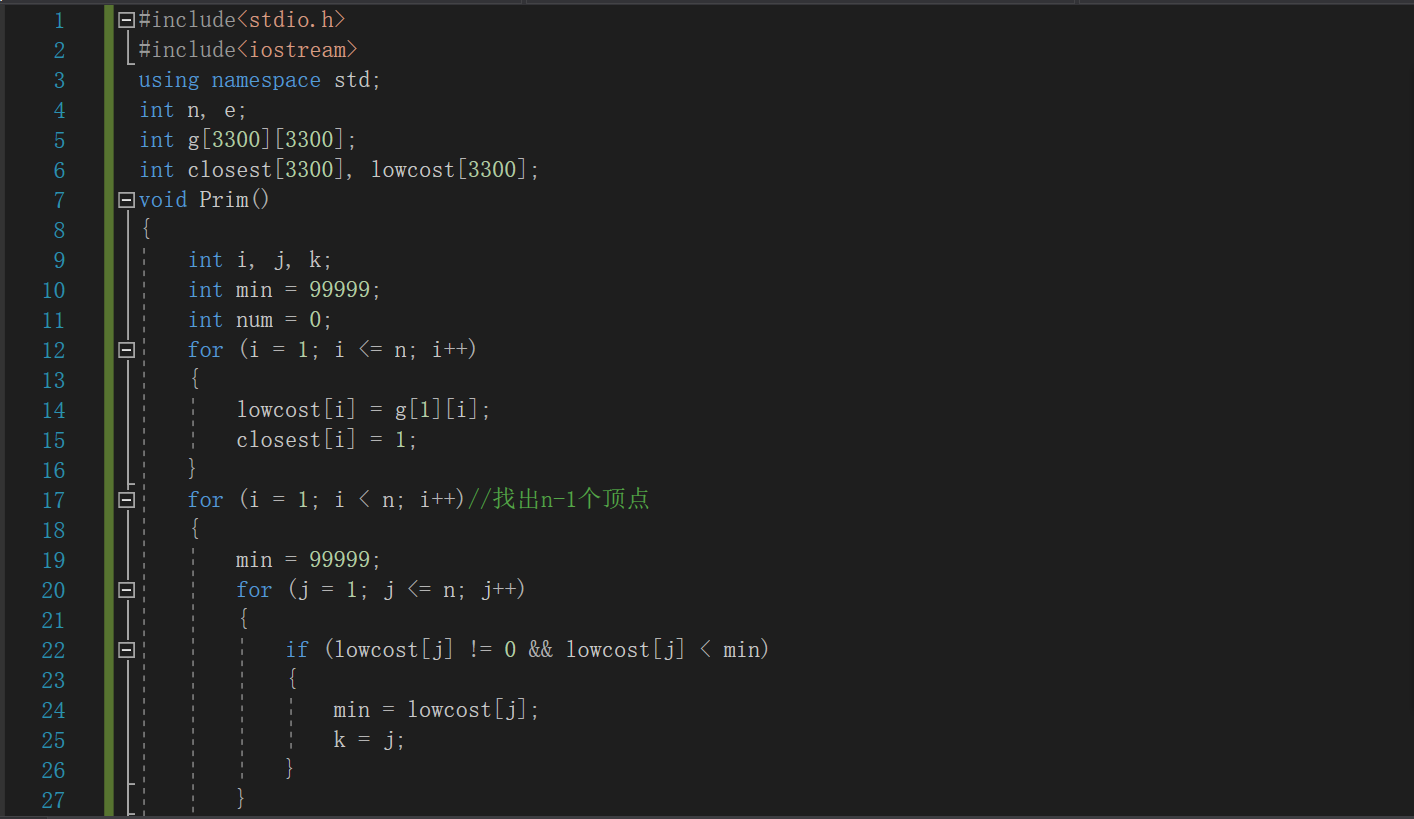
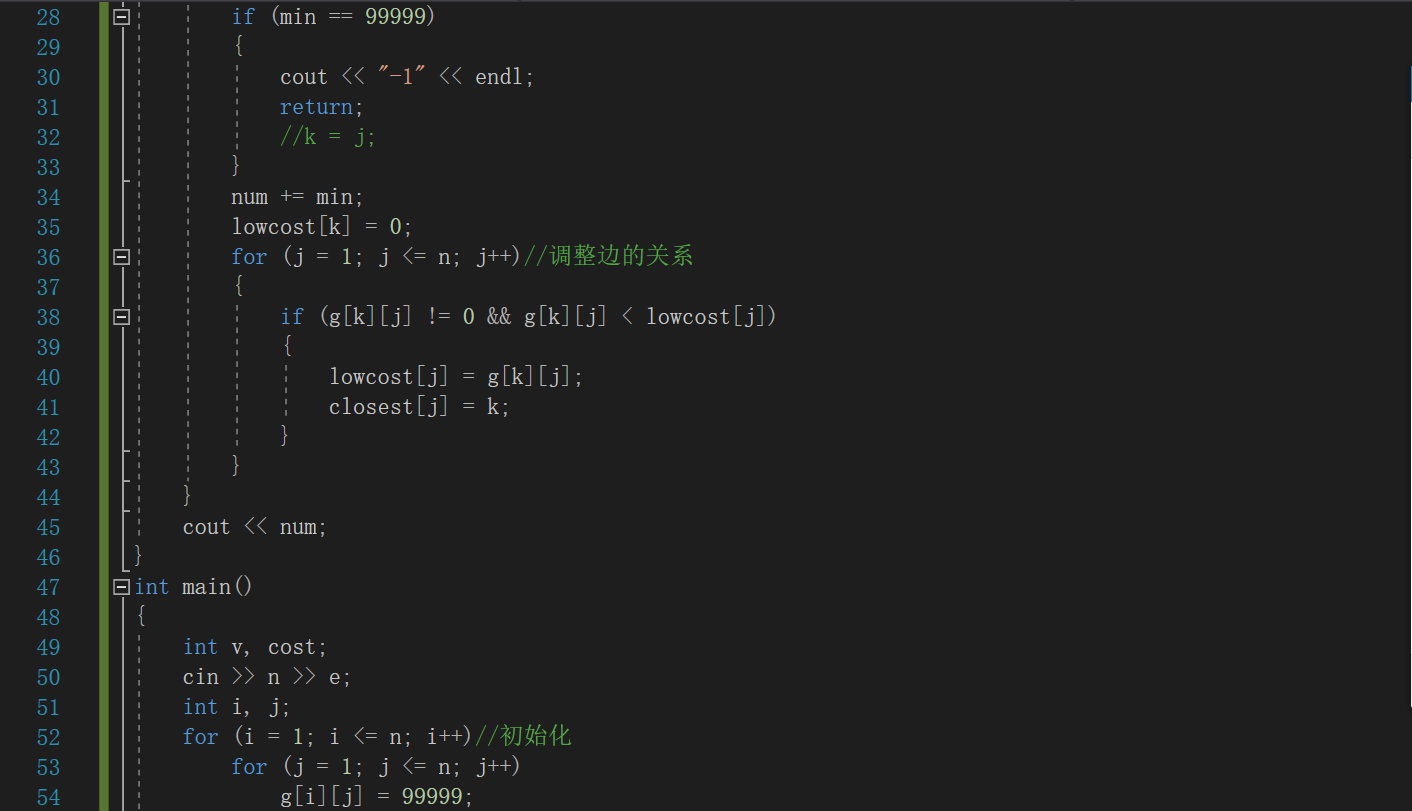
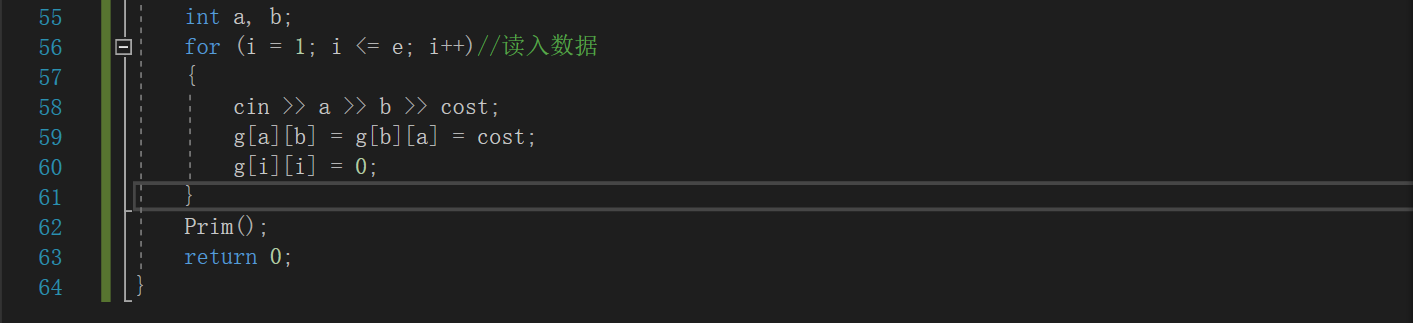
2.３.3ＰＴＡ提交列表及說明

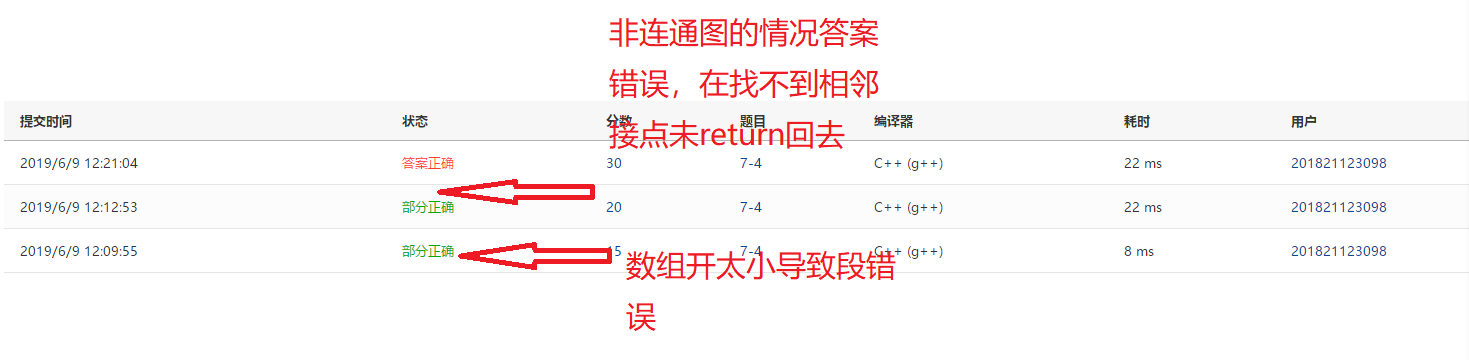
• 刪除k=j該句即可

3、上機考試錯題及處理辦法

3.1.拓撲排序

當時在深度廣度函數題那里耗了好久，思路看著沒錯一直過不去，vs又不好用，拿到dev又不能給我指出明確的錯誤，真的是很急。后面一直通過目測，發現是多次new導致有問題，然后拓撲排序就只剩半個小時，只寫了一半就交了，但源代碼也有錯誤

• 源代碼
  
  

3.2 錯的原因及處理方法

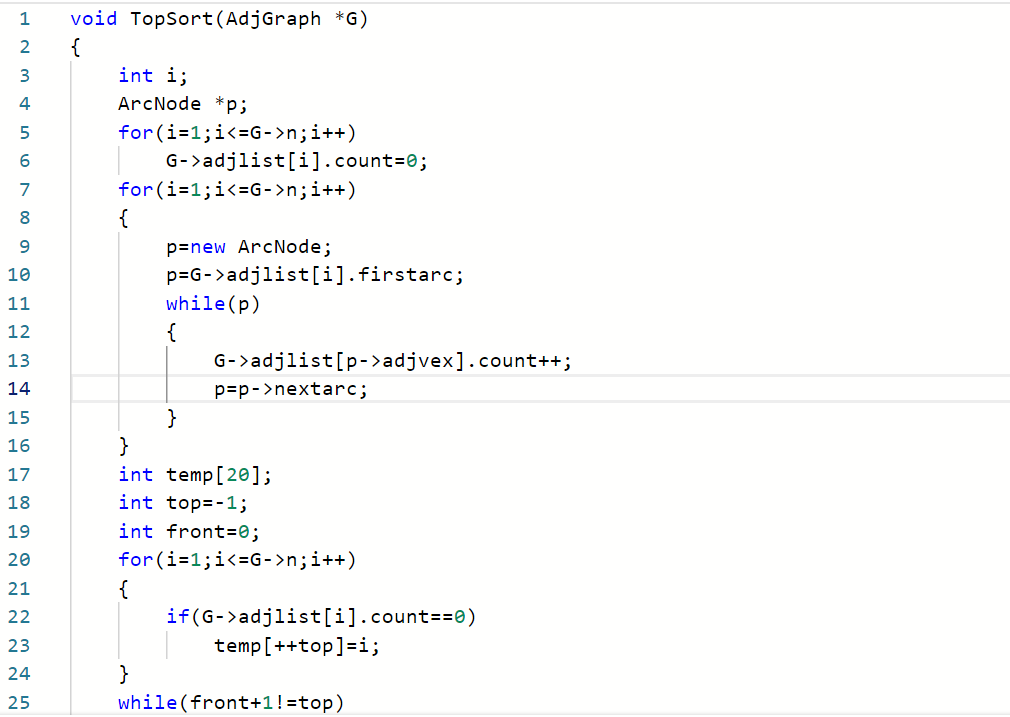
• 改正并且補齊后的代碼如下

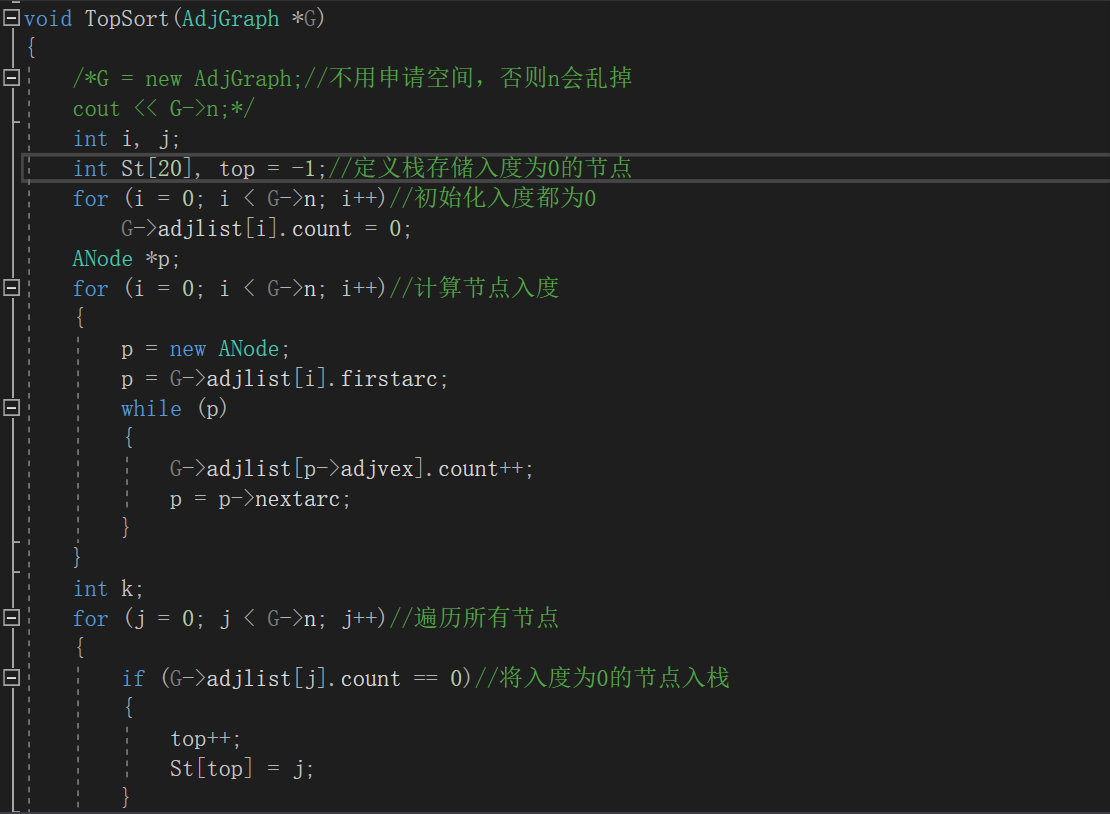
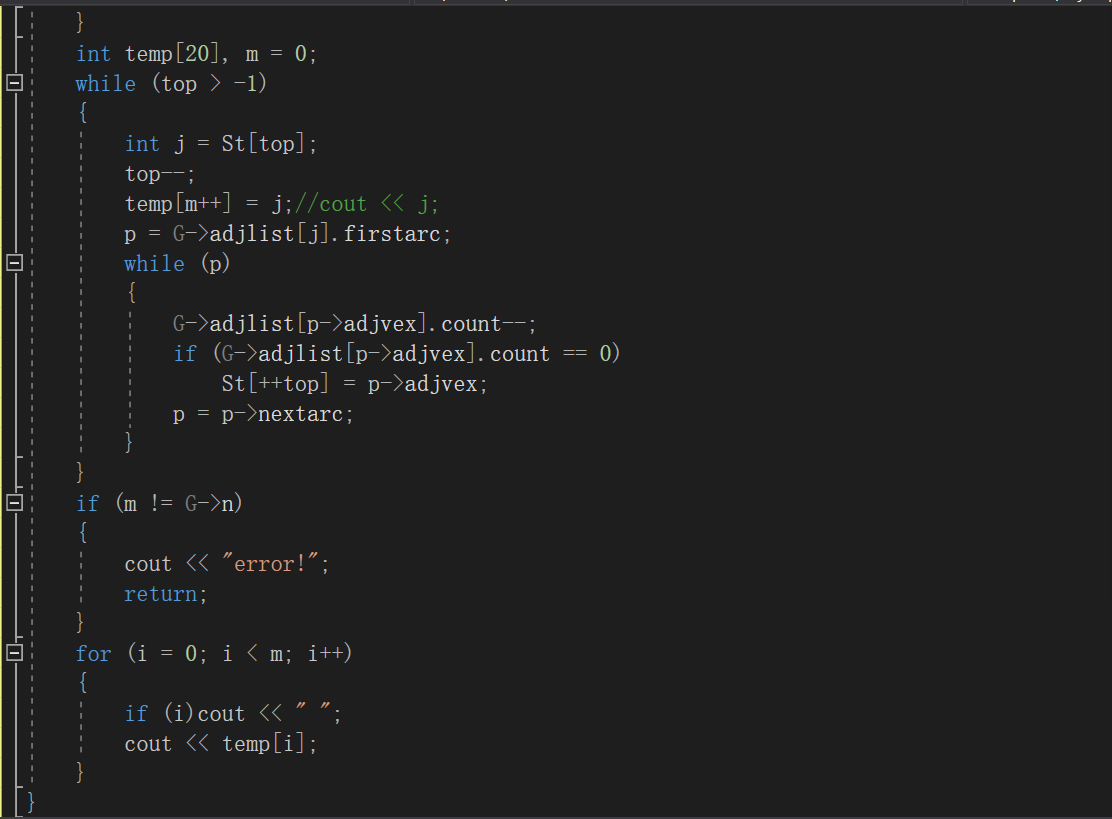
• 總結

圖結構主要是自己練的不夠多，他需要自己代碼思路不是很多，直接套用模板就可以做出來，就深度廣度遍歷和那幾種算法。在上機考時真沒想到自己一題函數題都能改那么久才對。思路腦海里是有的，主要是一些細節問題，常不注意，而且自己閱讀代碼能力比較弱，無法馬上知道錯誤，要經過好久的調試才會靈感一線，發現原來是這樣。今后學習還得多學習他人優秀代碼，哪怕是照著打一遍，都比看上個三四遍強。關于c++一些庫函數的知識我正在積累并逐漸學者應用到實際中，積少成多，總會有收獲的。