搜索算法1——聊聊dfs與回溯

目錄

1.dfs 的概念

$\ \ \ $1.1 dfs 的概念

2.dfs 的做法

$\ \ \ $2.1 為什么要用 dfs

$\ \ \ $2.2 dfs 如何實(shí)現(xiàn)

$\ \ \ $2.3 復(fù)雜度分析

3. 回溯法

$\ \ \ $3.1 回溯法的概念

$\ \ \ $3.2 回溯法的實(shí)現(xiàn)

1.dfs的概念

1.1.dfs的概念

dfs，即深度優(yōu)先搜索，顧名思義，深度優(yōu)先，就是不撞南墻不回頭，它每一次都會嘗試向更深的節(jié)點(diǎn)走。

在搜索里，dfs 一般指的是遞歸函數(shù)實(shí)現(xiàn)的暴力枚舉，一般時(shí)間復(fù)雜度是 \(O(!n)\)。

對于在圖論里的 dfs，這一章并不會介紹，有興趣的可以跳傘 此處待補(bǔ)。

2.dfs的做法

2.1.為什么要用dfs

我們看一道例題：

輸入正整數(shù) \(n\)，輸出由 \(1\) 到 \(n\) 這 \(n\) 個(gè)數(shù)取出 \(k\) 個(gè) \((1\le n\le 10,1\le k\le n)\) 的所有組合。

如果不用 dfs，那么這題該怎么辦呢？
循環(huán)唄。
\(k\) 重循環(huán)枚舉選哪個(gè)數(shù)，判斷重不重復(fù)，然后輸出即可。

但是這樣復(fù)雜度太超標(biāo)了，足足有 \(O(n^k)\)，最高有 \(O(10^{10})\)！

那么，就需要 dfs 來解決這個(gè)問題了。

2.2.dfs如何實(shí)現(xiàn)

我們可以先模擬一個(gè)樣例：

\(n=4,k=2\)

我們可以發(fā)現(xiàn)，用 2.1 中說的算法，過程如下（設(shè)第一重循環(huán)變量為 \(i\)，第二重循環(huán)變量為 \(j\)）：

i=1,j=1,重復(fù),跳過
i=1,j=2,輸出
i=1,j=3,輸出
i=1,j=4,輸出
i=2,j=1,重復(fù),跳過
i=2,j=2,重復(fù),跳過
i=2,j=3,輸出
i=2,j=4,輸出
i=3,j=1,重復(fù),跳過
i=3,j=2,重復(fù),跳過
i=3,j=3,重復(fù),跳過
i=3,j=4,輸出
i=4,j=1,重復(fù),跳過
i=4,j=2,重復(fù),跳過
i=4,j=3,重復(fù),跳過
i=4,j=4,重復(fù),跳過

其實(shí)，我們完全可以不遍歷這些重復(fù)的，以節(jié)約時(shí)間。

我們可以把枚舉"選哪個(gè)數(shù)"，變成"枚舉數(shù)"。

比如，我們可以先枚舉到 \(1\)，然后延伸出兩個(gè)分支——\(1\) 選和 \(1\) 不選。

然后這兩個(gè)分支分別往下枚舉又能分別延伸出兩個(gè)分支——\(2\) 選和 \(2\) 不選。

以此類推。

我們就可以畫出類似于這樣的一張圖：

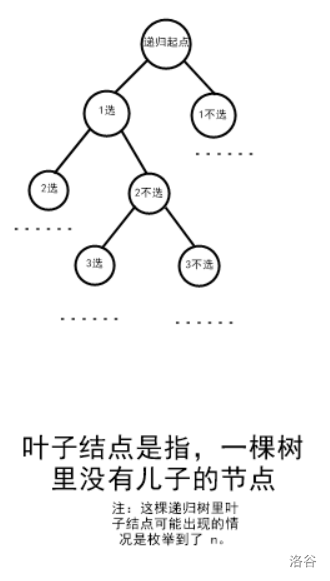
這就是遞歸樹（例子為 \(k=2\)）。

那么我們就知道了，我們可以從 \(1\) 開始枚舉，枚舉到 \(n\)，每一個(gè)數(shù)有兩種方案：選或不選，然后如果選了 \(k\) 個(gè)數(shù)就輸出。

但是，選或不選該怎么實(shí)現(xiàn)呢？

這就要用到 dfs 了。

dfs 是通過重復(fù)調(diào)用一個(gè)函數(shù)來實(shí)現(xiàn)的，例如：

void dfs(int dep,int cnt)//dep是當(dāng)前枚舉到的數(shù),cnt是選了幾個(gè)數(shù)
{
    if(dep==n+1)
    {
        if(cnt==k)
        {
            for(int i=0;i<cnt;i++)
            {
                printf("%d ",a[i]);//a[i]是記錄的選的數(shù)的集合
            }
        }
        return;//只枚舉到n,此處return是為了不繼續(xù)枚舉
    }
    a[cnt]=dep;//這里如果選的話,那么后面cnt+1,dep就存在集合里了,就完成了“選”這一操作.反之,如果不選,那么cnt不變,后面枚舉到的dep就覆蓋了a[cnt],達(dá)到不選的效果
    dfs(dep+1,cnt+1);//dep選
    dfs(dep+1,cnt+1);//dep不選
}

（注釋已經(jīng)很詳細(xì)了，應(yīng)該不用再講了吧）

2.3.復(fù)雜度分析

dfs 無剪枝復(fù)雜度一般都是 \(O(!n)\) 級別的。

記住就行。

3.回溯法

3.1.回溯法的概念

回溯法的本質(zhì)就是對于一棵遞歸樹，程序在遍歷時(shí)，如果發(fā)現(xiàn)遇到了邊界條件，就可以回去，搜另外的鏈。

3.2.回溯法的實(shí)現(xiàn)

看例題。

輸入正整數(shù) \(n\)，輸出由 \(1\) 到 \(n\) 這 \(n\) 個(gè)數(shù) \((n\le 7)\) 的所有排列，每行一個(gè)排列，數(shù)與數(shù)之間有一個(gè)空格，兩個(gè)排列中，第一個(gè)數(shù)小的優(yōu)先輸出，第一個(gè)數(shù)相同，比較第二個(gè)數(shù)，后面以此類推。

對于這一題，如果我們再用上面的方法，就會漏選。

而由于是 \(n\) 個(gè)數(shù)選 \(n\) 個(gè)，所以我們甚至不用 \(cnt\)，只記錄 \(dep\) 即可。

那么回溯怎么實(shí)現(xiàn)呢？

看代碼（解析都在注釋里）：

void dfs(int dep)
{
	if(dep==n+1)//就是到達(dá)了邊界條件,這里直接輸出就行
	{
		for(int i=1;i<=n;i++)
		{
			printf("%d ",a[i]);
		}
		cout<<endl;
		return;
	}
	for(int i=1;i<=n;i++)
	{
		if(!biao[i])//表示i沒被選
		{
			biao[i]=1;//選i
			a[dep]=i;
			dfs(dep+1);//往下遞歸
			biao[i]=0;//這就是回溯的關(guān)鍵一步,這一行代碼目的在于在接著進(jìn)行for循環(huán)時(shí),不能被這一次遍歷到的i干擾,否則就會出現(xiàn)n個(gè)數(shù)選不完的情況
		}
	}
}

（也不講了，這個(gè)已經(jīng)很詳細(xì)了）

好了，那么搜索算法1就結(jié)束了，感謝大家的支持，我是_little_Cabbage_，我們搜索算法2再見！