【比賽記錄】2025CSP+NOIP 沖刺模擬賽合集Ｉ
主打一個聽勸。（難蚌
2025CSP-S模擬賽64
| A | B | C | D | Sum | Rank |
|---|---|---|---|---|---|
| 50 | 0 | 0 | - | 50 | 7/7 |
掛 155pts，掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛掛。
意難平，遂寫場上做法。
A. 小 Z 愛計數
首先按照時間排序。對于兩個數對 \((a,b)\) 和 \((a',b')\)，令 \(a<a'\)，則合法當且僅當滿足一下條件之一：
- 有歸零操作，\(|b'|+1\le a'-a\)
- 無歸零操作，\(|b-b'|\le a'-a\land a'-a-|b-b'|\equiv0\pmod2\)
注意 \((a_1,b_1)\) 需要與 \((0,0)\) 判斷。怒掛 50pts。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
using namespace std;
namespace asbt{
const int maxn=1e6+5;
int T,n,m;
struct node{
int t,v;
node(int t=0,int v=0):t(t),v(v){}
il bool operator<(const node &x)const{
return t<x.t;
}
}a[maxn];
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>T;
while(T--){
cin>>m>>n;
for(int i=1;i<=n;i++){
cin>>a[i].t>>a[i].v;
}
a[++n]=node();
sort(a+1,a+n+1);
for(int i=1;i<n;i++){
int x=a[i].v,y=a[i+1].v,z=a[i+1].t-a[i].t;
if(abs(y)+1<=z||abs(x-y)<=z&&(z-abs(x-y))%2==0);
else{
cout<<"No\n";
goto togo;
}
}
cout<<"Yes\n";
togo:;
}
return 0;
}
}
int main(){return asbt::main();}
B. 小 Z 愛劃分
首先考慮一個 \(O(n^2)\) 的 DP：設 \(f_i\) 表示 \(1\) 到 \(i\) 的所有劃分的和，于是有 \(f_i=\sum_{j=0}^{i-1}f_j\times(pre_i\oplus pre_j)^2\)。能拿 20pts。
對于 \(a\le255\) 的部分分，注意到值域很小，因此把所有 \(pre_j\) 全都插入字典樹，在葉子節點上累加答案即可。時間復雜度 \(O(nV)\)，20pts。
場上只有 T2 需要 freopen，我直接沒看見，怒掛 40pts。
正解考慮對每兩位計算答案，因為 \((c_1+c_2+\dots+c_k)^2=\sum_{i=1}^{k}\sum_{j=1}^{k}c_ic_j\)，所以對于第 \(x\) 位和第 \(y\) 位，\(f_j\) 能對 \(f_i\) 產生貢獻當且僅當這兩位都不相同，貢獻為 \(f_j\times2^{x+y}\)。于是記 \(sum_{j,x,k,y}\) 表示 \(pre\) 的第 \(j\) 位為 \(x\)，第 \(k\) 位為 \(y\) 的 \(f\) 之和即可線性對數方完成。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
using namespace std;
namespace asbt{
const int maxn=2e5+5,mod=1e9+7;
il int pls(int x,int y){
return x+y<mod?x+y:x+y-mod;
}
il void add(int &x,int y){
x=pls(x,y);
}
il int mns(int x,int y){
return x<y?x-y+mod:x-y;
}
il void sub(int &x,int y){
x=mns(x,y);
}
int T,n,a[maxn],f[maxn],sum[37][2][37][2],_2[67];
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>T;
_2[0]=1;
for(int i=1;i<=60;i++){
_2[i]=pls(_2[i-1],_2[i-1]);
}
while(T--){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
a[i]^=a[i-1];
}
f[0]=1;
memset(sum,0,sizeof(sum));
for(int i=0;i<=30;i++){
for(int j=0;j<=30;j++){
sum[i][0][j][0]=1;
}
}
for(int i=1;i<=n;i++){
f[i]=0;
for(int j=0;j<=30;j++){
for(int k=0;k<=30;k++){
int x=a[i]>>j&1,y=a[i]>>k&1;
f[i]=(sum[j][x^1][k][y^1]*1ll*_2[j+k]+f[i])%mod;
}
}
for(int j=0;j<=30;j++){
for(int k=0;k<=30;k++){
int x=a[i]>>j&1,y=a[i]>>k&1;
add(sum[j][x][k][y],f[i]);
}
}
}
cout<<f[n]<<'\n';
}
return 0;
}
}
int main(){return asbt::main();}
C. 小 Z 愛優化
首先考慮值域較小的部分分，考慮可行性 DP，設 \(f_{i,j,k}\) 表示考慮了 \(1\) 到 \(i\)，最大值為 \(j\)，最小值為 \(k\) 是否可行。假設現在加入了 \(t\)，前面的最大值為 \(j\)，于是 \(f_{i,\max(j,t)}\) 的 01 序列可以或上 \(f_{i-1/i-2,j}\) 的第 \(1\) 到 \(t\) 位，然后如果 \(f_{i-1/i-2,j}\) 的第 \(t+1\) 到 \(V\) 位有 \(1\) 那么 \(f_{i,\max(j,t),t}\leftarrow1\)。能拿 20pts。
在這個做法的基礎上離散化一下能再拿 \(n\le30\) 的 20pts。bitset 優化一下能拿 \(n\le1000\) 的 25pts。
卡空間失敗，怒掛 65pts。
考慮正解。當前這一坨東西已然難以優化，不妨換個思路（
枚舉最小值 \(c\)，強制要求所有組都 \(\ge c\)。設 \(f_i\) 表示考慮 \(1\) 到 \(i\)，最大值最小為多少。于是有轉移：
\[f_i=\min(\max(f_{i-1},a_i),\max(f_{i-2},a_i+a_{i-1}))
\]
當然 \(a_i\ge c\) 才能進行第一種轉移，\(a_i+a_{i-1}\ge c\) 才能進行第二種轉移。這東西寫成矩陣是滿足結合律的，于是考慮 DDP，有：
\[\begin{bmatrix}
f_i&f_{i-1}
\end{bmatrix}
=\begin{bmatrix}
f_{i-1}&f_{i-2}
\end{bmatrix}
\times\begin{bmatrix}
a_i&0\\
a_i+a_{i-1}&+\infty
\end{bmatrix}
\]
用線段樹維護，\(c\) 變化時將對應位置的矩陣更改一下即可。
Code
#include<bits/stdc++.h>
#define int long long
#define il inline
#define lid id<<1
#define rid id<<1|1
using namespace std;
namespace asbt{
const int maxn=2e5+5,inf=1e18;
int T,n,a[maxn];
struct node{
int val,pos;
node(int val=0,int pos=0):val(val),pos(pos){}
il bool operator<(const node &x)const{
return val<x.val||val==x.val&&pos<x.pos;
}
}b[maxn<<1];
struct juz{
int a[2][2];
il int*operator[](int x){
return a[x];
}
il juz operator*(juz x)const{
juz res;
for(int i:{0,1}){
for(int j:{0,1}){
res[i][j]=min(max(a[i][0],x[0][j]),max(a[i][1],x[1][j]));
}
}
return res;
}
}tr[maxn<<2];
il void pushup(int id){
tr[id]=tr[lid]*tr[rid];
}
il void build(int id,int l,int r){
if(l==r){
tr[id][0][0]=a[l],tr[id][0][1]=0;
tr[id][1][0]=a[l]+a[l-1],tr[id][1][1]=inf;
return ;
}
int mid=(l+r)>>1;
build(lid,l,mid);
build(rid,mid+1,r);
pushup(id);
}
il void upd(int id,int l,int r,int p,int v){
if(l==r){
if(tr[id][0][0]==v){
tr[id][0][0]=inf;
}
if(tr[id][1][0]==v){
tr[id][1][0]=inf;
}
return ;
}
int mid=(l+r)>>1;
if(p<=mid){
upd(lid,l,mid,p,v);
}else{
upd(rid,mid+1,r,p,v);
}
pushup(id);
}
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>T;
while(T--){
cin>>n;
int tot=0;
for(int i=1;i<=n;i++){
cin>>a[i];
b[++tot]=node(a[i],i);
b[++tot]=node(a[i]+a[i-1],i);
}
sort(b+1,b+tot+1);
build(1,1,n);
int ans=min(tr[1][0][0],tr[1][1][0])-b[1].val;
// cout<<b[1].val<<' '<<min(tr[1][0][0],tr[1][1][0])<<'\n';
for(int i=1;i<tot;i++){
upd(1,1,n,b[i].pos,b[i].val);
// cout<<"P "<<b[i].pos<<' '<<b[i].val<<'\n';
if(b[i].val!=b[i+1].val){
ans=min(ans,min(tr[1][0][0],tr[1][1][0])-b[i+1].val);
// cout<<"Q "<<b[i+1].val<<' '<<min(tr[1][0][0],tr[1][1][0])<<'\n';
}
}
cout<<ans<<'\n';
}
return 0;
}
}
signed main(){return asbt::main();}
D. 小 Z 愛考試
容易發現有些點必然會加上 \(w_i\)，有些點必然不會加。具體地，可將點分為三類：
- \(a_i<a_{b_i}\)，必然加上 \(w_i\)，稱為一類點
- \(a_i\ge a_{b_i}+w_{b_i}\)，必然不會加上 \(w_i\)，稱為二類點
- \(a_{b_i}\le a_i<a_{b_i}+w_{b_i}\)，需要通過 \(b_i\) 確定加不加，稱為三類點
于是哥們連邊 \(i\to b_i\)，得到一個基環樹森林。詢問 \(u\) 點的答案時，就不斷在樹上跑，直到跑到一個一類點或二類點停下。情況分為三類：
- 遇到了一類點。設一路上跑過的點為 \(p_1,p_2,\dots,p_k\)，那么只有這些點以 \(p_k,p_{k-1},\dots,p_1\) 的順序發生時答案為 \(a_u+w_u\)。這種情況的概率為 \(\frac{{n\choose k}(n-k)!}{n!}=\frac{1}{k!}\)。
- 遇到了二類點。因為二類點不會加，所以這一路上的點都不會加。
- 跑到了環里，全是三類點，還是不會加。
于是哥們只需要求在基環樹上從 \(u\) 開始跑到的第一個一類或二類點即可。不妨將它們統稱為黑點，三類點為白點。由于需要動態修改，考慮用數據結構維護。將基環樹分為樹和環兩部分。首先是樹上的部分，考慮重鏈剖分，對每個重鏈維護一個存儲所有黑點的 set，哥們要求的就是在這條鏈上第一個深度比 \(u\) 小的黑點，若沒有則一直往上跳到根。
如果子樹上沒有，那么就在環上找。還是給環開一個 set，給環上的點標號，哥們要找的就是第一個編號大于 \(u\) 的黑點。可能要繞一圈繞回來，斷環為鏈，將整個環存兩遍即可。
對于修改，只會影響 \(u\) 和所有 \(b_i=u\) 的 \(i\) 的類型。\(i\) 只有 \(3\) 個，暴力修改即可。時間復雜度 \(O(n\log^2n)\)。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
#define pb push_back
#define pii pair<int,int>
#define mp make_pair
#define fir first
#define sec second
#define lwrb lower_bound
#define uprb upper_bound
using namespace std;
namespace asbt{
const int maxn=2e5+5,mod=1e9+7;
int T,n,m,a[maxn],b[maxn],c[maxn],d[maxn];
int cid[maxn],ccnt,crn[maxn],chid[maxn],chnt;
int dep[maxn],sz[maxn],hes[maxn],top[maxn];
int inv[maxn],len[maxn],fa[maxn];
bool bla[maxn];
vector<int> e[maxn];
queue<int> q;
struct node{
int k,u;
node(int k=0,int u=0):k(k),u(u){}
il bool operator<(const node &x)const{
return k<x.k;
}
};
set<node> cir[maxn],chn[maxn];
il void dfs1(int u){
sz[u]=1;
int mxs=0;
for(int v:e[u]){
if(d[v]){
continue;
}
dep[v]=dep[u]+1;
fa[v]=u;
dfs1(v);
sz[u]+=sz[v];
if(mxs<sz[v]){
mxs=sz[v],hes[u]=v;
}
}
}
il void dfs2(int u){
if(!chid[u]){
chid[u]=++chnt;
top[u]=u;
}
if(bla[u]){
chn[chid[u]].insert(node(dep[u],u));
}
if(hes[u]){
chid[hes[u]]=chid[u];
top[hes[u]]=top[u];
dfs2(hes[u]);
}
for(int v:e[u]){
if(d[v]||v==hes[u]){
continue;
}
dfs2(v);
}
}
il pii query(int u){
int uu=u;
while(dep[u]){
auto it=chn[chid[u]].uprb(node(dep[u],u));
if(it==chn[chid[u]].begin()){
if(dep[top[u]]){
u=fa[top[u]];
}else{
u=top[u];
}
}else{
it=prev(it);
return mp(dep[uu]-it->k+1,it->u);
}
}
auto it=cir[cid[u]].lwrb(node(crn[u],u));
if(it==cir[cid[u]].end()){
return mp(-1,-1);
}else{
return mp(it->k-crn[u]+dep[uu]+1,it->u);
}
}
il void solve(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i]>>b[i]>>c[i];
d[b[i]]++;
e[b[i]].pb(i);
}
for(int i=1;i<=n;i++){
if(d[i]==0){
q.push(i);
}
if(a[i]<a[b[i]]||a[i]>=a[b[i]]+c[b[i]]){
bla[i]=1;
}
}
while(q.size()){
int u=q.front();
q.pop();
if(--d[b[u]]==0){
q.push(b[u]);
}
}
for(int i=1;i<=n;i++){
if(d[i]&&!cid[i]){
ccnt++;
int u=i;
do{
cid[u]=ccnt,crn[u]=++len[ccnt];
if(bla[u]){
cir[ccnt].insert(node(crn[u],u));
}
dfs1(u),dfs2(u);
u=b[u];
}while(u!=i);
do{
if(bla[u]){
cir[ccnt].insert(node(len[ccnt]+crn[u],u));
}
u=b[u];
}while(u!=i);
}
}
// for(int i=1;i<=n;i++){
// cout<<i<<' '<<cid[i]<<' '<<crn[i]<<' '<<chid[i]<<' '<<dep[i]<<'\n';
// }
while(m--){
int opt,u,cc;
cin>>opt>>u;
if(opt==3){
pii x=query(u);
int v=x.sec,len=x.fir;
// cout<<v<<' '<<len<<'\n';
if(~v&&a[v]<a[b[v]]){
cout<<(inv[len]*1ll*(a[u]+c[u])+(1-inv[len]+mod)*1ll*a[u])%mod<<'\n';
}else{
cout<<a[u]<<'\n';
}
}else{
cin>>cc;
(opt==1?a:c)[u]=cc;
bool t=a[u]<a[b[u]]||a[u]>=a[b[u]]+c[b[u]];
// cout<<bla[u]<<' '<<t<<'\n';
if(bla[u]&&!t){
chn[chid[u]].erase(node(dep[u],u));
if(cid[u]){
cir[cid[u]].erase(node(crn[u],u));
cir[cid[u]].erase(node(len[cid[u]]+crn[u],u));
}
}else if(!bla[u]&&t){
// puts("666");
chn[chid[u]].insert(node(dep[u],u));
if(cid[u]){
cir[cid[u]].insert(node(crn[u],u));
cir[cid[u]].insert(node(len[cid[u]]+crn[u],u));
}
}
bla[u]=t;
for(int v:e[u]){
bool t=a[v]<a[b[v]]||a[v]>=a[b[v]]+c[b[v]];
if(bla[v]&&!t){
chn[chid[v]].erase(node(dep[v],v));
if(cid[v]){
cir[cid[v]].erase(node(crn[v],v));
cir[cid[v]].erase(node(len[cid[v]]+crn[v],v));
}
}else if(!bla[v]&&t){
chn[chid[v]].insert(node(dep[v],v));
if(cid[v]){
cir[cid[v]].insert(node(crn[v],v));
cir[cid[v]].insert(node(len[cid[v]]+crn[v],v));
}
}
bla[v]=t;
}
}
}
for(int i=1;i<=n;i++){
a[i]=b[i]=c[i]=d[i]=0;
cid[i]=crn[i]=chid[i]=0;
dep[i]=sz[i]=hes[i]=top[i]=0;
len[i]=fa[i]=bla[i]=0;
e[i].clear();
}
for(int i=1;i<=ccnt;i++){
cir[i].clear();
}
for(int i=1;i<=chnt;i++){
chn[i].clear();
}
ccnt=chnt=0;
}
int main(){
ios::sync_with_stdio(0),cin.tie(0);
inv[0]=inv[1]=1;
for(int i=2;i<=2e5;i++){
inv[i]=(mod-mod/i)*1ll*inv[mod%i]%mod;
}
for(int i=2;i<=2e5;i++){
inv[i]=inv[i-1]*1ll*inv[i]%mod;
}
cin>>T;
while(T--){
solve();
}
return 0;
}
}
int main(){return asbt::main();}
HZOJ CSP-S模擬33
| A | B | C | D | Sum | Rank |
|---|---|---|---|---|---|
| 100 | 100 | 35 | 45 | 280 | 5/27 |
A. Divisors
\(m\) 很小，直接將每個 \(a\) 的貢獻加給它的所有約數即可，用 map 存每個數目前的倍數個數。時間復雜度 \(O(m\sqrt{a}\log n)\)。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
using namespace std;
namespace asbt{
int n,m,b[205];
map<int,int> c;
int main(){
freopen("div.in","r",stdin);
freopen("div.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0);
cin>>m>>n;
b[0]=m;
for(int i=1,x;i<=n;i++){
cin>>x;
for(int j=1;j<=x/j;j++){
if(x%j==0){
if(j<=m){
b[c[j]]--,b[++c[j]]++;
}
if(j!=x/j&&x/j<=m){
b[c[x/j]]--,b[++c[x/j]]++;
}
}
}
}
for(int i=0;i<=n;i++){
cout<<b[i]<<'\n';
}
return 0;
}
}
int main(){return asbt::main();}
B. Market
首先將時間維掃描線掃掉。此時一個直觀的做法是每加入一個物品就用它更新背包 DP，時間復雜度 \(O(n^2c+m)\)。注意到 \(c\) 很大而 \(v\) 很小，交換定義域和值域即可，查詢時二分一下，時間復雜度 \(O(n^2v+m\log nv)\)。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
#define uprb upper_bound
using namespace std;
namespace asbt{
const int maxn=2e5+5;
int n,m,ans[maxn];
ll f[maxn];
struct node{
int c,v,t,typ;
node(int c=0,int v=0,int t=0,int typ=0):c(c),v(v),t(t),typ(typ){}
il bool operator<(const node &x)const{
return t<x.t||t==x.t&&typ<x.typ;
}
}a[maxn];
int main(){
freopen("market.in","r",stdin);
freopen("market.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0);
cin>>n>>m;
int tot=0;
for(int i=1,c,v,t;i<=n;i++){
cin>>c>>v>>t;
a[++tot]=node(c,v,t);
}
for(int i=1,t,v;i<=m;i++){
cin>>t>>v;
a[++tot]=node(i,v,t,1);
}
sort(a+1,a+tot+1);
memset(f,0x3f,sizeof(f));
f[0]=0;
for(int i=1,c,v;i<=tot;i++){
c=a[i].c,v=a[i].v;
if(a[i].typ){
ans[c]=uprb(f+1,f+60001,v)-f-1;
}else{
for(int j=6e4;j>=v;j--){
f[j]=min(f[j],f[j-v]+c);
}
for(int j=6e4;j;j--){
f[j]=min(f[j],f[j+1]);
}
}
}
for(int i=1;i<=m;i++){
cout<<ans[i]<<'\n';
}
return 0;
}
}
int main(){return asbt::main();}
/*
5 2
5 5 4
1 3 1
3 4 3
6 2 2
4 3 2
3 8
5 9
*/
C. 連通性
記 \(1\) 到 \(n-m\) 為藍點，\(n-m+1\) 到 \(n\) 為紅點。
首先考慮合法的連通塊的形態。不難發現只有以下兩種：
- 若干個紅點組成的一個團。
- 若干個藍點組成的一個連通塊，伸出去若干條邊連著若干個紅點，紅點之間又連了若干條邊。
首先考慮第一部分。設 \(g_i\) 表示 \(i\) 個點形成若干個團的方案數。枚舉最后一個團有 \(j\) 個點，為了避免算重，強制選擇編號最小的點，即 \(i-1\choose j-1\)，有：
\[g_i=\sum_{j=1}^{i}g_j{i-1\choose j-1}
\]
然后是第二部分。設 \(dp_{i,j}\) 表示由 \(i\) 個藍點、\(j\) 個紅點組成若干個連通塊的方案數，于是有：
\[dp_{i,j}=\sum_{k=1}^{i}\sum_{l=0}^{j}dp_{i-k,j-l}{i-1\choose k-1}{j\choose l}f_k2^{\frac{l(l-1)}{2}}(2^k-1)^l
\]
其中 \(f_i\) 表示 \(i\) 個點構成一個連通塊的方案數，考慮它的轉移，不妨令 \(1\) 到 \(i-1\) 構成若干個連通塊，再分別與 \(i\) 連邊。記 \(h_j\) 表示此時已經有 \(j\) 個點與 \(i\) 連通，有：
\[h_j=\sum_{k=1}^{j}h_{j-k}f_k{i-j+k-2\choose k-1}(2^k-1)
\]
而 \(f_i\) 就是 \(h_{i-1}\)。
于是哥們可以求出答案：
\[ans=\sum_{i=0}^{m}{m\choose i}g_idp_{n-m,m-i}
\]
時間復雜度 \(O(n^4+Tn)\)。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
using namespace std;
namespace asbt{
const int mod=1e9+7;
int T,n,m,dp[105][105],f[105],h[105],g[105];
int C[105][105],_2[10005],_2_[105][105];
il int pls(int x,int y){
return x+y<mod?x+y:x+y-mod;
}
il int mns(int x,int y){
return x<y?x-y+mod:x-y;
}
il void add(int &x,int y){
x=pls(x,y);
}
il void sub(int &x,int y){
x=mns(x,y);
}
int main(){
freopen("connect.in","r",stdin);
freopen("connect.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0);
C[0][0]=1;
for(int i=1;i<=100;i++){
C[i][0]=1;
for(int j=1;j<=i;j++){
C[i][j]=pls(C[i-1][j-1],C[i-1][j]);
}
}
_2[0]=1;
for(int i=1;i<=1e4;i++){
_2[i]=pls(_2[i-1],_2[i-1]);
}
for(int i=0;i<=100;i++){
_2_[i][0]=1;
for(int j=1;j<=100;j++){
_2_[i][j]=_2_[i][j-1]*1ll*(_2[i]-1+mod)%mod;
}
}
f[1]=1;
for(int i=2;i<=100;i++){
h[0]=1;
for(int j=1;j<i;j++){
h[j]=0;
for(int k=1;k<=j;k++){
h[j]=(h[j-k]*1ll*f[k]%mod*C[i-j+k-2][k-1]%mod*(_2[k]-1+mod)+h[j])%mod;
}
}
f[i]=h[i-1];
}
g[0]=1;
for(int i=1;i<=100;i++){
for(int j=1;j<=i;j++){
g[i]=(g[i-j]*1ll*C[i-1][j-1]+g[i])%mod;
}
}
dp[0][0]=1;
for(int i=1;i<=100;i++){
for(int j=0;j<=100;j++){
for(int k=1;k<=i;k++){
for(int l=0;l<=j;l++){
dp[i][j]=(dp[i-k][j-l]*1ll*C[i-1][k-1]%mod*C[j][l]%mod*f[k]%mod*_2[l*(l-1)>>1]%mod*_2_[k][l]+dp[i][j])%mod;
}
}
}
}
cin>>T;
while(T--){
cin>>n>>m;
int ans=0;
for(int i=0;i<=m;i++){
ans=(C[m][i]*1ll*g[i]%mod*dp[n-m][m-i]+ans)%mod;
}
cout<<ans<<'\n';
}
return 0;
}
}
int main(){return asbt::main();}
D. 樹
首先可以想到將路徑上的邊全都縮到一塊，最后有多少個連通塊就是 \(2\) 的幾次冪。這可以直接用并查集維護當前鏈最頂端的邊實現。關鍵在于判無解。對每條邊設向上和向下兩種狀態，對于路徑的 lca，經過它的這兩條邊方向必定相反，而對于路徑上的其他點，經過它的這兩條邊方向必定相同，種類并查集即可。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
#define pb push_back
using namespace std;
namespace asbt{
const int maxn=3e5+5,mod=1e9+7;
int n,m,fa[maxn],dep[maxn],anc[maxn][20];
vector<int> e[maxn];
struct{
int u,v;
}a[maxn];
struct{
int fa[maxn<<1];
il void build(int n){
for(int i=1;i<=n;i++){
fa[i]=i;
}
}
il int find(int x){
return x!=fa[x]?fa[x]=find(fa[x]):x;
}
il void merge(int u,int v){
fa[find(u)]=find(v);
}
il bool check(int u,int v){
return find(u)==find(v);
}
il bool check(int x){
return x==find(x);
}
}D1,D2;
il void dfs(int u){
for(int v:e[u]){
if(v==fa[u]){
continue;
}
fa[v]=u,dep[v]=dep[u]+1;
anc[v][0]=u;
for(int i=1;i<=18;i++){
anc[v][i]=anc[anc[v][i-1]][i-1];
}
dfs(v);
}
}
il int lca(int u,int v){
if(dep[u]<dep[v]){
swap(u,v);
}
int ddp=dep[u]-dep[v],t=0;
while(ddp){
if(ddp&1){
u=anc[u][t];
}
t++,ddp>>=1;
}
if(u==v){
return u;
}
for(int i=18;~i;i--){
if(anc[u][i]!=anc[v][i]){
u=anc[u][i],v=anc[v][i];
}
}
return anc[u][0];
}
il int kth(int u,int k){
int t=0;
while(k){
if(k&1){
u=anc[u][t];
}
k>>=1,t++;
}
return u;
}
int main(){
// freopen("my.out","w",stdout);
freopen("usmjer.in","r",stdin);
freopen("usmjer.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0);
cin>>n>>m;
for(int i=1,u,v;i<n;i++){
cin>>u>>v;
e[u].pb(v),e[v].pb(u);
}
dfs(1),D1.build(n),D2.build(n<<1);
for(int i=1;i<=m;i++){
int u,v;
cin>>u>>v;
a[i]={u,v};
int x=lca(u,v);
if(u!=x&&v!=x){
int uu=kth(u,dep[u]-dep[x]-1);
int vv=kth(v,dep[v]-dep[x]-1);
D2.merge(uu,vv+n);
D2.merge(uu+n,vv);
}
while(dep[D1.find(u)]>dep[x]+1){
u=D1.find(u);
// cout<<u<<'\n';
D1.merge(u,fa[u]);
D2.merge(u,fa[u]);
D2.merge(u+n,fa[u]+n);
}
while(dep[D1.find(v)]>dep[x]+1){
v=D1.find(v);
// cout<<v<<'\n';
D1.merge(v,fa[v]);
D2.merge(v,fa[v]);
D2.merge(v+n,fa[v]+n);
}
}
// puts("666");
for(int i=1,u,v,x;i<=m;i++){
// cout<<i<<'\n';
u=a[i].u,v=a[i].v,x=lca(u,v);
// cout<<u<<' '<<v<<' '<<x<<' ';
if(u!=x&&v!=x){
u=kth(u,dep[u]-dep[x]-1);
v=kth(v,dep[v]-dep[x]-1);
// cout<<u<<' '<<v<<'\n';
D1.merge(u,v);
}
}
// puts("666");
int ans=1;
for(int i=2;i<=n;i++){
if(D2.check(i,i+n)){
cout<<0;
return 0;
}
if(D1.check(i)){
(ans<<=1)%=mod;
}
}
cout<<ans;
return 0;
}
}
int main(){return asbt::main();}
2025CSP-S模擬賽65（HZOJ CSP-S模擬34）
| A | B | C | D | Sum | Rank |
|---|---|---|---|---|---|
| 100 | 17 | 30 | 10 | 157 | 11/16（13/25） |
A. 最長不下降子序列
首先，哥們翻轉的必然是一段形如 \(222\dots2111\dots1222\dots2111\dots1\dots\dots222\dots2111\dots1\) 的一段，而最終的 LIS 必然是這一段前面的所有 \(1\)、這一段前半部分的 \(2\)、這一段后半部分的 \(1\) 和這一段后面的所有 \(2\)。這可以用調整法證明。于是哥們獲得了一個 \(O(n^3)\) 做法：枚舉這一段的左端點 \(l\) 和右端點 \(r\)，再枚舉中間 \(1\) 和 \(2\) 的分界點 \(k\)。哥們不妨把連續的相同的數字縮到一塊，假設有 \(cnt\) 段，設 \(f1_i\) 表示第 \(i\) 段及之前有多少個 \(1\)，\(f2_i\) 表示第 \(i\) 段及之前有多少個 \(2\)，于是這一段的答案為：
\[f1_l+(f2_k-f2_{l-1})+(f1_r-f1_k)+(f2_{cnt}-f2_r)
\]
于是可以考慮那個經典方法，移動右端點，用線段樹維護所有左端點的答案。用單調棧維護 \(f2_k-f1_k\) 的最大值的變化即可。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
#define lid id<<1
#define rid id<<1|1
using namespace std;
namespace asbt{
const int maxn=1e6+5,inf=1e9;
int n,a[maxn],f1[maxn],f2[maxn];
il int calc(){
int m1=0,m2=0;
for(int i=1;i<=n;i++){
if(a[i]==1){
m1++;
}else{
m2=max(m1,m2)+1;
}
}
return max(m1,m2);
}
struct{
int typ,len;
}b[maxn];
int tr[maxn<<2],tag[maxn<<2],stk[maxn],top;
il void pushup(int id){
tr[id]=max(tr[lid],tr[rid]);
}
il void pushtag(int id,int v){
tag[id]+=v,tr[id]+=v;
}
il void pushdown(int id){
if(tag[id]){
pushtag(lid,tag[id]);
pushtag(rid,tag[id]);
tag[id]=0;
}
}
il void build(int id,int l,int r){
if(l==r){
tr[id]=b[l].typ==2?0:-inf;
return ;
}
int mid=(l+r)>>1;
build(lid,l,mid);
build(rid,mid+1,r);
pushup(id);
}
il void add(int id,int L,int R,int l,int r,int v){
if(L>=l&&R<=r){
pushtag(id,v);
return ;
}
pushdown(id);
int mid=(L+R)>>1;
if(l<=mid){
add(lid,L,mid,l,r,v);
}
if(r>mid){
add(rid,mid+1,R,l,r,v);
}
pushup(id);
}
int main(){
freopen("sequence.in","r",stdin);
freopen("sequence.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0);
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
int ans=calc(),cnt=0;
for(int i=1;i<=n;i++){
int j=i;
while(a[j+1]==a[i]){
j++;
}
b[++cnt]={a[i],j-i+1};
i=j;
}
for(int i=1;i<=cnt;i++){
f1[i]=f1[i-1],f2[i]=f2[i-1];
if(b[i].typ==1){
f1[i]+=b[i].len;
}else{
f2[i]+=b[i].len;
}
}
build(1,1,cnt);
for(int i=b[1].typ==1?3:2;i<=cnt;i+=2){
add(1,1,cnt,i-1,i-1,f2[i-1]-f2[i-2]+f2[cnt]);
while(top&&f2[i-1]-f1[i-1]>f2[stk[top]]-f1[stk[top]]){
add(1,1,cnt,stk[top-1]+1,stk[top],f2[i-1]-f1[i-1]-f2[stk[top]]+f1[stk[top]]);
top--;
}
stk[++top]=i-1;
ans=max(ans,f1[i]-f2[i]+tr[1]);
// cout<<i<<' '<<f1[i]-f2[i]+tr[1]<<'\n';
}
// for(int i=b[1].typ==1?2:1;i<=cnt;i+=2){
// for(int j=i+1;j<=cnt;j+=2){
// int res=0;
// for(int k=i;k<j;k+=2){
// res=max(res,f2[k]-f2[i-1]+f1[j]-f1[k]);
// }
// ans=max(ans,res+f1[i]+f2[cnt]-f2[j]);
// }
// }
cout<<ans;
return 0;
}
}
int main(){return asbt::main();}
B. 美食節
首先考慮無解情況，就是眾數的出現次數 \(>\lceil\frac{n}{2}\rceil\)。然后一位一位貪心。首先選擇與上一個數顏色不同的位置，考察選了它之后后面是否合法，若不合法則選擇當前的眾數即可。用 set 維護，時間復雜度線性對數。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
#define pii pair<int,int>
#define fir first
#define sec second
#define mp make_pair
using namespace std;
namespace asbt{
const int maxn=3e5+5;
int n,a[maxn],b[maxn];
set<int> st[maxn];
set<pii> s1,s2;
il void insert(int i){
if(b[a[i]]){
s2.erase(mp(b[a[i]],a[i]));
s1.erase(mp(*st[a[i]].begin(),a[i]));
}
st[a[i]].insert(i);
b[a[i]]++;
s1.insert(mp(*st[a[i]].begin(),a[i]));
s2.insert(mp(b[a[i]],a[i]));
}
il void erase(int i){
s1.erase(mp(*st[a[i]].begin(),a[i]));
s2.erase(mp(b[a[i]],a[i]));
st[a[i]].erase(i);
b[a[i]]--;
if(b[a[i]]){
s1.insert(mp(*st[a[i]].begin(),a[i]));
s2.insert(mp(b[a[i]],a[i]));
}
}
int main(){
freopen("food.in","r",stdin);
freopen("food.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0);
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
insert(i);
}
if(s2.rbegin()->fir>(n+1)>>1){
cout<<-1;
return 0;
}
for(int i=n-1,j=0;~i;i--){
int x=s1.begin()->fir;
if(a[x]==j){
x=next(s1.begin())->fir;
}
erase(x);
if(s2.size()&&s2.rbegin()->fir>(i+1)>>1){
insert(x);
// cout<<'|';
x=*st[s2.rbegin()->sec].begin();
erase(x);
}
j=a[x];
cout<<x<<' ';
}
return 0;
}
}
int main(){return asbt::main();}
C. 字符串
考慮枚舉對稱中心 \(i\)。只考慮 \(i\) 在 \(s\) 中的情況，在 \(t\) 中同理。
首先馬拉車出最大回文半徑。如果在 \(s\) 的范圍內，那么直接給答案貢獻即可。否則需要考慮和 \(t\) 拼接。考慮最大回文子串的左端點 \(l\)，哥們要做的就是將 \(s[1\dots l-1]\) 對所有 \(t\) 進行匹配，對 \(t\) 建 trie，樹上差分即可。但時間復雜度不能承受。于是將 trie 的所有前綴路徑插入哈希表，哈希二分出匹配的最大長度即可。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
#define ull unsigned ll
using namespace std;
namespace asbt{
const int maxn=1e5+5,maxm=2e6+5;
const ull bas=13331,mod=1999993;
int T,n,m,tr[maxm][26],sz[maxm],cnt[maxm],d[maxm],hd[maxm],hnm;
ll ans;
ull pw[maxm],ha[maxm];
string a[maxn],b[maxn];
struct{
int id,nxt;
ull val;
}hs[maxm];
il void insert(ull val,int id){
int p=val%mod;
hs[++hnm]={id,hd[p],val};
hd[p]=hnm;
}
il bool check(ull val){
int p=val%mod;
for(int i=hd[p];i;i=hs[i].nxt){
if(hs[i].val==val){
return 1;
}
}
return 0;
}
il void add(ull val){
int p=val%mod;
for(int i=hd[p];i;i=hs[i].nxt){
if(hs[i].val==val){
cnt[hs[i].id]++;
return ;
}
}
}
il void dfs1(int u,ull val){
for(int i=0;i<=25;i++){
if(tr[u][i]){
insert(val*bas+i+'a',tr[u][i]);
dfs1(tr[u][i],val*bas+i+'a');
}
}
}
il void dfs2(int u){
for(int i=0;i<=25;i++){
if(tr[u][i]){
dfs2(tr[u][i]);
cnt[u]+=cnt[tr[u][i]];
}
}
ans+=cnt[u]*1ll*sz[u];
}
il void manacher(string s,int n){
int l=0,r=-1;
for(int i=0;i<n;i++){
if(i>r){
int &j=d[i]=1;
while(i-j>=0&&i+j<n&&s[i-j]==s[i+j]){
j++;
}
if(r<i+j-1){
r=i+j-1,l=i-j+1;
}
}else{
int j=l+r-i,&k=d[i];
if(j-d[j]+1<=l){
k=r-i+1;
while(i-k>=0&&i+k<n&&s[i-k]==s[i+k]){
k++;
}
}else{
k=d[j];
}
if(r<i+k-1){
r=i+k-1,l=i-k+1;
}
}
}
}
il void work(int n,int m,string *a,string *b){
int tot=0;
sz[0]=cnt[0]=0;
for(int i=0;i<=25;i++){
tr[0][i]=0;
}
for(int i=1;i<=m;i++){
int p=0;
for(char j:b[i]){
if(!tr[p][j-'a']){
tr[p][j-'a']=++tot;
sz[tot]=cnt[tot]=0;
for(int j=0;j<=25;j++){
tr[tot][j]=0;
}
}
p=tr[p][j-'a'];
sz[p]++;
}
}
dfs1(0,0);
for(int i=1;i<=n;i++){
int kk=a[i].size();
ha[0]=1;
for(int j=kk-1;~j;j--){
ha[kk-j]=ha[kk-j-1]*bas+a[i][j];
}
manacher(a[i],kk);
// for(int j=0;j<kk;j++){
// cout<<d[j]<<' ';
// }
// cout<<'\n';
for(int j=0;j<kk;j++){
ans+=d[j]*1ll*m;
if(j+d[j]==kk){
int k=j-d[j];
int l=0,r=k+1;
while(l<r){
int mid=(l+r+1)>>1;
if(check(ha[kk-k+mid-1]-ha[kk-k-1]*pw[mid])){
l=mid;
}else{
r=mid-1;
}
}
add(ha[kk-k+l-1]-ha[kk-k-1]*pw[l]);
}
}
}
dfs2(0);
for(int i=1;i<=hnm;i++){
hd[hs[i].val%mod]=0;
}
hnm=0;
}
int main(){
freopen("str.in","r",stdin);
freopen("str.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0);
cin>>T;
pw[0]=1;
for(int i=1;i<=2e6;i++){
pw[i]=pw[i-1]*bas;
}
while(T--){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=m;i++){
cin>>b[i];
}
ans=0;
work(n,m,a,b);
// cout<<ans<<'\n';
for(int i=1;i<=n;i++){
reverse(a[i].begin(),a[i].end());
}
for(int i=1;i<=m;i++){
reverse(b[i].begin(),b[i].end());
}
work(m,n,b,a);
cout<<ans<<'\n';
}
return 0;
}
}
int main(){return asbt::main();}
/*
1
3 4
ryi
xvo
npr
zqcu
uvhz
fkgp
bbbb
90
*/
D. 概率
前 \(n\) 個數和后 \(n\) 個數是等價的，于是哥們求前后兩組和相等的概率即可。總方案數顯然，求合法方案數即可。
考慮將后 \(n\) 個數全都取相反數，哥們要求的就是前 \(n\) 個數 \(\in[0,m]\)，后 \(n\) 個數 \(\in[-m,0]\)，和為 \(0\) 的方案數。再給后 \(n\) 個數都加 \(m\)，就是求所有數都 \(\in[0,m]\)，和為 \(nm\) 的方案數。設這 \(2n\) 個數組成的集合為 \(A\)，于是有：
\[\begin{aligned}
& \sum_{\sum A=n m \text { 的方案 }}[A \text { 中 }>m \text { 的數的集合 }=\varnothing] \\
=&\sum_{\sum A=n m \text { 的方案 }} \sum_{T \subseteq(A \text { 中 }>m \text { 的數的集合 })}(-1)^{|T|} \\
=&\sum_{T \subseteq A}(-1)^{|T|}\left(T \text { 中的數都 }>m \text { 時 } \sum A=n m \text { 的方案數 }\right) \\
=&\sum_{i=0}^{2 n}(-1)^{i}\binom{2 n}{i}(i \text { 個 }>m \text { 的整數和 } 2 n-i \text { 個非負整數總和為 } n m \text { 的方案數 }) \\
=&\sum_{i=0}^{2 n}(-1)^{i}\binom{2 n}{i}(2 n \text { 個非負整數總和為 } n m-(m+1) i \text { 的方案數 }) \\
=&\sum_{i=0}^{2 n}(-1)^{i}\binom{2 n}{i}\binom{n m-(m+1) i+2 n-1}{2 n-1}
\end{aligned}
\]
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
using namespace std;
namespace asbt{
const int maxn=5e6+5;
int mod,T,n,m,fac[maxn],inv[maxn];
il int qpow(int x,int y=mod-2){
int res=1;
while(y){
if(y&1){
res=res*1ll*x%mod;
}
y>>=1,x=x*1ll*x%mod;
}
return res;
}
il void init(int n=5e6){
fac[0]=1;
for(int i=1;i<=n;i++){
fac[i]=fac[i-1]*1ll*i%mod;
}
inv[n]=qpow(fac[n]);
for(int i=n;i;i--){
inv[i-1]=inv[i]*1ll*i%mod;
}
}
il int C(int x,int y){
if(x<y||y<0){
return 0;
}
return fac[x]*1ll*inv[y]%mod*inv[x-y]%mod;
}
int main(){
freopen("pr.in","r",stdin);
freopen("pr.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0);
cin>>mod>>T;
init();
while(T--){
cin>>n>>m;
int ans=0;
for(int i=0;i<=n<<1;i++){
int t=C(n<<1,i)*1ll*C(n*m-(m+1)*i+2*n-1,2*n-1)%mod;
if(i&1){
ans=(ans-t+mod)%mod;
}else{
ans=(ans+t)%mod;
}
}
ans=(1-ans*1ll*qpow(qpow(m+1,n<<1))%mod+mod)*qpow(2)%mod;
cout<<ans<<'\n';
}
return 0;
}
}
int main(){return asbt::main();}
HZOJ CSP-S模擬35
| A | B | C | D | Sum | Rank |
|---|---|---|---|---|---|
| 10 | 50 | 15 | 5 | 80 | 9/27 |
A. 集合
將操作序列倒過來掃，用 bitset 可以直接維護出每個點在哪些點的集合內，時間復雜度 \(O(\frac{n^2}{w})\)。考慮容斥，\(|S\cup T|=|S|+|T|-|S\cap T|\)，發現對于同一條邊，上次操作得到的并集就是這次操作的交集，于是時間復雜度就線性了。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
using namespace std;
namespace asbt{
const int maxn=4e5+5;
int n,m,a[maxn],b[maxn],ans[maxn];
struct{
int u,v;
}e[maxn];
int main(){
freopen("set.in","r",stdin);
freopen("set.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0);
cin>>n>>m;
for(int i=1,u,v;i<n;i++){
cin>>u>>v;
e[i]={u,v};
}
for(int i=1;i<=n;i++){
ans[i]=1;
}
for(int i=1;i<=m;i++){
cin>>a[i];
}
for(int i=m;i;i--){
int u=e[a[i]].u,v=e[a[i]].v;
ans[u]=ans[v]=b[a[i]]=ans[u]+ans[v]-b[a[i]];
}
for(int i=1;i<=n;i++){
cout<<ans[i]<<' ';
}
return 0;
}
}
int main(){return asbt::main();}
B. 存錢
先把所有 \(a_i>m\) 都去掉，最后取個 \(\max\) 即可。
首先考慮 \(k=n-1\) 的情況。記第 \(a_i\) 的開頭為 \(p\)，由于要求兩個區間不被同一個長為 \(m\) 的區間包含，\(a_{i+1}\) 的結尾最小為 \(p+m\)，于是開頭就為 \(p+m-a_{i+1}+1\)，于是答案就為 \(m+1+\sum_{i=2}^{n}m-a_i+1\)。將最小的兩個放在首尾即可。
考慮 \(k=n-2\)，哥們顯然可以將所有 \(a\) 分為兩組，分別算出 \(k=n-1\) 的方案后再合并。具體地，先把最小的四個扔掉，設 \(b_i=m-a_i+1\)，兩組其中的一組為 \(S\)，于是答案就是 \(m+1+\max(\sum\limits_{i\in S}b_i,\sum\limits_{i\not\in S}b_i)\)。
記 \(\sum b_i=tot\)，哥們考慮盡量使 \(\sum\limits_{i\in S}b_i\) 接近 \(\frac{tot}{2}\)。首先從小到大在 \(b\) 中取使和 \(sum\le\frac{tot}{2}\) 直到不能取為止，記下一個位置為 \(p\)，哥們要做的就是當 \(sum<\frac{tot}{2}\) 時加進去一個 \(b_i\)，當 \(sum>\frac{tot}{2}\) 時減掉一個 \(b_i\)。顯然過程中 \(|sum-\frac{tot}{2}|\le m\)。設 \(f_{i,j}\) 表示當前考慮到了 \(i\)，湊出 \(\frac{tot}{2}+i\)，刪掉的最小的位置的最大值，于是可以轉移。轉移過程中每個位置只會被每個 \(j\) 考慮一次，于是時間復雜度 \(O(nm)\)。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
using namespace std;
namespace asbt{
const int maxn=1e4+5,M=5e3;
int T,n,m,kk,a[maxn],b[maxn],f[maxn],g[maxn];
int main(){
freopen("money.in","r",stdin);
freopen("money.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0);
cin>>T;
while(T--){
cin>>n>>m>>kk;
int mx=0;
for(int i=1;i<=n;i++){
cin>>a[i];
mx=max(mx,a[i]);
}
sort(a+1,a+n+1);
if(kk==n-1){
while(n&&a[n]>m){
n--;
}
int p=1;
for(int i=3;i<=n;i++){
p=p+m-a[i]+1;
}
mx=max(mx,p+m);
cout<<mx<<'\n';
continue;
}
while(n&&a[n]>m){
n--;
}
if(n<=2){
cout<<mx<<'\n';
continue;
}
if(n<=4){
cout<<max(mx,m+1)<<'\n';
continue;
}
int tot=0;
for(int i=n,j=1;i>=5;i--,j++){
b[j]=m+1-a[i];
tot+=b[j];
}
n-=4;
// for(int i=1;i<=n;i++){
// cout<<b[i]<<' ';
// }
// cout<<'\n';
int p=1,sum=0;
while(p<=n&&sum+b[p]<=tot>>1){
sum+=b[p++];
}
for(int i=0;i<=M<<1;i++){
f[i]=g[i]=0;
}
g[sum-tot/2+M]=p;
for(int i=p;i<=n;i++){
for(int j=0;j<=M<<1;j++){
f[j]=g[j];
}
for(int j=0;j<M;j++){
f[j+b[i]]=max(f[j+b[i]],g[j]);
}
for(int j=M<<1;j>M;j--){
for(int k=g[j];k<f[j];k++){
f[j-b[k]]=max(f[j-b[k]],k);
}
}
for(int j=0;j<=M<<1;j++){
g[j]=f[j];
}
}
int ans=0;
for(int i=M;~i;i--){
if(f[i]){
ans=tot/2+i-M;
break;
}
}
cout<<max(mx,tot-ans+m+1)<<'\n';
}
return 0;
}
}
int main(){return asbt::main();}
C. 串串
首先考慮如果 \(S\) 確定了怎么做。設 \(f_i\) 表示考慮到 \(T\) 的第 \(i\) 位，沒有匹配過 \(S\) 的方案數，\(g_i\) 表示考慮到 \(T\) 的第 \(i\) 位，只在最后面匹配了 \(S\) 的方案數。于是有轉移：
\[f_i=f_{i-1}\times k-g_i\\
g_i=f_{i-n}-\sum_{j\in\operatorname{border}}g_{i-n+j}
\]
注意到只和 \(\operatorname{border}\) 這個集合有關。考慮預處理出所有的 \(\operatorname{border}\) 集合與其對應的 \(S\) 的數量。這可以通過搜索 + 容斥處理。發現 \(\operatorname{border}\) 集合最多只有 \(4399\) 個，因此時間復雜度是對的。
Code
#include<bits/stdc++.h>
#define int long long
#define il inline
#define pii pair<int,int>
#define fir first
#define sec second
#define mp make_pair
#define pb push_back
using namespace std;
namespace asbt{
const int maxn=6e3+5,mod=1e9+7;
il int pls(int x,int y){
return x+y<mod?x+y:x+y-mod;
}
il int mns(int x,int y){
return x<y?x-y+mod:x-y;
}
il void add(int &x,int y){
x=pls(x,y);
}
il void sub(int &x,int y){
x=mns(x,y);
}
int n,m,kk,pw[maxn],fa[65],f[maxn],g[maxn];
vector<pii> bd;
il int find(int x){
return x!=fa[x]?fa[x]=find(fa[x]):x;
}
il void dfs(int x,int S){
if(!x){
for(int i=1;i<n;i++){
if(S>>(i-1)&1){
continue;
}
for(int j=1;j<=i;j++){
if(find(j)!=find(n-i+j)){
goto togo;
}
}
return ;
togo:;
}
int cnt=0;
for(int i=1;i<=n;i++){
if(i==find(i)){
cnt++;
}
}
bd.pb(mp(S,pw[cnt]));
return ;
}
for(int i=1;i<=x;i++){
if(find(i)!=find(n-x+i)){
int ff[65];
memcpy(ff,fa,(n+1)<<3);
dfs(x-1,S);
memcpy(fa,ff,(n+1)<<3);
break;
}
}
int ff[65];
memcpy(ff,fa,(n+1)<<3);
for(int i=1;i<=x;i++){
fa[find(i)]=find(n-x+i);
}
dfs(x-1,S|1ll<<(x-1));
memcpy(fa,ff,(n+1)<<3);
}
int main(){
freopen("string.in","r",stdin);
freopen("string.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0);
cin>>n>>m>>kk;
if(n>m){
cout<<0;
return 0;
}
pw[0]=1;
for(int i=1;i<=m;i++){
pw[i]=pw[i-1]*kk%mod;
}
for(int i=1;i<=n;i++){
fa[i]=i;
}
dfs(n-1,0);
sort(bd.begin(),bd.end(),greater<>());
for(int i=0;i<bd.size();i++){
for(int j=0;j<i;j++){
if((bd[i].fir&bd[j].fir)==bd[i].fir){
sub(bd[i].sec,bd[j].sec);
}
}
}
int ans=0;
for(pii BD:bd){
int S=BD.fir,cnt=BD.sec;
vector<int> vec;
for(int i=1;i<n;i++){
if(S>>(i-1)&1){
vec.pb(i);
}
}
f[0]=1,g[0]=0;
for(int i=1;i<=m;i++){
f[i]=g[i]=0;
if(i>=n){
g[i]=f[i-n];
for(int j:vec){
sub(g[i],g[i-n+j]);
}
}
f[i]=(f[i-1]*kk-g[i]+mod)%mod;
}
ans=((pw[m]-f[m]+mod)*cnt+ans)%mod;
}
cout<<ans;
return 0;
}
}
signed main(){return asbt::main();}
D. 游走
HZOJ CSP-S模擬36
| A | B | C | D | Sum | Rank |
|---|---|---|---|---|---|
| - | 50 | 5 | 70 | 125 | 11/29 |
其實 T1T3T4 都是之前考過的原。我是煞筆??
A. 島嶼
首先用暴力打個表：
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
#define pii pair<int,int>
#define fir first
#define sec second
#define mp make_pair
#define gcd __gcd
using namespace std;
namespace asbt{
int n,m,fa[39],sz[39],ans,tot,top,a[39],b[39],vis[39];
pii stk[39];
il int find(int x){
return x!=fa[x]?find(fa[x]):x;
}
il void merge(int u,int v){
u=find(u),v=find(v);
if(u==v){
return ;
}
if(sz[u]>sz[v]){
swap(u,v);
}
stk[++top]=mp(u,v);
fa[u]=v,sz[v]+=sz[u];
}
il void split(){
int u=stk[top].fir,v=stk[top].sec;
top--,fa[u]=u,sz[v]-=sz[u];
}
il void dfs(int x){
if(x>n){
tot++;
// for(int i=1;i<=n<<1;i++){
// for(int j=1;j<=n<<1;j++){
// cout<<vis[i][j];
// }
// cout<<'\n';
// }
// cout<<ans<<' ';
// puts("---------------");
// for(int i=1;i<=n;i++){
// cout<<a[vis[i]]<<' '<<b[i]<<'\n';
// }
// puts("---------------");
for(int i=1;i<=n<<1;i++){
if(i==find(i)){
ans++;
}
}
// cout<<ans<<'\n';
return ;
}
for(int i=1;i<=n;i++){
if(!vis[i]){
int tp=top;
merge(a[x],b[i]);
vis[i]=x;
dfs(x+1);
vis[i]=0;
if(top>tp){
split();
}
}
}
}
int main(){
printf(" |");
for(int i=0;i<=5;i++){
printf("%17d|",i);
}
puts("");
for(int i=0;i<=5;i++){
printf("----------------------------------------------------------");
puts("----------------------------------------------------------");
printf("%d|",i);
for(int j=0;j<=5;j++){
if(2*i+j>10){
break;
}
// cout<<i<<' '<<j<<":\n";
m=i,n=j;
n+=m<<1;
for(int k=1;k<=m;k++){
a[k]=k;
}
for(int k=m+1;k<=n;k++){
b[k-m]=k;
}
for(int k=n+1;k<=2*n-m;k++){
a[2*n-k+1]=k;
}
for(int k=2*n-m+1;k<=n<<1;k++){
b[k-n]=k;
}
// for(int k=1;k<=n;k++){
// cout<<a[k]<<' ';
// }
// cout<<'\n';
// for(int k=1;k<=n;k++){
// cout<<b[k]<<' ';
// }
// cout<<'\n';
for(int k=1;k<=n;k++){
fa[k]=fa[k+n]=k;
sz[k]=2;
}
tot=ans=0;
dfs(1);
// cout<<ans<<' '<<tot<<'\n';
printf("%8d/%8d|",ans/gcd(ans,tot),tot/gcd(ans,tot));
}
puts("");
}
printf("----------------------------------------------------------");
puts("----------------------------------------------------------");
return 0;
}
}
int main(){return asbt::main();}
打表
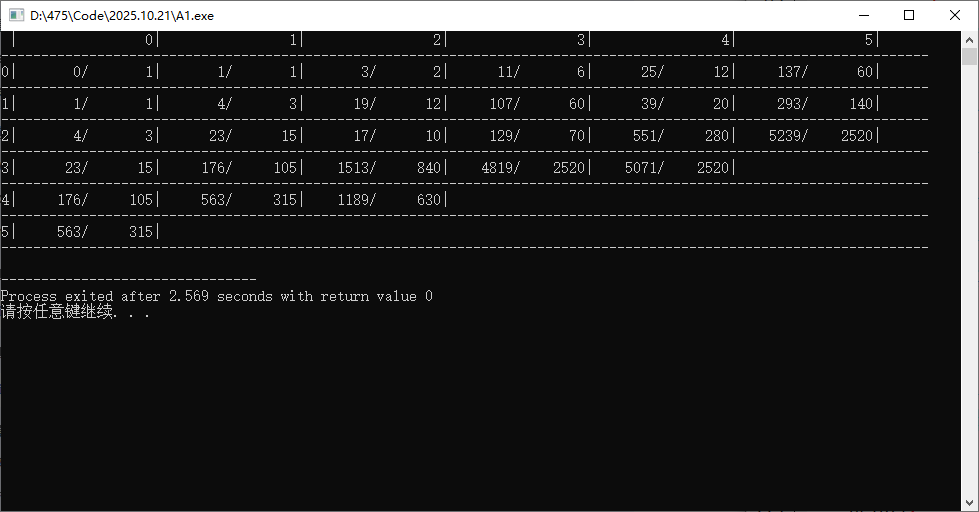
然后找規律。首先對于第一列，上下做差，哥們可以得到 \(f_{x,0}=f_{x-1,0}+\frac{1}{2x-1}\)。第二列的規律是類似的。但是第三列是難做的，考慮到哥們已經求出了第一列，只需要再求出 \(f_{x,y}-f_{x,y-1}\) 即可。于是哥們左右做差，發現 \(f_{x,y}=f_{x,y-1}+\frac{1}{2x+y}\)。于是得到了答案：
\[\sum_{i=1}^{x}\frac{1}{2i-1}+\sum_{i=1}^{y}\frac{1}{2x+i}
\]
時間復雜度線性。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
using namespace std;
namespace asbt{
int n,m;
int main(){
freopen("island.in","r",stdin);
freopen("island.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0);
cin>>n>>m;
double ans=0;
for(int i=1;i<=n;i++){
ans+=1.0/(2*i-1);
}
for(int i=1;i<=m;i++){
ans+=1.0/(2*n+i);
}
cout<<fixed<<setprecision(9)<<ans;
return 0;
}
}
int main(){return asbt::main();}
B. 小朋友
設 \(dp_{i,j}\) 表示在前 \(i\) 位中選了 \(j\) 位的最大的字符串，直接轉移即可，時間復雜度 \(O(n^3)\)。用 pair 好存一點。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
#define fir first
#define sec second
#define mp make_pair
using namespace std;
namespace asbt{
int n;
string a,b;
pair<string,string> dp[55][55];
int main(){
freopen("xiao.in","r",stdin);
freopen("xiao.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0);
cin>>a>>b;
n=a.size(),a=" "+a,b=" "+b;
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
dp[i][j]=max(dp[i-1][j],mp(dp[i-1][j-1].fir+a[i],dp[i-1][j-1].sec+b[i]));
}
}
string ans;
for(int i=1;i<=n;i++){
ans=max(ans,dp[n][i].fir+dp[n][i].sec);
}
cout<<ans;
return 0;
}
}
int main(){return asbt::main();}
C. 列表
Proposition 1：集合 \(S\) 合法當且僅當 \(\forall i\in[0,n]\)，列表中 \([n+1-i,n+1+i]\) 里 \(S\) 中的數的個數 \(\ge i+1\)。證明顯然。
Corollary：連續數字段 \(A\) 合法當且僅當 \(\forall i\in[0,n]\)，列表中 \([n+1-i,n+1+i]\) 外 \(A\) 中的數的個數 \(\le n-i\)。證明也顯然。
Proposition 2：若 \(A\) 合法，則 \(B\subseteq A\) 合法。證明依然顯然。
于是根據 Proposition 2，哥們雙指針枚舉連續數字段 \(A=[l,r]\)，然后用線段樹維護 \(\max_{i=0}^{n}i+p(i)\)（其中 \(p(i)\) 表示列表中 \([n+1-i,n+1+i]\) 以外 \(A\) 中的數的個數）即可。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
#define lid id<<1
#define rid id<<1|1
using namespace std;
namespace asbt{
const int maxn=4e5+5;
int n,a[maxn],b[maxn];
int tr[maxn<<2],tag[maxn<<2];
il void pushup(int id){
tr[id]=max(tr[lid],tr[rid]);
}
il void pushtag(int id,int v){
tag[id]+=v,tr[id]+=v;
}
il void pushdown(int id){
if(tag[id]){
pushtag(lid,tag[id]);
pushtag(rid,tag[id]);
tag[id]=0;
}
}
il void build(int id,int l,int r){
if(l==r){
tr[id]=l;
return ;
}
int mid=(l+r)>>1;
build(lid,l,mid);
build(rid,mid+1,r);
pushup(id);
}
il void add(int id,int L,int R,int l,int r,int v){
if(l>r){
return ;
}
if(L>=l&&R<=r){
pushtag(id,v);
return ;
}
pushdown(id);
int mid=(L+R)>>1;
if(l<=mid){
add(lid,L,mid,l,r,v);
}
if(r>mid){
add(rid,mid+1,R,l,r,v);
}
pushup(id);
}
int main(){
freopen("list.in","r",stdin);
freopen("list.out","w",stdout);
ios::sync_with_stdio(0),cin.tie(0);
cin>>n;
for(int i=1;i<=n*2+1;i++){
cin>>a[i];
b[a[i]]=i;
}
int ans=0;
build(1,0,n);
for(int l=1,r=0;l<=2*n+1;l++){
while(r<n*2+1){
r++;
int p=abs(b[r]-n-1);
add(1,0,n,0,p-1,1);
if(tr[1]>n){
add(1,0,n,0,p-1,-1);
r--;
break;
}
}
// cout<<l<<' '<<r<<'\n';
ans=max(ans,r-l+1);
int p=abs(b[l]-n-1);
add(1,0,n,0,p-1,-1);
}
cout<<ans;
return 0;
}
}
int main(){return asbt::main();}
浙公網安備 33010602011771號