【做題記錄】CF2600左右有趣的思維題1
A. Latin Square
考慮維護三元組 \((i,j,a_{i,j})\)。例如:R 操作就是變成了 \((i,j+1,a_{i,j})\);I 操作就是變成了 \((i,a_{i,j},j)\)。時間復雜度 \(O(m+n^2)\)。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
using namespace std;
namespace asbt{
const int maxn=1e3+5;
int T,n,m,a[maxn][maxn],b[maxn][maxn];
string s;
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>T;
while(T--){
cin>>n>>m;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
cin>>a[i][j];
a[i][j]--;
}
}
int pa=1,pb=2,pc=3;
int da=0,db=0,dc=0;
cin>>s;
for(char opt:s){
switch(opt){
case 'R':{
db++;
break;
}
case 'L':{
db--;
break;
}
case 'D':{
da++;
break;
}
case 'U':{
da--;
break;
}
case 'I':{
swap(pb,pc),swap(db,dc);
break;
}
default:{
swap(pa,pc),swap(da,dc);
break;
}
}
}
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
int aa=pa==1?i:pa==2?j:a[i][j];
int bb=pb==1?i:pb==2?j:a[i][j];
int cc=pc==1?i:pc==2?j:a[i][j];
aa=((aa+da)%n+n)%n;
bb=((bb+db)%n+n)%n;
cc=((cc+dc)%n+n)%n;
b[aa+1][bb+1]=cc+1;
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
cout<<b[i][j]<<' ';
}
cout<<'\n';
}
}
return 0;
}
}
int main(){return asbt::main();}
B. Even Split
顯然最小極差是可以二分出來的。check 不容易直接想,先考慮弱化版,假設已經知道了最短、最長的區間長度 \([x,y]\) 如何 check,線性掃一遍維護右端點區間即可。考慮如果這個 \(x\) 太大,即 \(\exist i,l>a_{i+1}\),則合法的 \(x'\) 必然滿足 \(x'<x\);如果 \(y\) 太小,即 \(\exist i,r<a_i\),則必然滿足 \(y'>y\),即 \(x'>x\),于是再二分 \(x'\) 即可。
考慮構造答案,先正向掃一遍使每一段滿足最小值的限制,再反過來掃一遍滿足最大值的限制即可,構造出的解必然合法。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
using namespace std;
namespace asbt{
const int maxn=1e5+5;
int n,m,a[maxn],mn,mx,b[maxn];
il int chk(int x,int y){
mn=x,mx=y;
int l=0,r=0;
for(int i=1;i<=n;i++){
if(l+x>a[i+1]){
return 1;
}
if(r+y<a[i]){
return -1;
}
l=max(a[i],l+x);
r=min(a[i+1],r+y);
}
if(l>m){
return 1;
}
if(r<m){
return -1;
}
return 0;
}
il bool check(int x){
int l=0,r=m;
while(l<r){
int mid=(l+r)>>1;
switch(chk(mid,mid+x)){
case 1:{
r=mid;
break;
}
case -1:{
l=mid+1;
break;
}
default:{
return 1;
break;
}
}
}
return 0;
}
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>m>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
a[n+1]=m;
int l=0,r=m;
while(l<r){
int mid=(l+r)>>1;
if(check(mid)){
r=mid;
}else{
l=mid+1;
}
}
check(l);
for(int i=1;i<=n;i++){
b[i]=max(b[i-1]+mn,a[i]);
}
b[n]=m;
for(int i=n;i;i--){
b[i-1]=max(b[i-1],b[i]-mx);
}
for(int i=1;i<=n;i++){
cout<<b[i-1]<<' '<<b[i]<<'\n';
}
return 0;
}
}
int main(){return asbt::main();}
C. Two Tanks
考慮一個非常 NB 的轉化,如圖,兩個水桶的范圍即為 \([-a,b]\),中間的藍色線段為水所在的范圍。要求是水條不能超過左右邊界,同時必須時刻覆蓋 \(0\) 這個點。
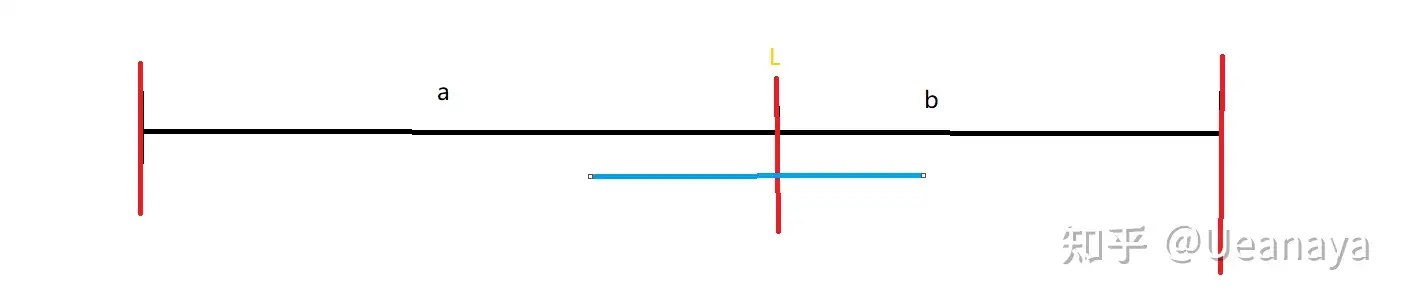
設所有的操作的前綴和為 \(s\),維護它的最大、最小值,考慮即使不考慮上面那些要求依然能滿足限制的水條初始左端點范圍 \(p\in[l,r]\)。記 \(x=c+d\)。于是有:
對于 \(p\in[l,r]\),答案即為 \(p+s_n\)。對于 \(p<l\),會抵到左邊界,與 \(l\) 答案相同;另一邊和 \(r\) 答案相同。模擬兩遍即可。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
using namespace std;
namespace asbt{
const int maxn=1e4+5,maxm=1e3+5;
int n,a,b,c[maxn],s[maxn],ans[maxm][maxm];
il int calc(int x,int y){
for(int i=1;i<=n;i++){
if(c[i]>0){
int t=min({x,c[i],b-y});
x-=t,y+=t;
}else{
int t=min({a-x,-c[i],y});
x+=t,y-=t;
}
}
return x;
}
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>n>>a>>b;
int mx=0,mn=0;
for(int i=1;i<=n;i++){
cin>>c[i];
s[i]=s[i-1]+c[i];
mx=max(mx,s[i]);
mn=min(mn,s[i]);
}
for(int x=0;x<=a+b;x++){
int l=max(-a-mn,-x-mn);
int r=min(-mx,b-mx-x);
int L=calc(-l,x+l);
int R=calc(-r,x+r);
for(int p=-a;p<=0;p++){
if(x+p<0||x+p>b){
continue;
}
if(p<l){
ans[-p][x+p]=L;
}else if(p>=l&&p<=r){
ans[-p][x+p]=-s[n]-p;
}else{
ans[-p][x+p]=R;
}
}
}
for(int i=0;i<=a;i++){
for(int j=0;j<=b;j++){
cout<<ans[i][j]<<' ';
}
cout<<'\n';
}
return 0;
}
}
int main(){return asbt::main();}
D. Magician and Pigs (Hard Version)
考慮每個 \(3\) 操作,設執行其前面的所有操作會減去 \(w\),那么對于當前生命值為 \(val\) 的小豬,其本質就是將它分裂成一個 \(val\) 和一個 \(val-w\)。\(w\) 是好求的,\(2\) 操作就加上,\(3\) 操作就翻倍。
對于插入的一個數 \(a\),其后面的 \(2\) 操作的影響是好處理的,\(3\) 操作則會分裂。注意到對于兩個三操作,其 \(w\) 值至少是翻倍的關系,因此 \(O(\log V)\) 次之后的三操作就沒用了。于是我們的問題變為對于一個集合 \(S\),滿足 \(S_i\ge2S_{i+1}\),問有多少個子集之和小于等于 \(a\),其中 \(a\) 要提前減去 \(2\) 操作的影響。顯然 \(|S|\le\log V\),那么直接枚舉每一位選不選,選則遞歸,不選則累加后面的所有貢獻即可。
但是一開始可能會有一段 \(w=0\)。這些操作的作用是使答案乘二,記錄一下就好了。時間復雜度 \(O(n\log V)\)。
Code
#include<bits/stdc++.h>
#define int long long
#define il inline
using namespace std;
namespace asbt{
const int maxn=8e5+5,inf=2e9,mod=998244353;
int n,stk[maxn],top;
struct{
int opt,x;
}a[maxn];
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>n;
for(int i=1,sum=0;i<=n;i++){
cin>>a[i].opt;
if(a[i].opt<=2){
cin>>a[i].x;
if(a[i].opt==2){
sum=min(inf,sum+a[i].x);
}
}else{
a[i].x=sum;
sum=min(sum<<1,inf);
}
}
int num=1,sum=0,ans=0;
for(int i=n;i;i--){
if(a[i].opt==2){
sum=min(inf,sum+a[i].x);
}else if(a[i].opt==3){
if(!a[i].x){
num=(num+num)%mod;
}else if(a[i].x<inf){
stk[++top]=a[i].x;
}
}else{
int d=1,x=a[i].x-sum;
if(x>0){
for(int j=1;j<=top;j++){
if(x>stk[j]){
x-=stk[j];
(d+=1<<(top-j))%=mod;
}
}
ans=(ans+d*1ll*num)%mod;
}
}
}
cout<<ans;
return 0;
}
}
signed main(){return asbt::main();}
E. Polygons
顯然所有多邊形至少公用一個點。又顯然若存在正 \(p\) 邊形,則對于 \(q|p\) 必然存在正 \(q\) 邊形。于是每新加入一個正 \(p\) 邊形,其貢獻為 \(\varphi(p)\)。于是將所有 \(\varphi\) 排個序取前 \(k\) 小的即可。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
using namespace std;
const int maxn=1e6+5;
int n,m,prm[maxn],prn,phi[maxn];
bool npr[maxn];
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>n>>m;
if(m==1){
cout<<3;
return 0;
}
phi[1]=1;
for(int i=2;i<=n;i++){
if(!npr[i]){
prm[++prn]=i;
phi[i]=i-1;
}
for(int j=1;j<=prn&&i*1ll*prm[j]<=n;j++){
npr[i*prm[j]]=1;
if(i%prm[j]==0){
phi[i*prm[j]]=phi[i]*prm[j];
break;
}
phi[i*prm[j]]=phi[i]*phi[prm[j]];
}
}
ll ans=0;
sort(phi+1,phi+n+1);
m+=2;
for(int i=1;i<=m;i++){
ans+=phi[i];
}
cout<<ans;
return 0;
}
F. Minimum Array
區間操作考慮差分。差分后字典序最小的限制即為存在某個位置 \(i\),\(1\) 到 \(i-1\) 的所有前綴和都相同,\(1\) 到 \(i\) 的前綴和更小,也就是差分數組字典序更小。假設之前最小的答案出現在第 \(ans\) 次操作后,第 \(ans+1\) 到當前這一次的操作累加到一起為 \(b\) 序列,當前這次操作后答案更小當且僅當差分數組的第一個非零的位置為負數,用 set 維護即可。
Code
#include<bits/stdc++.h>
#define int long long
#define il inline
using namespace std;
namespace asbt{
const int maxn=5e5+5;
int T,n,m,a[maxn],b[maxn];
set<int> st;
struct{
int l,r,x;
}c[maxn];
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>T;
while(T--){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n+1;i++){
b[i]=0;
}
cin>>m;
int ans=0;
for(int i=1,l,r,x;i<=m;i++){
cin>>l>>r>>x;
c[i]={l,r,x};
if(x){
if(b[l]==0){
st.insert(l);
}
b[l]+=x;
if(b[l]==0){
st.erase(l);
}
if(b[r+1]==0){
st.insert(r+1);
}
b[r+1]-=x;
if(b[r+1]==0){
st.erase(r+1);
}
}
if(st.size()&&b[*st.begin()]<0){
ans=i;
for(int j:st){
b[j]=0;
}
st.clear();
}
}
for(int i:st){
b[i]=0;
}
st.clear();
for(int i=1,l,r,x;i<=ans;i++){
l=c[i].l,r=c[i].r,x=c[i].x;
b[l]+=x,b[r+1]-=x;
}
for(int i=1;i<=n;i++){
b[i]+=b[i-1];
cout<<a[i]+b[i]<<' ';
}
cout<<'\n';
}
return 0;
}
}
signed main(){return asbt::main();}


 浙公網安備 33010602011771號
浙公網安備 33010602011771號