【做題記錄】dp(馬思博)
A. 【模板】動態(tài) DP
好像是我做過的最難的一道 DDP(?)
普通的轉(zhuǎn)移 \(\begin{cases}f_{u,0}=\sum\max(f_{v,0},f_{v,1})\\f_{u,1}=a_u+\sum f_{v,0}\end{cases}\) 是不好優(yōu)化的,我們希望 \(f_{u,0/1}\) 只從一個節(jié)點轉(zhuǎn)移來。不妨設其中一個節(jié)點為 \(v\)(實際上就是重兒子,至于為什么一會兒再說),設 \(g_{u,0}\) 表示不選 \(u\),只考慮輕兒子的最大獨立集,\(g_{u,1}\) 表示選 \(u\),只考慮輕兒子的最大獨立集。于是有新轉(zhuǎn)移 \(\begin{cases}f_{u,0}=g_{u,0}+\max(f_{v,0},f_{v,1})\\f_{u,1}=g_{u,1}+f_{v,0}\end{cases}\)。于是可以用線段樹維護矩陣,由于從下往上轉(zhuǎn)移,矩陣設計為左乘的形式比較方便。每次修改將 \(u\) 的根鏈所有鏈頭的父親的矩陣改變即可。這也就是重剖的原因,保證了時間復雜度線性對數(shù)方。
Code
#include<bits/stdc++.h>
#define int long long
#define il inline
#define pb push_back
#define lid id<<1
#define rid id<<1|1
using namespace std;
namespace asbt{
const int maxn=1e5+5,inf=1e18;
int n,m,a[maxn],sz[maxn],hes[maxn],fa[maxn];
int dfn[maxn],cnt,stk[maxn],top[maxn];
int bot[maxn],f[maxn][2];
vector<int> e[maxn];
struct juz{
int a[2][2];
juz(){
a[0][0]=a[0][1]=a[1][0]=a[1][1]=-inf;
}
il int*operator[](int x){
return a[x];
}
il juz operator*(juz x)const{
juz r;
for(int i:{0,1}){
for(int j:{0,1}){
r[i][j]=max(a[i][0]+x[0][j],a[i][1]+x[1][j]);
}
}
return r;
}
}b[maxn],tr[maxn<<2];
il void dfs1(int u){
sz[u]=1;
int mxs=0;
for(int v:e[u]){
if(v==fa[u]){
continue;
}
fa[v]=u;
dfs1(v);
sz[u]+=sz[v];
if(mxs<sz[v]){
mxs=sz[v],hes[u]=v;
}
}
}
il void dfs2(int u){
if(!top[u]){
top[u]=u;
}
dfn[u]=++cnt,stk[cnt]=u;
bot[top[u]]=u;
if(hes[u]){
top[hes[u]]=top[u];
dfs2(hes[u]);
}
int &g0=b[u][0][0]=0,&g1=b[u][1][0]=a[u];
for(int v:e[u]){
if(v==fa[u]||v==hes[u]){
continue;
}
dfs2(v);
g0+=max(f[v][0],f[v][1]);
g1+=f[v][0];
}
b[u][0][1]=g0;
f[u][0]=0,f[u][1]=a[u];
for(int v:e[u]){
if(v==fa[u]){
continue;
}
f[u][0]+=max(f[v][0],f[v][1]);
f[u][1]+=f[v][0];
}
}
il void pushup(int id){
tr[id]=tr[lid]*tr[rid];
}
il void build(int id,int l,int r){
if(l==r){
tr[id]=b[stk[l]];
return ;
}
int mid=(l+r)>>1;
build(lid,l,mid);
build(rid,mid+1,r);
pushup(id);
}
il void upd(int id,int l,int r,int p){
if(l==r){
tr[id]=b[stk[p]];
return ;
}
int mid=(l+r)>>1;
if(p<=mid){
upd(lid,l,mid,p);
}else{
upd(rid,mid+1,r,p);
}
pushup(id);
}
il juz query(int id,int L,int R,int l,int r){
if(L>=l&&R<=r){
return tr[id];
}
int mid=(L+R)>>1;
if(r<=mid){
return query(lid,L,mid,l,r);
}
if(l>mid){
return query(rid,mid+1,R,l,r);
}
return query(lid,L,mid,l,r)*query(rid,mid+1,R,l,r);
}
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1,u,v;i<n;i++){
cin>>u>>v;
e[u].pb(v),e[v].pb(u);
}
dfs1(1),dfs2(1),build(1,1,n);
// for(int i=1;i<=n;i++){
// cout<<i<<' '<<sz[i]<<' '<<hes[i]<<' '<<dfn[i]<<' '<<top[i]<<' '<<bot[i]<<'\n';
// }
while(m--){
int u,x;
cin>>u>>x;
b[u][1][0]+=x-a[u],a[u]=x;
while(u){
juz p=query(1,1,n,dfn[top[u]],dfn[bot[top[u]]]);
upd(1,1,n,dfn[u]);
juz q=query(1,1,n,dfn[top[u]],dfn[bot[top[u]]]);
u=fa[top[u]];
int &g0=b[u][0][0],&g1=b[u][1][0];
g0-=max(p[0][0],p[1][0]);
g0+=max(q[0][0],q[1][0]);
g1-=p[0][0],g1+=q[0][0];
b[u][0][1]=g0;
}
juz r=query(1,1,n,dfn[1],dfn[bot[1]]);
cout<<max(r[0][0],r[1][0])<<'\n';
}
return 0;
}
}
signed main(){return asbt::main();}
C. [POI 2011] Lightning Conductor
相當于是對于每個 \(i\),求 \(\max\{a_j+\sqrt{i-j}-a_i\}\)。滿足決策單調(diào)性,分治即可。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
using namespace std;
namespace asbt{
const int maxn=5e5+5,inf=1e9;
int n,a[maxn],ans[maxn];
double sq[maxn];
il void solve(int L,int R,int l,int r){
if(l>r){
return ;
}
int mid=(l+r)>>1,p=0;
double v=-inf;
for(int i=L;i<=min(mid,R);i++){
double t=a[i]-a[mid]+sq[mid-i];
if(v<t){
p=i,v=t;
}
}
ans[mid]=max(ans[mid],(int)ceil(v));
solve(L,p,l,mid-1);
solve(p,R,mid+1,r);
}
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
sq[i]=sqrt(i);
}
memset(ans,-0x3f,sizeof(ans));
solve(1,n,1,n);
reverse(a+1,a+n+1);
reverse(ans+1,ans+n+1);
solve(1,n,1,n);
for(int i=n;i;i--){
cout<<max(ans[i],0)<<'\n';
}
return 0;
}
}
int main(){return asbt::main();}
D. [國家集訓隊] Tree I
我們設選了 \(i\) 條白邊時的最小生成樹為 \(f_i\),于是得到了若干個點 \((i,f_i)\)。打表可得,這些點組成了一個下凸包。我們考慮二分斜率 \(k\),找到切點 \((i,f_i)\),當 \(i=need\) 時 \(f_i\) 就是答案。如下圖:
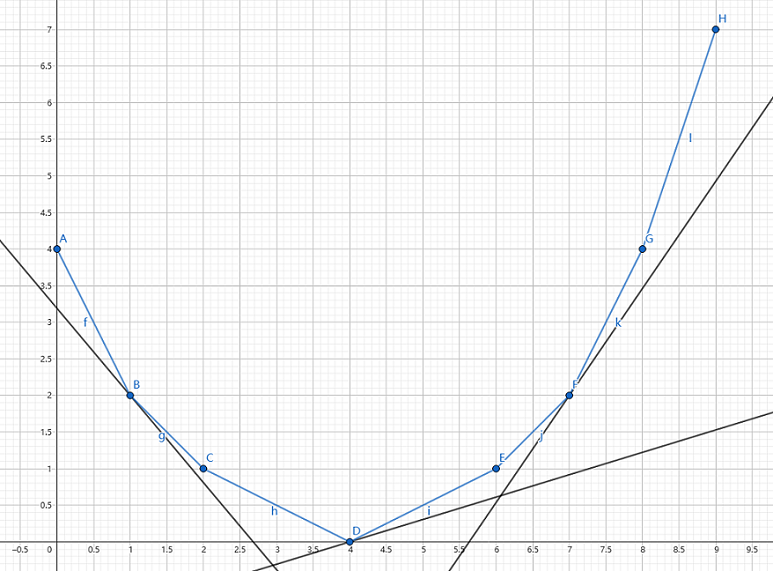
問題轉(zhuǎn)變?yōu)榍笄悬c。容易發(fā)現(xiàn),在所有斜率為 \(k\) 的直線中,切點所在的那一條縱截距最小。如下圖:

那么我們怎么求最小的縱截距呢?設這條直線為 \(y=kx+b\),則有 \(kx+b=f_x\),于是縱截距即為 \(b=f_x-kx\),也就是給每條白邊都減去了 \(k\)。于是我們給白邊減去 \(k\) 再求最小生成樹即可。時間復雜度線性對數(shù)。
實際上,這個算法叫做 wqs 二分。解決這種“欽定選 \(need\) 個物品時的最值”問題時經(jīng)常使用 wqs 二分,它的特點是要求 \(f_i\) 必須是凸函數(shù)、細節(jié)多得像屎。至于本題中的二分上下界,因為凸包的最小/大斜率一定不超過 \([-100,100]\),因此定為 \([-100,100]\) 即可。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
using namespace std;
namespace asbt{
const int maxn=1e5+5;
int n,m,kk,ca,cb,fa[maxn];
struct edge{
int u,v,w,opt;
il bool operator<(const edge &x)const{
return w<x.w;
}
}a[maxn],b[maxn],c[maxn];
il int find(int x){
return x!=fa[x]?fa[x]=find(fa[x]):x;
}
il bool check(int x){
int p1=1,p2=1,p3=1;
while(p1<=ca&&p2<=cb){
if(a[p1].w-x<=b[p2].w){
c[p3++]=a[p1++];
}
else{
c[p3++]=b[p2++];
}
}
while(p1<=ca){
c[p3++]=a[p1++];
}
while(p2<=cb){
c[p3++]=b[p2++];
}
for(int i=0;i<n;i++){
fa[i]=i;
}
int cnt=0;
for(int i=1;i<=m;i++){
int u=find(c[i].u),v=find(c[i].v);
if(u!=v){
fa[u]=v,cnt+=c[i].opt^1;
}
}
return cnt>=kk;
}
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>n>>m>>kk;
for(int i=1,u,v,w,opt;i<=m;i++){
cin>>u>>v>>w>>opt;
if(!opt){
a[++ca]={u,v,w,opt};
}
else{
b[++cb]={u,v,w,opt};
}
}
sort(a+1,a+ca+1),sort(b+1,b+cb+1);
int l=-100,r=100;
while(l<r){
int mid=(l+r)>>1;
if(check(mid)){
r=mid;
}
else{
l=mid+1;
}
}
int p1=1,p2=1,p3=1;
while(p1<=ca&&p2<=cb){
if(a[p1].w-l<=b[p2].w){
c[p3]=a[p1++];
c[p3++].w-=l;
}
else{
c[p3++]=b[p2++];
}
}
while(p1<=ca){
c[p3]=a[p1++];
c[p3++].w-=l;
}
while(p2<=cb){
c[p3++]=b[p2++];
}
for(int i=0;i<n;i++){
fa[i]=i;
}
int ans=0;
for(int i=1;i<=m;i++){
int u=find(c[i].u),v=find(c[i].v);
if(u!=v){
fa[u]=v,ans+=c[i].w;
}
}
cout<<ans+kk*l;
return 0;
}
}
int main(){return asbt::main();}
E. Gosha is hunting
顯然有三維的 DP:設 \(f_{i,j,k}\) 表示考慮到第 \(i\) 個神奇寶貝,用了 \(j\) 個寶貝球和 \(k\) 個超級球的最大期望。可以發(fā)現(xiàn) \(f_{i,j,k}\) 是關于 \(k\) 的上凸包,wqs 二分即可。時間復雜度 \(O(n^2\log V)\)。
LG 上的這篇討論中有相當多的 hack 數(shù)據(jù),非常毒瘤的是那組號稱更小但更強的數(shù)據(jù)是錯的(害得我干瞪著代碼看了十五分鐘。。。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
using namespace std;
namespace asbt{
const int maxn=2e3+5;
const double eps=1e-8;
int n,a,b,g[maxn][maxn];
double p[maxn],q[maxn];
double f[maxn][maxn];
il bool check(double x){
for(int i=1;i<=n;i++){
for(int j=0;j<=a;j++){
f[i][j]=g[i][j]=0;
if(f[i][j]<f[i-1][j]){
f[i][j]=f[i-1][j];
g[i][j]=g[i-1][j];
}
if(j&&f[i][j]<f[i-1][j-1]+p[i]){
f[i][j]=f[i-1][j-1]+p[i];
g[i][j]=g[i-1][j-1];
}
if(f[i][j]<f[i-1][j]+q[i]-x){
f[i][j]=f[i-1][j]+q[i]-x;
g[i][j]=g[i-1][j]+1;
}
if(j&&f[i][j]<f[i-1][j-1]+p[i]+q[i]-x-p[i]*q[i]){
f[i][j]=f[i-1][j-1]+p[i]+q[i]-x-p[i]*q[i];
g[i][j]=g[i-1][j-1]+1;
}
}
}
return g[n][a]<=b;
}
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>n>>a>>b;
for(int i=1;i<=n;i++){
cin>>p[i];
}
for(int i=1;i<=n;i++){
cin>>q[i];
}
double l=0,r=1;
while(r-l>eps){
double mid=(l+r)/2;
if(check(mid)){
r=mid;
}else{
l=mid;
}
}
check(l);
// cout<<l<<' '<<g[n][a]<<'\n';
cout<<fixed<<setprecision(6)<<f[n][a]+l*b;
return 0;
}
}
int main(){return asbt::main();}
H. 小N的獨立集
最大獨立集有一個經(jīng)典 DP:設 \(dp_{i,0/1}\) 表示選/不選 \(i\),\(i\) 的子樹的最大獨立集。因為要求滿足 \(dp_{i,0/1}=x\) 的樹的數(shù)量, 所以考慮 DP 套 DP:設 \(f_{i,j,k}\) 表示 \(dp_{i,0}=j,dp_{i,1}=k\) 的方案數(shù)。但這樣時間空間都是開不下的,考慮修改 DP 數(shù)組的定義,\(dp_{i,0/1}\) 表示強制/不強制不選 \(i\) 的最大獨立集,\(f_{i,j,k}\) 表示 \(dp_{i,0}=j,dp_{i,1}=j+k\) 的方案數(shù),因為 \(k\le5\) 所以直接樹上背包轉(zhuǎn)移即可。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
#define pb push_back
using namespace std;
namespace asbt{
const int maxn=1e3+5,mod=1e9+7;
int n,m,sz[maxn];
ll f[maxn][maxn*5][7],g[maxn*5][7];
vector<int> e[maxn];
il void dfs(int u,int fa){
sz[u]=1;
for(int i=1;i<=m;i++){
f[u][0][i]=1;
}
for(int v:e[u]){
if(v==fa){
continue;
}
dfs(v,u);
for(int i=0;i<=(sz[u]+sz[v])*m;i++){
for(int j=0;j<=m;j++){
g[i][j]=0;
}
}
for(int i1=0;i1<=sz[u]*m;i1++){
for(int j1=0;j1<=m;j1++){
if(!f[u][i1][j1]){
continue;
}
for(int i2=0;i2<=sz[v]*m;i2++){
for(int j2=0;j2<=m;j2++){
if(!f[v][i2][j2]){
continue;
}
(g[i1+i2+j2][max(j1-j2,0)]+=f[u][i1][j1]*f[v][i2][j2])%=mod;
}
}
}
}
sz[u]+=sz[v];
for(int i=0;i<=sz[u]*m;i++){
for(int j=0;j<=m;j++){
f[u][i][j]=g[i][j];
}
}
}
}
int main(){
freopen("nset.out","w",stdout);
freopen("nset.in","r",stdin);
ios::sync_with_stdio(0),cin.tie(0);
cin>>n>>m;
for(int i=1,u,v;i<n;i++){
cin>>u>>v;
e[u].pb(v),e[v].pb(u);
}
dfs(1,0);
for(int i=1;i<=n*m;i++){
ll ans=0;
for(int j=0;j<=min(i,m);j++){
ans+=f[1][i-j][j];
}
cout<<ans%mod<<"\n";
}
return 0;
}
}
int main(){return asbt::main();}
I. [NOI Online #1 入門組] 跑步
問題等價于劃分成若干無序的數(shù),\(O(n^2)\) 的多重背包是顯然的。
考慮根號分治,對于劃分中 \(<\sqrt{n}\) 的數(shù),用多重背包求;對于 \(\ge\sqrt{n}\) 的數(shù),設有 \(i\) 個,和為 \(j\) 的方案數(shù)為 \(g_{j,i}\),于是有 \(g_{j,i}=g_{j-i,i}+g_{j-m,i-1}\),相當于是加入一個 \(m\) 或給每個數(shù)加 \(1\)。最后統(tǒng)計答案即可,時間復雜度 \(O(n\sqrt{n})\)。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
using namespace std;
namespace asbt{
const int maxn=1e5+5;
int n,m,mod,f[maxn],g[maxn][325];
il int pls(int x,int y){
return x+y<mod?x+y:x+y-mod;
}
il int mns(int x,int y){
return x<y?x-y+mod:x-y;
}
il void add(int &x,int y){
x=pls(x,y);
}
il void sub(int &x,int y){
x=mns(x,y);
}
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>n>>mod;
m=sqrt(n)+1;
f[0]=1;
for(int i=1;i<m;i++){
for(int j=i;j<=n;j++){
add(f[j],f[j-i]);
}
}
g[0][0]=1;
for(int i=1;i<m;i++){
for(int j=i;j<=n;j++){
g[j][i]=g[j-i][i];
if(j>=m){
add(g[j][i],g[j-m][i-1]);
}
}
}
int ans=0;
for(int i=0;i<=n;i++){
int sum=0;
for(int j=0;j<m;j++){
add(sum,g[i][j]);
}
ans=(f[n-i]*1ll*sum+ans)%mod;
}
cout<<ans;
return 0;
}
}
int main(){return asbt::main();}
J. [agc001_e]BBQ Hard
\(a_i+b_i+a_j+b_j\choose a_i+b_i\) 其實就等價于從 \((-a_i,-b_i)\) 走到 \((a_j,b_j)\) 的方案數(shù),于是 \(O(n^2)\) DP 即可。需要減去 \(i\) 自己給自己的貢獻,還有 \(i>j\) 的貢獻。
Code
#include<bits/stdc++.h>
#define int long long
#define il inline
using namespace std;
namespace asbt{
const int maxn=2e5+5,maxm=4e3+5,mod=1e9+7,inv2=5e8+4;
int n,a[maxn],b[maxn],fac[maxm<<1],inv[maxm<<1],f[maxm][maxm];
il int qpow(int x,int y=mod-2){
int res=1;
while(y){
if(y&1){
(res*=x)%=mod;
}
(x*=x)%=mod,y>>=1;
}
return res;
}
il void init(int n=8e3){
fac[0]=1;
for(int i=1;i<=n;i++){
fac[i]=fac[i-1]*i%mod;
}
inv[n]=qpow(fac[n]);
for(int i=n;i;i--){
inv[i-1]=inv[i]*i%mod;
}
}
il int C(int x,int y){
if(x<y||y<0){
return 0;
}
return fac[x]*inv[y]%mod*inv[x-y]%mod;
}
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>n;
init();
int ans=0;
for(int i=1;i<=n;i++){
cin>>a[i]>>b[i];
(ans+=mod-C((a[i]+b[i])<<1,a[i]<<1))%=mod;
// cout<<C((a[i]+b[i])<<1,a[i]<<1)<<"\n";
f[2001-a[i]][2001-b[i]]++;
}
for(int i=1;i<=4001;i++){
for(int j=1;j<=4001;j++){
f[i][j]=(f[i][j]+f[i-1][j]+f[i][j-1])%mod;
}
}
for(int i=1;i<=n;i++){
(ans+=f[2001+a[i]][2001+b[i]])%=mod;
// cout<<f[2001+a[i]][2001+b[i]]<<"\n";
}
cout<<ans*inv2%mod;
return 0;
}
}
signed main(){return asbt::main();}
M. [CEOI 2016] kangaroo
問題可以轉(zhuǎn)化為求 \(p_1=s\),\(p_n=t\) 且 \(p_i\) 兩邊同時大于/小于 \(p_i\) 的排列 \(p\) 的個數(shù)。
考慮連續(xù)段 DP,設 \(f_{i,j}\) 表示考慮前 \(i\) 個數(shù),分成了 \(j\) 段的方案數(shù)。轉(zhuǎn)移分兩種:
-
新開一段,\(f_{i,j}\leftarrow(j-[i>s]-[i>t])\times f_{i-1,j-1}\)
-
將兩段連起來,\(f_{i,j}\leftarrow j\times f_{i-1,j+1}\)
注意特判 \(i=s\) 或 \(t\) 的情況。時間復雜度 \(O(n^2)\)。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
using namespace std;
namespace asbt{
const int maxn=2e3+5,mod=1e9+7;
int n,s,t,f[maxn][maxn];
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>n>>s>>t;
f[1][1]=1;
for(int i=2;i<=n;i++){
for(int j=1;j<=i;j++){
if(i==s||i==t){
f[i][j]=(f[i-1][j-1]+f[i-1][j])%mod;
}
else{
f[i][j]=(f[i-1][j-1]*1ll*(j-(i>s)-(i>t))+f[i-1][j+1]*1ll*j)%mod;
}
}
}
cout<<f[n][1];
return 0;
}
}
int main(){return asbt::main();}
N. [CSP-S 2022] 數(shù)據(jù)傳輸
對 \(K\) 分討。
\(K=1\),直接倍增求和即可。
\(K=2\),考慮將路徑拉出來 DP。設 \(f_i\) 表示走到第 \(i\) 個點的最小花費。故有 \(f_i=\min(f_{i-1},f_{i-2})+a_i\)。考慮 DDP,可以構造出轉(zhuǎn)移矩陣:
\(K=3\),此時我們發(fā)現(xiàn)可以走到路徑上某個點的某個相鄰點來減小花費。如下圖:

可以發(fā)現(xiàn)每個點掛的點要么是相鄰的最小值,要么就不掛點。記這個掛的點為 \(b_i\)。類似地仍然考慮 DP。設 \(f_{i,0/1}\) 表示走到 \(i\)/\(i\) 掛的點所需的最小花費。于是有轉(zhuǎn)移:
但是這個東西如果用矩陣優(yōu)化,代碼會帶上 \(125\) 的常數(shù)。考慮換個定義。發(fā)現(xiàn) DP 轉(zhuǎn)移只和到 \(i\) 的距離有關,所以設 \(f_{i,0/1/2}\) 表示走到到 \(i\) 的距離為 \(0/1/2\) 的點的最小花費,于是有轉(zhuǎn)移:
進而可以設計出轉(zhuǎn)移矩陣:
于是倍增即可,時間復雜度 \(O(n\log n)\)。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
#define pb push_back
using namespace std;
namespace asbt{
const int maxn=2e5+5;
const ll inf=1e18;
int n,m,kk,anc[maxn][18],dep[maxn];
ll a[maxn],b[maxn];
vector<int> e[maxn];
struct juz{
ll mat[4][4];
juz(bool x=false){
for(int i=1;i<=kk;i++){
for(int j=1;j<=kk;j++){
mat[i][j]=inf;
}
}
if(x){
for(int i=1;i<=kk;i++){
mat[i][i]=0;
}
}
}
juz(int x){
switch(kk){
case 1:{
mat[1][1]=a[x];
break;
}
case 2:{
mat[1][1]=mat[2][1]=a[x];
mat[1][2]=0,mat[2][2]=inf;
break;
}
default:{
mat[1][1]=mat[2][1]=mat[3][1]=a[x];
mat[1][2]=mat[2][3]=0;
mat[1][3]=mat[3][3]=inf;
mat[2][2]=b[x],mat[3][2]=a[x]+b[x];
break;
}
}
}
il ll*operator[](int x){
return mat[x];
}
il juz operator*(juz x)const{
juz res;
for(int i=1;i<=kk;i++){
for(int j=1;j<=kk;j++){
for(int k=1;k<=kk;k++){
res[i][j]=min(res[i][j],mat[i][k]+x[k][j]);
}
}
}
return res;
}
}up[maxn][18],dw[maxn][18];
il void dfs1(int u,int fa){
b[u]=inf;
for(int v:e[u]){
b[u]=min(b[u],a[v]);
if(v==fa){
continue;
}
dfs1(v,u);
}
}
il void dfs2(int u,int fa){
anc[u][0]=fa,dep[u]=dep[fa]+1;
up[u][0]=dw[u][0]=juz(u);
for(int i=1;i<=17;i++){
anc[u][i]=anc[anc[u][i-1]][i-1];
up[u][i]=up[u][i-1]*up[anc[u][i-1]][i-1];
dw[u][i]=dw[anc[u][i-1]][i-1]*dw[u][i-1];
}
for(int v:e[u]){
if(v==fa){
continue;
}
dfs2(v,u);
}
}
il juz dp(int u,int v){
juz resu,resv(true);
if(dep[u]==dep[v]){
resv=dw[v][0],v=anc[v][0];
}
else if(dep[u]<dep[v]){
swap(u,v);
}
resu[1][1]=a[u],u=anc[u][0];
int ddep=dep[u]-dep[v],d=0;
// if(!m){
// cout<<"kpo "<<ddep<<"\n";
// }
while(ddep){
if(ddep&1){
resu=resu*up[u][d];
u=anc[u][d];
}
ddep>>=1,d++;
}
if(u==v){
return resu*up[u][0]*resv;
}
for(int i=17;~i;i--){
if(anc[u][i]!=anc[v][i]){
resu=resu*up[u][i];
resv=dw[v][i]*resv;
u=anc[u][i],v=anc[v][i];
}
}
return resu*up[u][1]*dw[v][0]*resv;
}
int main(){
// freopen("P8820_1.in","r",stdin);
ios::sync_with_stdio(0),cin.tie(0);
cin>>n>>m>>kk;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1,u,v;i<n;i++){
cin>>u>>v;
e[u].pb(v),e[v].pb(u);
}
dfs1(1,0),dfs2(1,0);
while(m--){
int u,v;
cin>>u>>v;
cout<<dp(u,v)[1][1]<<"\n";
}
return 0;
}
}
int main(){return asbt::main();}
O. [NOI2009] 詩人小G
設 \(dp_i\) 表示考慮到 \(i\) 的最小不協(xié)調(diào)度,則有方程:
后面那個東西滿足四邊形不等式,因此可以決策單調(diào)性優(yōu)化。維護決策點隊列,二分出每個決策點可以作為最優(yōu)決策點的范圍即可轉(zhuǎn)移。時間復雜度線性對數(shù)。需要 long double。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
#define ld long double
using namespace std;
namespace asbt{
const int maxn=1e5+5;
const ld inf=1e18;
int T,n,m,kk,a[maxn],pre[maxn],q[maxn];
ld dp[maxn];
string s[maxn];
il ld qpow(ld x,int y){
ld res=1;
while(y){
if(y&1){
res*=x;
}
x*=x,y>>=1;
}
return res;
}
il ld calc(int x,int y){
return dp[x]+qpow(abs(a[y]-a[x]+y-x-1-m),kk);
}
il int find(int x,int y){
int l=y,r=n+1;
while(l<r){
int mid=(l+r)>>1;
if(calc(x,mid)>=calc(y,mid)){
r=mid;
}
else{
l=mid+1;
}
}
return l;
}
il void print(int x){
if(!x){
return ;
}
print(pre[x]);
for(int i=pre[x]+1;i<x;i++){
cout<<s[i]<<" ";
}
cout<<s[x]<<"\n";
}
il void solve(){
cin>>n>>m>>kk;
for(int i=1;i<=n;i++){
cin>>s[i];
a[i]=a[i-1]+s[i].size();
dp[i]=inf,pre[i]=0;
}
int hd=1,tl=0;
dp[0]=0,q[++tl]=0;
for(int i=1;i<=n;i++){
while(hd<tl&&find(q[hd],q[hd+1])<=i){
hd++;
}
dp[i]=calc(q[hd],i),pre[i]=q[hd];
while(hd<tl&&find(q[tl-1],q[tl])>=find(q[tl],i)){
tl--;
}
q[++tl]=i;
}
if(dp[n]>inf){
cout<<"Too hard to arrange\n";
}
else{
cout<<(ll)dp[n]<<"\n";
print(n);
}
cout<<"--------------------\n";
}
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>T;
while(T--){
solve();
}
return 0;
}
}
int main(){return asbt::main();}
P. 忘情
設 \(dp_{i,j}\) 表示到 \(i\) 分了 \(j\) 段的最小值,于是有轉(zhuǎn)移:
發(fā)現(xiàn) \(dp_{i,j}\) 關于 \(j\) 是一個下凸函數(shù),于是可以 wqs 二分。注意為了使截距更小,在截到 \(m\) 點時要繼續(xù)讓斜率變大。
于是內(nèi)層 DP 是這樣一個東西:設 \(f_i\) 為考慮到 \(i\) 的答案,有 \(f_i=\min\limits_{j=0}^{i-1}\{f_j+(sum_i-sum_j+1)^2-k\}\)。化簡得 \(f_j+s_j^2-2s_j=2s_is_j+f_i-s_i^2-2s_i-1+k\)。于是有 \(k_i=2s_i\),\(b_i=f_i-s_i^2-2s_i-1+k\),\(x_j=s_j\),\(y_j=f_j+s_j^2-2s_j\)。因為是最小值,我們用單調(diào)隊列維護 \(j\) 組成的下凸包,用斜率為 \(2s_i\) 的直線去切這個下凸包,斜率優(yōu)化 DP 即可。
Code
#include<bits/stdc++.h>
#define int long long
#define il inline
using namespace std;
namespace asbt{
const int maxn=1e5+5;
int n,m,a[maxn],f[maxn],g[maxn],q[maxn];
il bool check(int x){
int hd=1,tl=0;
f[0]=0,q[++tl]=0;
#define X(i) (a[i])
#define Y(i) (f[i]+a[i]*a[i]-2*a[i])
#define K(i,j) ((Y(j)-Y(i))*1.0l/(X(j)-X(i)))
for(int i=1;i<=n;i++){
while(hd<tl&&K(q[hd],q[hd+1])<2*a[i]){
hd++;
}
f[i]=f[q[hd]]+(a[i]-a[q[hd]]+1)*(a[i]-a[q[hd]]+1)-x;
g[i]=g[q[hd]]+1;
while(hd<tl&&K(q[tl-1],q[tl])>K(q[tl],i)){
tl--;
}
q[++tl]=i;
}
#undef X
#undef Y
#undef K
return g[n]<=m;
}
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
a[i]+=a[i-1];
}
int l=-2e16,r=0;
while(l<r){
int mid=(l+r+1)>>1;
if(check(mid)){
l=mid;
}
else{
r=mid-1;
}
}
check(l);
cout<<f[n]+m*l;
return 0;
}
}
signed main(){return asbt::main();}
Q. [ICPC 2018 WF] Gem Island
首先考慮每一種情況的概率。設最后每個人的寶石數(shù)為 \(c_i\),于是方案數(shù)為 \(\prod\limits_{i=1}^{n}{d-\sum_{j=1}^{i-1}(c_j-1)\choose(c_i-1)}\times\prod\limits_{i=1}^{n}(c_i-1)!=d!\)。于是每種情況的概率都是一樣的,我們只需 DP 出方案數(shù)和總和即可。
先不考慮最開始那 \(n\) 個寶石。設 \(f_{i,j}\) 表示當前共有 \(i\) 個寶石,擁有最多寶石的人有 \(j\) 個時的方案數(shù),于是有轉(zhuǎn)移方程:
類似地,設 \(g_{i,j}\) 表示此時前 \(r\) 大的總和,于是有方程:
答案即為 \(\frac{\sum_{i=1}^{n}f_{d,i}}{\sum_{i=1}^{n}g_{d,i}}\)。時間復雜度 \(O(n^3)\)。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
using namespace std;
namespace asbt{
const int maxn=1e3+5;
int n,d,r;
double f[maxn][maxn],g[maxn][maxn],C[maxn][maxn];;
il void init(int n=1e3){
C[0][0]=1;
for(int i=1;i<=n;i++){
C[i][0]=1;
for(int j=1;j<=i;j++){
C[i][j]=C[i-1][j-1]+C[i-1][j];
}
}
}
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>n>>d>>r;
init();
f[0][n]=1;
for(int i=0;i<=d;i++){
for(int j=1;j<=n;j++){
for(int k=1;k<=j;k++){
f[i+k][k]+=f[i][j]*C[j][k];
g[i+k][k]+=(g[i][j]+min(k,r)*f[i][j])*C[j][k];
}
}
}
double sg=0,sf=0;
for(int i=1;i<=n;i++){
sg+=g[d][i],sf+=f[d][i];
}
cout<<fixed<<setprecision(7)<<sg/sf+r;
return 0;
}
}
int main(){return asbt::main();}
S. [JOI Open 2016] 摩天大樓 / Skyscraper
首先將 \(a\) 排序,然后可以連續(xù)段 DP,設 \(f_{i,j,k,d}\) 表示前 \(i\) 個數(shù)連成 \(j\) 段,和為 \(k\),當前確定了 \(d\) 個邊界的方案數(shù)。
一個比較直觀的費用提前計算是,在插入每個數(shù)時預先算出比它大的數(shù)放在它旁邊時它自己的貢獻。舉個例子,對于另成一段而不貼邊界的轉(zhuǎn)移,有:
其他轉(zhuǎn)移是類似的。這樣的時空復雜度是無法接受的,因為轉(zhuǎn)移過程中 \(k\) 有增有減,雖然最后我們統(tǒng)計答案時只需要 \(k\in[0,L]\) 的貢獻,轉(zhuǎn)移過程中確是無法舍去一些 \(k\) 較大的狀態(tài)的。我們希望換一種貢獻的計算方法,使得轉(zhuǎn)移過程中 \(k\) 只增不減。
考慮排序后的 \(a\) 數(shù)組中的相鄰兩項 \(a_i\) 和 \(a_{i+1}\) 的貢獻,它們的貢獻即為 \((a_{i+1}-a_i)\times cnt_i\),其中 \(cnt_i\) 為覆蓋了 \(a_i\) 到 \(a_{i+1}\) 這一段的最終在題目所求排列里相鄰的數(shù)對數(shù)量。考慮插入 \(a_{i+1}\),此時會對 \(cnt_i\) 產(chǎn)生貢獻。因為插入 \(a_{i+1}\) 之前每一段的兩端的數(shù)都 \(<a_{i+1}\),后面插入的數(shù)都 \(>a_{i+1}\),所以會產(chǎn)生的貢獻就是 \(cnt_i=2j-d\)。于是新的貢獻和 \(k'=k+(a_{i+1}-a_i)(2j-d)\)。于是就可以 DP 了,時間復雜度 \(O(n^2L)\)。
Code
#include<bits/stdc++.h>
#define ll long long
#define il inline
using namespace std;
namespace asbt{
const int mod=1e9+7;
int n,m,a[105],f[105][105][1005][3];
int main(){
ios::sync_with_stdio(0),cin.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
}
if(n==1){
cout<<1;
return 0;
}
sort(a+1,a+n+1);
f[0][0][0][0]=1;
for(int i=0;i<n;i++){
for(int j=0;j<=i;j++){
for(int k=0;k<=m;k++){
for(int d=0;d<=2;d++){
int p=k+(a[i+1]-a[i])*(2*j-d),t=f[i][j][k][d];
if(!t||p>m){
continue;
}
f[i+1][j+1][p][d]=(f[i+1][j+1][p][d]+t*1ll*(j+1-d))%mod;
if(d<2){
f[i+1][j+1][p][d+1]=(f[i+1][j+1][p][d+1]+t*1ll*(2-d))%mod;
}
if(j){
f[i+1][j][p][d]=(f[i+1][j][p][d]+t*1ll*(2*j-d))%mod;
}
if(j&&d<2){
f[i+1][j][p][d+1]=(f[i+1][j][p][d+1]+t*1ll*(2-d))%mod;
}
if(j>=2){
f[i+1][j-1][p][d]=(f[i+1][j-1][p][d]+t*1ll*(j-1))%mod;
}
}
}
}
}
int ans=0;
for(int i=0;i<=m;i++){
(ans+=f[n][1][i][2])%=mod;
}
cout<<ans;
return 0;
}
}
int main(){return asbt::main();}


 浙公網(wǎng)安備 33010602011771號
浙公網(wǎng)安備 33010602011771號