背景與原理：

BP神經網絡通常指基于誤差反向傳播算法的多層神經網絡，BP算法由信號的前向傳播和反向傳播兩個過程組成，在前向傳播的過程中，輸入從輸入層進入網絡，經過隱含層逐層傳遞到達輸出層輸出，如果輸出結果與預期不符那么轉至誤差反向傳播過程，否則結束學習過程。在反向傳播過程中，誤差會基于梯度下降原理分配給各層神經元，修正各個神經元的權值。

考慮一個經典的分類問題，假設我們有一組數據形如$(x_{1},...,x_{n},y)$，其中$y$為這個數據所屬的類別，不妨設有$k$個取值$(C_{1},...,C_{k})$，那么重復之前的描述：我們實際上要求的是給定了一個輸入$X$，求這個輸入屬于某一類的概率，也就是說我們可以理解為輸入一個$n$維向量，希望預測一個$k$維向量，每一維表示這個輸入屬于這一類的概率，而最后我們的預測結果就是概率最大的那一個維度。

考慮一個基礎的邏輯回歸，我們構造了一個線性函數$z=w^{T}x+b$，然后令$g(z)=\dfrac{1}{1+e^{-z}}$，這樣$g(z)$就可以用來表示一個0-1二分類問題中屬于類別1的概率。

而這個函數的意義，一方面在于將$R$光滑對稱地映射到了$(0,1)$區間能有效地表示概率，另一方面，linear的東西始終只是linear的，當然我們可以引入多項式特征解決一定的問題，但這樣我們要面對的問題就是——究竟引入多少才算合適？而這個sigmoid函數能夠把linear的東西變成non-linear的，這就是一個進步。

而如果從神經網絡的生物學背景來看，我們會看到一個神經元一般有兩個狀態，即靜息狀態和興奮狀態，而我們的人工神經網絡從背景上來說是對人類神經系統行為的一種模擬，因此一個取值在$[0,1]$之間的函數可以看做神經元狀態的一個反映——0代表靜息狀態，1代表興奮狀態，所以在神經網絡中，類似于sigmoid這樣的函數是很常用的，它們被稱作激活函數。

那么說了這么多，神經網絡究竟是在干什么呢？

從一定的意義上來說，神經網絡實際上實現的是函數的不斷復合——雖然即使引入了一個sigmoid函數，linear的東西可能還是無法擺脫linear，那我們就再設法復合上一層，這樣它就沒有那么linear了，以此類推，當我們復合次數足夠多的時候，我們得到的最終結果將能夠擬合出這個“客觀正確”的預測模型。

這個過程是怎么實現的呢？

首先神經網絡被分為三個部分：輸入層、隱藏層和輸出層，每層有若干個節點，每個節點稱為一個神經元，輸入層有$n$個節點，對應于輸入特征的維度，輸出層有$k$個節點，對應于要預測的東西的維度。

而我們首先從單隱藏層的結構開始：假設我們只有一個隱藏層，這個隱藏層上有$n_{1}$個節點，那么第$i$個節點要處理的輸入上一層的所有輸入，對于這第一個隱藏層就是$x_{1},...,x_{n}$，而后計算出$z_{i}=w_{i}^{T}x+b$（即輸入的一個線性函數），然后用自己的激活函數處理這個信號并發出，即第$i$個節點的輸出是$f_{i}(z_{i})$

那么這個過程實際上就是對人類神經元活動的一種模擬：神經元接受上一個神經元發來的信號——神經元處理信號產生一個神經沖動傳遞給下一個神經元

那么我們假設只有一個隱藏層，那么這個隱藏層的輸出就是$f_{1}(z_{1}),...,f_{n_{1}}(z_{n_{1}})$，而下一個就到了輸出層，即輸出層的第$j$個神經元輸出的就是$f_w0obha2h00(\omega_{j}^{T}f(z)+\beta_{j})$（無需在意符號，只是為了區分各個層的參數）

那么非常自然地，如果我們有很多個隱藏層，對于第二個隱藏層而言，其接受的輸入就是第一個隱藏層的輸出，以此類推，每個神經元還是按照自己的參數將上一層的輸出線性組合后扔進自己的激活函數里輸出給下一層，直到到達輸出層為止。

那么實際上，對于一個全連接神經網絡，假設上一層有$n$個神經元，下一層有$m$個神經元，上一層第$j$個神經元的輸出是$a_{j}$，那么下一層第$i$個神經元的輸入是$\sum_{j=1}^{n}w_{ij}a_{j}+b_{i}$

那么如果設下一層是第$d$層，上一層是第$d-1$層，這樣下一層的輸入是上一層的輸出的一個線性組合，記為$z_w0obha2h00$，我們有：

$z_w0obha2h00=\begin{pmatrix} z_{1} \\ z_{2} \\ ... \\ z_{m} \end{pmatrix}=\begin{pmatrix} \sum_{j=1}^{n}w_{1j}a_{j}+b_{1} \\ \sum_{j=1}^{n}w_{2j}a_{j}+b_{2} \\ ... \\ \sum_{j=1}^{n}w_{mj}a_{j}+b_{m} \end{pmatrix}=\begin{pmatrix} w_{11} & w_{12} & ... & w_{1n} \\ w_{21} & w_{22} &.. & w_{2n}\\...\\w_{m1} & w_{m2} &...& w_{mn}\end{pmatrix} \begin{pmatrix} a_{1}\\a_{2}\\...\\a_{n} \end{pmatrix} + \begin{pmatrix} b_{1}\\b_{2} \\...\\b_{m}\end{pmatrix}$

 這樣我們設$W_w0obha2h00=\begin{pmatrix} w_{11} & w_{12} & ... & w_{1n} \\ w_{21} & w_{22} &.. & w_{2n}\\...\\w_{m1} & w_{m2} &...& w_{mn}\end{pmatrix}$，而$a_{d-1}=\begin{pmatrix} a_{1}\\a_{2}\\...\\a_{n} \end{pmatrix}$，$b_w0obha2h00=\begin{pmatrix} b_{1}\\b_{2} \\...\\b_{m}\end{pmatrix}$

這樣我們有$z_w0obha2h00=W_w0obha2h00a_w0obha2h00+b_w0obha2h00$，而第$d$層的輸出，也即第$d+1$層的輸入就是$a_w0obha2h00=f_w0obha2h00(z_w0obha2h00)$

這樣的就構成了一個神經網絡，如果每一個神經元的激活函數選的足夠好，參數也訓練的足夠好，再忽略可能的過擬合問題，那么這個神經網絡的表現應該是很不錯的。

但是...等等，這樣的神經網絡要怎么訓練啊！

這個問題是巨大的——假設我們的神經網絡每層有10個神經元，而我們一共有10個隱藏層，這樣就需要100個神經元，而每個神經元要對前一層10個神經元的輸出做一個線性組合，這就需要11個參數，也就是說這樣一個“簡陋”的神經網絡我們就要訓練足足1100個參數（粗略估計，并不嚴格）！

那么如果沒有一個合適的方法，訓練神經網絡的開銷將是災難性的。

幸運的是，回憶一開始的梯度下降方法，我們知道如果我們希望讓一個函數盡快到達最低點，我們只需按照一定的步長沿下降最快的方向前進即可，那么在這里是不是也可以引入類似的方法呢？

在神經網絡中我們需要的參數主要有$w,b$，那么我們定義一個損失函數$J(w,b)$，那如果我們能求出一個梯度$\dfrac{\partial J}{\partial w_{i}}$，那我們當然可以按照梯度下降的方法更新$\hat{w_{i}}=w_{i}-\alpha \dfrac{\partial J}{\partial w_{i}}$

但是很遺憾的是，由于函數復合的復雜性，我們想要計算出一個損失函數對某個具體的$w_{i}$的偏導數是相當困難的，因為這個$w_{i}$可能前面復合了一堆東西，后面又復合上了一堆東西，想要直接計算出這個偏導數是另一場災難。

幸運的是，我們可以從另一個角度來思考這個問題：我們從輸出層向前來考慮，假設輸出為一個列向量$a_{D}$，而這個$a_{D}$滿足$a_{D}=f_{D}(w_{D}a_{D-1}+b_{D})$，那么我們可以很自然地看到：

$\dfrac{\partial J}{\partial w_{D}}=\dfrac{\partial J}{\partial z_{D}} \dfrac{\partial z_{D}}{\partial w_{D}}=\dfrac{\partial J}{\partial z_{D}} a_{D-1}$

$\dfrac{\partial J}{\partial b_{D}}=\dfrac{\partial J}{\partial z_{D}} \dfrac{\partial z_{D}}{\partial b_{D}}=\dfrac{\partial J}{\partial z_{D}} $

而$a_{D-1}$是已知，我們實際要求出：

$\dfrac{\partial J}{\partial z_{D}}$

當然，這個是不難求解的，求解的結果與損失函數有關，我們不妨設這個東西是$\delta_{D}=\dfrac{\partial J}{\partial z_{D}}$

那我們再往前求，如果我們想求出$\dfrac{\partial J}{\partial w_w0obha2h00}$，那么由復合函數求導法則，我們有：

$\dfrac{\partial J}{\partial w_w0obha2h00}=\dfrac{\partial J}{\partial z_{D}}\dfrac{\partial z_{D}}{\partial z_{D-1}}...\dfrac{\partial z_{d+1}}{\partial z_w0obha2h00}\dfrac{\partial z_w0obha2h00}{\partial w_w0obha2h00}$

而我們知道$\dfrac{\partial z_w0obha2h00}{\partial w_w0obha2h00}=a_{d-1}$，因此我們有：

$\dfrac{\partial J}{\partial w_w0obha2h00}=\dfrac{\partial J}{\partial z_{D}}\dfrac{\partial z_{D}}{\partial z_{D-1}}...\dfrac{\partial z_{d+1}}{\partial z_w0obha2h00}a_{d-1}$

這樣我們設$\delta_w0obha2h00=\dfrac{\partial J}{\partial z_w0obha2h00}$，那么我們始終有：

$\dfrac{\partial J}{\partial w_w0obha2h00}=\delta_w0obha2h00 a_{d-1}$

而$\delta_w0obha2h00=\dfrac{\partial J}{\partial z_{D}}\dfrac{\partial z_{D}}{\partial z_{D-1}}...\dfrac{\partial z_{d+1}}{\partial z_w0obha2h00}$，那么我們有遞推：

$\delta_w0obha2h00=\delta_{d+1}\dfrac{\partial z_{d+1}}{\partial z_w0obha2h00}$

而我們需要算出的是$\dfrac{\partial z_{d+1}}{\partial z_w0obha2h00}$

而我們知道$z_{d+1}=w_{d+1}f(z_w0obha2h00)+b_{d+1}$，這樣我們有：

$\dfrac{\partial z_{d+1}}{\partial z_w0obha2h00}=\dfrac{\partial z_{d+1}}{\partial f_w0obha2h00(z_w0obha2h00)}\dfrac{\partial f_w0obha2h00(z_w0obha2h00)}{\partial z_w0obha2h00}$

因此我們最后得到：

$\dfrac{\partial z_{d+1}}{\partial z_w0obha2h00}=w_{d+1}f_w0obha2h00^{'}(z_w0obha2h00)$

因此我們得知：當前層的梯度應該等于回傳回當前層的梯度（$\delta_{d+1}$）乘以當前層的導數再乘以上一層的輸入。

那么我們總結一下BP神經網絡的流程：

首先要確定輸入、輸出和損失函數，然后選取神經網絡的結構（層數、每層的神經元個數、每層的激活函數、學習率），然后按照上述過程訓練至收斂就好。

代碼實現：

import numpy as np
from sklearn import datasets
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import LinearSVC
import matplotlib.pyplot as plt
import pylab as plt
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
import tensorflow as tf
from sklearn.neural_network import MLPClassifier


X,y=datasets.make_classification(n_samples=1000,n_features=20,n_informative=2,n_redundant=2)
X_train,X_test,Y_train,Y_test=train_test_split(X,y,test_size=0.25)

lr=LogisticRegression()
svc=LinearSVC(C=1.0)
rfc=RandomForestClassifier(n_estimators=100)#森林中樹的個數

lr=lr.fit(X_train,Y_train)
score1=lr.score(X_test,Y_test)
print(score1)

svc=svc.fit(X_train,Y_train)
score2=svc.score(X_test,Y_test)
print(score2)

rfc=rfc.fit(X_train,Y_train)
score3=rfc.score(X_test,Y_test)
print(score3)

gnb=GaussianNB()
gnb=gnb.fit(X_train,Y_train)
score4=gnb.score(X_test,Y_test)
print(score4)


sc=[]
siz=[]
i=5
while i<=100:
    clf = MLPClassifier(solver='lbfgs', alpha=1e-5,activation='logistic',
                    hidden_layer_sizes=(i,i), random_state=1,max_iter=500000)
    clf.fit(X_train, Y_train)
    sc.append(clf.score(X_test,Y_test))
    siz.append(i)
    i+=5
plt.plot(siz,sc,c='r')
plt.show()

這段代碼使用sklearn自帶的簡易神經網絡分類器來訓練一個模型，其中solver這個參數指定了梯度下降的方式，alpha指定了正則化參數，activation指定了激活函數，hidden_layer_sizes是一個元組，每一項對應于一個隱藏層中神經元的個數，max_iter決定了神經網絡最大的迭代次數，超過這個次數的話會返回一個錯誤

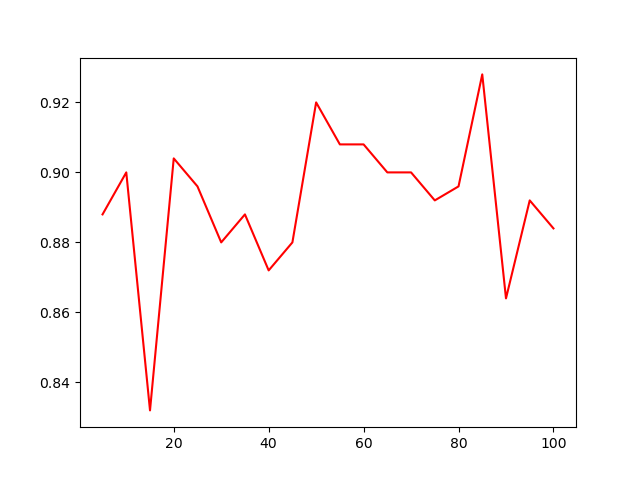
這是這個兩個隱藏層的神經網絡在這組數據上的表現隨每層神經元個數變化的圖像

import numpy as np
from sklearn import datasets
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import LinearSVC
import matplotlib.pyplot as plt
import pylab as plt
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
from sklearn.neural_network import MLPClassifier


X,y=datasets.make_classification(n_samples=1000,n_features=20,n_informative=2,n_redundant=2)
X_train,X_test,Y_train,Y_test=train_test_split(X,y,test_size=0.25)

Y_train=np.array(Y_train).reshape(750,1)
Y_test=np.array(Y_test).reshape(250,1)

def add_layer(input, in_size, out_size, activation_function=None):
    w = tf.Variable(tf.random_normal([in_size, out_size]))
    b = tf.Variable(tf.zeros([1, out_size]) + 0.1)
    Z = tf.matmul(input, w) + b
    if activation_function == None:
        output = Z
    else:
        output = activation_function(Z)
    return output


xs = tf.compat.v1.placeholder(tf.float32, [None, 20])
ys = tf.compat.v1.placeholder(tf.float32, [None, 1])


hidden_layer1 = add_layer(xs, 20, 10, activation_function=tf.nn.relu)
hidden_layer2 = add_layer(hidden_layer1,10,10,activation_function=tf.nn.relu)

prediction = add_layer(hidden_layer2, 10, 1, activation_function=None)


loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys - prediction), reduction_indices=[1]))

train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss)

init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
for i in range(1000):
    sess.run(train_step, feed_dict={xs: X_train, ys: Y_train})
    if i % 100 == 0:
        print(sess.run(loss, feed_dict={xs: X_test, ys: Y_test}))

sess.close()

這是用tensorflow搭建神經網絡的一個方法，首先我們需要自定義一個函數叫做add_layer，這個函數輸入的參數是而上一層是誰，上一層的神經元個數，本層神經元個數，和本層的激活函數

而每層的初始值可以設成隨機值，這里的$w$設計成了一個矩陣，因為對于上一層的第$i$個神經元和本層的第$j$個神經元而言對應的$w$值其實就是$w_{ij}$，而如果我們把一整層看做一個向量的話那么兩層之間的線性變換過程實際就是一個矩陣乘法，最后根據激活函數進行下激活就完成了這一層的任務。

而初始我們需要定義兩個占位符xs和ys表示輸入和輸出，第一維是None，第二維表示維度

接下來我們可以定義一些隱藏層和一個輸出層，以及一個損失函數，這里按照參考格式寫就好。

而反向傳播的過程不需要我們來寫，TensorFlow提供一個train的包，可以決定按什么方法進行優化，而參數是學習率，后面的minimize是我們要最小化的那個損失函數。

最后我們用tensorflow里的一個叫Session的對象run這個神經網絡，就可以實現訓練的功能了。

小結與提高：

反向傳播神經網絡是最簡單的神經網絡，在很多任務上表現優越，但其也有很多問題，比如模型的可解釋性很差——事實上整個神經網絡雖然原理清晰，但真實過程就像一個黑盒，比如上面我們會看到模型的表現隨神經元個數在震蕩，這樣的現象并不容易找到一個簡單的解釋。同時由于超參數很多，如何選取就成了一個大問題，同時由于模型的復雜性導致很容易出現過擬合的現象，同時模型的復雜還會帶來訓練成本的大幅上升，這些都是神經網絡所要面對的大問題。