原題鏈接

解析

先考慮 \(K = 1\) 的情況，加一條邊會連出一個環，環上所有邊只需經過 \(1\) 次，這個可以利用無向圖歐拉回路的判定來證明。巡邏距離最小就是要讓環盡量大，所以連直徑端點即可。

再來看 \(K = 2\)，由于有公共邊的存在，兩個環的貢獻無法通過直接相加來計算。畫個圖發現一般情況下公共邊必定走兩次，非一般情況是有葉子連了兩條邊，這樣可能公共邊只走一次，然后走兩遍環的另一側會更優，但是這樣必定不優于把其中一條邊在該葉子處斷開然后連回到點 \(1\)，所以我們只用考慮公共邊走兩次的情況。

考慮在定了一條路徑的情況下如何去定第二條路徑。考慮貢獻，初始答案為 \(2n - 1\)，環上每條非公共邊對答案做額外 \(-1\) 的貢獻，公共邊額外做 \(0\) 的貢獻。所以，將在第一個環上的所有邊邊權置 \(1\)，其余邊置 \(-1\)，問題就變成了找到樹上邊權最小的一條簡單路徑，按類似求直徑的方法 dp 來求即可。為什么要置 \(1\) 而不是置 \(0\)？因為走公共邊相當于把第一個環 \(-1\) 的貢獻給抵消了。

那么第一條路徑應該選誰呢？第一想到的肯定是直徑，我們來嘗試證明一下這么做是最優的：

首先欽定第一條路徑的長度不小于第二條。

設路徑 \(L=a \to b\) 是直徑。

如果有一種更優的選法，第一條路徑選了 \(l=u \to v \not= L\)，那么 \(l\) 需要與直徑有公共邊，否則直接選直徑和 \(l\) 必定不劣。同理，第二條邊 \(l_2=u_2 \to v_2\) 也需要跟直徑 \(L\) 有公共邊，且在長度相同的情況下， \(l_2\) 跟 \(l\) 有公共邊的情況必定不優于沒有公共邊的情況。所以只需要考慮如圖所示的這種情況：

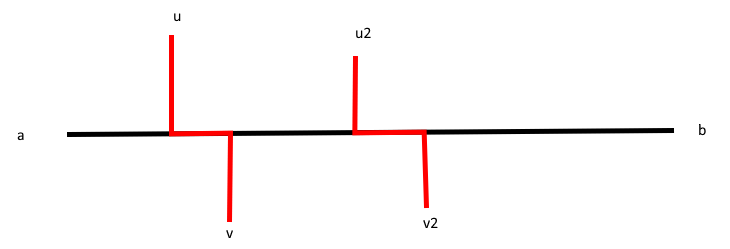
此時如果我們選取直徑 \(L\) 和 \(u_2 \to v\) 作為兩條路徑：

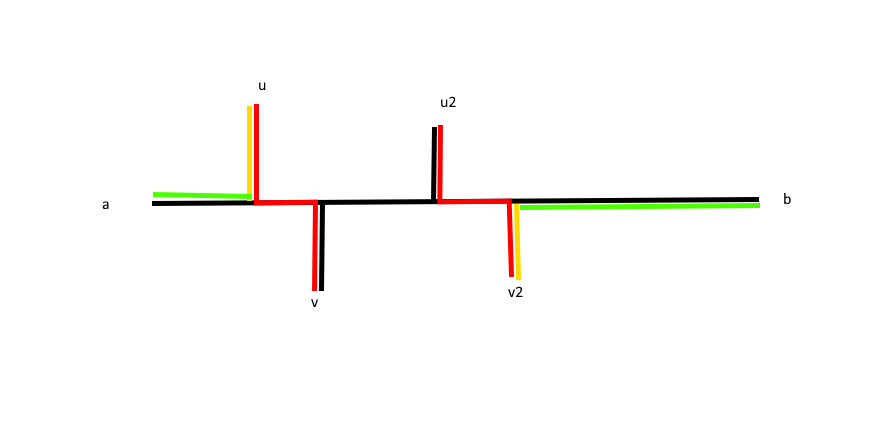
去除共有的部分后，比較綠色部分和黃色部分，顯然黃色部分不可能長于綠色部分，不然 \(a \to b\) 就不是直徑了。故第一條路徑選直徑是最優策略。

代碼

方便起見可以在求第二條路徑時將邊權取相反數，這樣就還是求最長路徑。

/*
*/
#include<bits/stdc++.h>
#define eps 0.000001
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
typedef pair<ll,int> pii;
const int N = 4e5 + 5,M = 3.2e4 + 5;
int head[N],to[N],nxt[N],val[N],dep[N],mxd[N][2],fae[N],f[N];
int mxpos,cnt;
void add(int u,int v){
	cnt++;
	to[cnt] = v;
	nxt[cnt] = head[u];
	val[cnt] = 1;
	head[u] = cnt;
}
void dfs(int x,int fa,int k){
	f[x] = fa;
	fae[x] = k;
	dep[x] = dep[fa] + val[k];
	mxd[x][0] = x;
	mxd[x][1] = x;
	for(int i=head[x];i;i = nxt[i])if(to[i] != fa){
		int nx = to[i];
		dfs(nx,x,i);
		int dnx = dep[mxd[nx][0]];
		if(dnx > dep[mxd[x][0]]){
			mxd[x][1] = mxd[x][0];
			mxd[x][0] = mxd[nx][0];
		}else if(dnx > dep[mxd[x][1]]){
			mxd[x][1] = mxd[nx][0];
		}
	}
	if(dep[mxd[x][0]] + dep[mxd[x][1]] - 2 * dep[x] > 
	   dep[mxd[mxpos][0]] + dep[mxd[mxpos][1]] - 2 * dep[mxpos] || !mxpos){
		mxpos = x;
	}
}
int main(){
//	freopen("in.txt","r",stdin);
//	freopen("out1.txt","w",stdout);
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	int n,k;
	cin>>n>>k;
	for(int i=1;i<n;i++){
		int u,v;
		cin>>u>>v;
		add(u,v);
		add(v,u);
	}
	int res = (n - 1) * 2 + k;
	dfs(1,0,0);
	res -= dep[mxd[mxpos][0]] + dep[mxd[mxpos][1]] - 2 * dep[mxpos];
	if(k == 1){
		cout<<res;
		return 0;
	}
	int now = mxd[mxpos][0];
	for(int i=1;i<=cnt;i++){
		val[i] = 1;
	}
	while(now != mxpos && now){
		val[fae[now]] = val[((fae[now] - 1) ^ 1) + 1] = -1;
		now = f[now];
	}
	now = mxd[mxpos][1];
	while(now != mxpos && now){
		val[fae[now]] = val[((fae[now] - 1) ^ 1) + 1] = -1;
		now = f[now];
	}
	mxpos = 0;
	
	dfs(1,0,0);
	res -= dep[mxd[mxpos][0]] + dep[mxd[mxpos][1]] - 2 * dep[mxpos];
	cout<<res;
	return 0;
}
/*
*/