Loading

「學習筆記」AC 自動機

AC。。。自動機？

AC 自動機是 以 Trie 的結構為基礎，結合 KMP 的思想 建立的自動機，用于解決多模式匹配等任務。

Trie 的構建

這里需要仔細解釋一下 Trie 的結點的含義，Trie 中的結點表示的是某個模式串的前綴。我們在后文也將其稱作狀態。一個結點表示一個狀態，Trie 的邊就是狀態的轉移。

形式化地說，對于若干個模式串 \(s_1, s_2 \dots s_n\)，將它們構建一棵字典樹后的所有狀態的集合記作 Q。

失配指針

個人感覺這里是最難理解的。

AC 自動機利用一個 fail 指針來輔助多模式串的匹配。

狀態 \(u\) 的 fail 指針指向另一個狀態 \(v\)，其中 \(v \in Q\)，且 \(v\) 是 \(u\) 的最長后綴（即在若干個后綴狀態中取最長的一個作為 fail 指針）。

只需要知道，AC 自動機的失配指針指向當前狀態的最長后綴狀態即可。

構建指針

構建 fail 指針，可以參考 KMP 中構造 Next 指針的思想。

考慮字典樹中當前的結點 \(u\)，\(u\) 的父結點是 \(p\)，\(p\) 通過字符 \(c\) 的邊指向 \(u\)，即 \(trie[p,\mathtt{c}]=u\)。假設深度小于 \(u\) 的所有結點的 fail 指針都已求得。

如果 \(\text{trie}[\text{fail}[p],\mathtt{c}]\) 存在：則讓 \(u\) 的 fail 指針指向 \(\text{trie}[\text{fail}[p],\mathtt{c}]\)。相當于在 \(p\) 和 \(\text{fail}[p]\) 后面加一個字符 \(c\)，分別對應 \(u\) 和 fail[u]。
如果 \(\text{trie}[\text{fail}[p],\mathtt{c}]\) 不存在：那么我們繼續找到 \(\text{trie}[\text{fail}[\text{fail}[p]],\mathtt{c}]\)。重復 \(1\) 的判斷過程，一直跳 fail 指針直到根結點。
如果真的沒有，就讓 fail 指針指向根結點。
如此即完成了 \(\text{fail}[u]\) 的構建。

如此即完成了 \(\text{fail}[u]\) 的構建。

實現

定義

struct node {
    int fail;
    int tr[26];
    int End;
} ac[N];

fail 是失配指針，tr 是字典樹，End 是當前狀態是否為一個字符串的結束。

插入

這里就是最基本的字典樹插入操作。

void Insert(char* s) {
    int l = strlen(s), u = 0;
    for (int i = 0; i < l; ++ i) {
        if (ac[u].tr[s[i] - 'a'] == 0) {
            ac[u].tr[s[i] - 'a'] = ++ tot;
        }
        u = ac[u].tr[s[i] - 'a'];
    }
    ++ ac[u].End;
}

構建失敗指針

我們用隊列廣搜的方式來構建失敗指針，按照上面的步驟：

如果 \(\text{trie}[\text{fail}[p],\mathtt{c}]\) 存在：則讓 \(u\) 的 fail 指針指向 \(\text{trie}[\text{fail}[p],\mathtt{c}]\)。相當于在 \(p\) 和 \(\text{fail}[p]\) 后面加一個字符 \(c\)，分別對應 \(u\) 和 fail[u]。
如果 \(\text{trie}[\text{fail}[p],\mathtt{c}]\) 不存在：那么我們繼續找到 \(\text{trie}[\text{fail}[\text{fail}[p]],\mathtt{c}]\)。重復 \(1\) 的判斷過程，一直跳 fail 指針直到根結點。
如果真的沒有，就讓 fail 指針指向根結點。
如此即完成了 \(\text{fail}[u]\) 的構建。

void get_fail() {
	queue<int> q;
	for (int i = 0; i < 26; ++ i) {
		if (ac[0].tr[i] != 0) {
			ac[ac[0].tr[i]].fail = 0;
			q.emplace(ac[0].tr[i]);
		}
	}
	while (!q.empty()) {
		int u = q.front();
		q.pop();
		for (int i = 0; i < 26; ++ i) {
			if (ac[u].tr[i]) {
				ac[ac[u].tr[i]].fail = ac[ac[u].fail].tr[i];
				q.emplace(ac[u].tr[i]);
			} else {
				ac[u].tr[i] = ac[ac[u].fail].tr[i];
			}
		}
	}
}

查詢

這里我們用模板題來說明。

查詢有多少個模式串出現過

P3808 【模板】AC 自動機（簡單版） - 洛谷 | 計算機科學教育新生態 (luogu.com.cn)

int ask(char* s) {
	int l = strlen(s);
	int u = 0, ans = 0;
	for (int i = 0; i < l; ++ i) {
		u = ac[u].tr[s[i] - 'a'];
		for (int cur = u; cur && (~ac[cur].End); cur = ac[cur].fail) {
			ans += ac[cur].End;
			ac[cur].End = -1;
		}
	}
	return ans;
}

這里給 End 打上標記，是為了防止重復搜到這一個模式串，然后重復加入了答案。

完整代碼：

/*
  The code was written by yifan, and yifan is neutral!!!
 */

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

template<typename T>
inline T read() {
	T x = 0;
	bool fg = 0;
	char ch = getchar();
	while (ch < '0' || ch > '9') {
		fg |= (ch == '-');
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = (x << 3) + (x << 1) + (ch ^ 48);
		ch = getchar();
	}
	return fg ? ~x + 1 : x;
}

const int N = 1e6 + 5;

int n, tot;
char s[N];

struct node {
	int fail;
	int tr[26];
	int End;
} ac[N];

void Insert(char* s) {
	int l = strlen(s), u = 0;
	for (int i = 0; i < l; ++ i) {
		if (ac[u].tr[s[i] - 'a'] == 0) {
			ac[u].tr[s[i] - 'a'] = ++ tot;
		}
		u = ac[u].tr[s[i] - 'a'];
	}
	++ ac[u].End;
}

void get_fail() {
	queue<int> q;
	for (int i = 0; i < 26; ++ i) {
		if (ac[0].tr[i] != 0) {
			ac[ac[0].tr[i]].fail = 0;
			q.emplace(ac[0].tr[i]);
		}
	}
	while (!q.empty()) {
		int u = q.front();
		q.pop();
		for (int i = 0; i < 26; ++ i) {
			if (ac[u].tr[i]) {
				ac[ac[u].tr[i]].fail = ac[ac[u].fail].tr[i];
				q.emplace(ac[u].tr[i]);
			} else {
				ac[u].tr[i] = ac[ac[u].fail].tr[i];
			}
		}
	}
}

int ask(char* s) {
	int l = strlen(s);
	int u = 0, ans = 0;
	for (int i = 0; i < l; ++ i) {
		u = ac[u].tr[s[i] - 'a'];
		for (int cur = u; cur && (~ac[cur].End); cur = ac[cur].fail) {
			ans += ac[cur].End;
			ac[cur].End = -1;
		}
	}
	return ans;
}

int main() {
	n = read<int>();
	for (int i = 1; i <= n; ++ i) {
		scanf("%s", s + 1);
		Insert(s + 1);
	}
	ac[0].fail = 0;
	get_fail();
	scanf("%s", s + 1);
	cout << ask(s + 1) << '\n';
	return 0;
}

查詢出現次數最多的模式串

P3796 【模板】AC 自動機（加強版） - 洛谷 | 計算機科學教育新生態 (luogu.com.cn)

這里 End 存儲的不再是簡單的 \(1\) 了，而是當前這個狀態對應的模式串的編號，目的是最后輸出字符串。

void Insert(string s, int num) {
	int u = 0, l = s.size();
	for (int i = 0; i < l; ++ i) {
		if (!ac[u].tr[s[i] - 'a']) {
			ac[u].tr[s[i] - 'a'] = ++ cnt;
			clr(cnt);
		}
		u = ac[u].tr[s[i] - 'a'];
	}
	ac[u].End = num;
}

for (int i = 1; i <= n; ++ i) {
	cin >> st[i];
	Insert(st[i], i);
	Ans[i].first = 0;
	Ans[i].second = i;
}

除了查詢和主函數，其他代碼都是一樣的。

查詢代碼：

void ask(char* s) {
	int l = strlen(s);
	int u = 0;
	for (int i = 0; i < l; ++ i) {
		u = ac[u].tr[s[i] - 'a'];
		for (int cur = u; cur; cur = ac[cur].fail) {
			++ Ans[ac[cur].End].first;
		}
	}
}

這里的 Ans 是定義的答案數組，first 是記錄出現的次數，second 是該狀態的編號。

完整代碼：

/*
  The code was written by yifan, and yifan is neutral!!!
 */

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;

template<typename T>
inline T read() {
	T x = 0;
	bool fg = 0;
	char ch = getchar();
	while (ch < '0' || ch > '9') {
		fg |= (ch == '-');
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = (x << 3) + (x << 1) + (ch ^ 48);
		ch = getchar();
	}
	return fg ? ~x + 1 : x;
}

const int N = 1e6 + 5;

int n, cnt;
char s[N];
string st[200];

struct node {
	int fail, End;
	int tr[26];
} ac[N];

pair<int, int> Ans[N];

void clr(int u) {
	for (int i = 0; i < 26; ++ i) {
		ac[u].tr[i] = 0;
	}
	ac[u].fail = ac[u].End = 0;
}

void Insert(string s, int num) {
	int u = 0, l = s.size();
	for (int i = 0; i < l; ++ i) {
		if (!ac[u].tr[s[i] - 'a']) {
			ac[u].tr[s[i] - 'a'] = ++ cnt;
			clr(cnt);
		}
		u = ac[u].tr[s[i] - 'a'];
	}
	ac[u].End = num;
}

void get_fail() {
	queue<int> q;
	for (int i = 0; i < 26; ++ i) {
		if (ac[0].tr[i] != 0) {
			ac[ac[0].tr[i]].fail = 0;
			q.emplace(ac[0].tr[i]);
		}
	}
	while (!q.empty()) {
		int u = q.front();
		q.pop();
		for (int i = 0; i < 26; ++ i) {
			if (ac[u].tr[i]) {
				ac[ac[u].tr[i]].fail = ac[ac[u].fail].tr[i];
				q.emplace(ac[u].tr[i]);
			} else {
				ac[u].tr[i] = ac[ac[u].fail].tr[i];
			}
		}
	}
}

void ask(char* s) {
	int l = strlen(s);
	int u = 0;
	for (int i = 0; i < l; ++ i) {
		u = ac[u].tr[s[i] - 'a'];
		for (int cur = u; cur; cur = ac[cur].fail) {
			++ Ans[ac[cur].End].first;
		}
	}
}

void work() {
	cnt = 0;
	clr(0);
	for (int i = 1; i <= n; ++ i) {
		cin >> st[i];
		Insert(st[i], i);
		Ans[i].first = 0;
		Ans[i].second = i;
	}
	get_fail();
	scanf("%s", s + 1);
	ask(s + 1);
	sort(Ans + 1, Ans + n + 1, [](pii x, pii y) {
		return x.first == y.first ? x.second < y.second : x.first > y.first;
	});
	int l = 1;
	printf("%d\n", Ans[1].first);
	while (Ans[l].first == Ans[1].first) {
		cout << st[Ans[l].second] << '\n';
		++ l;
	}
}

int main() {
	n = read<int>();
	while (n) {
		work();
		n = read<int>();
	}
	return 0;
}

優化

先拿這道題來引入。P5357 【模板】AC 自動機（二次加強版） - 洛谷 | 計算機科學教育新生態 (luogu.com.cn)

你會發現它與 P3796 【模板】AC 自動機（加強版） - 洛谷 | 計算機科學教育新生態 (luogu.com.cn) 十分的相似，似乎只要將最后的找出現次數最大的模式串改為輸出所有模式串的出現次數就行了 ~~反正當時我是這樣想的~~，然后略微修改代碼后交上發現。

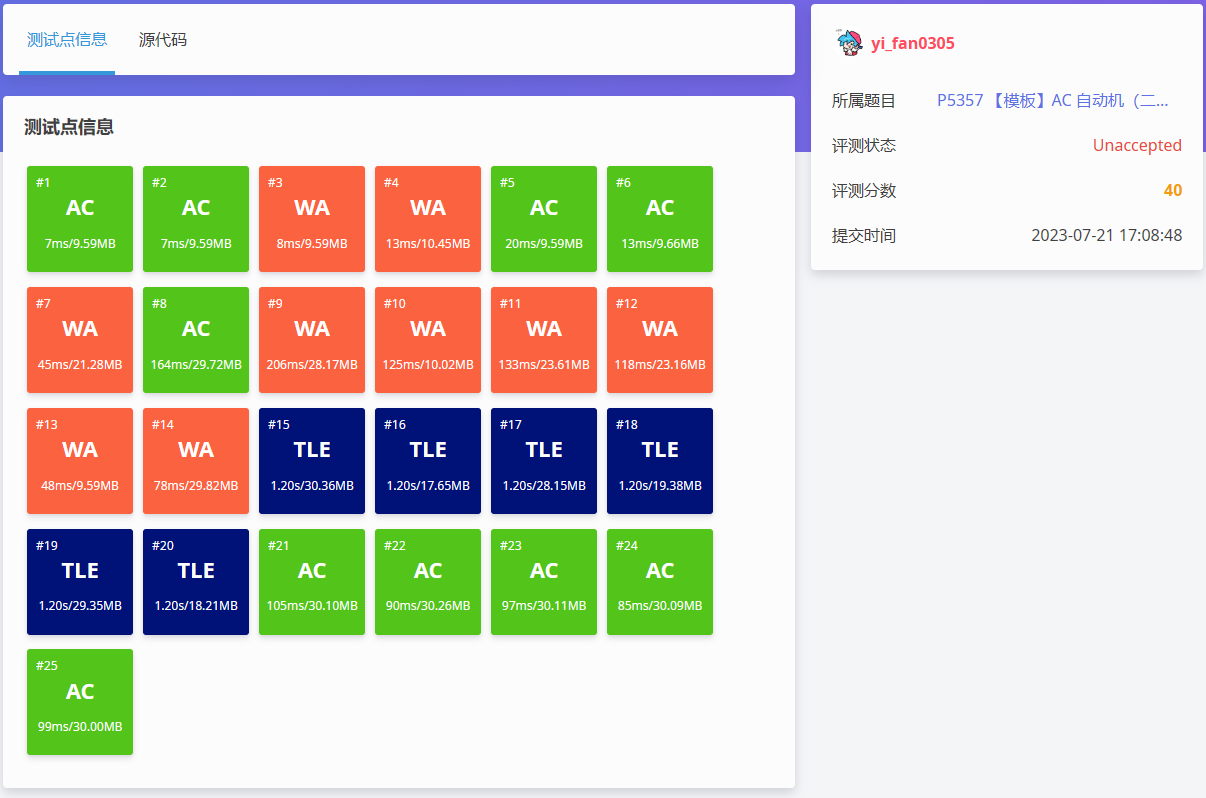
果然，二次加強版就是不一樣……

重新讀題，意外發現最后一句話：數據不保證任意兩個模式串不相同。

？？？不保證，讀錯題了！（不要犯這樣的低級錯誤），這里還是比較簡單的，只需要判一下重就好了，直接上代碼，相信看到這里的聰明的你一定可以看懂它！修改的主要位置加上注釋了。

/*
  The code was written by yifan, and yifan is neutral!!!
 */

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

template<typename T>
inline T read() {
	T x = 0;
	bool fg = 0;
	char ch = getchar();
	while (ch < '0' || ch > '9') {
		fg |= (ch == '-');
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = (x << 3) + (x << 1) + (ch ^ 48);
		ch = getchar();
	}
	return fg ? ~x + 1 : x;
}

const int N = 2e5 + 5;
const int M = 2e6 + 5;

int n, tot;
int ans[N], mp[N];
string st[N];
char s[M];
queue<int> q;

struct node {
	int End, fail;
	int tr[26];
} ac[N];

void Insert(string s, int num) {
	int l = s.length(), u = 0;
	for (int i = 0; i < l; ++ i) {
		if (!ac[u].tr[s[i] - 'a']) {
			ac[u].tr[s[i] - 'a'] = ++ tot;
		}
		u = ac[u].tr[s[i] - 'a'];
	}
	if (!ac[u].End) {// 修改點 1
		ac[u].End = num;
	}
	mp[num] = ac[u].End;
}

void get_fail() {
	for (int i = 0; i < 26; ++ i) {
		if (ac[0].tr[i]) {
			ac[ac[0].tr[i]].fail = 0;
			q.emplace(ac[0].tr[i]);
		}
	}
	while (!q.empty()) {
		int u = q.front();
		q.pop();
		for (int i = 0; i < 26; ++ i) {
			if (ac[u].tr[i]) {
				ac[ac[u].tr[i]].fail = ac[ac[u].fail].tr[i];
				q.emplace(ac[u].tr[i]);
			} else {
				ac[u].tr[i] = ac[ac[u].fail].tr[i];
			}
		}
	}
}

void ask(char* s) {
	int l = strlen(s), u = 0;
	for (int i = 0; i < l; ++ i) {
		u = ac[u].tr[s[i] - 'a'];
		for (int cur = u; cur; cur = ac[cur].fail) {
			++ ans[ac[cur].End];
		}
	}
}

int main() {
	n = read<int>();
	for (int i = 1; i <= n; ++ i) {
		cin >> st[i];
		Insert(st[i], i);
	}
	get_fail();
	scanf("%s", s + 1);
	ask(s + 1);
	for (int i = 1; i <= n; ++ i) {
		printf("%d\n", ans[mp[i]]); // 修改點 2
	}
	return 0;
}

再次提交，得到了這樣的結果。

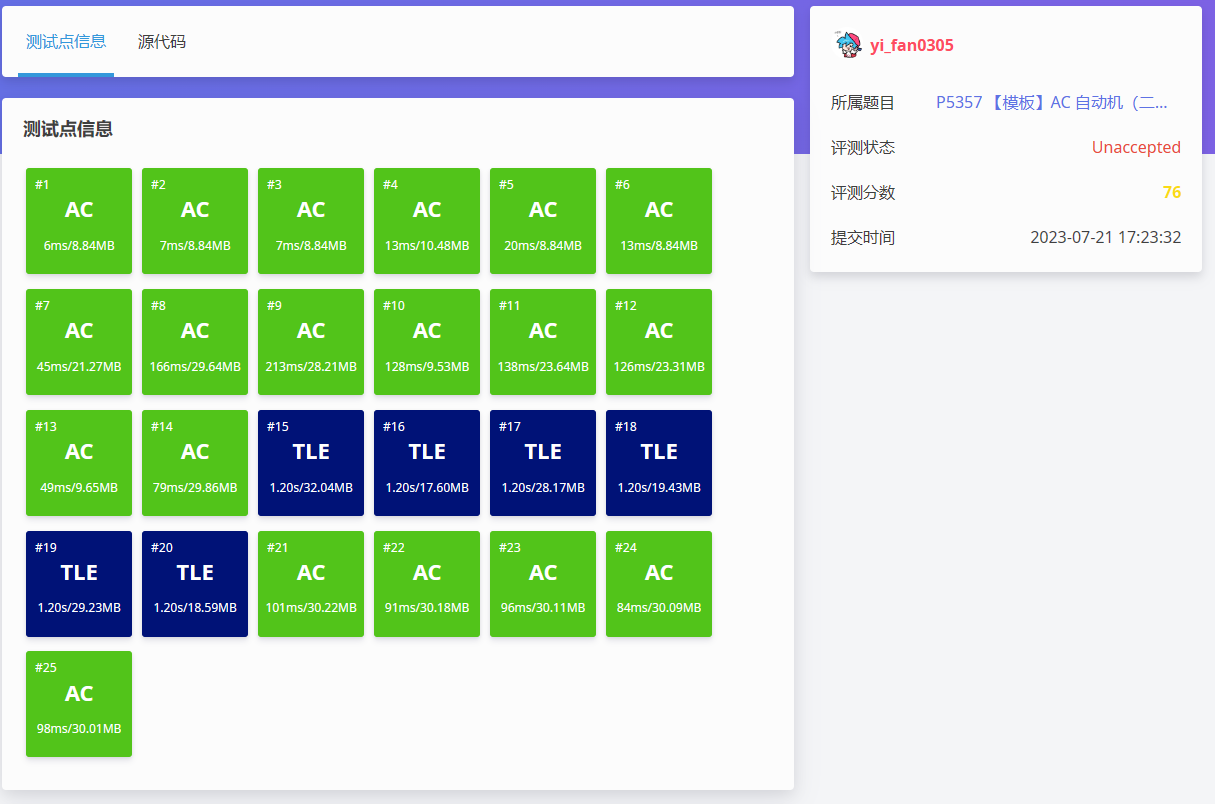
沒辦法，去 \(\texttt{OI-Wiki}\) 上看了看，發現原來有優化，優化的方式使用 拓撲排序！

不會拓撲排序的朋友先去學習一下拓撲排序吧。拓撲排序 - OI Wiki (oi-wiki.org)

我們為什么會 T 呢？

看這段代碼

void ask(char* s) {
	int l = strlen(s), u = 0;
	for (int i = 0; i < l; ++ i) {
		u = ac[u].tr[s[i] - 'a'];
		for (int cur = u; cur; cur = ac[cur].fail) {
			++ ans[ac[cur].End];
		}
	}
}

我們沿著 fail 指針一步一步地跳，對于下面的圖。

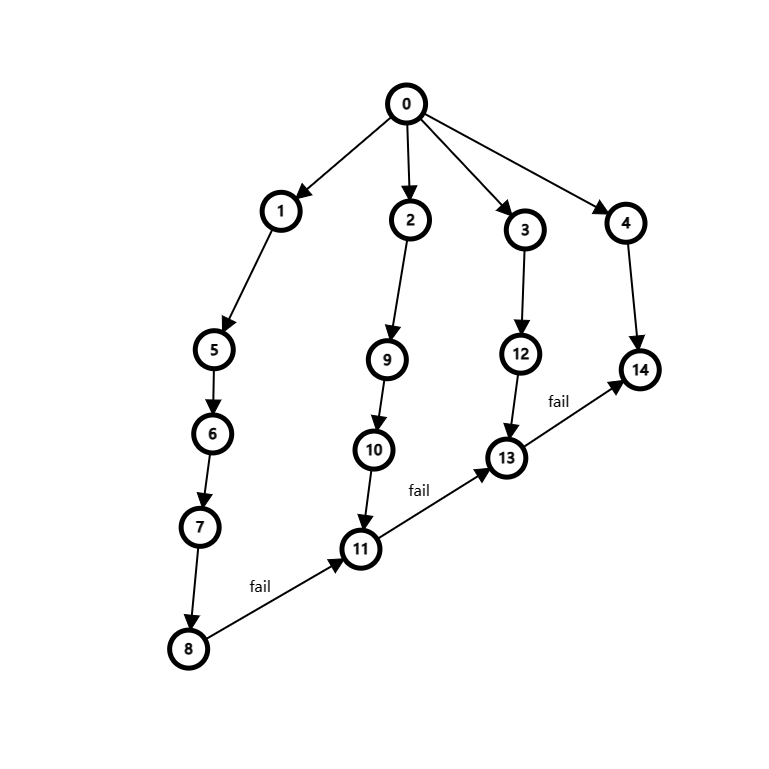
我們假設：

先搜到 \(14\) 號節點，答案更新；然后搜到了 \(13\) 號節點，答案更新，再找到 \(14\) 號節點，答案更新；之后搜到了 \(11\) 號節點，順著 fail 答案更新；再之后搜到了 \(8\) 號節點，順著 fail 答案更新。

你會發現，效率慢的很！然后就被這道題卡了。

如何提高效率的，我們可以在 \(8、11、13、14\) 號節點上各打上標記，然后從 \(8\) 號開始，標記順著 fail 傳遞過去，最后統計的答案為：\(8\) 號統計了 \(1\) 次，\(11\) 號統計了 \(2\) 次，\(13\) 號統計了 \(3\) 次，\(14\) 號統計了 \(4\) 次，這樣統計的答案與一次又一次地更新是一樣的，但是這種方法效率高了很多。

具體怎么實現呢，就用拓撲排序，把 fail 指針作為邊，最后 fail 指針一定不會成環，所以可以跑拓撲排序，修改一下代碼就可以了。

/*
  The code was written by yifan, and yifan is neutral!!!
 */

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

template<typename T>
inline T read() {
	T x = 0;
	bool fg = 0;
	char ch = getchar();
	while (ch < '0' || ch > '9') {
		fg |= (ch == '-');
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = (x << 3) + (x << 1) + (ch ^ 48);
		ch = getchar();
	}
	return fg ? ~x + 1 : x;
}

const int N = 2e5 + 5;
const int M = 2e6 + 5;

int n, tot;
int ans[N], mp[N], in[N];
string st[N];
char s[M];
queue<int> q;

struct node {
	int End, fail, tag;
	int tr[26];
} ac[N];

void Insert(string s, int num) {
	int l = s.length(), u = 0;
	for (int i = 0; i < l; ++ i) {
		if (!ac[u].tr[s[i] - 'a']) {
			ac[u].tr[s[i] - 'a'] = ++ tot;
		}
		u = ac[u].tr[s[i] - 'a'];
	}
	if (!ac[u].End) {
		ac[u].End = num;
	}
	mp[num] = ac[u].End;
}

void get_fail() {
	for (int i = 0; i < 26; ++ i) {
		if (ac[0].tr[i]) {
			ac[ac[0].tr[i]].fail = 0;
			q.emplace(ac[0].tr[i]);
		}
	}
	while (!q.empty()) {
		int u = q.front();
		q.pop();
		for (int i = 0; i < 26; ++ i) {
			if (ac[u].tr[i]) {
				ac[ac[u].tr[i]].fail = ac[ac[u].fail].tr[i];
				q.emplace(ac[u].tr[i]);
				++ in[ac[ac[u].fail].tr[i]];
			} else {
				ac[u].tr[i] = ac[ac[u].fail].tr[i];
			}
		}
	}
}

void ask(char* s) {
	int l = strlen(s), u = 0;
	for (int i = 0; i < l; ++ i) {
		u = ac[u].tr[s[i] - 'a'];
		++ ac[u].tag; // 修改部分 1
	}
}

void topsort() { // 修改部分 2
	for (int i = 1; i <= tot; ++ i) {
		if (!in[i]) {
			q.emplace(i);
		}
	}
	while (!q.empty()) {
		int fr = q.front();
		q.pop();
		ans[ac[fr].End] = ac[fr].tag;
		int u = ac[fr].fail;
		ac[u].tag += ac[fr].tag;
		if (! (-- in[u])) {
			q.emplace(u);
		}
	}
}

int main() {
	n = read<int>();
	for (int i = 1; i <= n; ++ i) {
		cin >> st[i];
		Insert(st[i], i);
	}
	get_fail();
	scanf("%s", s + 1);
	ask(s + 1);
	topsort();
	for (int i = 1; i <= n; ++ i) {
		printf("%d\n", ans[mp[i]]);
	}
	return 0;
}

然后，我們就得到了想要的 AC！

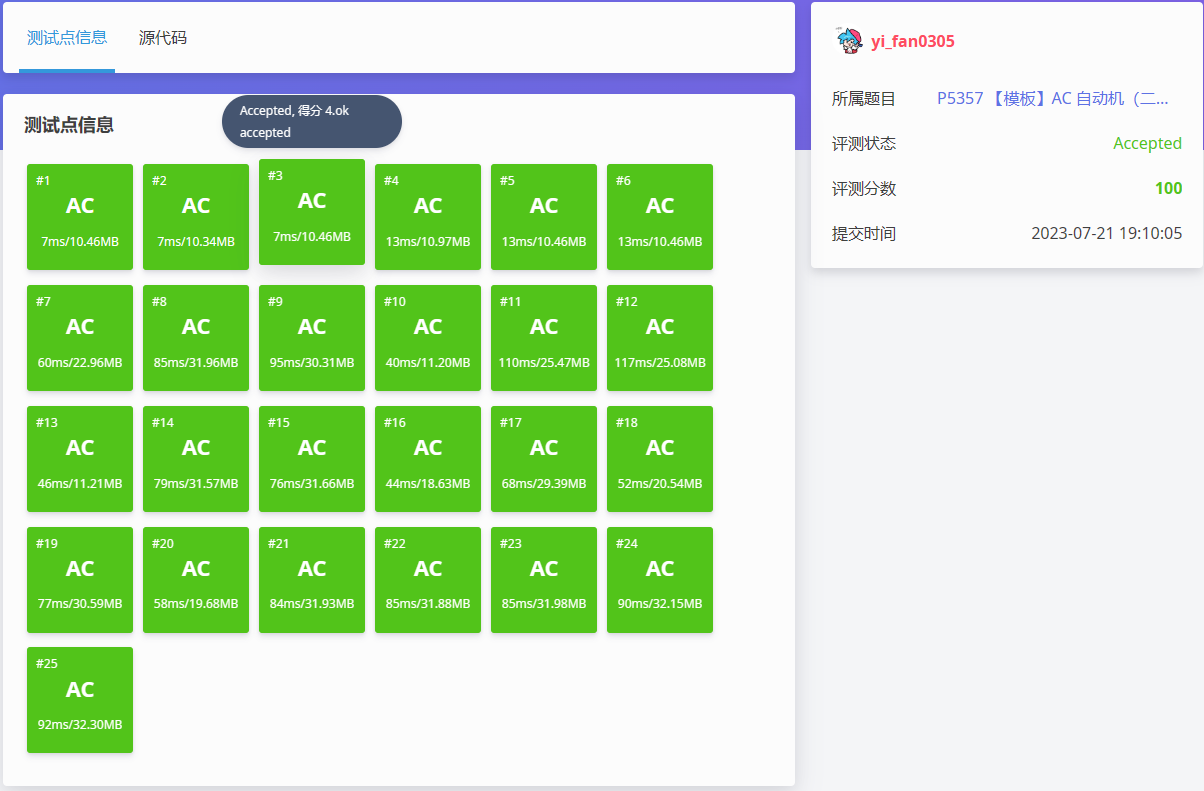
完結！

posted @ 2023-07-21 21:03 yi_fan0305 閱讀(233) 評論(1) 收藏舉報

刷新頁面返回頂部

Loading

朝氣蓬勃后生可畏

四葉草少年，你將何去何從？

「學習筆記」AC 自動機

Trie 的構建

失配指針

構建指針

實現

定義

插入

構建失敗指針

查詢

查詢有多少個模式串出現過

查詢出現次數最多的模式串

優化

公告

Loading

朝氣蓬勃 后生可畏

四葉草少年，你將何去何從？

「學習筆記」AC 自動機

Trie 的構建

失配指針

構建指針

實現

定義

插入

構建失敗指針

查詢

查詢有多少個模式串出現過

查詢出現次數最多的模式串

優化

公告

朝氣蓬勃后生可畏