「學習筆記」后綴數組
感謝 LB 學長的博文!
2023.7.13 做了一點知識的補充(height 數組)。
2023.8.24 做了一點關于應用的補充。
前置知識
后綴是指從某個位置 \(i\) 開始到整個串末尾結束的一個特殊子串,也就是 \(S[i : |S|-1]\)。字符串 \(S\) 的從 \(i\) 開頭的后綴表示為 \(\textit{Suffix(S,i)}\),也就是 \(\textit{Suffix(S,i)}=S[i : |S|-1]\)。
變量
后綴數組最主要的兩個數組是 sa 和 rk。
sa 表示將所有后綴排序后第 \(i\) 小的后綴的編號,即編號數組。
rk 表示后綴 \(i\) 的排名,即排名數組。
這兩個數組滿足一個重要性質: sa[rk[i]] = rk[sa[i]] = i。
示例:
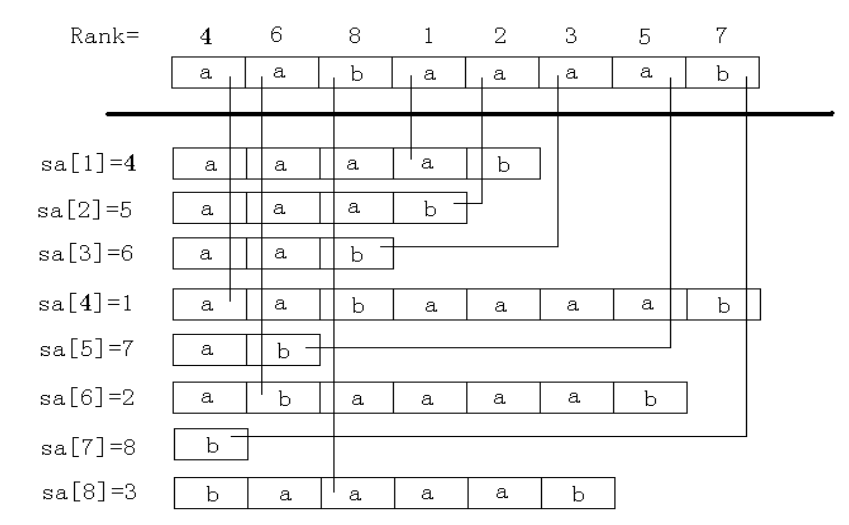
這個圖很好理解。
做法
暴力的 \(O_{n^2 \log n}\) 做法
將所有的后綴數組都 sort 一遍,sort 復雜度為 \(O_{n \log n}\),字符串比較復雜度為 \(O_{n}\),總的復雜度 \(O_{n^2 \log n}\)。
/*
The code was written by yifan, and yifan is neutral!!!
*/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
template<typename T>
inline T read() {
T x = 0;
bool fg = 0;
char ch = getchar();
while (ch < '0' || ch > '9') {
fg |= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return fg ? ~x + 1 : x;
}
const int N = 1e6 + 5;
int n;
char s[N];
string h[N];
pair<string, int> ans[N];
int main() {
scanf("%s", s + 1);
n = strlen(s + 1);
for (int i = 1; i <= n; ++ i) {
for (int j = i; j <= n; ++ j) {
h[i] += s[j];
}
ans[i] = {h[i], i};
}
sort(ans + 1, ans + n + 1);
for (int i = 1; i <= n; ++ i) {
cout << ans[i].second << ' ';
}
return 0;
}
倍增優化的 \(O_{n \log^2 n}\) 做法
先對長度為 \(1\) 的所有子串,即每個字符排序,得到排序后的 sa1 和 rk1 數組。
之后倍增:
-
用兩個長度為 \(1\) 的子串的排名,即
rk1[i]和rk1[i + 1],作為排序的第一關鍵詞和第二關鍵詞,這樣就可以對每個長度為 \(2\) 的子串進行排序,得到sa2和rk2; -
之后用兩個長度為 \(2\) 的子串的排名,即
rk2[i]和rk2[i + 2],來作為排序的第一關鍵詞和第二關鍵詞。(為什么是 \(i + 2\) 呢,因為rk2[i]和rk2[i + 1]重復了 \(S_{i + 1}\))這樣就可以對每個長度為 \(4\) 的子串進行排序,得到sa4和rk4; -
重復上面的操作,用兩個長度為 \(\dfrac{w}{2}\) 的子串的排名,即
rk[i]和rk[i + (w / 2)],來作為排序的第一關鍵詞和第二關鍵詞,直到 \(w \ge n\),最終得到的sa數組就是我們的答案數組。
示意圖:

倍增的復雜度為 \(O_{\log n}\),sort 復雜度為 \(O_{n \log n}\),總的復雜度 \(O_{n \log ^ 2 n}\)。
排序優化的 \(O_{n \log n}\) 的做法
發現后綴數組值域即為 \(n\),又是多關鍵字排序,考慮基數排序。
上面已經給出一個用于比較的式子:(A[i] < A[j] or (A[i] = A[j] and B[i] < B[j])),倍增過程中 A[i], B[i] 大小關系已知,先將 B[i] 作為第二關鍵字排序,再將 A[i] 作為第一關鍵字排序,兩次計數排序實現即可。
單次計數排序復雜度 \(O_{n+w}\)(\(w\) 為值域,顯然最大與 \(n\) 同階),總時間復雜度變為 \(O_{n \log n}\)。
//The code was written by yifan, and yifan is neutral!!!
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define bug puts("NOIP rp ++!");
#define rep(i, a, b, c) for (int i = (a); i <= (b); i += (c))
#define per(i, a, b, c) for (int i = (a); i >= (b); i -= (c))
template<typename T>
inline T read() {
T x = 0;
bool fg = 0;
char ch = getchar();
while (ch < '0' || ch > '9') {
fg |= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return fg ? ~x + 1 : x;
}
const int N = 1e6 + 5;
int n, m;
int sa[N], tmpsa[N], rk[N << 1], tmprk[N << 1], cnt[N];
// rk 第 i 個后綴的排名,sa 第 i 小的后綴的編號
char s[N];
int main() {
scanf("%s", s + 1);
n = strlen(s + 1);
m = 127;
/*--------------------------------*/
// 計數排序
rep (i, 1, n, 1) {
++ cnt[rk[i] = s[i]];
}
rep (i, 1, m, 1) {
cnt[i] += cnt[i - 1];
}
per (i, n, 1, 1) {
sa[cnt[rk[i]] --] = i;
}
memcpy(tmprk + 1, rk + 1, n * sizeof(int));
/*--------------------------------*/
// 判重
for (int cur = 0, i = 1; i <= n; ++ i) {
if (tmprk[sa[i]] == tmprk[sa[i - 1]]) {
rk[sa[i]] = cur;
}
else {
rk[sa[i]] = ++ cur;
}
}
/*--------------------------------*/
for (int w = 1; w < n; w <<= 1, m = n) {
// 先按照第二關鍵詞計數排序
memset(cnt, 0, sizeof cnt);
memcpy(tmpsa + 1, sa + 1, n * sizeof(int));
for (int i = 1; i <= n; ++ i) {
++ cnt[rk[tmpsa[i] + w]]; // rk[oldsa[i] + w] (第i小的編號 + w) 位置的排名
}
for (int i = 1; i <= m; ++ i) {
cnt[i] += cnt[i - 1];
}
for (int i = n; i >= 1; -- i) {
sa[cnt[rk[tmpsa[i] + w]] --] = tmpsa[i];
}
/*--------------------------------*/
// 再按照第一關鍵詞計數排序
memset(cnt, 0, sizeof cnt);
memcpy(tmpsa + 1, sa + 1, n * sizeof(int));
for (int i = 1; i <= n; ++ i) {
++ cnt[rk[tmpsa[i]]];
}
for (int i = 1; i <= m; ++ i) {
cnt[i] += cnt[i - 1];
}
for (int i = n; i >= 1; -- i) {
sa[cnt[rk[tmpsa[i]]] --] = tmpsa[i];
}
/*--------------------------------*/
// 更新數組
memcpy(tmprk + 1, rk + 1, n * sizeof(int));
for (int cur = 0, i = 1; i <= n; ++ i) {
if (tmprk[sa[i]] == tmprk[sa[i - 1]] && tmprk[sa[i] + w] == tmprk[sa[i - 1] + w]) {
rk[sa[i]] = cur;
}
else {
rk[sa[i]] = ++ cur;
}
}
}
for (int i = 1; i <= n; ++ i) {
printf("%d ", sa[i]);
}
return 0;
}
給在第二關鍵詞排序時,sa[i] 存儲的是第二關鍵詞第 \(i\) 小的后綴的編號,但是并沒有修改 rk。之后再給第一關鍵詞排序時,oldsa 存儲的是 sa 的信息,rk 依舊沒有變,只要 rk 沒有變,計數排序就不會被影響。從后往前更新,是為了在第一關鍵詞相等時,可以直接利用第二關鍵詞的排序。
為什么先按第二關鍵詞排序,而不是先按第一關鍵詞排序呢?
從代碼里我們可以看到,先按照第二關鍵詞排序,然后再給第一關鍵詞排序時,是在第二關鍵詞的基礎上進行的,這樣的用處是當第一關鍵詞相同時,我們不用在處理第二關鍵詞了,直接按照排序的順序依次往下放。
假設先按第一關鍵詞排序,某兩個位置的第一關鍵詞相同,那么接下來看第二關鍵詞。
在按照第二關鍵詞排序時,第一關鍵詞變成了實際意義上的第二關鍵詞了,即先按照第二關鍵詞排序,第二關鍵詞相同時,再按照第一關鍵詞排序,與我們的目的不符。
各種常數優化
- 考慮我們按照第二關鍵詞排序的實質,就是將超出 \(n\) 范圍的空字符串放在
sa的最前面,在本次排序中,\(S[sa_i : sa_i+2^k?1]\) 是長度為 \(2^k\) 的子串 \(S[sai?2^k?1 : sai+2^k?1]\) 的后半截,sa[i]的排名將作為排序的關鍵字。
\(S[sa_i : sa_i+2^k?1]\) 的排名為 \(i\),則第一次計排后 \(S[sa_i?2^k?1 : sa_i+2^k?1]\) 的排名必為 \(i\),考慮直接賦值。
我們設 tmpsa 為處理完第二關鍵詞排序的 sa 數組,即 tmpsa[i] 的含義是第二關鍵詞排名為 \(i\) 的后綴,此時的 sa 還是上一輪倍增遺留的產物,可以直接被我們利用。
for (p = 0, i = n; i > n - w; -- i) {
tmpsa[++ p] = i;
}
for (int i = 1; i <= n; ++ i) {
if (sa[i] > w) { // 保證 sa[i] 是后半截的編號
tmpsa[++ p] = sa[i] - w; // sa[i] 一定是后半截的編號,而我們要存的是前半截的開始編號
}
}
-
減小值域,每次對
rk進行更新之后,我們都計算了一個 \(p\),這個 \(p\) 即是rk的值域,將值域改成它即可。 -
將
rk[tmpsa[i]]存下來,減少不連續內存訪問。 -
用函數
cmp來計算是否重復。 -
若排名都不相同可直接生成后綴數組。
//The code was written by yifan, and yifan is neutral!!!
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define bug puts("NOIP rp ++!");
#define rep(i, a, b, c) for (int i = (a); i <= (b); i += (c))
#define per(i, a, b, c) for (int i = (a); i >= (b); i -= (c))
template<typename T>
inline T read() {
T x = 0;
bool fg = 0;
char ch = getchar();
while (ch < '0' || ch > '9') {
fg |= (ch == '-');
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return fg ? ~x + 1 : x;
}
const int N = 1e6 + 5;
int n, m;
int sa[N], rk[N << 1], tmpsa[N], tmprk[N << 1], cnt[N], key[N];
// todo sa[i]: 目前求的后綴數組排名為 i 的后綴,rk[i]: 目前求的后綴數組,后綴 i 的排名
// todo tmpsa[i]: 求的后綴數組第二關鍵字排名為 i 的后綴,tmpsa[i]: 替換作用
// todo key[i]: 當前這一輪第二關鍵字排名為 i 的第一關鍵字的排名
char s[N];
bool cmp(int x, int y, int w) {
return (tmprk[x] == tmprk[y]) && (tmprk[x + w] == tmprk[y + w]);
}
int main() {
scanf("%s", s + 1);
n = strlen(s + 1);
m = 127;
rep (i, 1, n, 1) {
++ cnt[rk[i] = s[i]];
}
rep (i, 1, m, 1) {
cnt[i] += cnt[i - 1];
}
per (i, n, 1, 1) {
sa[cnt[rk[i]] --] = i;
}
int p;
for (int w = 1; w <= n; w <<= 1, m = p) {
// todo m = p 減小值域,m 是用于給 rk 計數排序的,rk 的值域為 p,則 m 也為 p
// todo 優化 2
p = 0;
per (i, n, n - w + 1, 1) { // todo 優化 1
tmpsa[++ p] = i;
}
rep (i, 1, n, 1) {
if (sa[i] > w) {
tmpsa[++ p] = sa[i] - w;
}
}
memset(cnt, 0, sizeof cnt);
rep (i, 1, n, 1) { // todo 優化 3
++ cnt[key[i] = rk[tmpsa[i]]];
}
rep (i, 1, m, 1) { // todo 優化 2
cnt[i] += cnt[i - 1];
}
per (i, n, 1, 1) {
sa[cnt[key[i]] --] = tmpsa[i];
}
memcpy(tmprk + 1, rk + 1, n * sizeof(int));
p = 0;
rep (i, 1, n, 1) {
rk[sa[i]] = cmp(sa[i], sa[i - 1], w) ? p : ++ p;
// todo 優化 4
}
if (p == n) { // todo 優化 5
break ;
}
}
rep (i, 1, n, 1) {
cout << sa[i] << ' ';
}
return 0;
}
LCP 問題(最長公共前綴)
參考主要來自「筆記」后綴數組 - Luckyblock - 博客園 (cnblogs.com),感謝 LB 學長!
定義:
\(\operatorname{lcp}(S, T)\):定義為字符串 \(S\) 和 \(T\) 的最長公共前綴,即最大的 \(l \le \min\{|S|, |T|\}\),滿足 \(S_i = T_i (1 \le i \le l)\),在這里 \(\operatorname{lcp}(i, j)\) 表示后綴 \(i, j\) 的最長公共前綴。
定義新數組 height 和 h。
\(\operatorname{height}_i\) 表示排名為 \(i - 1\) 和 \(i\) 的兩個后綴的最長公共前綴,即 \(\operatorname{lcp}(sa_{i - 1}, sa_i)\)。
\(h_i\) 表示后綴 \(i\) 和排名在 \(i\) 之前一位的后綴的最長公共前綴,即 \(h_i= \operatorname{height}_{rk_i} = \operatorname{lcp}(sa_{rk_{i} - 1},sa_{rk_i}) = \operatorname{lcp} (sa_{rk_{i} - 1}, i)\)。
引理:LCP Lemma
\(\forall 1 \le i < j < k \le n, \operatorname{lcp}(sa_i, sa_k) = \min\{\operatorname{lcp}(sa_i, sa_j), \operatorname{lcp}(sa_j, sa_k)\}\)
證明:
設 \(p = \min \{ \operatorname{lcp}(sa_i, sa_j), \operatorname{lcp}(sa_j, sa_k) \}\),則有
即 \(sa_i \left [1 : p \right ] = sa_j \left[ 1 : p \right] = s_k \left[ 1 : p \right ]\),由此可得 \(\operatorname{lcp}(sa_i, sa_k) \ge p\)。
再考慮反證法,設 \(\operatorname{lcp}(sa_i, sa_k) = q > p\),則 \(sa_i \left [1 : q \right ] = sa_k \left[1 : q \right]\),有 \(sa_{i} \left[ p + 1 \right ] = sa_{k} \left[ p + 1 \right ]\)。
對 \(p\) 的取值進行分類討論:
-
\(p = \operatorname{lcp} (sa_i, sa_j) < \operatorname{lcp}(sa_j, sa_k)\) 時,則有 \(sa_i \left[p + 1 \right ] \ne sa_j \left [ p + 1 \right ], sa_j \left [ p + 1 \right ] = sa_k \left[ p + 1 \right ]\)。
-
\(p = \operatorname{lcp} (sa_j, sa_k) < \operatorname{lcp} (sa_i, sa_j)\) 時,則有 \(sa_k \left[ p + 1\right ] \ne sa_i \left [ p + 1 \right ], sa_i \left [ p + 1 \right ] = sa_j \left[ p + 1\right ]。\)
-
\(p = \operatorname{lcp} (sa_i, sa_j) = \operatorname{lcp} (sa_j, sa_k)\) 時,則有 \(sa_i \left[p + 1 \right ] \ne sa_j \left[ p + 1 \right ] \ne sa_k \left [p + 1 \right ]\)。
\(sa_i \left[p + 1 \right] \ne sa_k \left[p + 1 \right]\) 恒成立,與已知矛盾,則 \(\operatorname{lcp} (sa_i, sa_k) \le p\)。
引理:LCP Theorem
有 LCP Lemma 可知,顯然成立。
根據這個式子,求任意兩個后綴的 \(\operatorname{lcp}\) 問題就變為了求 \(\operatorname{height}\) 的區間最值問題。
通過 st 表預處理。
推論:LCP Corollary
表示排名不相鄰的兩個后綴的 \(\operatorname{lcp}\) 不超過它們之間任何相鄰元素的 \(\operatorname{lcp}\)。
考慮反證法。設 \(\operatorname{lcp}(sa_i, sa_j) < \operatorname{lcp}(sa_i, sa_k)\),則由下圖:

在字典序比較的過程中,若 \(sa_i < sa_j\),則有 \(sa_i \left[ \operatorname{lcp} (sa_i, sa_j) + 1 \right ] < sa_j \left [ \operatorname{lcp} (sa_i, sa_j) + 1 \right ]\),即圖中的字符 \(x < y\)。
再考慮比較 \(sa_j\) 與 \(sa_k\) 的字典序,\(\operatorname{lcp} (sa_i,sa_k) > \operatorname{lcp}(sa_i,sa_j)\),則 \(sa_k \left[ \operatorname{lcp} (sa_j, sa_k) + 1 \right ] = x\)。
又因為 \(x < y\),可以得到 \(sa_k\) 的字典序小于 \(sa_j\),與已知矛盾,反正原結論成立。
引理
現在再看一遍定義:
height[i] 表示排名為 \(i - 1\) 和 \(i\) 的兩個后綴的最長公共前綴,即 \(\operatorname{lcp}(sa_{i - 1}, sa_i)\)。
h[i] 表示后綴 \(i\) 和排名在 \(i\) 之前一位的后綴的最長公共前綴,即 \(h_i= \operatorname{height}_{rk_i} = \operatorname{lcp}(sa_{rk_{i} - 1},sa_{rk_i}) = \operatorname{lcp} (sa_{rk_{i} - 1}, i)\)。
證明:
考慮數學歸納。首先當 \(h_{i?1} \le 1\) 時,結論顯然成立,因為 \(h_i \ge 0\)。
當 \(h_{i - 1} > 1\) 時,設 \(u = i, v = sa_{rk_{i} - 1}\),有 \(h_i = \operatorname{lcp}(u, v)\)。
同時,設 \(u' = i - 1, v' = sa_{rk_{i - 1} - 1}\),有 \(h_{i - 1} = \operatorname{lcp} (u', v')\)。
由 \(h_{i - 1} = \operatorname{lcp} (u', v') > 1\),則 \(u', v'\) 必有公共前綴。
考慮刪去 \(u', v'\) 的第一個字符,設其分別變成 \(x, y\)。顯然 \(\operatorname{lcp} (x, y) = h_{i - 1} - 1\),且仍滿足字典序 \(y < x\)。
\(u' = i - 1\),則刪去第一個字符后,\(x\) 等于后綴 \(i\)。
則對于他們在 sa 中的排名,有 \(y < x = i = u\)。
在 sa 中,\(v\) 在 \(u\) 的前一位置,即 \(v < u\) 是不變的,且 \(y \le v\),結合一下,就有 \(y \le v < u\),根據 LCP Corollary (排名不相鄰的兩個后綴的 \(\operatorname{lcp}\) 不超過它們之間任何相鄰元素的 \(\operatorname{lcp}\)),有:
得證。
求 height
根據定義 \(h_i = \operatorname{height}_{rk_i}\),只需快速求出 \(h\),便可 \(O\left(n \right)\) 地獲得 \(\operatorname{height}\)。
通過引理我們得到 \(\forall 1 \le i \le n, h_i \ge h_{i - 1} - 1\)。
\(h_i = \operatorname{lcp}(i, sa_{rk_i - 1})\) 不具有完全單調性,考慮正序枚舉 \(i\) 進行遞推。
-
當 \(rk_i = 1\) 時,\(sa_{rk_{i} - 1}\) 不存在,特判 \(h_i = 0\);
-
當 \(i = 1\) 時,暴力比較出 \(\operatorname{lcp}(i, sa_{rk_i - 1})\),比較次數 \(< n\);
-
若上述情況都不滿足,由引理可知,\(h_i = \operatorname{lcp} (i, sa_{rk_i - 1}) \ge h_{i - 1} - 1\),兩個前綴前 \(h_{i - 1} - 1\) 位相同,可從第 \(h_{i - 1}\) 位開始比較兩個后綴,計算出 \(h_i\),比較次數 \(h_i - h_{i - 1} + 2\)。
在代碼中并沒有專門開 \(h\) 數組,只是為了方便理解,代碼中 \(h_i = k\)。
for (i = 1, k = 0; i <= n; height[rk[i ++]] = k) {
if (rk[i] == 1) {
k = 0;
continue ;
}
k ? -- k : k;
while (s[i + k] == s[sa[rk[i] - 1] + k]) ++ k;
}
height 數組的應用
-
兩子串的最長公共前綴
\(\operatorname{lcp}(sa_i, sa_j) = \min \{ \operatorname{height}[i + 1 : j] \}\)
可以轉化成 RMQ 問題。
-
比較兩個子串大小關系
比較 \(A = s[a:b], B = s[c:d]\) 兩個子串的大小。
如果 \(\operatorname{lcp}(A, B) < \min \{ \left |A \right |, \left | B \right | \}\),則直接比較 \(rk_a\) 和 \(rk_b\) 的大小即可。
否則,\(A < B \Longleftrightarrow \left | A \right | < \left | B \right |\)。
-
尋找不同子串的個數
子串就是后綴的前綴,可以枚舉后綴,計算前綴總數,減去重復的前綴。
\(sa_i\) 和 \(sa_{i + 1}\) 相同的前綴總數為 \(\operatorname{height[i + 1]}\),字串的總個數為 \(\dfrac{n(n + 1)}{2}\)。
計算公式:\(\dfrac{n(n + 1)}{2} - \sum_{i = 2}^{n} \operatorname{height[i]}\)
-
出現至少 k 次的子串的最大長度
求出相鄰 \(k - 1\) 個 \(\operatorname{height}\) 的最小值,在對最小值求最大值即可。
參考資料
后綴數組簡介 - OI Wiki (oi-wiki.org)
「筆記」后綴數組 - Luckyblock - 博客園 (cnblogs.com)
后記
字符串一類的算法,本蒟蒻一直都有點繞不過來,后綴數組,從最開始的暴力、sort,到計數排序、基數排序優化,再到常數優化,再到 height 數組,前后花了近兩天的時間,但是,自己能通過各種方式把這個東西給啃下來,還是感覺很有成就感的!


 浙公網安備 33010602011771號
浙公網安備 33010602011771號