倍增

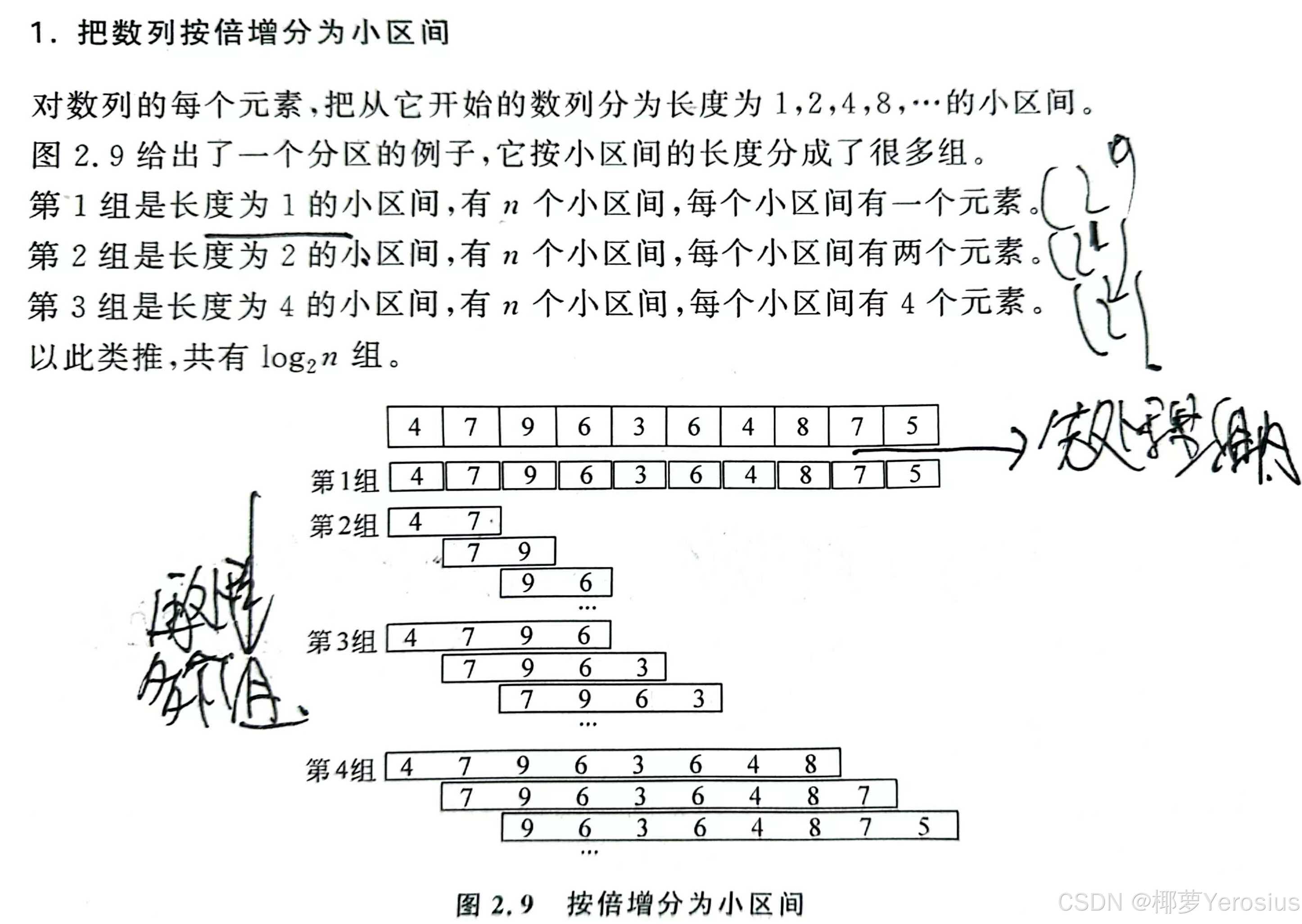
倍增是與二分相反的算法，其核心思想是每次擴大一倍，以$2^n$的速度極大擴展空間

• 原理：任意整數均可被分解為若干個以2為底的冪項和。最經典的倍增是$2^i$(實際應為$e^i$)

• 流程：定義倍增表$g[i][j]$,其中$i$代表起始元素索引，$j$代表倍增組數(該組對應區間長度(包含原元素本身)為$2^j$，該元素在該組中倍增后的位置為$i+2^j?1$)。$n$個元素最多可倍增${\log }_{2}n$組(經驗值在20左右)。

• 倍增遞推式：$g[i][j]=g[g[i][j?1]][j?1]$

• 含義:第$i$個元素倍增$j$組，等于其倍增$j?1$組后再倍增$j?1$組，即$i+2^j=(i+2^{j?1})+2^{j?1}$。特別地，當$j=0$時，表示其倍增$0$組，倍增區間長度為$2^0$，即為$i$本身

void init(){
    for(int i=0;i<n;i++) g[i][0]=i;
    for(int j=1;j<=log2(n);j++)//倍增輪數,或寫成(1<<j)<=n
        for(int i=0;i<n;i++)//逐步處理每組組內倍增
            g[i][j]=g[g[i][j-1]][j-1];
}

• 優化：打表計算所有用到的${\log }_2$

extern vector<int>l2(n+1);
void calc(){
    l2[0]=-1;
    for(int i=1;i<=n;i++) l2[i]=l2[i>>1]+1;
}

倍增法具有極其廣泛的應用，可用于求解ST表、LCA等問題。

ST表

可重復貢獻性問題：對于運算$\text{opt}$，若滿足$x\text{opt}x=x$，即重復該運算對答案無影響，則$\text{opt}$稱為可重復貢獻性運算，其對應的區間詢問就是一個可重復貢獻問題。常見的$\text{opt}=\text{max/min},\text{gcd}$等，但$\text{opt}\ne \sum ,\prod$等。

可重復貢獻性常用于兩個交集$\ne ?$的區間合并。若大區間能被$n$個小區間所覆蓋,則$\text{opt}$(大區間)=$\text{opt}$(小區間1,$?$ ,小區間$n$)。

ST表用于高效解決具有可重復貢獻性問題的數據結構，其基于倍增的思想。

ST表求解靜態區間RMQ問題

問題：給定長度為$n$的靜態序列(無任何修改操作)，有$m$次詢問，每次給定$L,R$，查詢序列區間$[L,R]$內的最值，必須以$O(1)$復雜度回答每次詢問。

初始化ST表 $O(n{\log }_{2}n)$

流程：定義$dp[s][k]$表示區間$[s,s+2^k)$內的最值，根據鴿巢原理，$[s,s+2^k)$的區間最值必定為$最值($區間$[s,s+2^{k?1})$內的最值和區間$[s+2^{k?1},s+2^k)$內的最值$)$。

狀態轉移方程式：$dp[s][k]=RMQ(dp[s][k?1],dp[s+(1?(k?1))][k?1])$

extern int dp[MAX][log2(n)+10];
int opt(int,int);
void init(){
    for(int i=0;i<n;i++) dp[i][0]=a[i];
    for(int j=1;j<=log2(n);j++)
        for(int i=0;i+(1<<j)-1<n;i++)
            dp[i][j]=opt(dp[i][j-1],dp[i+(1<<(j-1))][j-1]);
}

查詢任意區間最值 $O(1)$

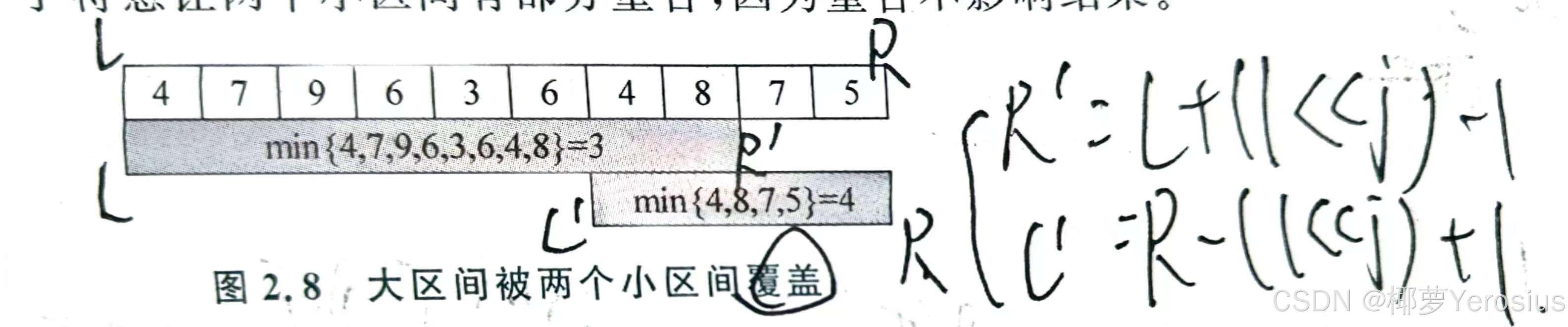
原理：設序列區間$[L,R]$，給定查詢區間$[l,r]$，區間長度為$len=r?l+1$。根據鴿巢原理，將查詢區間分為$[l,r^{\prime }]$和$[l^{\prime },r]$兩個等長小區間，其長度均為$x$($x\le len$且$2x\ge len$)，確保兩個小區間都能完全覆蓋，且對于$dp[][k]$，需確保$2^k=x$，$k={\log }_2(len)$，由此可知$r’=l+2^k?1$，$l^{\prime }=r?2^k+1$。

狀態轉移方程式：$RMQ(dp[l][k],dp[r?(1?k)+1][k])$

extern int dp[MAX][log2(n)+10],l2[n];
extern int l,r;
int opt(int,int);
int query(){
    int k=l2[r-l+1];
    return opt(dp[l][k],dp[r-(1<<k)+1][k]);
}