線段樹

模板題:線段樹1-洛谷(代碼)

線段樹是一種平衡二叉樹，其核心思想為二分+分治+懶標記，可在$O({\log }_{2}n)$的復雜度內完成單點修改、區間修改、區間查詢等操作。

設原序列長度為$n$，則每個節點$id(1\le id\le 4\times n)$都有一段原序列的管理區間$[L,R]$：

• 若$L=R$，則其為葉子節點，其管理區間長度為$1$，存儲即為原序列數據。$tree[id]=a[l]$；

• 若$L<R$，則為非葉子節點，其管理區間內存儲了該區間內的某種信息(如區間最值、區間GCD、區間和等)。每個節點$id$有兩個孩子，左孩子為$2\times id$，管理區間為$[L,M]$；右孩子為$2\times id+1$，管理區間為$[M+1,R]$，$M=\frac{L+R}{2}$。$tree[id]=opt(tree[2\times id],tree[2\times id+1])$。

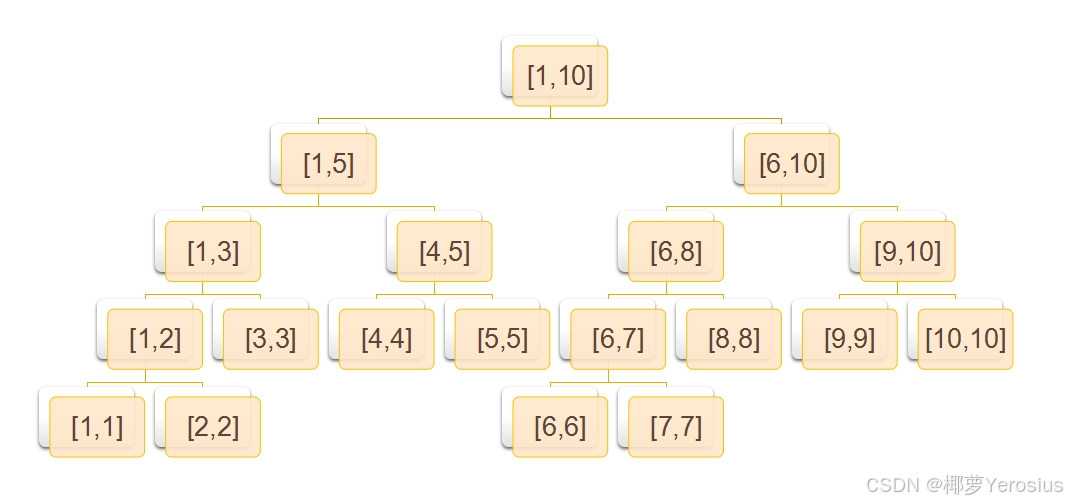
線段樹適用條件：大區間的值，可由若干個小區間的值合并而來。如可重復貢獻性問題、區間之和、區間之積等。

int n,v[n];
struct node{
    long long data,tag=0;//管理區間內的數據,懶標記標簽
}tree[n<<2];//線段樹數組開4*n
int opt(int a,int b);//具體操作函數

建樹

• 向下遞歸：先左后右，向下遞歸到葉子節點，向葉子節點中傳入原數組值
• 向上傳遞：葉子節點被傳入數據后，需組織成區間信息，并向其父節點傳遞(向上傳遞)

void pushup(int id){//向上傳遞
    tree[id].data=opt(tree[id<<1].data,tree[id<<1|1].data);
}
void build(int id,int l,int r){//id:當前遞歸節點 [l,r]:當前遞歸節點管理區間
    if(l==r) tree[id].data=a[l];//已遞歸到葉子節點
    else{
        int mid=l+r>>1;
        build(id<<1,l,mid);//先遞歸左孩子2*id,管理區間[l,mid]
        build(id<<1|1,mid+1,r);//然后遞歸到右孩子2*id+1,管理區間[mid+1,r]
        pushup(id);//向上傳遞
    }
}
//調用:build(1,1,n);

單點修改

設將$pos$處修改為$value$：

• 向下遞歸：遞歸至葉子節點找pos。若$pos\le mid$，則進入左孩子管理區間繼續遞歸；若$pos>mid$，則進入右孩子管理區間繼續遞歸
• 向上傳遞：修改后向上傳遞信息

void change(int id,int l,int r,int pos,int value){//當前遞歸節點及其管理區間
    if(l==r) tree[id].data=value,a[pos].data=value;//遞歸至葉子節點修改信息
    else{
        int mid=l+r>>1;
        if(pos<=mid) change(id<<1,l,mid);//若pos在[l,mid],進入左孩子管理區間
        else chage(id<<1|1,mid+1,r);//若pos在[mid+1,r],進入右孩子管理區間
        pushup(id);
    }
}

區間修改

關鍵操作：懶標記(Lazy Tag)。對每個節點定義區間標記$tag$，用于記錄其管理區間$[L,R]$內的統一修改，而對其中每個元素先不進行修改。僅當該管理區間元素的修改一致性被破壞時，才將自身$tag$向下傳遞給左右孩子，并清空自身$tag$。懶標記的作用就是等待下次向下傳遞時遞歸給左右孩子。

算法流程：設修改區間$[ml,mr]$，當前遞歸區間$[l,r]$：

• 若$[l,r]?[ml,mr]$(完全被修改區間覆蓋)，則直接將$[l,r]$打標記
• 否則無法被修改區間完全覆蓋，說明當前遞歸區間存在不應被修改的元素。向下對其左右子樹傳遞區間標記，并分別遞歸其左右子樹。

void addtag(int id,int l,int r,int d){//為節點打標記,此處以+d為例
    tree[id]+=d,tree[id]+=d*(r-l+1);
}
void pushdown(int id,int l,int r){//向下對左右孩子傳遞標記
    if(tree[id].tag){
        int mid=l+r>>1;
        addtag(id<<1,l,mid,tree[id].tag);
        addtag(id<<1|1,mid+1,r,tree[id].tag);
        tree[id].tag=0;
    }
}
void modify(int id,int l,int r,int ml,int mr,int d){//以區間[ml,mr]均+d為例
    if(ml<=l&&r<=mr){
        addtag(id,l,r,d);
    }else{
        pushdown(id,l,r);
        int mid=l+r>>1;
        if(ml<=mid) modify(id<<1,l,mid,ml,mr,d);
        if(mr>mid) modify(id<<1|1,mid+1,r,ml,mr,d);
        pushup(id);
    }
}

區間查詢

設查詢區間$[ql,qr]$，當前遞歸節點$id$管理區間為$[l,r]$：

• 若$[l,r]?[ql,qr]$：直接返回tree[id].data
• 若$[ql,qr]$與$[l,r]$部分重疊，則下傳懶標記，并分別遞歸其左右孩子

int query(int id,int l,int r,int ql,int qr){
    if(ql<=l&&r<=qr) return tree[id].data;
    pushdown(id,l,r);
    int mid=l+r>>1,ans ;//ans=0(區間之和) 1(區間之積) MAX/MAX+1(MAX/MIN)
    if(ql<=mid) ans=opt(ans,query(id<<1,l,mid,ql,qr));
    if(qr>mid) ans=opt(ans,query(id<<1|1,mid+1,r,ql,qr));
    return ans;
}