Splay學習筆記
Splay 學習筆記
前面的瞎BB
我很喜歡 Splay,雖然其中有一部分因素來源于對 Tarjan 老爺爺的崇拜(bushi
不過一想到 LCT 和 Splay 都是 Tarjan 和另外一位大佬發明的,就有種 Splay 為了 LCT 而生的錯覺(bushi
在學習之前建議先了解 BST 和平衡樹的概念當初我沒看這兩玩意直接沖Splay看得頭大
而且,我覺得如果你真的理解了 splay 這個操作,其實 Splay 寫起來是真的不要腦子,但是很多板子都有著相當多的亂七八糟的分類討論(讓我頭大)……
關于 Splay
其實 Splay 只有一個核心函數:旋轉到根。
rotate
先講一下旋轉。旋轉函數實質上就是將當前節點 \(p\) 的父親變為其兒子,同時此過程依舊要維護 BST 的性質。如下圖:
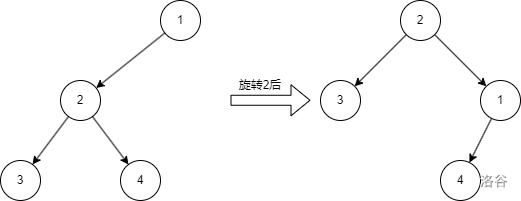
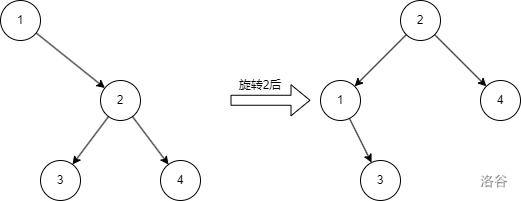
這種情況,我認為 旋轉 這個詞其實并不貼切,因為如果你用 旋轉 去形容它的話不那么直觀,我更愿意將其稱作 上移 ——將當前節點移到它的父親上面,同時滿足 BST 的性質。(但是旋轉念順口了啊喂qwq)
接下來我們做個分類討論:
-
如果當前節點(p)是其父親節點(fa)的左兒子:
為了保證 BST 的性質,那么在旋轉過后 fa 將變成 p 的右兒子,而 p 原本的右兒子將會變成 fa 的左兒子。 -
如果當前節點(p)是其父親節點(fa)的右兒子:
那么旋轉過后 fa 將會變成 p 的左兒子,而 p 原本的左兒子將會變成 fa 的右兒子。
此處建議大家手玩一下這個旋轉操作,就會發現,所謂的 旋轉,其實本質上就是將當前節點 p 上移以后重新處理和其兒子、父親的連邊。
指針實現:
struct node {
node *son[2], *fa;
};
// 對于一個節點 *p, p->son[0] 為它的左兒子,p->son[1] 為它的右兒子
int get(node *p) {
if (p->fa->son[0] == p) return 0;
return 1;
}
// 可簡寫成: return p->fa->son[1] == son;
// 將 fa 和 son 重新連邊,并且 son 是 fa 的左/右子樹
void connect(node *fa, node *son, int d) {
if (fa != nullptr) fa->son[d] = son;
if (son != nullptr) son->fa = fa;
}
// 重新維護 p,這個重新維護其實和線段樹里的 pushup 本質上是一樣的
void maintain(node *p) {
if (p == nullptr) return;
// ...
}
void rotate(node *p) {
node *fa = p->fa, *grand = fa->fa;
int d = get(p), fd = get(fa);
connect(fa, p->son[d ^ 1], d); // p 的 d ^ 1 兒子將會變成 fa,所以這個兒子必須被 fa 所管理
connect(p, fa, d ^ 1); // fa會變成 p 的與 d 剛好相反的兒子
connect(grand, p, fd); // 無論 p 和 fa 怎么玩,它們相對 grand 的子樹將始終不變
// 在一次旋轉過程中,將會影響三個節點:fa,p,grand
// 同時在旋轉之后從下往上的順序也是fa, p, grand,所以維護先后順序也要注意。
maintain(fa), maintain(p), maintain(grand);
}
數組實現:
const int kMaxN = 1e6;
struct node {
int son[2], fa;
}a[kMaxN];
int get(int p) {
return a[a[p].fa].son[1] == p;
}
void connect(int fa, int son, int d) {
if (fa) a[fa].son[d] = son;
if (son) a[son].fa = fa;
}
void maintain(int p) {
// ...
}
void rotate(int p) {
itn fa = a[p].fa, grand = a[fa].fa;
int d = get(p), fd = get(fa);
connect(fa, a[p].son[d ^ 1], d);
connect(p, fa, d ^ 1);
connect(gradn, p, fd);
maintain(fa), maintain(p), maintain(grand);
}
這份代碼中 rotate 用 connect 避免了對空指針的特殊考慮,將空指針的特殊情況由 connect 統一管理。這么寫會讓代碼更加直觀一些。
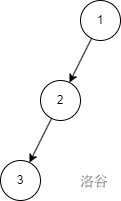
等會啊,rotate 有個啥用呢?它也不能保證旋轉某個節點后樹一定是平衡的啊。如下圖(節點旁數字代表高度):
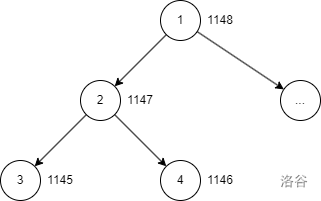
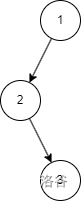
這本來是一個很平衡的狀態,然后我們輕輕地將 2 旋轉一下:
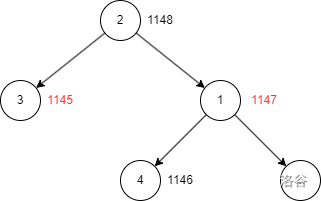
完犢子嘞!以 2 為根的兩個子樹并不能保證平衡。也就是說,你可以通過各種稀奇古怪的操作使兩個子樹的高度差越來越大、越來越大……最后甚至可能退化成一個鏈(當然也許沒這么恐怖但是大差不差了)
如果我們不進行場景而直接使用旋轉亂搞的話,很容易導致 BST 不再平衡然后被各種毒瘤出題人卡飛
splay
Splay 獨有的伸展操作/splay操作就是為了解決這個問題而誕生的。
首先 splay 強制要求你每次訪問一個節點之后要將其旋轉至根節點。沒事也就只是多個常數而已(所以Splay常數大XD)。同時在 Splay 操作中維護 p 到根節點上的點使其能夠保持平衡。
首先分三種情況討論:
- 父親節點就是根節點。沒什么好說的直接移就完事。
- 當前節點、父親節點、祖先節點共線:
![]()
這種情況下,先旋轉父親節點再旋轉當前節點。 - 當前節點、父親節點、祖先節點不共線:
![]()
這種情況下,直接旋轉兩遍當前節點。
啊,你問我為啥這樣子整體會更平衡?
巧了我也不會證,但是oi-wiki上有
但是不可否認的是它確實將時間復雜度壓了下來,并且均攤成了 \(\log n\)
指針實現:
void splay(node *p) {
while (1) {
if (p->fa == root) {
rotate(p);
break;
}
if (get(p->fa) == get(p)) {
rotate(p->fa);
rotate(p);
} else {
rotate(p);
rotate(p);
}
}
root = p;
}
數組實現:
void splay(int p) {
while (1) {
if (a[p].fa == root) {
rotate(p);
break;
}
if (get(a[p].fa) == get(p)) {
rotate(a[p].fa);
rotate(p);
} else {
rotate(p);
rotate(p);
}
}
}
看上去很難看,有一個更簡潔的寫法:
指針實現:
void splay(node *p) {
for (node *fa; (fa = p->fa) != nullptr; rotate(p)) {
if (fa->fa != nullptr) {
rotate(get(p) == get(fa) ? fa : p);
}
}
root = p;
}
數組實現:
void splay(int p) {
for (int fa; (fa = a[p].fa) != 0; rotate(p)) {
if (a[fa].fa != 0) {
rotate(get(p) == get(fa) ? fa : p);
}
}
root = p;
}
很顯然,根節點是沒有父親的。如果一個節點沒有父親,那么我便可以認為它已經成為了根節點。
基于這個思路,我們還可以將 splay 操作拓展理解為:將某個節點不斷旋轉,直到它的父親成為了另外一個節點。如果它的父親指針為空,那么等價于它會移到根節點。
指針實現:
void splay(node *p, node *top) {
for (node *fa; (fa = p->fa) != top; rotate(p)) {
if (fa->fa != top) {
rotate(get(p) == get(fa) ? fa : p);
}
}
if (top == nullptr) root = p;
}
數組實現:
void splay(int p, int top) {
for (int fa; (fa = p->fa) != top; rotate(p)) {
if (a[fa].fa != top) {
rotate(get(p) == get(fa) ? fa : p);
}
}
if (top == 0) root = p;
}
一些代碼細節
哨兵節點
燒餅節點
哨兵節點僅僅只是一種占位節點。它通常表示為無窮大或者無窮小。
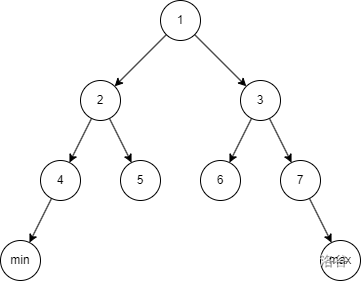
在上圖,我們設定了兩個哨兵節點代表無窮大和無窮小。我們并不關系它們是否有具體取值,但是在 BST 中它的鍵值就是無窮大和無窮小。
可以根據情況來選擇寫一個或兩個哨兵節點。但是無論如何,哨兵節點是一定要寫的,這樣可以減少許多的分類討論(如插入節點是不需要再判斷樹是否為空)。
用一個節點代替空指針
如果你是用數組實現的 Splay,那么這里可以跳過。
如果你用指針寫,那么多少會遇到在 maintain 等環節需要考慮子樹是否為空的苦惱,當訪問到空指針也確實是一件比較難調的事情。
我們可以自己定義一個指針 nil,在默認情況下它將是所有節點的兒子節點、父親節點:
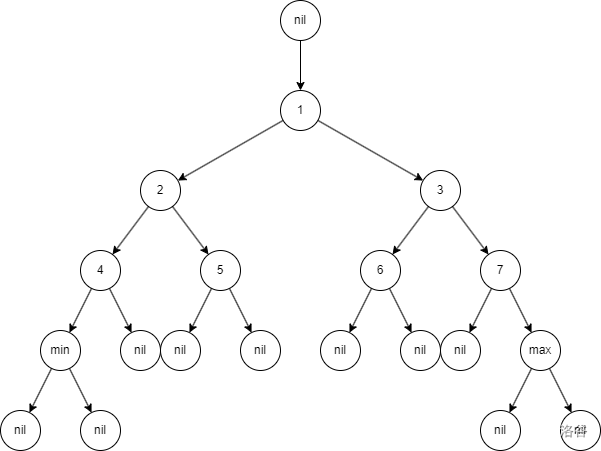
nil 自己的左右兒子和父親將永遠是自己,它不會指向其它節點只有其它節點會指向它。
nil 不是必須的,它的唯一作用就是代替空指針,并且可以為它賦上一定的值,這樣講減少很多情況下針對空指針的分類討論。
具體操作
kth、查詢前驅后繼
BST 的基礎操作,自己去搞。
不過記得找到之后把它 splay 到根
插入
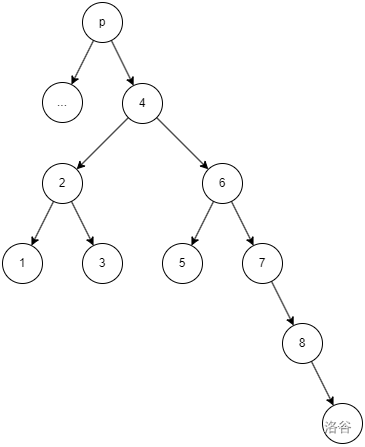
假如我要往節點 p 后插入一個節點。
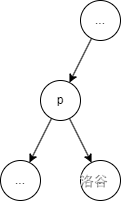
先把 p 旋轉到根
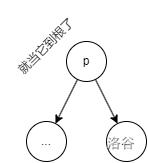
然后直接插入就完事了
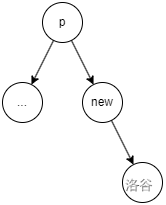
p 原本的右子樹就接到 new 上面去了。
插入序列/Splay合并
如果我們要往 p 后插入一個序列,和上面插入節點操作一樣,先將 p 旋轉到根,然后把需要插入的序列構造成一個平衡樹。
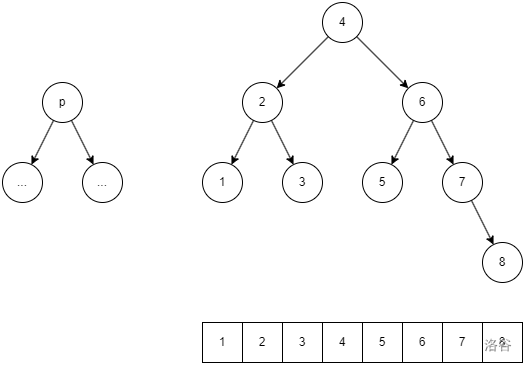
有兩個插入的方法:
-
直接插入:
![]()
操作完之后最好再把 8 號節點 splay 一遍,這樣可以維護好它到根節點所有節點的信息。 -
查詢后繼后插入:
這么做有一個問題:如果我沒有后繼怎么?所以上文中提到了無窮大的哨兵節點就是這么用的,它保證了一定會有后繼。
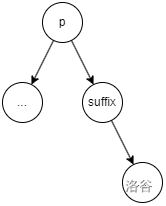
首先將 p 的后繼直接旋轉到 p 下面來。
![]()
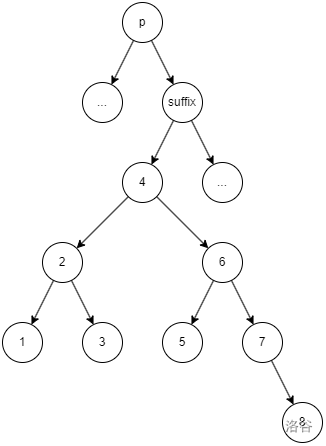
suffix 是一定沒有左子樹的,基于 BST 的性質,接下來可以直接把要插入的序列插入進去
![]()
維護好 suffix 和 p 的信息就完了。
基于這個思路,若Splay維護的序列上的信息你也可以用這種方式快速合并(不過要把哨兵節點去掉)
當然,如果你是將兩個按照鍵值排序的Splay合并……老老實實寫啟發式合并吧。
操作連續子序列/Splay分裂
其實Splay也是可以處理分裂的,只是不用分裂合并維護平衡罷了。
如果我們想要操作一個區間,一個合理的方式是將這個區間內的節點全部獨立到一顆子樹里,如下圖:
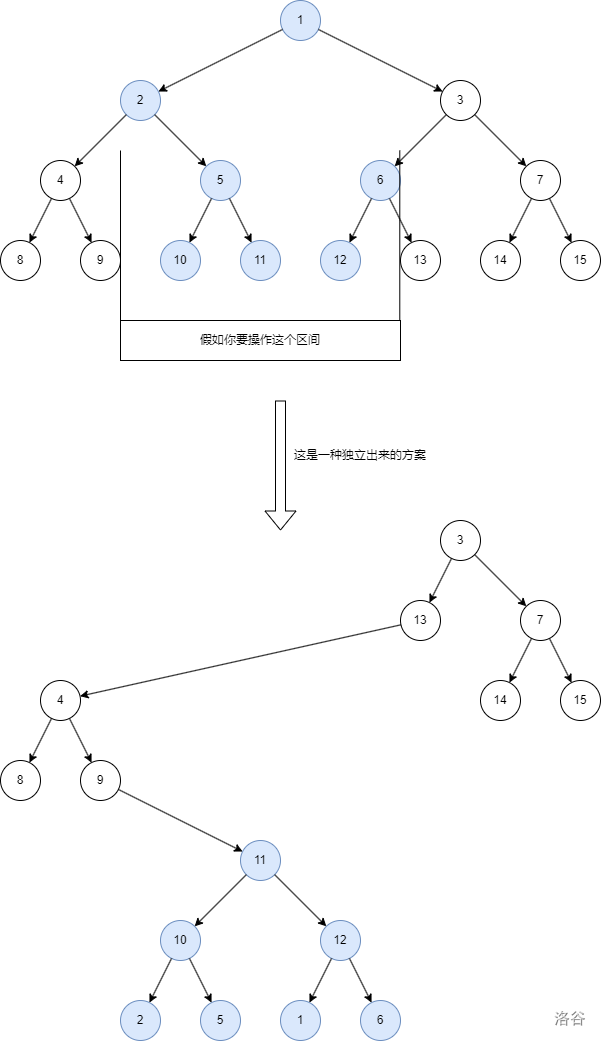
雖然看上去并不好看,但是確實達成了我們的要求。將我們需要操作的節點都獨立到了一個子樹里。這樣我們做區間修改還是區間查詢時,只需要對這個子樹的根節點進行操作就可以了。
假設我們要獨立一個區間 l, r,那么只需要把 l - 1 和 r + 1 (下面稱呼為前驅和后繼)的節點通過 splay 操作向上旋轉即可。我常做的方法是將前驅旋轉至根、將后繼旋轉至前驅下,如下圖:
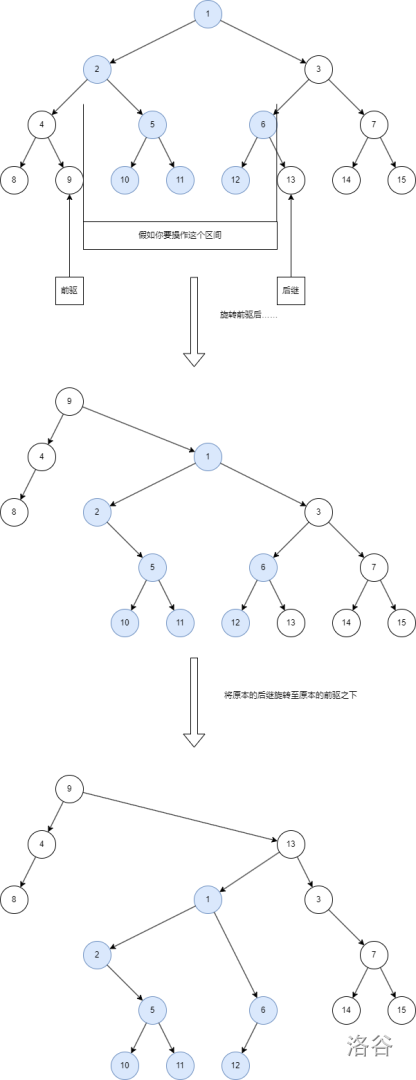
由于我們并不會破壞 BST 的性質,旋轉后的后繼的左子樹,一定是 l, r 對應的子樹。
也許你會有疑問:第一個節點沒有前驅、最后一個點沒有后繼。如果你使用了哨兵節點來代表無窮小和無窮大,這個問題就可以避免,減少分類討論的必要。
利用將子樹獨立出來的方式,可以將一個 Splay 分裂成兩個 Splay,具體實現應該很顯然。
刪除
依舊用上面的樹為例子:
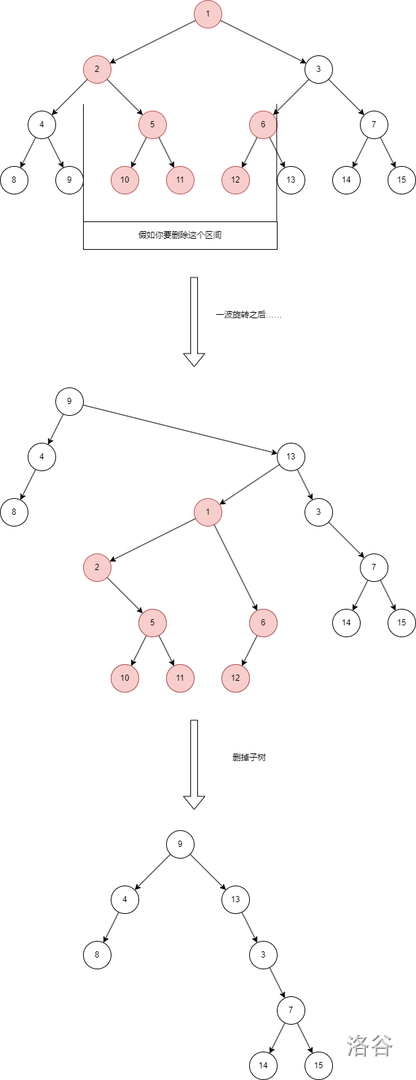
直接將要刪除的區間獨立出來,然后可以方便刪除。
板子
這里只給出了最基礎最基礎的板子,沒有任何實際功能。
class Splay {
struct node {
node *son[2] = {nullptr, nullptr}, *fa = nullptr;
} *root;
int get(node *p) {
return p->fa->son[1] == p;
}
void connect(node *fa, node *son, int d) {
if (fa != nullptr) fa->son[d] = son;
if (son != nullptr) son->fa = fa;
}
void maintain(node *p) {}
void rotate(node *p) {
int d = get(p), fd = get(p->fa);
node *fa = p->fa, *grand = fa->fa;
connect(p->fa, p->son[d ^ 1], d);
connect(p, fa, d ^ 1);
connect(grand, p, fd);
maintain(fa), maintain(p), maintain(grand);
}
void splay(node *p, node *top = nullptr) {
for (node *fa; (fa = p->fa) != top; rotate(p)) {
if (fa->fa != top) rotate(get(p) == get(fa) ? fa : p);
}
if (top == nullptr) root = p;
}
public:
};
數組實現:
你問這個啊?懶得寫了自己寫去吧qwq
我覺得我寫的還是挺詳細的,然后所有的內容自己去補充吧……



 浙公網安備 33010602011771號
浙公網安備 33010602011771號