思維導圖

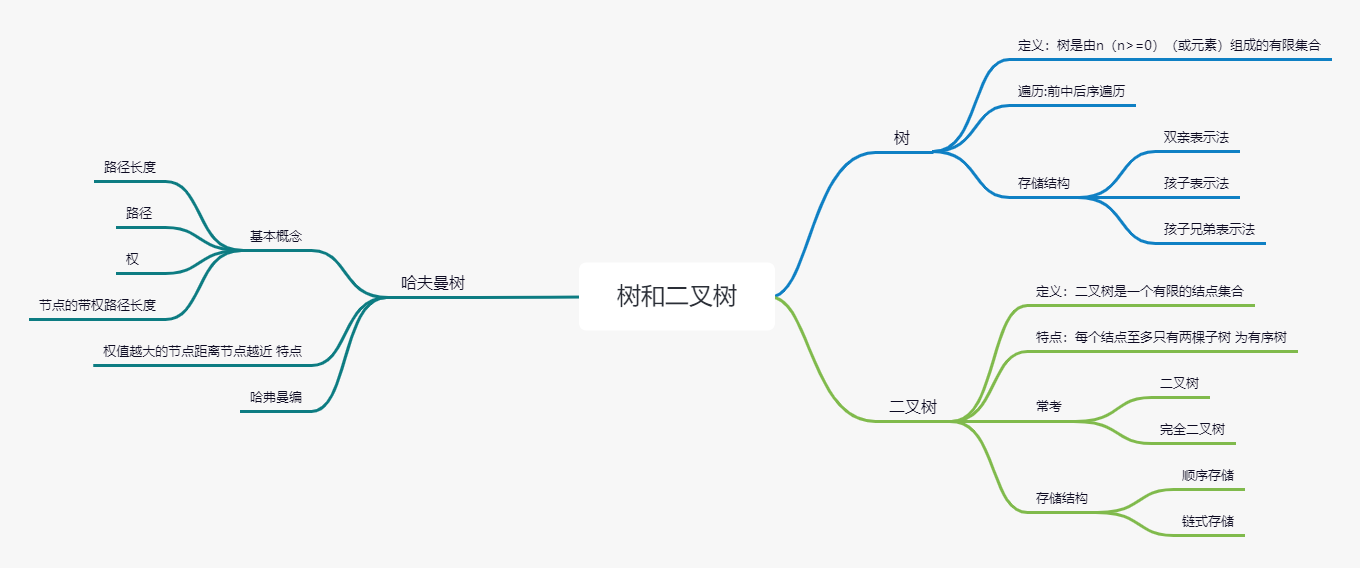
樹
基本概念 ：樹是一種非線性結構，常用于表示有層次關系的數據。樹有多種邏輯表達方式，常用的有樹形、文氏圖、凹入、括號表示法。
樹的基本術語
（1）結點的度與樹的度：結點的度是樹中某個結點的的子樹的個數；樹的度是樹中所以結點的度中的最大值為（將度為m的樹叫做m次樹）
（2）分支結點與葉子結點：分支結點是度不為零的結點；葉子結點是度為零的結點
（3)孩子結點、雙親結點、兄弟結點：孩子結點就是一棵樹中每一個結點的后繼結點 顧名思義可以知道雙親結點、兄弟結點、子孫結點，祖先結點
（5）結點的層次和樹的高度：結點層次就是從樹根開始，樹根為第一層接著其孩子結點為其第二層以此類推；樹中結點的最大層次就是書的高度
（6）有序樹無序樹：樹中各個結點的子樹是按照一定的次序從左向右安排，次序不能隨意變換這就是有序樹；否則就是無序樹
（7）森林：n個互不相交的樹的集合
樹的性質：
（1）樹中的結點樹等于所以結點的度數之和加一
（2）度為m的樹中第i層上最多有m的i減一次方個結點
樹的基本運算：
（1）先根遍歷
（1）中根遍歷
（1）后根遍歷
二叉樹
基本概念：二叉樹是n (n≥0)個結點的有限集合，或者為空二叉樹,即n= 0或者由一個根結點和兩個互不相交的被稱為根的左子樹和右子樹組成，左子樹和右子樹又分別是—棵二叉樹。
二叉樹的性質：
（1）設非空二叉樹中度為0、1和2的結點個數分別為n0、n1和n2，則n0 = n2+ 1(葉子結點比二分支結點多—個)
（2）二叉樹第i層至多有2^(i-1)個結點(i≥1)
（3）m叉樹第i層至多有m^(i-1)個結點(≥1)
（4）高度為h的二叉樹至多有2-1個結點(滿二叉樹)
（5）高度為h的m叉樹至多有(mh-1)/(m-1)個結點
完全二叉樹：當且僅當其每個結點都與高度為h的滿二叉樹中編號為1~n的結點一一對應時，稱為完全二叉樹。完全二叉樹只有最后兩層可能有葉子結點，最多只有—個度為1的結點，按層序從1開始編號，結點i的左孩了為2i，右孩子為Zi+1;結點i的父節點為i12(如果有的話)is _n12」為分支結點,i>n12j為葉子結點
存儲結構：
（1）順序結構：定義一個長度為MaxSize的數組t，按照從上至下、從左至右的順序依次存儲完全二叉樹中的各個結點；最壞情況：高度為h且只有h個結點的單支樹(所有結點只有右孩子)，也至少需要2個h-1個存儲單元（二叉樹的順序存儲結構，只適合存儲完全二叉樹）
（2）鏈式結構：n個結點的二叉鏈表共有n+1個空鏈域
哈夫曼樹：
定義：在n個帶權葉子結點構成的所以二叉樹中，帶權路徑長度WPL最小的二叉樹稱為哈夫曼樹（采用順序存儲結構）
基本概念：
（1）路徑:兩個結點之間路過的分支
（2）結點的路徑長度:路徑上的分支數
（3）樹的路徑長度:從樹根到每一個結點的路徑長度
（4）結點數目相同的二叉樹，完全二叉樹路徑長度最之和。記作TL。
（5）權︰將樹中結點賦給一個有著某種含義的數值，則這個數值成為該結點的權
（6）結點的帶權路徑長度:從根結點到該結點之間的路徑長度與該結點權的乘積
（7）樹的帶權路徑長度:樹的所有葉子結點的帶權路徑長度之和。記作WPL
哈夫曼樹以及應用：
1.構造哈夫曼樹
貪心算法:首先選擇權值較小的葉子
2.哈夫曼算法:
（1）構造森林全是根
（2）選用兩小造新樹
（3）刪除兩小添新人
（4）重復2、3剩單根
3.合并n-1次，產生n-1個新結點